เริ่มต้นใช้งาน TensorFlow: บทช่วยสอนการเรียนรู้ของเครื่อง
เผยแพร่แล้ว: 2022-03-11TensorFlow เป็นไลบรารีซอฟต์แวร์โอเพ่นซอร์สที่สร้างโดย Google ซึ่งใช้เพื่อนำการเรียนรู้ของเครื่องและระบบการเรียนรู้เชิงลึกมาใช้ ชื่อทั้งสองนี้มีชุดของอัลกอริธึมที่ทรงพลังซึ่งมีความท้าทายร่วมกัน—เพื่อให้คอมพิวเตอร์เรียนรู้วิธีระบุรูปแบบที่ซับซ้อนโดยอัตโนมัติและ/หรือเพื่อการตัดสินใจที่ดีที่สุด
หากคุณสนใจรายละเอียดเกี่ยวกับระบบเหล่านี้ คุณสามารถเรียนรู้เพิ่มเติมจากบล็อกโพสต์ Toptal เกี่ยวกับการเรียนรู้ของเครื่องและการเรียนรู้เชิงลึก
หัวใจของ TensorFlow คือห้องสมุดสำหรับการเขียนโปรแกรมกระแสข้อมูล ใช้ประโยชน์จากเทคนิคการเพิ่มประสิทธิภาพต่างๆ เพื่อให้การคำนวณนิพจน์ทางคณิตศาสตร์ง่ายขึ้นและมีประสิทธิภาพมากขึ้น
คุณสมบัติที่สำคัญบางประการของ TensorFlow คือ:
- ทำงานอย่างมีประสิทธิภาพด้วยนิพจน์ทางคณิตศาสตร์ที่เกี่ยวข้องกับอาร์เรย์หลายมิติ
- การสนับสนุนที่ดีของโครงข่ายประสาทเทียมระดับลึกและแนวคิดการเรียนรู้ของเครื่อง
- การประมวลผล GPU/CPU ที่สามารถเรียกใช้โค้ดเดียวกันบนสถาปัตยกรรมทั้งสองได้
- ความสามารถในการคำนวณในระดับสูงระหว่างเครื่องจักรและชุดข้อมูลขนาดใหญ่
คุณสมบัติเหล่านี้ร่วมกันทำให้ TensorFlow เป็นเฟรมเวิร์กที่สมบูรณ์แบบสำหรับระบบอัจฉริยะในระดับการผลิต
ในบทช่วยสอน TensorFlow นี้ คุณจะได้เรียนรู้วิธีที่คุณสามารถใช้วิธีการแมชชีนเลิร์นนิงที่เรียบง่ายแต่ทรงพลังใน TensorFlow และวิธีที่คุณสามารถใช้ไลบรารีเสริมเพื่อดีบั๊ก แสดงภาพ และปรับแต่งโมเดลที่สร้างขึ้นด้วย
การติดตั้ง TensorFlow
เราจะใช้ TensorFlow Python API ซึ่งใช้งานได้กับ Python 2.7 และ Python 3.3+ รุ่น GPU (Linux เท่านั้น) ต้องใช้ Cuda Toolkit 7.0+ และ cuDNN v2+
เราจะใช้ระบบการจัดการการพึ่งพาแพ็คเกจ Conda เพื่อติดตั้ง TensorFlow Conda ช่วยให้เราสามารถแยกสภาพแวดล้อมต่างๆ ออกจากเครื่องได้ คุณสามารถเรียนรู้วิธีติดตั้ง Conda ได้จากที่นี่
หลังจากติดตั้ง Conda เราสามารถสร้างสภาพแวดล้อมที่เราจะใช้สำหรับการติดตั้งและใช้งาน TensorFlow คำสั่งต่อไปนี้จะสร้างสภาพแวดล้อมของเราพร้อมกับไลบรารีเพิ่มเติม เช่น NumPy ซึ่งมีประโยชน์มากเมื่อเราเริ่มใช้ TensorFlow
เวอร์ชัน Python ที่ติดตั้งในสภาพแวดล้อมนี้คือ 2.7 และเราจะใช้เวอร์ชันนี้ในบทความนี้
conda create --name TensorflowEnv biopython เพื่อให้ง่ายขึ้น เรากำลังติดตั้ง biopython ที่นี่ แทนที่จะติดตั้งแค่ NumPy ซึ่งรวมถึง NumPy และแพ็คเกจอื่นๆ ที่เราจำเป็นต้องใช้ คุณสามารถติดตั้งแพ็คเกจได้ตามต้องการโดยใช้ conda install หรือคำสั่ง pip install
คำสั่งต่อไปนี้จะเปิดใช้งานสภาพแวดล้อม Conda ที่สร้างขึ้น เราจะสามารถใช้แพ็คเกจที่ติดตั้งภายในนั้นได้ โดยไม่ต้องผสมกับแพ็คเกจที่ติดตั้งทั่วโลกหรือในสภาพแวดล้อมอื่นๆ
source activate TensorFlowEnvเครื่องมือติดตั้ง pip เป็นส่วนมาตรฐานของสภาพแวดล้อม Conda เราจะใช้มันเพื่อติดตั้งไลบรารี TensorFlow ก่อนที่จะทำเช่นนั้น ขั้นตอนแรกที่ดีคือการอัพเดต pip เป็นเวอร์ชันล่าสุด โดยใช้คำสั่งต่อไปนี้:
pip install --upgrade pipตอนนี้เราพร้อมที่จะติดตั้ง TensorFlow โดยเรียกใช้:
pip install tensorflowการดาวน์โหลดและสร้าง TensorFlow อาจใช้เวลาหลายนาที ในขณะที่เขียน สิ่งนี้จะติดตั้ง TensorFlow 1.1.0
กราฟการไหลของข้อมูล
ใน TensorFlow การคำนวณอธิบายโดยใช้กราฟการไหลของข้อมูล แต่ละโหนดของกราฟแสดงถึงอินสแตนซ์ของการดำเนินการทางคณิตศาสตร์ (เช่น การบวก การหาร หรือการคูณ) และแต่ละขอบคือชุดข้อมูลหลายมิติ (เทนเซอร์) ที่ใช้ดำเนินการ
เนื่องจาก TensorFlow ทำงานร่วมกับกราฟการคำนวณ กราฟเหล่านี้จะได้รับการจัดการโดยที่แต่ละโหนดแสดงถึงอินสแตนซ์ของการดำเนินการ โดยที่การดำเนินการแต่ละรายการมีอินพุตเป็นศูนย์หรือมากกว่า และมีเอาต์พุตเป็นศูนย์หรือมากกว่า
ขอบใน TensorFlow สามารถจัดกลุ่มได้เป็นสองประเภท: โครงสร้างข้อมูลการถ่ายโอนขอบปกติ (เทนเซอร์) ซึ่งเป็นไปได้ที่เอาต์พุตของการดำเนินการหนึ่งจะกลายเป็นอินพุตสำหรับการดำเนินการอื่นและขอบพิเศษซึ่งใช้เพื่อควบคุมการพึ่งพาระหว่างสองโหนดเพื่อตั้งค่า ลำดับการทำงานโดยที่โหนดหนึ่งรอให้โหนดอื่นเสร็จสิ้น
นิพจน์ง่ายๆ
ก่อนที่เราจะพูดถึงองค์ประกอบต่างๆ ของ TensorFlow ก่อนอื่นเราจะทำเซสชั่นการทำงานกับ TensorFlow เพื่อให้เข้าใจถึงลักษณะของโปรแกรม TensorFlow
เริ่มต้นด้วยนิพจน์ง่ายๆ และสมมติว่า ด้วยเหตุผลบางอย่าง เราต้องการประเมินฟังก์ชัน y = 5*x + 13 ในรูปแบบ TensorFlow
ในโค้ด Python อย่างง่ายจะมีลักษณะดังนี้:
x = -2.0 y = 5*x + 13 print yซึ่งให้ผลลัพธ์แก่เราในกรณีนี้ 3.0
ตอนนี้เราจะแปลงนิพจน์ด้านบนเป็นเงื่อนไข TensorFlow
ค่าคงที่
ใน TensorFlow ค่าคงที่จะถูกสร้างขึ้นโดยใช้ค่าคงที่ของฟังก์ชัน ซึ่งมี constant(value, dtype=None, shape=None, name='Const', verify_shape=False) โดยที่ value เป็นค่าคงที่จริงที่จะนำไปใช้ การคำนวณเพิ่มเติม dtype เป็นพารามิเตอร์ประเภทข้อมูล (เช่น float32/64, int8/16 เป็นต้น) shape เป็นมิติทางเลือก name เป็นชื่อทางเลือกสำหรับเทนเซอร์ และพารามิเตอร์สุดท้ายคือบูลีนซึ่งระบุถึงการตรวจสอบความถูกต้องของ รูปร่างของค่า
หากคุณต้องการค่าคงที่ที่มีค่าเฉพาะภายในโมเดลการฝึกของคุณ คุณสามารถใช้อ็อบเจกต์ constant ที่ได้ดังตัวอย่างต่อไปนี้:
z = tf.constant(5.2, name="x", dtype=tf.float32)ตัวแปร
ตัวแปรใน TensorFlow คือบัฟเฟอร์ในหน่วยความจำที่มีเทนเซอร์ซึ่งต้องได้รับการเตรียมใช้งานอย่างชัดเจนและใช้ในกราฟเพื่อรักษาสถานะตลอดเซสชัน โดยเพียงแค่เรียกตัวสร้างตัวแปรจะถูกเพิ่มในกราฟการคำนวณ
ตัวแปรมีประโยชน์อย่างยิ่งเมื่อคุณเริ่มต้นด้วยโมเดลการฝึก และใช้เพื่อเก็บและอัปเดตพารามิเตอร์ ค่าเริ่มต้นที่ส่งผ่านเป็นอาร์กิวเมนต์ของคอนสตรัคเตอร์แสดงถึงเทนเซอร์หรือออบเจกต์ซึ่งสามารถแปลงหรือส่งคืนเป็นเทนเซอร์ได้ นั่นหมายความว่า หากเราต้องการเติมตัวแปรด้วยค่าที่กำหนดไว้ล่วงหน้าหรือค่าสุ่มบางค่าเพื่อใช้ในภายหลังในกระบวนการฝึกอบรมและอัปเดตผ่านการวนซ้ำ เราสามารถกำหนดได้ดังนี้:
k = tf.Variable(tf.zeros([1]), name="k")อีกวิธีหนึ่งในการใช้ตัวแปรใน TensorFlow คือการคำนวณโดยที่ตัวแปรนั้นไม่สามารถฝึกได้ และสามารถกำหนดได้ดังนี้:
k = tf.Variable(tf.add(a, b), trainable=False)เซสชั่น
ในการประเมินโหนดจริง ๆ เราต้องเรียกใช้กราฟการคำนวณภายในเซสชัน
เซสชันสรุปการควบคุมและสถานะของรันไทม์ TensorFlow เซสชันที่ไม่มีพารามิเตอร์จะใช้กราฟเริ่มต้นที่สร้างในเซสชันปัจจุบัน มิฉะนั้นคลาสเซสชันจะยอมรับพารามิเตอร์กราฟ ซึ่งใช้ในเซสชันนั้นที่จะดำเนินการ
ด้านล่างนี้คือข้อมูลโค้ดสั้นๆ ที่แสดงให้เห็นว่าคำศัพท์ที่กำหนดไว้ด้านบนนี้สามารถนำมาใช้ใน TensorFlow เพื่อคำนวณฟังก์ชันเชิงเส้นอย่างง่ายได้อย่างไร
import tensorflow as tf x = tf.constant(-2.0, name="x", dtype=tf.float32) a = tf.constant(5.0, name="a", dtype=tf.float32) b = tf.constant(13.0, name="b", dtype=tf.float32) y = tf.Variable(tf.add(tf.multiply(a, x), b)) init = tf.global_variables_initializer() with tf.Session() as session: session.run(init) print session.run(y)การใช้ TensorFlow: การกำหนดกราฟการคำนวณ
ข้อดีของการทำงานกับกราฟโฟลว์ข้อมูลคือโมเดลการดำเนินการแยกออกจากการดำเนินการ (บน CPU, GPU หรือชุดค่าผสมบางส่วน) ซึ่งเมื่อใช้งานแล้ว ซอฟต์แวร์ใน TensorFlow สามารถใช้กับ CPU หรือ GPU ที่ความซับซ้อนทั้งหมดที่เกี่ยวข้องกับโค้ด การดำเนินการถูกซ่อนไว้
กราฟการคำนวณสามารถสร้างขึ้นในกระบวนการของการใช้ไลบรารี TensorFlow โดยไม่ต้องสร้างอินสแตนซ์ของวัตถุกราฟอย่างชัดเจน
วัตถุกราฟใน TensorFlow สามารถสร้างได้โดยใช้บรรทัดของโค้ดอย่างง่าย เช่น c = tf.add(a, b) สิ่งนี้จะสร้างโหนดการทำงานที่ใช้เมตริกซ์สอง a และ b ที่สร้างผลรวม c เป็นเอาต์พุต
กราฟการคำนวณเป็นกระบวนการในตัวที่ใช้ไลบรารีโดยไม่จำเป็นต้องเรียกวัตถุกราฟโดยตรง ออบเจ็กต์กราฟใน TensorFlow ซึ่งประกอบด้วยชุดของการดำเนินการและเทนเซอร์เป็นหน่วยของข้อมูล ถูกใช้ระหว่างการดำเนินการที่ยอมให้มีกระบวนการเดียวกัน และมีกราฟมากกว่าหนึ่งกราฟ โดยที่แต่ละกราฟจะถูกกำหนดให้กับเซสชันที่ต่างกัน ตัวอย่างเช่น บรรทัดอย่างง่ายของโค้ด c = tf.add(a, b) จะสร้างโหนดการทำงานที่รับเมตริกซ์ a และ b สองตัวเป็นอินพุต และสร้างผลรวมของ c เป็นเอาต์พุต
TensorFlow ยังจัดเตรียมกลไกการป้อนสำหรับการแพตช์เทนเซอร์กับการดำเนินการใดๆ ในกราฟ โดยที่ฟีดจะแทนที่เอาต์พุตของการดำเนินการด้วยค่าเทนเซอร์ ข้อมูลฟีดจะถูกส่งเป็นอาร์กิวเมนต์ในการเรียกใช้ฟังก์ชัน run()
ตัวยึดตำแหน่งเป็นวิธีของ TensorFlow ในการอนุญาตให้นักพัฒนาแทรกข้อมูลลงในกราฟการคำนวณผ่านตัวยึดตำแหน่งซึ่งถูกผูกไว้ภายในนิพจน์บางรายการ ลายเซ็นของตัวยึดตำแหน่งคือ:
placeholder(dtype, shape=None, name=None)โดยที่ dtype เป็นประเภทขององค์ประกอบในเทนเซอร์และสามารถให้ทั้งรูปร่างของเทนเซอร์ที่จะป้อนและชื่อสำหรับการดำเนินการ
หากไม่ผ่านรูปร่าง เทนเซอร์นี้สามารถป้อนด้วยรูปร่างใดก็ได้ หมายเหตุสำคัญคือ ตัวยึดตำแหน่งจะต้องถูกป้อนด้วยข้อมูล มิฉะนั้น เมื่อดำเนินการเซสชั่นและหากส่วนนั้นหายไป ตัวยึดตำแหน่งจะสร้างข้อผิดพลาดด้วยโครงสร้างต่อไปนี้:
InvalidArgumentError (see above for traceback): You must feed a value for placeholder tensor 'y' with dtype floatข้อดีของตัวยึดตำแหน่งคืออนุญาตให้นักพัฒนาสร้างการดำเนินการ และกราฟการคำนวณโดยทั่วไป โดยไม่ต้องให้ข้อมูลล่วงหน้าสำหรับสิ่งนั้น และสามารถเพิ่มข้อมูลจากแหล่งภายนอกในรันไทม์ได้
ลองใช้ปัญหาง่ายๆ ในการคูณจำนวนเต็ม x และ y สองจำนวนในแบบ TensorFlow โดยที่ตัวยึดตำแหน่งจะถูกใช้ร่วมกับกลไกฟีดผ่านเมธอดการ run เซสชัน
import tensorflow as tf x = tf.placeholder(tf.float32, name="x") y = tf.placeholder(tf.float32, name="y") z = tf.multiply(x, y, name="z") with tf.Session() as session: print session.run(z, feed_dict={x: 2.1, y: 3.0})การแสดงภาพกราฟการคำนวณด้วย TensorBoard
TensorBoard เป็นเครื่องมือสร้างภาพสำหรับวิเคราะห์กราฟการไหลของข้อมูล ซึ่งจะเป็นประโยชน์ในการทำความเข้าใจโมเดลการเรียนรู้ของเครื่องให้ดีขึ้น
ด้วย TensorBoard คุณจะได้รับข้อมูลเชิงลึกเกี่ยวกับสถิติประเภทต่างๆ เกี่ยวกับพารามิเตอร์และรายละเอียดเกี่ยวกับส่วนต่างๆ ของกราฟการคำนวณโดยทั่วไป ไม่ใช่เรื่องแปลกที่โครงข่ายประสาทเทียมลึกมีโหนดจำนวนมาก TensorBoard ช่วยให้นักพัฒนาได้รับข้อมูลเชิงลึกในแต่ละโหนดและวิธีดำเนินการคำนวณบนรันไทม์ TensorFlow
ตอนนี้ กลับมาที่ตัวอย่างของเราตั้งแต่ต้นบทช่วยสอน TensorFlow ที่เรากำหนดฟังก์ชันเชิงเส้นด้วยรูปแบบ y = a*x + b
เพื่อบันทึกเหตุการณ์จากเซสชันซึ่งภายหลังสามารถใช้ใน TensorBoard ได้ TensorFlow ได้จัดเตรียมคลาส FileWriter สามารถใช้เพื่อสร้างไฟล์เหตุการณ์สำหรับเก็บบทสรุปโดยที่ Constructor ยอมรับพารามิเตอร์ 6 ตัวและมีลักษณะดังนี้:
__init__(logdir, graph=None, max_queue=10, flush_secs=120, graph_def=None, filename_suffix=None)โดยที่พารามิเตอร์ logdir เป็นสิ่งจำเป็น และส่วนอื่นๆ มีค่าเริ่มต้น พารามิเตอร์กราฟจะถูกส่งต่อจากวัตถุเซสชันที่สร้างขึ้นในโปรแกรมการฝึกอบรม โค้ดตัวอย่างแบบเต็มดูเหมือนว่า:
import tensorflow as tf x = tf.constant(-2.0, name="x", dtype=tf.float32) a = tf.constant(5.0, name="a", dtype=tf.float32) b = tf.constant(13.0, name="b", dtype=tf.float32) y = tf.Variable(tf.add(tf.multiply(a, x), b)) init = tf.global_variables_initializer() with tf.Session() as session: merged = tf.summary.merge_all() // new writer = tf.summary.FileWriter("logs", session.graph) // new session.run(init) print session.run(y) เราเพิ่มเพียงสองบรรทัดใหม่ เรารวมข้อมูลสรุปทั้งหมดที่รวบรวมไว้ในกราฟเริ่มต้น และ FileWriter ใช้เพื่อถ่ายโอนเหตุการณ์ไปยังไฟล์ตามที่เราอธิบายไว้ข้างต้นตามลำดับ
หลังจากรันโปรแกรม เราก็มีไฟล์อยู่ในไดเร็กทอรีล็อก และขั้นตอนสุดท้ายคือการรัน tensorboard :
tensorboard --logdir logs/ ตอนนี้ TensorBoard เริ่มทำงานและทำงานบนพอร์ตเริ่มต้น 6006 หลังจากเปิด http://localhost:6006 และคลิกที่รายการเมนู Graphs (อยู่ที่ด้านบนของหน้า) คุณจะสามารถดูกราฟได้เช่นเดียวกับกราฟ ในภาพด้านล่าง:
TensorBoard ทำเครื่องหมายค่าคงที่และสัญลักษณ์เฉพาะของโหนดสรุป ซึ่งอธิบายไว้ด้านล่าง
คณิตศาสตร์กับ TensorFlow
เทนเซอร์เป็นโครงสร้างข้อมูลพื้นฐานใน TensorFlow และเป็นตัวแทนของขอบที่เชื่อมต่อในกราฟกระแสข้อมูล
เทนเซอร์เพียงระบุอาร์เรย์หรือรายการหลายมิติ โครงสร้างเทนเซอร์สามารถระบุได้ด้วยพารามิเตอร์สามตัว: อันดับ รูปร่าง และประเภท
- อันดับ: ระบุจำนวนมิติของเทนเซอร์ อันดับเรียกว่าลำดับหรือมิติ n ของเทนเซอร์ โดยที่ตัวอย่างอันดับ 1 เทนเซอร์คือเวกเตอร์ หรือเมตริกซ์อันดับ 2 คือเมทริกซ์
- รูปร่าง: รูปร่างของเทนเซอร์คือจำนวนแถวและคอลัมน์ที่มีอยู่
- ชนิด: ชนิดข้อมูลที่กำหนดให้กับองค์ประกอบเทนเซอร์
ในการสร้างเทนเซอร์ใน TensorFlow เราสามารถสร้างอาร์เรย์ n มิติได้ สามารถทำได้ง่ายโดยใช้ไลบรารี NumPy หรือโดยการแปลงอาร์เรย์ n- มิติของ Python เป็นเทนเซอร์ TensorFlow
ในการสร้าง 1-d tensor เราจะใช้อาร์เรย์ NumPy ซึ่งเราจะสร้างโดยส่งรายการ Python ในตัว
import numpy as np tensor_1d = np.array([1.45, -1, 0.2, 102.1])การทำงานกับอาร์เรย์ประเภทนี้คล้ายกับการทำงานกับรายการ Python ในตัว ความแตกต่างหลักคืออาร์เรย์ NumPy ยังมีคุณสมบัติเพิ่มเติมบางอย่าง เช่น มิติ รูปร่าง และประเภท
> > print tensor1d [ 1.45 -1. 0.2 102.1 ] > > print tensor1d[0] 1.45 > > print tensor1d[2] 0.2 > > print tensor1d.ndim 1 > > print tensor1d.shape (4,) > > print tensor1d.dtype float64อาร์เรย์ NumPy สามารถแปลงเป็นเทนเซอร์ TensorFlow ได้อย่างง่ายดายด้วยฟังก์ชันเสริม convert_to_tensor ซึ่งช่วยให้นักพัฒนาแปลงอ็อบเจ็กต์ Python เป็นอ็อบเจ็กต์เทนเซอร์ ฟังก์ชันนี้ยอมรับออบเจ็กต์เทนเซอร์ อาร์เรย์ NumPy รายการ Python และสเกลาร์ของ Python
tensor = tf.convert_to_tensor(tensor_1d, dtype=tf.float64)ตอนนี้ ถ้าเราผูกเทนเซอร์กับเซสชัน TensorFlow เราจะสามารถเห็นผลลัพธ์ของการแปลงของเรา
tensor = tf.convert_to_tensor(tensor_1d, dtype=tf.float64) with tf.Session() as session: print session.run(tensor) print session.run(tensor[0]) print session.run(tensor[1])เอาท์พุท:
[ 1.45 -1. 0.2 102.1 ] 1.45 -1.0เราสามารถสร้างเมตริกซ์ 2 มิติหรือเมทริกซ์ได้ในลักษณะเดียวกัน:
tensor_2d = np.array(np.random.rand(4, 4), dtype='float32') tensor_2d_1 = np.array(np.random.rand(4, 4), dtype='float32') tensor_2d_2 = np.array(np.random.rand(4, 4), dtype='float32') m1 = tf.convert_to_tensor(tensor_2d) m2 = tf.convert_to_tensor(tensor_2d_1) m3 = tf.convert_to_tensor(tensor_2d_2) mat_product = tf.matmul(m1, m2) mat_sum = tf.add(m2, m3) mat_det = tf.matrix_determinant(m3) with tf.Session() as session: print session.run(mat_product) print session.run(mat_sum) print session.run(mat_det)การทำงานของเทนเซอร์
ในตัวอย่างด้านบน เราแนะนำการดำเนินการ TensorFlow สองสามอย่างบนเวกเตอร์และเมทริกซ์ การดำเนินการทำการคำนวณบางอย่างเกี่ยวกับเทนเซอร์ การคำนวณใดบ้างที่แสดงในตารางด้านล่าง
| ตัวดำเนินการเทนเซอร์โฟลว์ | คำอธิบาย |
|---|---|
| tf.add | x+y |
| tf.subtract | xy |
| tf.ทวีคูณ | x*y |
| tf.div | x/y |
| tf.mod | x % y |
| tf.abs | |x| |
| tf.negative | -x |
| tf.sign | เครื่องหมาย(x) |
| tf.square | x*x |
| tf.round | รอบ(x) |
| tf.sqrt | sqrt(x) |
| tf.pow | x^y |
| tf.exp | อี^x |
| tf.log | บันทึก(x) |
| tf.maximum | สูงสุด (x, y) |
| tf.minimum | ขั้นต่ำ(x, y) |
| tf.cos | คอส(x) |
| tf.sin | บาป(x) |
การดำเนินการ TensorFlow ที่แสดงในตารางด้านบนจะทำงานกับออบเจ็กต์เทนเซอร์ และดำเนินการตามองค์ประกอบ ดังนั้น หากคุณต้องการคำนวณโคไซน์สำหรับเวกเตอร์ x การดำเนินการ TensorFlow จะทำการคำนวณสำหรับแต่ละองค์ประกอบในเทนเซอร์ที่ผ่าน

tensor_1d = np.array([0, 0, 0]) tensor = tf.convert_to_tensor(tensor_1d, dtype=tf.float64) with tf.Session() as session: print session.run(tf.cos(tensor))เอาท์พุท:
[ 1. 1. 1.]การดำเนินงานเมทริกซ์
การดำเนินการเมทริกซ์มีความสำคัญมากสำหรับโมเดลแมชชีนเลิร์นนิง เช่น การถดถอยเชิงเส้น เนื่องจากมักใช้ในแบบจำลองเหล่านี้ TensorFlow รองรับการดำเนินการเมทริกซ์ทั่วไปทั้งหมด เช่น การคูณ การทรานสโพส การผกผัน การคำนวณดีเทอร์มีแนนต์ การแก้สมการเชิงเส้น และอื่นๆ อีกมากมาย
ต่อไป เราจะอธิบายการดำเนินการเมทริกซ์บางส่วน สิ่งเหล่านี้มักจะมีความสำคัญเมื่อพูดถึงโมเดลแมชชีนเลิร์นนิง เช่น ในการถดถอยเชิงเส้น ลองเขียนโค้ดที่จะทำการดำเนินการเมทริกซ์พื้นฐาน เช่น การคูณ รับทรานสโพส รับดีเทอร์มีแนนต์ การคูณ โซล และอื่นๆ อีกมากมาย
ด้านล่างนี้เป็นตัวอย่างพื้นฐานของการเรียกการดำเนินการเหล่านี้
import tensorflow as tf import numpy as np def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) m1 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m2 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m3 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m4 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m5 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m_tranpose = tf.transpose(m1) m_mul = tf.matmul(m1, m2) m_det = tf.matrix_determinant(m3) m_inv = tf.matrix_inverse(m4) m_solve = tf.matrix_solve(m5, [[1], [1], [1], [1]]) with tf.Session() as session: print session.run(m_tranpose) print session.run(m_mul) print session.run(m_inv) print session.run(m_det) print session.run(m_solve)การแปลงข้อมูล
การลดน้อยลง
TensorFlow รองรับการลดลงประเภทต่างๆ การลดขนาดเป็นการดำเนินการที่ลบมิติข้อมูลตั้งแต่หนึ่งมิติขึ้นไปออกจากเมตริกซ์โดยดำเนินการบางอย่างในมิติเหล่านั้น รายการการลดลงที่รองรับสำหรับ TensorFlow เวอร์ชันปัจจุบันมีอยู่ที่นี่ เราจะนำเสนอบางส่วนในตัวอย่างด้านล่าง
import tensorflow as tf import numpy as np def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) x = convert( np.array( [ (1, 2, 3), (4, 5, 6), (7, 8, 9) ]), tf.int32) bool_tensor = convert([(True, False, True), (False, False, True), (True, False, False)], tf.bool) red_sum_0 = tf.reduce_sum(x) red_sum = tf.reduce_sum(x, axis=1) red_prod_0 = tf.reduce_prod(x) red_prod = tf.reduce_prod(x, axis=1) red_min_0 = tf.reduce_min(x) red_min = tf.reduce_min(x, axis=1) red_max_0 = tf.reduce_max(x) red_max = tf.reduce_max(x, axis=1) red_mean_0 = tf.reduce_mean(x) red_mean = tf.reduce_mean(x, axis=1) red_bool_all_0 = tf.reduce_all(bool_tensor) red_bool_all = tf.reduce_all(bool_tensor, axis=1) red_bool_any_0 = tf.reduce_any(bool_tensor) red_bool_any = tf.reduce_any(bool_tensor, axis=1) with tf.Session() as session: print "Reduce sum without passed axis parameter: ", session.run(red_sum_0) print "Reduce sum with passed axis=1: ", session.run(red_sum) print "Reduce product without passed axis parameter: ", session.run(red_prod_0) print "Reduce product with passed axis=1: ", session.run(red_prod) print "Reduce min without passed axis parameter: ", session.run(red_min_0) print "Reduce min with passed axis=1: ", session.run(red_min) print "Reduce max without passed axis parameter: ", session.run(red_max_0) print "Reduce max with passed axis=1: ", session.run(red_max) print "Reduce mean without passed axis parameter: ", session.run(red_mean_0) print "Reduce mean with passed axis=1: ", session.run(red_mean) print "Reduce bool all without passed axis parameter: ", session.run(red_bool_all_0) print "Reduce bool all with passed axis=1: ", session.run(red_bool_all) print "Reduce bool any without passed axis parameter: ", session.run(red_bool_any_0) print "Reduce bool any with passed axis=1: ", session.run(red_bool_any)เอาท์พุท:
Reduce sum without passed axis parameter: 45 Reduce sum with passed axis=1: [ 6 15 24] Reduce product without passed axis parameter: 362880 Reduce product with passed axis=1: [ 6 120 504] Reduce min without passed axis parameter: 1 Reduce min with passed axis=1: [1 4 7] Reduce max without passed axis parameter: 9 Reduce max with passed axis=1: [3 6 9] Reduce mean without passed axis parameter: 5 Reduce mean with passed axis=1: [2 5 8] Reduce bool all without passed axis parameter: False Reduce bool all with passed axis=1: [False False False] Reduce bool any without passed axis parameter: True Reduce bool any with passed axis=1: [ True True True]พารามิเตอร์แรกของตัวดำเนินการลดคือเทนเซอร์ที่เราต้องการลด พารามิเตอร์ที่สองคือดัชนีของมิติที่เราต้องการลดขนาด พารามิเตอร์นั้นเป็นทางเลือก และหากไม่ผ่าน การลดจะดำเนินการตามขนาดทั้งหมด
เราสามารถดูการดำเนินการ reduce_sum เราผ่านเทนเซอร์ 2 มิติ และต้องการลดขนาดตามมิติที่ 1
ในกรณีของเรา ผลรวมที่ได้จะเป็น:
[1 + 2 + 3 = 6, 4 + 5 + 6 = 15, 7 + 8 + 9 = 24]หากเราผ่านมิติ 0 ผลลัพธ์จะเป็น:
[1 + 4 + 7 = 12, 2 + 5 + 8 = 15, 3 + 6 + 9 = 18]หากเราไม่ผ่านแกนใดๆ ผลลัพธ์จะเป็นเพียงผลรวมของ:
1 + 4 + 7 = 12, 2 + 5 + 8 = 15, 3 + 6 + 9 = 45ฟังก์ชันการลดทั้งหมดมีส่วนต่อประสานที่คล้ายคลึงกันและแสดงอยู่ในเอกสารประกอบการลด TensorFlow
การแบ่งส่วน
การแบ่งส่วนเป็นกระบวนการที่มิติข้อมูลหนึ่งเป็นกระบวนการของการแมปมิติไปยังดัชนีเซ็กเมนต์ที่มีให้ และองค์ประกอบที่เป็นผลลัพธ์จะถูกกำหนดโดยแถวดัชนี
Segmentation คือการจัดกลุ่มองค์ประกอบภายใต้ดัชนีที่ซ้ำกัน ตัวอย่างเช่น ในกรณีของเรา เราได้แบ่งกลุ่มรหัส [0, 0, 1, 2, 2] ใช้กับเทนเซอร์ tens1 ซึ่งหมายความว่าอาร์เรย์ที่หนึ่งและที่สองจะถูกแปลงตามการแบ่งส่วน operation (ในกรณีของเรา summation) และจะได้อาร์เรย์ใหม่ซึ่งดูเหมือนว่า (2, 8, 1, 0) = (2+0, 5+3, 3-2, -5+5) องค์ประกอบที่สามในเทนเซอร์ tens1 ไม่ถูกแตะต้อง เนื่องจากไม่ได้จัดกลุ่มในดัชนีที่ซ้ำกัน และสองอาร์เรย์สุดท้ายจะถูกรวมในลักษณะเดียวกับกลุ่มแรก นอกจากผลรวมแล้ว TensorFlow ยังสนับสนุนผลิตภัณฑ์ ค่าเฉลี่ย สูงสุด และต่ำสุด
import tensorflow as tf import numpy as np def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) seg_ids = tf.constant([0, 0, 1, 2, 2]) tens1 = convert(np.array([(2, 5, 3, -5), (0, 3, -2, 5), (4, 3, 5, 3), (6, 1, 4, 0), (6, 1, 4, 0)]), tf.int32) tens2 = convert(np.array([1, 2, 3, 4, 5]), tf.int32) seg_sum = tf.segment_sum(tens1, seg_ids) seg_sum_1 = tf.segment_sum(tens2, seg_ids) with tf.Session() as session: print "Segmentation sum tens1: ", session.run(seg_sum) print "Segmentation sum tens2: ", session.run(seg_sum_1) Segmentation sum tens1: [[ 2 8 1 0] [ 4 3 5 3] [12 2 8 0]] Segmentation sum tens2: [3 3 9]ยูทิลิตี้ลำดับ
ยูทิลิตีลำดับรวมถึงวิธีการต่างๆ เช่น:
- ฟังก์ชัน argmin ซึ่งส่งคืนดัชนีที่มีค่าต่ำสุดตามแกนของเทนเซอร์อินพุต
- ฟังก์ชัน argmax ซึ่งส่งคืนดัชนีที่มีค่าสูงสุดข้ามแกนของเทนเซอร์อินพุต
- setdiff ซึ่งคำนวณความแตกต่างระหว่างสองรายการของตัวเลขหรือสตริง
- โดยที่ฟังก์ชันซึ่งจะส่งคืนองค์ประกอบจากองค์ประกอบที่ส่งผ่านสององค์ประกอบ x หรือ y ซึ่งขึ้นอยู่กับเงื่อนไขที่ส่งผ่านหรือ
- ฟังก์ชันเฉพาะ ซึ่งจะส่งคืนองค์ประกอบเฉพาะในเทนเซอร์ 1-D
เราสาธิตตัวอย่างการดำเนินการบางส่วนด้านล่าง:
import numpy as np import tensorflow as tf def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) x = convert(np.array([ [2, 2, 1, 3], [4, 5, 6, -1], [0, 1, 1, -2], [6, 2, 3, 0] ])) y = convert(np.array([1, 2, 5, 3, 7])) z = convert(np.array([1, 0, 4, 6, 2])) arg_min = tf.argmin(x, 1) arg_max = tf.argmax(x, 1) unique = tf.unique(y) diff = tf.setdiff1d(y, z) with tf.Session() as session: print "Argmin = ", session.run(arg_min) print "Argmax = ", session.run(arg_max) print "Unique_values = ", session.run(unique)[0] print "Unique_idx = ", session.run(unique)[1] print "Setdiff_values = ", session.run(diff)[0] print "Setdiff_idx = ", session.run(diff)[1] print session.run(diff)[1]เอาท์พุท:
Argmin = [2 3 3 3] Argmax = [3 2 1 0] Unique_values = [ 1. 2. 5. 3. 7.] Unique_idx = [0 1 2 3 4] Setdiff_values = [ 5. 3. 7.] Setdiff_idx = [2 3 4]แมชชีนเลิร์นนิงด้วย TensorFlow
ในส่วนนี้ เราจะนำเสนอกรณีการใช้งานแมชชีนเลิร์นนิงกับ TensorFlow ตัวอย่างแรกจะเป็นอัลกอริธึมสำหรับการจำแนกข้อมูลด้วยวิธี kNN และตัวอย่างที่สองจะใช้อัลกอริธึมการถดถอยเชิงเส้น
kNN
อัลกอริทึมแรกคือ k-Nearest Neighbors (kNN) เป็นอัลกอริธึมการเรียนรู้ภายใต้การดูแลที่ใช้การวัดระยะทาง เช่น ระยะทางแบบยุคลิด เพื่อจัดประเภทข้อมูลเทียบกับการฝึก เป็นหนึ่งในอัลกอริธึมที่ง่ายที่สุด แต่ก็ยังมีประสิทธิภาพมากในการจำแนกข้อมูล ข้อดีของอัลกอริทึมนี้:
- ให้ความแม่นยำสูงเมื่อโมเดลการฝึกมีขนาดใหญ่พอ และ
- โดยปกติแล้วจะไม่มีความละเอียดอ่อนต่อค่าผิดปกติ และเราไม่จำเป็นต้องมีข้อสันนิษฐานใดๆ เกี่ยวกับข้อมูล
ข้อเสียของอัลกอริทึมนี้:
- แพงในการคำนวณและ
- ต้องใช้หน่วยความจำจำนวนมากซึ่งจำเป็นต้องเพิ่มข้อมูลที่จัดประเภทใหม่ให้กับอินสแตนซ์การฝึกเริ่มต้นทั้งหมด
ระยะทางที่เราจะใช้ในตัวอย่างโค้ดนี้คือ Euclidean ซึ่งกำหนดระยะห่างระหว่างจุดสองจุดดังนี้:
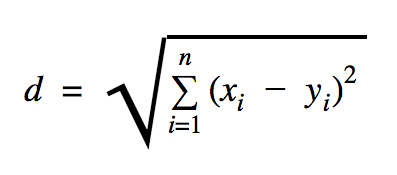
ในสูตรนี้ n คือจำนวนมิติของช่องว่าง x คือเวกเตอร์ของข้อมูลการฝึก และ y เป็นจุดข้อมูลใหม่ที่เราต้องการจัดประเภท
import os import numpy as np import tensorflow as tf ccf_train_data = "train_dataset.csv" ccf_test_data = "test_dataset.csv" dataset_dir = os.path.abspath(os.path.join(os.path.dirname(__file__), '../datasets')) ccf_train_filepath = os.path.join(dataset_dir, ccf_train_data) ccf_test_filepath = os.path.join(dataset_dir, ccf_test_data) def load_data(filepath): from numpy import genfromtxt csv_data = genfromtxt(filepath, delimiter=",", skip_header=1) data = [] labels = [] for d in csv_data: data.append(d[:-1]) labels.append(d[-1]) return np.array(data), np.array(labels) train_dataset, train_labels = load_data(ccf_train_filepath) test_dataset, test_labels = load_data(ccf_test_filepath) train_pl = tf.placeholder("float", [None, 28]) test_pl = tf.placeholder("float", [28]) knn_prediction = tf.reduce_sum(tf.abs(tf.add(train_pl, tf.negative(test_pl))), axis=1) pred = tf.argmin(knn_prediction, 0) with tf.Session() as tf_session: missed = 0 for i in xrange(len(test_dataset)): knn_index = tf_session.run(pred, feed_dict={train_pl: train_dataset, test_pl: test_dataset[i]}) print "Predicted class {} -- True class {}".format(train_labels[knn_index], test_labels[i]) if train_labels[knn_index] != test_labels[i]: missed += 1 tf.summary.FileWriter("../samples/article/logs", tf_session.graph) print "Missed: {} -- Total: {}".format(missed, len(test_dataset))ชุดข้อมูลที่เราใช้ในตัวอย่างข้างต้นเป็นชุดข้อมูลที่สามารถพบได้ในส่วนชุดข้อมูล Kaggle เราใช้รายการที่มีการทำธุรกรรมด้วยบัตรเครดิตของผู้ถือบัตรชาวยุโรป เรากำลังใช้ข้อมูลโดยไม่มีการทำความสะอาดหรือการกรองใดๆ และตามคำอธิบายใน Kaggle สำหรับชุดข้อมูลนี้ ข้อมูลนั้นไม่สมดุลอย่างมาก ชุดข้อมูลประกอบด้วยตัวแปร 31 ตัว: เวลา, V1, …, V28, จำนวน และคลาส ในโค้ดตัวอย่างนี้ เราใช้ V1, …, V28 และ Class เท่านั้น ธุรกรรมประเภทป้ายกำกับที่ฉ้อโกงกับ 1 และธุรกรรมที่ไม่ใช่ 0
ตัวอย่างโค้ดประกอบด้วยสิ่งต่างๆ ที่เราอธิบายไว้ในส่วนก่อนหน้าเป็นส่วนใหญ่ ยกเว้นในกรณีที่เราแนะนำฟังก์ชันสำหรับการโหลดชุดข้อมูล ฟังก์ชัน load_data(filepath) จะใช้ไฟล์ CSV เป็นอาร์กิวเมนต์ และจะส่งคืน tuple พร้อมข้อมูลและป้ายกำกับที่กำหนดไว้ใน CSV
ด้านล่างฟังก์ชันนั้น เราได้กำหนดตัวยึดตำแหน่งสำหรับการทดสอบและข้อมูลที่ได้รับการฝึกอบรมแล้ว ข้อมูลที่ได้รับการฝึกอบรมจะใช้ในแบบจำลองการคาดการณ์เพื่อแก้ไขป้ายกำกับสำหรับข้อมูลที่ป้อนเข้าซึ่งจำเป็นต้องจัดประเภท ในกรณีของเรา kNN ใช้ระยะทางแบบยุคลิเดียนเพื่อให้ได้ป้ายกำกับที่ใกล้ที่สุด
อัตราความผิดพลาดสามารถคำนวณได้โดยการหารอย่างง่ายด้วยตัวเลขเมื่อตัวแยกประเภทพลาดโดยจำนวนตัวอย่างทั้งหมด ซึ่งในกรณีของเราสำหรับชุดข้อมูลนี้คือ 0.2 (กล่าวคือ ตัวแยกประเภทให้ป้ายกำกับข้อมูลที่ไม่ถูกต้องสำหรับ 20% ของข้อมูลทดสอบ)
การถดถอยเชิงเส้น
อัลกอริธึมการถดถอยเชิงเส้นจะค้นหาความสัมพันธ์เชิงเส้นระหว่างตัวแปรสองตัว หากเรากำหนดตัวแปรตามเป็น y และตัวแปรอิสระเป็น x แสดงว่าเรากำลังพยายามประมาณค่าพารามิเตอร์ของฟังก์ชัน y = Wx + b
การถดถอยเชิงเส้นเป็นอัลกอริทึมที่ใช้กันอย่างแพร่หลายในด้านวิทยาศาสตร์ประยุกต์ อัลกอริธึมนี้อนุญาตให้เพิ่มแนวคิดที่สำคัญสองประการของการเรียนรู้ของเครื่อง: ฟังก์ชันต้นทุนและวิธีลาดลงสำหรับการค้นหาฟังก์ชันขั้นต่ำ
อัลกอริธึมการเรียนรู้ของเครื่องที่ใช้วิธีนี้จะต้องทำนายค่าของ y เป็นฟังก์ชันของ x โดยที่อัลกอริธึมการถดถอยเชิงเส้นจะกำหนดค่า W และ b ซึ่งไม่ทราบจริง ๆ แล้วถูกกำหนดโดยกระบวนการฝึกอบรม มีการเลือกฟังก์ชันต้นทุน และมักจะใช้ค่าคลาดเคลื่อนกำลังสองเฉลี่ย โดยที่การไล่ระดับลงเป็นอัลกอริธึมการปรับให้เหมาะสมที่ใช้เพื่อค้นหาฟังก์ชันต้นทุนขั้นต่ำในพื้นที่
วิธีการ gradient descent เป็นฟังก์ชันขั้นต่ำในเครื่องเท่านั้น แต่สามารถใช้ในการค้นหาค่าต่ำสุดทั่วโลกได้โดยการสุ่มเลือกจุดเริ่มต้นใหม่เมื่อพบค่าต่ำสุดในเครื่องแล้วและทำขั้นตอนนี้ซ้ำหลายครั้ง หากจำนวนขั้นต่ำของฟังก์ชันมีจำกัดและมีจำนวนครั้งในการดำเนินการสูงมาก ก็มีโอกาสสูงที่จุดใดจุดหนึ่งจะพบจุดต่ำสุดทั่วโลก เราจะพูดถึงรายละเอียดเพิ่มเติมเกี่ยวกับเทคนิคนี้สำหรับบทความที่เรากล่าวถึงในส่วนแนะนำ
import tensorflow as tf import numpy as np test_data_size = 2000 iterations = 10000 learn_rate = 0.005 def generate_test_values(): train_x = [] train_y = [] for _ in xrange(test_data_size): x1 = np.random.rand() x2 = np.random.rand() x3 = np.random.rand() y_f = 2 * x1 + 3 * x2 + 7 * x3 + 4 train_x.append([x1, x2, x3]) train_y.append(y_f) return np.array(train_x), np.transpose([train_y]) x = tf.placeholder(tf.float32, [None, 3], name="x") W = tf.Variable(tf.zeros([3, 1]), name="W") b = tf.Variable(tf.zeros([1]), name="b") y = tf.placeholder(tf.float32, [None, 1]) model = tf.add(tf.matmul(x, W), b) cost = tf.reduce_mean(tf.square(y - model)) train = tf.train.GradientDescentOptimizer(learn_rate).minimize(cost) train_dataset, train_values = generate_test_values() init = tf.global_variables_initializer() with tf.Session() as session: session.run(init) for _ in xrange(iterations): session.run(train, feed_dict={ x: train_dataset, y: train_values }) print "cost = {}".format(session.run(cost, feed_dict={ x: train_dataset, y: train_values })) print "W = {}".format(session.run(W)) print "b = {}".format(session.run(b))เอาท์พุท:
cost = 3.1083032809e-05 W = [[ 1.99049103] [ 2.9887135 ] [ 6.98754263]] b = [ 4.01742554] ในตัวอย่างข้างต้น เรามีตัวแปรใหม่ 2 ตัว ซึ่งเราเรียกว่า cost and train ด้วยตัวแปรทั้งสองนี้ เราได้กำหนดตัวเพิ่มประสิทธิภาพซึ่งเราต้องการใช้ในแบบจำลองการฝึกของเราและฟังก์ชันที่เราต้องการย่อให้เล็กสุด
ในตอนท้าย พารามิเตอร์เอาต์พุตของ W และ b ควรเหมือนกันกับที่กำหนดไว้ในฟังก์ชัน generate_test_values ในบรรทัดที่ 17 เรากำหนดฟังก์ชันที่เราใช้ในการสร้างจุดข้อมูลเชิงเส้นเพื่อฝึกโดยที่ w1=2 , w2=3 , w3=7 และ b=4 การถดถอยเชิงเส้นจากตัวอย่างข้างต้นเป็นแบบพหุตัวแปรซึ่งมีการใช้ตัวแปรอิสระมากกว่าหนึ่งตัว
บทสรุป
ดังที่คุณเห็นจากบทช่วยสอน TensorFlow นี้ TensorFlow เป็นเฟรมเวิร์กที่ทรงพลังที่ทำให้การทำงานกับนิพจน์ทางคณิตศาสตร์และอาร์เรย์หลายมิติเป็นเรื่องง่าย ซึ่งเป็นสิ่งจำเป็นพื้นฐานในการเรียนรู้ของเครื่อง นอกจากนี้ยังสรุปความซับซ้อนของการดำเนินการกราฟข้อมูลและการปรับขนาด
เมื่อเวลาผ่านไป TensorFlow ได้รับความนิยมมากขึ้นเรื่อยๆ และตอนนี้นักพัฒนากำลังใช้แก้ปัญหาโดยใช้วิธีการเรียนรู้เชิงลึกในการจดจำรูปภาพ การตรวจจับวิดีโอ การประมวลผลข้อความ เช่น การวิเคราะห์ความรู้สึก เป็นต้น เช่นเดียวกับห้องสมุดอื่นๆ คุณอาจต้องใช้เวลาสักพักจึงจะชิน กับแนวคิดที่ TensorFlow สร้างขึ้น และเมื่อคุณทำสำเร็จแล้ว ด้วยความช่วยเหลือของเอกสารประกอบและการสนับสนุนจากชุมชน การแสดงปัญหาเป็นกราฟข้อมูลและการแก้ปัญหาด้วย TensorFlow จะทำให้การเรียนรู้ของเครื่องในวงกว้างมีกระบวนการที่น่าเบื่อน้อยลง
