Premiers pas avec TensorFlow : un didacticiel d'apprentissage automatique
Publié: 2022-03-11TensorFlow est une bibliothèque de logiciels open source créée par Google qui est utilisée pour mettre en œuvre des systèmes d'apprentissage automatique et d'apprentissage en profondeur. Ces deux noms contiennent une série d'algorithmes puissants qui partagent un défi commun : permettre à un ordinateur d'apprendre à repérer automatiquement des modèles complexes et/ou à prendre les meilleures décisions possibles.
Si vous souhaitez en savoir plus sur ces systèmes, vous pouvez en savoir plus sur les articles du blog Toptal sur l'apprentissage automatique et l'apprentissage en profondeur.
TensorFlow, en son cœur, est une bibliothèque pour la programmation de flux de données. Il s'appuie sur diverses techniques d'optimisation pour rendre le calcul des expressions mathématiques plus facile et plus performant.
Certaines des fonctionnalités clés de TensorFlow sont :
- Fonctionne efficacement avec des expressions mathématiques impliquant des tableaux multidimensionnels
- Bon support des réseaux de neurones profonds et des concepts d'apprentissage automatique
- Calcul GPU/CPU où le même code peut être exécuté sur les deux architectures
- Haute évolutivité du calcul sur les machines et sur d'énormes ensembles de données
Ensemble, ces fonctionnalités font de TensorFlow le cadre idéal pour l'intelligence artificielle à l'échelle de la production.
Dans ce didacticiel TensorFlow, vous apprendrez comment vous pouvez utiliser des méthodes d'apprentissage automatique simples mais puissantes dans TensorFlow et comment vous pouvez utiliser certaines de ses bibliothèques auxiliaires pour déboguer, visualiser et ajuster les modèles créés avec.
Installer TensorFlow
Nous utiliserons l'API Python TensorFlow, qui fonctionne avec Python 2.7 et Python 3.3+. La version GPU (Linux uniquement) nécessite le Cuda Toolkit 7.0+ et cuDNN v2+.
Nous utiliserons le système de gestion des dépendances du package Conda pour installer TensorFlow. Conda nous permet de séparer plusieurs environnements sur une machine. Vous pouvez apprendre à installer Conda à partir d'ici.
Après avoir installé Conda, nous pouvons créer l'environnement que nous utiliserons pour l'installation et l'utilisation de TensorFlow. La commande suivante créera notre environnement avec quelques bibliothèques supplémentaires comme NumPy, ce qui est très utile une fois que nous commençons à utiliser TensorFlow.
La version de Python installée dans cet environnement est la 2.7, et nous utiliserons cette version dans cet article.
conda create --name TensorflowEnv biopython Pour faciliter les choses, nous installons biopython ici au lieu de simplement NumPy. Cela inclut NumPy et quelques autres packages dont nous aurons besoin. Vous pouvez toujours installer les packages selon vos besoins à l'aide des conda install ou pip install .
La commande suivante activera l'environnement Conda créé. Nous pourrons utiliser les packages installés à l'intérieur, sans mélanger avec les packages installés globalement ou dans d'autres environnements.
source activate TensorFlowEnvL'outil d'installation pip fait partie intégrante d'un environnement Conda. Nous allons l'utiliser pour installer la bibliothèque TensorFlow. Avant de faire cela, une bonne première étape consiste à mettre à jour pip vers la dernière version, en utilisant la commande suivante :
pip install --upgrade pipNous sommes maintenant prêts à installer TensorFlow, en exécutant :
pip install tensorflowLe téléchargement et la création de TensorFlow peuvent prendre plusieurs minutes. Au moment de la rédaction, cela installe TensorFlow 1.1.0.
Graphiques de flux de données
Dans TensorFlow, le calcul est décrit à l'aide de graphes de flux de données. Chaque nœud du graphique représente une instance d'une opération mathématique (comme l'addition, la division ou la multiplication) et chaque arête est un ensemble de données multidimensionnelles (tenseur) sur lequel les opérations sont effectuées.
Comme TensorFlow fonctionne avec des graphes de calcul, ils sont gérés là où chaque nœud représente l'instanciation d'une opération où chaque opération a zéro ou plusieurs entrées et zéro ou plusieurs sorties.
Les bords dans TensorFlow peuvent être regroupés en deux catégories : les bords normaux transfèrent la structure de données (tenseurs) où il est possible que la sortie d'une opération devienne l'entrée d'une autre opération et les bords spéciaux, qui sont utilisés pour contrôler la dépendance entre deux nœuds pour définir le ordre d'opération où un nœud attend qu'un autre se termine.
Expressions simples
Avant de passer à la discussion des éléments de TensorFlow, nous allons d'abord faire une session de travail avec TensorFlow, pour avoir une idée de ce à quoi ressemble un programme TensorFlow.
Commençons par des expressions simples et supposons que, pour une raison quelconque, nous souhaitons évaluer la fonction y = 5*x + 13 à la manière de TensorFlow.
Dans un code Python simple, cela ressemblerait à :
x = -2.0 y = 5*x + 13 print yce qui nous donne dans ce cas un résultat de 3,0.
Nous allons maintenant convertir l'expression ci-dessus en termes TensorFlow.
Constantes
Dans TensorFlow, les constantes sont créées à l'aide de la fonction constant, qui a la signature constant(value, dtype=None, shape=None, name='Const', verify_shape=False) , où value est une valeur constante réelle qui sera utilisée dans calcul ultérieur, dtype est le paramètre de type de données (par exemple, float32/64, int8/16, etc.), shape est des dimensions facultatives, name est un nom facultatif pour le tenseur et le dernier paramètre est un booléen qui indique la vérification de la forme de valeurs.
Si vous avez besoin de constantes avec des valeurs spécifiques dans votre modèle d'entraînement, l'objet constant peut être utilisé comme dans l'exemple suivant :
z = tf.constant(5.2, name="x", dtype=tf.float32)variables
Les variables dans TensorFlow sont des tampons en mémoire contenant des tenseurs qui doivent être explicitement initialisés et utilisés dans le graphique pour maintenir l'état d'une session à l'autre. En appelant simplement le constructeur, la variable est ajoutée dans le graphe de calcul.
Les variables sont particulièrement utiles une fois que vous commencez avec des modèles d'entraînement, et elles sont utilisées pour conserver et mettre à jour les paramètres. Une valeur initiale passée en argument d'un constructeur représente un tenseur ou un objet qui peut être converti ou renvoyé en tant que tenseur. Cela signifie que si nous voulons remplir une variable avec des valeurs prédéfinies ou aléatoires à utiliser ensuite dans le processus d'apprentissage et mises à jour au fil des itérations, nous pouvons la définir de la manière suivante :
k = tf.Variable(tf.zeros([1]), name="k")Une autre façon d'utiliser des variables dans TensorFlow consiste à effectuer des calculs où cette variable ne peut pas être entraînée et peut être définie de la manière suivante :
k = tf.Variable(tf.add(a, b), trainable=False)Séances
Afin d'évaluer réellement les nœuds, nous devons exécuter un graphe de calcul dans une session.
Une session encapsule le contrôle et l'état de l'environnement d'exécution TensorFlow. Une session sans paramètres utilisera le graphe par défaut créé dans la session en cours, sinon la classe de session accepte un paramètre de graphe, qui est utilisé dans cette session pour être exécuté.
Vous trouverez ci-dessous un bref extrait de code qui montre comment les termes définis ci-dessus peuvent être utilisés dans TensorFlow pour calculer une fonction linéaire simple.
import tensorflow as tf x = tf.constant(-2.0, name="x", dtype=tf.float32) a = tf.constant(5.0, name="a", dtype=tf.float32) b = tf.constant(13.0, name="b", dtype=tf.float32) y = tf.Variable(tf.add(tf.multiply(a, x), b)) init = tf.global_variables_initializer() with tf.Session() as session: session.run(init) print session.run(y)Utiliser TensorFlow : définir des graphes de calcul
La bonne chose à propos de travailler avec des graphiques de flux de données est que le modèle d'exécution est séparé de son exécution (sur CPU, GPU ou une combinaison) où, une fois implémenté, le logiciel dans TensorFlow peut être utilisé sur le CPU ou le GPU où toute la complexité liée au code l'exécution est masquée.
Le graphe de calcul peut être créé lors du processus d'utilisation de la bibliothèque TensorFlow sans avoir à instancier explicitement des objets Graph.
Un objet Graph dans TensorFlow peut être créé à la suite d'une simple ligne de code comme c = tf.add(a, b) . Cela créera un nœud d'opération qui prend deux tenseurs a et b qui produisent leur somme c en sortie.
Le graphe de calcul est un processus intégré qui utilise la bibliothèque sans avoir besoin d'appeler directement l'objet graphe. Un objet graphique dans TensorFlow, qui contient un ensemble d'opérations et de tenseurs en tant qu'unités de données, est utilisé entre les opérations qui permettent le même processus et contient plus d'un graphique où chaque graphique sera affecté à une session différente. Par exemple, la simple ligne de code c = tf.add(a, b) créera un nœud d'opération qui prend deux tenseurs a et b en entrée et produit leur somme c en sortie.
TensorFlow fournit également un mécanisme d'alimentation pour appliquer un tenseur à n'importe quelle opération du graphique, où l'alimentation remplace la sortie d'une opération par la valeur du tenseur. Les données du flux sont transmises en tant qu'argument dans l'appel de la fonction run() .
Un espace réservé est la façon dont TensorFlow permet aux développeurs d'injecter des données dans le graphe de calcul via des espaces réservés qui sont liés à l'intérieur de certaines expressions. La signature de l'espace réservé est :
placeholder(dtype, shape=None, name=None)où dtype est le type d'éléments dans les tenseurs et peut fournir à la fois la forme des tenseurs à alimenter et le nom de l'opération.
Si la forme n'est pas passée, ce tenseur peut être alimenté avec n'importe quelle forme. Une remarque importante est que le tenseur d'espace réservé doit être alimenté avec des données, sinon, lors de l'exécution de la session et si cette partie est manquante, l'espace réservé génère une erreur avec la structure suivante :
InvalidArgumentError (see above for traceback): You must feed a value for placeholder tensor 'y' with dtype floatL'avantage des espaces réservés est qu'ils permettent aux développeurs de créer des opérations, et le graphe de calcul en général, sans avoir besoin de fournir les données à l'avance pour cela, et les données peuvent être ajoutées en cours d'exécution à partir de sources externes.
Prenons un problème simple de multiplication de deux entiers x et y à la manière de TensorFlow, où un espace réservé sera utilisé avec un mécanisme d'alimentation via la méthode run de session.
import tensorflow as tf x = tf.placeholder(tf.float32, name="x") y = tf.placeholder(tf.float32, name="y") z = tf.multiply(x, y, name="z") with tf.Session() as session: print session.run(z, feed_dict={x: 2.1, y: 3.0})Visualiser le graphe de calcul avec TensorBoard
TensorBoard est un outil de visualisation pour analyser les graphiques de flux de données. Cela peut être utile pour mieux comprendre les modèles d'apprentissage automatique.
Avec TensorBoard, vous pouvez avoir un aperçu de différents types de statistiques sur les paramètres et des détails sur les parties du graphe de calcul en général. Il n'est pas rare qu'un réseau neuronal profond ait un grand nombre de nœuds. TensorBoard permet aux développeurs d'avoir un aperçu de chaque nœud et de la façon dont le calcul est exécuté sur l'environnement d'exécution TensorFlow.
Revenons maintenant à notre exemple du début de ce tutoriel TensorFlow où nous avons défini une fonction linéaire au format y = a*x + b .
Afin de consigner les événements de la session qui pourront ensuite être utilisés dans TensorBoard, TensorFlow fournit la classe FileWriter . Il peut être utilisé pour créer un fichier d'événements pour stocker des résumés où le constructeur accepte six paramètres et ressemble à :
__init__(logdir, graph=None, max_queue=10, flush_secs=120, graph_def=None, filename_suffix=None)où le paramètre logdir est requis, et d'autres ont des valeurs par défaut. Le paramètre graphique sera transmis à partir de l'objet de session créé dans le programme de formation. L'exemple de code complet ressemble à :
import tensorflow as tf x = tf.constant(-2.0, name="x", dtype=tf.float32) a = tf.constant(5.0, name="a", dtype=tf.float32) b = tf.constant(13.0, name="b", dtype=tf.float32) y = tf.Variable(tf.add(tf.multiply(a, x), b)) init = tf.global_variables_initializer() with tf.Session() as session: merged = tf.summary.merge_all() // new writer = tf.summary.FileWriter("logs", session.graph) // new session.run(init) print session.run(y) Nous avons ajouté seulement deux nouvelles lignes. Nous fusionnons tous les résumés collectés dans le graphique par défaut, et FileWriter est utilisé pour vider les événements dans le fichier comme nous l'avons décrit ci-dessus, respectivement.
Après avoir exécuté le programme, nous avons le fichier dans le répertoire logs, et la dernière étape consiste à exécuter tensorboard :
tensorboard --logdir logs/ Maintenant, TensorBoard est démarré et fonctionne sur le port par défaut 6006. Après avoir ouvert http://localhost:6006 et cliqué sur l'élément de menu Graphiques (situé en haut de la page), vous pourrez voir le graphique, comme celui dans l'image ci-dessous :
TensorBoard marque les constantes et les symboles spécifiques aux nœuds récapitulatifs, qui sont décrits ci-dessous.
Mathématiques avec TensorFlow
Les tenseurs sont les structures de données de base dans TensorFlow, et ils représentent les arêtes de connexion dans un graphe de flux de données.
Un tenseur identifie simplement un tableau ou une liste multidimensionnelle. La structure tensorielle peut être identifiée par trois paramètres : rang, forme et type.
- Rang : Identifie le nombre de dimensions du tenseur. Un rang est connu comme l'ordre ou les n dimensions d'un tenseur, où par exemple le tenseur de rang 1 est un vecteur ou le tenseur de rang 2 est une matrice.
- Forme : La forme d'un tenseur est le nombre de lignes et de colonnes dont il dispose.
- Type : type de données affecté aux éléments Tensor.
Pour créer un tenseur dans TensorFlow, nous pouvons créer un tableau à n dimensions. Cela peut être fait facilement en utilisant la bibliothèque NumPy ou en convertissant un tableau Python à n dimensions en un tenseur TensorFlow.
Pour construire un tenseur 1-d, nous utiliserons un tableau NumPy, que nous construirons en passant une liste Python intégrée.
import numpy as np tensor_1d = np.array([1.45, -1, 0.2, 102.1])Travailler avec ce type de tableau est similaire à travailler avec une liste Python intégrée. La principale différence est que le tableau NumPy contient également des propriétés supplémentaires, telles que la dimension, la forme et le type.
> > print tensor1d [ 1.45 -1. 0.2 102.1 ] > > print tensor1d[0] 1.45 > > print tensor1d[2] 0.2 > > print tensor1d.ndim 1 > > print tensor1d.shape (4,) > > print tensor1d.dtype float64Un tableau NumPy peut être facilement converti en un tenseur TensorFlow avec la fonction auxiliaire convert_to_tensor, qui aide les développeurs à convertir des objets Python en objets tenseurs. Cette fonction accepte les objets tensoriels, les tableaux NumPy, les listes Python et les scalaires Python.
tensor = tf.convert_to_tensor(tensor_1d, dtype=tf.float64)Maintenant, si nous lions notre tenseur à la session TensorFlow, nous pourrons voir les résultats de notre conversion.
tensor = tf.convert_to_tensor(tensor_1d, dtype=tf.float64) with tf.Session() as session: print session.run(tensor) print session.run(tensor[0]) print session.run(tensor[1])Sortir:
[ 1.45 -1. 0.2 102.1 ] 1.45 -1.0Nous pouvons créer un tenseur 2D, ou une matrice, de la même manière :
tensor_2d = np.array(np.random.rand(4, 4), dtype='float32') tensor_2d_1 = np.array(np.random.rand(4, 4), dtype='float32') tensor_2d_2 = np.array(np.random.rand(4, 4), dtype='float32') m1 = tf.convert_to_tensor(tensor_2d) m2 = tf.convert_to_tensor(tensor_2d_1) m3 = tf.convert_to_tensor(tensor_2d_2) mat_product = tf.matmul(m1, m2) mat_sum = tf.add(m2, m3) mat_det = tf.matrix_determinant(m3) with tf.Session() as session: print session.run(mat_product) print session.run(mat_sum) print session.run(mat_det)Opérations tensorielles
Dans l'exemple ci-dessus, nous introduisons quelques opérations TensorFlow sur les vecteurs et les matrices. Les opérations effectuent certains calculs sur les tenseurs. Ces calculs sont indiqués dans le tableau ci-dessous.
| Opérateur TensorFlow | La description |
|---|---|
| tf.add | x+y |
| tf. soustraire | xy |
| tf.multiplier | x*y |
| tf.div | x/y |
| tf.mod | x % y |
| tf.abs | |x| |
| tf.négatif | -X |
| tf.sign | signe(x) |
| tf.carré | x*x |
| tf.rond | rond(x) |
| tf.sqrt | m²(x) |
| tf.pow | x^y |
| tf.exp | e^x |
| tf.log | log(x) |
| tf.maximum | max(x, y) |
| tf.minimum | min(x, y) |
| tf.cos | cos(x) |
| tf.sin | péché(x) |
Les opérations TensorFlow répertoriées dans le tableau ci-dessus fonctionnent avec des objets Tensor et sont effectuées élément par élément. Ainsi, si vous souhaitez calculer le cosinus d'un vecteur x, l'opération TensorFlow effectuera des calculs pour chaque élément du tenseur passé.

tensor_1d = np.array([0, 0, 0]) tensor = tf.convert_to_tensor(tensor_1d, dtype=tf.float64) with tf.Session() as session: print session.run(tf.cos(tensor))Sortir:
[ 1. 1. 1.]Opérations matricielles
Les opérations matricielles sont très importantes pour les modèles d'apprentissage automatique, comme la régression linéaire, car elles y sont souvent utilisées. TensorFlow prend en charge toutes les opérations matricielles les plus courantes, telles que la multiplication, la transposition, l'inversion, le calcul du déterminant, la résolution d'équations linéaires, etc.
Ensuite, nous expliquerons certaines des opérations matricielles. Ils ont tendance à être importants lorsqu'il s'agit de modèles d'apprentissage automatique, comme dans la régression linéaire. Écrivons du code qui effectuera des opérations matricielles de base comme la multiplication, l'obtention de la transposition, l'obtention du déterminant, la multiplication, le sol et bien d'autres.
Vous trouverez ci-dessous des exemples de base d'appel de ces opérations.
import tensorflow as tf import numpy as np def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) m1 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m2 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m3 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m4 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m5 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m_tranpose = tf.transpose(m1) m_mul = tf.matmul(m1, m2) m_det = tf.matrix_determinant(m3) m_inv = tf.matrix_inverse(m4) m_solve = tf.matrix_solve(m5, [[1], [1], [1], [1]]) with tf.Session() as session: print session.run(m_tranpose) print session.run(m_mul) print session.run(m_inv) print session.run(m_det) print session.run(m_solve)Transformer les données
Réduction
TensorFlow prend en charge différents types de réduction. La réduction est une opération qui supprime une ou plusieurs dimensions d'un tenseur en effectuant certaines opérations sur ces dimensions. Une liste des réductions prises en charge pour la version actuelle de TensorFlow est disponible ici. Nous en présentons quelques-unes dans l'exemple ci-dessous.
import tensorflow as tf import numpy as np def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) x = convert( np.array( [ (1, 2, 3), (4, 5, 6), (7, 8, 9) ]), tf.int32) bool_tensor = convert([(True, False, True), (False, False, True), (True, False, False)], tf.bool) red_sum_0 = tf.reduce_sum(x) red_sum = tf.reduce_sum(x, axis=1) red_prod_0 = tf.reduce_prod(x) red_prod = tf.reduce_prod(x, axis=1) red_min_0 = tf.reduce_min(x) red_min = tf.reduce_min(x, axis=1) red_max_0 = tf.reduce_max(x) red_max = tf.reduce_max(x, axis=1) red_mean_0 = tf.reduce_mean(x) red_mean = tf.reduce_mean(x, axis=1) red_bool_all_0 = tf.reduce_all(bool_tensor) red_bool_all = tf.reduce_all(bool_tensor, axis=1) red_bool_any_0 = tf.reduce_any(bool_tensor) red_bool_any = tf.reduce_any(bool_tensor, axis=1) with tf.Session() as session: print "Reduce sum without passed axis parameter: ", session.run(red_sum_0) print "Reduce sum with passed axis=1: ", session.run(red_sum) print "Reduce product without passed axis parameter: ", session.run(red_prod_0) print "Reduce product with passed axis=1: ", session.run(red_prod) print "Reduce min without passed axis parameter: ", session.run(red_min_0) print "Reduce min with passed axis=1: ", session.run(red_min) print "Reduce max without passed axis parameter: ", session.run(red_max_0) print "Reduce max with passed axis=1: ", session.run(red_max) print "Reduce mean without passed axis parameter: ", session.run(red_mean_0) print "Reduce mean with passed axis=1: ", session.run(red_mean) print "Reduce bool all without passed axis parameter: ", session.run(red_bool_all_0) print "Reduce bool all with passed axis=1: ", session.run(red_bool_all) print "Reduce bool any without passed axis parameter: ", session.run(red_bool_any_0) print "Reduce bool any with passed axis=1: ", session.run(red_bool_any)Sortir:
Reduce sum without passed axis parameter: 45 Reduce sum with passed axis=1: [ 6 15 24] Reduce product without passed axis parameter: 362880 Reduce product with passed axis=1: [ 6 120 504] Reduce min without passed axis parameter: 1 Reduce min with passed axis=1: [1 4 7] Reduce max without passed axis parameter: 9 Reduce max with passed axis=1: [3 6 9] Reduce mean without passed axis parameter: 5 Reduce mean with passed axis=1: [2 5 8] Reduce bool all without passed axis parameter: False Reduce bool all with passed axis=1: [False False False] Reduce bool any without passed axis parameter: True Reduce bool any with passed axis=1: [ True True True]Le premier paramètre des opérateurs de réduction est le tenseur que l'on veut réduire. Le deuxième paramètre est les indices de dimensions le long desquels on veut effectuer la réduction. Ce paramètre est facultatif et s'il n'est pas passé, la réduction sera effectuée sur toutes les dimensions.
Nous pouvons jeter un œil à l'opération reduce_sum. Nous passons un tenseur 2D et voulons le réduire le long de la dimension 1.
Dans notre cas, la somme résultante serait :
[1 + 2 + 3 = 6, 4 + 5 + 6 = 15, 7 + 8 + 9 = 24]Si nous passions la dimension 0, le résultat serait :
[1 + 4 + 7 = 12, 2 + 5 + 8 = 15, 3 + 6 + 9 = 18]Si nous ne transmettons aucun axe, le résultat est simplement la somme globale de :
1 + 4 + 7 = 12, 2 + 5 + 8 = 15, 3 + 6 + 9 = 45Toutes les fonctions de réduction ont une interface similaire et sont répertoriées dans la documentation de réduction TensorFlow.
Segmentation
La segmentation est un processus dans lequel l'une des dimensions est le processus de mappage des dimensions sur les index de segment fournis, et les éléments résultants sont déterminés par une ligne d'index.
La segmentation regroupe en fait les éléments sous des index répétés, donc par exemple, dans notre cas, nous avons des identifiants segmentés [0, 0, 1, 2, 2] appliqués sur le tenseur tens1 , ce qui signifie que les premier et deuxième tableaux seront transformés après la segmentation opération (dans notre cas la sommation) et obtiendra un nouveau tableau, qui ressemble à (2, 8, 1, 0) = (2+0, 5+3, 3-2, -5+5) . Le troisième élément du tenseur tens1 n'est pas touché car il n'est groupé dans aucun index répété, et les deux derniers tableaux sont additionnés de la même manière que c'était le cas pour le premier groupe. Outre la sommation, TensorFlow prend en charge le produit, la moyenne, le max et le min.
import tensorflow as tf import numpy as np def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) seg_ids = tf.constant([0, 0, 1, 2, 2]) tens1 = convert(np.array([(2, 5, 3, -5), (0, 3, -2, 5), (4, 3, 5, 3), (6, 1, 4, 0), (6, 1, 4, 0)]), tf.int32) tens2 = convert(np.array([1, 2, 3, 4, 5]), tf.int32) seg_sum = tf.segment_sum(tens1, seg_ids) seg_sum_1 = tf.segment_sum(tens2, seg_ids) with tf.Session() as session: print "Segmentation sum tens1: ", session.run(seg_sum) print "Segmentation sum tens2: ", session.run(seg_sum_1) Segmentation sum tens1: [[ 2 8 1 0] [ 4 3 5 3] [12 2 8 0]] Segmentation sum tens2: [3 3 9]Utilitaires de séquence
Les utilitaires de séquence incluent des méthodes telles que :
- la fonction argmin, qui renvoie l'index avec la valeur min sur les axes du tenseur d'entrée,
- fonction argmax, qui renvoie l'indice avec la valeur maximale sur les axes du tenseur d'entrée,
- setdiff, qui calcule la différence entre deux listes de nombres ou de chaînes,
- où la fonction, qui renverra des éléments soit à partir de deux éléments passés x ou y, qui dépend de la condition passée, ou
- fonction unique, qui renverra des éléments uniques dans un tenseur 1-D.
Nous démontrons quelques exemples d'exécution ci-dessous :
import numpy as np import tensorflow as tf def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) x = convert(np.array([ [2, 2, 1, 3], [4, 5, 6, -1], [0, 1, 1, -2], [6, 2, 3, 0] ])) y = convert(np.array([1, 2, 5, 3, 7])) z = convert(np.array([1, 0, 4, 6, 2])) arg_min = tf.argmin(x, 1) arg_max = tf.argmax(x, 1) unique = tf.unique(y) diff = tf.setdiff1d(y, z) with tf.Session() as session: print "Argmin = ", session.run(arg_min) print "Argmax = ", session.run(arg_max) print "Unique_values = ", session.run(unique)[0] print "Unique_idx = ", session.run(unique)[1] print "Setdiff_values = ", session.run(diff)[0] print "Setdiff_idx = ", session.run(diff)[1] print session.run(diff)[1]Sortir:
Argmin = [2 3 3 3] Argmax = [3 2 1 0] Unique_values = [ 1. 2. 5. 3. 7.] Unique_idx = [0 1 2 3 4] Setdiff_values = [ 5. 3. 7.] Setdiff_idx = [2 3 4]Apprentissage automatique avec TensorFlow
Dans cette section, nous allons présenter un cas d'utilisation de machine learning avec TensorFlow. Le premier exemple sera un algorithme de classification des données avec l'approche kNN, et le second utilisera l'algorithme de régression linéaire.
kNN
Le premier algorithme est k-Nearest Neighbors (kNN). Il s'agit d'un algorithme d'apprentissage supervisé qui utilise des métriques de distance, par exemple la distance euclidienne, pour classer les données par rapport à la formation. C'est l'un des algorithmes les plus simples, mais toujours très puissant pour classer les données. Avantages de cet algorithme :
- Offre une grande précision lorsque le modèle d'entraînement est suffisamment grand et
- N'est généralement pas sensible aux valeurs aberrantes et nous n'avons pas besoin d'hypothèses sur les données.
Inconvénients de cet algorithme :
- Coûteux en calcul, et
- Nécessite beaucoup de mémoire lorsque de nouvelles données classifiées doivent être ajoutées à toutes les instances de formation initiales.
La distance que nous utiliserons dans cet exemple de code est euclidienne, qui définit la distance entre deux points comme ceci :
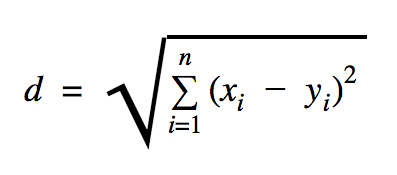
Dans cette formule, n est le nombre de dimensions de l'espace, x est le vecteur des données d'apprentissage et y est un nouveau point de données que nous voulons classer.
import os import numpy as np import tensorflow as tf ccf_train_data = "train_dataset.csv" ccf_test_data = "test_dataset.csv" dataset_dir = os.path.abspath(os.path.join(os.path.dirname(__file__), '../datasets')) ccf_train_filepath = os.path.join(dataset_dir, ccf_train_data) ccf_test_filepath = os.path.join(dataset_dir, ccf_test_data) def load_data(filepath): from numpy import genfromtxt csv_data = genfromtxt(filepath, delimiter=",", skip_header=1) data = [] labels = [] for d in csv_data: data.append(d[:-1]) labels.append(d[-1]) return np.array(data), np.array(labels) train_dataset, train_labels = load_data(ccf_train_filepath) test_dataset, test_labels = load_data(ccf_test_filepath) train_pl = tf.placeholder("float", [None, 28]) test_pl = tf.placeholder("float", [28]) knn_prediction = tf.reduce_sum(tf.abs(tf.add(train_pl, tf.negative(test_pl))), axis=1) pred = tf.argmin(knn_prediction, 0) with tf.Session() as tf_session: missed = 0 for i in xrange(len(test_dataset)): knn_index = tf_session.run(pred, feed_dict={train_pl: train_dataset, test_pl: test_dataset[i]}) print "Predicted class {} -- True class {}".format(train_labels[knn_index], test_labels[i]) if train_labels[knn_index] != test_labels[i]: missed += 1 tf.summary.FileWriter("../samples/article/logs", tf_session.graph) print "Missed: {} -- Total: {}".format(missed, len(test_dataset))L'ensemble de données que nous avons utilisé dans l'exemple ci-dessus est celui qui peut être trouvé dans la section des ensembles de données Kaggle. Nous avons utilisé celui qui contient les transactions effectuées par les cartes de crédit des titulaires européens. Nous utilisons les données sans aucun nettoyage ni filtrage et, conformément à la description de Kaggle pour cet ensemble de données, elles sont très déséquilibrées. Le jeu de données contient 31 variables : Time, V1, …, V28, Amount et Class. Dans cet exemple de code, nous utilisons uniquement V1, …, V28 et Class. La classe étiquette les transactions qui sont frauduleuses avec 1 et celles qui ne le sont pas avec 0.
L'exemple de code contient principalement les choses que nous avons décrites dans les sections précédentes à l'exception où nous avons introduit la fonction de chargement d'un jeu de données. La fonction load_data(filepath) prendra un fichier CSV comme argument et renverra un tuple avec des données et des étiquettes définies dans CSV.
Juste en dessous de cette fonction, nous avons défini des espaces réservés pour le test et les données formées. Les données formées sont utilisées dans le modèle de prédiction pour résoudre les étiquettes des données d'entrée qui doivent être classées. Dans notre cas, kNN utilise la distance euclidienne pour obtenir l'étiquette la plus proche.
Le taux d'erreur peut être calculé par simple division avec le nombre lorsqu'un classificateur a raté le nombre total d'exemples qui, dans notre cas, pour cet ensemble de données est de 0,2 (c'est-à-dire que le classificateur nous donne la mauvaise étiquette de données pour 20 % des données de test).
Régression linéaire
L'algorithme de régression linéaire recherche une relation linéaire entre deux variables. Si nous étiquetons la variable dépendante comme y et la variable indépendante comme x, alors nous essayons d'estimer les paramètres de la fonction y = Wx + b .
La régression linéaire est un algorithme largement utilisé dans le domaine des sciences appliquées. Cet algorithme permet d'ajouter dans l'implémentation deux concepts importants de l'apprentissage automatique : la fonction de coût et la méthode de descente de gradient pour trouver le minimum de la fonction.
Un algorithme d'apprentissage automatique qui est mis en œuvre à l'aide de cette méthode doit prédire les valeurs de y en fonction de x où un algorithme de régression linéaire déterminera les valeurs W et b , qui sont en fait des inconnues et qui sont déterminées tout au long du processus de formation. Une fonction de coût est choisie, et généralement l'erreur quadratique moyenne est utilisée là où la descente de gradient est l'algorithme d'optimisation utilisé pour trouver un minimum local de la fonction de coût.
La méthode de descente de gradient n'est qu'un minimum de fonction locale, mais elle peut être utilisée dans la recherche d'un minimum global en choisissant aléatoirement un nouveau point de départ une fois qu'elle a trouvé un minimum local et en répétant ce processus plusieurs fois. Si le nombre de minima de la fonction est limité et que le nombre de tentatives est très élevé, il y a de fortes chances qu'à un moment donné, le minimum global soit repéré. Nous laisserons quelques détails supplémentaires sur cette technique pour l'article que nous avons mentionné dans la section d'introduction.
import tensorflow as tf import numpy as np test_data_size = 2000 iterations = 10000 learn_rate = 0.005 def generate_test_values(): train_x = [] train_y = [] for _ in xrange(test_data_size): x1 = np.random.rand() x2 = np.random.rand() x3 = np.random.rand() y_f = 2 * x1 + 3 * x2 + 7 * x3 + 4 train_x.append([x1, x2, x3]) train_y.append(y_f) return np.array(train_x), np.transpose([train_y]) x = tf.placeholder(tf.float32, [None, 3], name="x") W = tf.Variable(tf.zeros([3, 1]), name="W") b = tf.Variable(tf.zeros([1]), name="b") y = tf.placeholder(tf.float32, [None, 1]) model = tf.add(tf.matmul(x, W), b) cost = tf.reduce_mean(tf.square(y - model)) train = tf.train.GradientDescentOptimizer(learn_rate).minimize(cost) train_dataset, train_values = generate_test_values() init = tf.global_variables_initializer() with tf.Session() as session: session.run(init) for _ in xrange(iterations): session.run(train, feed_dict={ x: train_dataset, y: train_values }) print "cost = {}".format(session.run(cost, feed_dict={ x: train_dataset, y: train_values })) print "W = {}".format(session.run(W)) print "b = {}".format(session.run(b))Sortir:
cost = 3.1083032809e-05 W = [[ 1.99049103] [ 2.9887135 ] [ 6.98754263]] b = [ 4.01742554] Dans l'exemple ci-dessus, nous avons deux nouvelles variables, que nous avons appelées cost et train . Avec ces deux variables, nous avons défini un optimiseur que nous voulons utiliser dans notre modèle d'apprentissage et la fonction que nous voulons minimiser.
A la fin, les paramètres de sortie de W et b doivent être identiques à ceux définis dans la fonction generate_test_values . À la ligne 17, nous avons en fait défini une fonction que nous avons utilisée pour générer les points de données linéaires à entraîner où w1=2 , w2=3 , w3=7 et b=4 . La régression linéaire de l'exemple ci-dessus est multivariée où plus d'une variable indépendante est utilisée.
Conclusion
Comme vous pouvez le voir dans ce didacticiel TensorFlow, TensorFlow est un cadre puissant qui facilite l'utilisation d'expressions mathématiques et de tableaux multidimensionnels, ce qui est fondamentalement nécessaire dans l'apprentissage automatique. Il élimine également les complexités de l'exécution des graphiques de données et de la mise à l'échelle.
Au fil du temps, TensorFlow a gagné en popularité et est maintenant utilisé par les développeurs pour résoudre des problèmes à l'aide de méthodes d'apprentissage en profondeur pour la reconnaissance d'images, la détection de vidéos, le traitement de texte comme l'analyse des sentiments, etc. Comme toute autre bibliothèque, vous aurez peut-être besoin d'un certain temps pour vous habituer. aux concepts sur lesquels TensorFlow est construit. Et, une fois que vous l'avez fait, avec l'aide de la documentation et de l'assistance de la communauté, représenter les problèmes sous forme de graphiques de données et les résoudre avec TensorFlow peut rendre l'apprentissage automatique à grande échelle un processus moins fastidieux.
