Primeros pasos con TensorFlow: un tutorial de aprendizaje automático
Publicado: 2022-03-11TensorFlow es una biblioteca de software de código abierto creada por Google que se utiliza para implementar sistemas de aprendizaje automático y aprendizaje profundo. Estos dos nombres contienen una serie de poderosos algoritmos que comparten un desafío común: permitir que una computadora aprenda cómo detectar automáticamente patrones complejos y/o tomar las mejores decisiones posibles.
Si está interesado en los detalles sobre estos sistemas, puede obtener más información en las publicaciones del blog de Toptal sobre aprendizaje automático y aprendizaje profundo.
TensorFlow, en esencia, es una biblioteca para la programación de flujo de datos. Aprovecha varias técnicas de optimización para hacer que el cálculo de expresiones matemáticas sea más fácil y eficiente.
Algunas de las características clave de TensorFlow son:
- Funciona eficientemente con expresiones matemáticas que involucran matrices multidimensionales.
- Buen soporte de redes neuronales profundas y conceptos de aprendizaje automático.
- Computación GPU/CPU donde se puede ejecutar el mismo código en ambas arquitecturas
- Alta escalabilidad de computación a través de máquinas y grandes conjuntos de datos
Juntas, estas características hacen de TensorFlow el marco perfecto para la inteligencia artificial a escala de producción.
En este tutorial de TensorFlow, aprenderá cómo puede usar métodos de aprendizaje automático simples pero potentes en TensorFlow y cómo puede usar algunas de sus bibliotecas auxiliares para depurar, visualizar y modificar los modelos creados con él.
Instalación de TensorFlow
Usaremos la API Python de TensorFlow, que funciona con Python 2.7 y Python 3.3+. La versión GPU (solo Linux) requiere Cuda Toolkit 7.0+ y cuDNN v2+.
Usaremos el sistema de administración de dependencias del paquete Conda para instalar TensorFlow. Conda nos permite separar múltiples entornos en una máquina. Puede aprender cómo instalar Conda desde aquí.
Después de instalar Conda, podemos crear el entorno que usaremos para la instalación y el uso de TensorFlow. El siguiente comando creará nuestro entorno con algunas bibliotecas adicionales como NumPy, que es muy útil una vez que comenzamos a usar TensorFlow.
La versión de Python instalada dentro de este entorno es 2.7 y usaremos esta versión en este artículo.
conda create --name TensorflowEnv biopython Para facilitar las cosas, estamos instalando biopython aquí en lugar de solo NumPy. Esto incluye NumPy y algunos otros paquetes que necesitaremos. Siempre puede instalar los paquetes a medida que los necesite utilizando los conda install o pip install .
El siguiente comando activará el entorno Conda creado. Podremos usar paquetes instalados dentro de él, sin mezclarlos con paquetes que están instalados globalmente o en algunos otros entornos.
source activate TensorFlowEnvLa herramienta de instalación de pip es una parte estándar de un entorno Conda. Lo usaremos para instalar la biblioteca TensorFlow. Antes de hacer eso, un buen primer paso es actualizar pip a la última versión, usando el siguiente comando:
pip install --upgrade pipAhora estamos listos para instalar TensorFlow, ejecutando:
pip install tensorflowLa descarga y compilación de TensorFlow puede demorar varios minutos. Al momento de escribir, esto instala TensorFlow 1.1.0.
Gráficos de flujo de datos
En TensorFlow, el cálculo se describe mediante gráficos de flujo de datos. Cada nodo del gráfico representa una instancia de una operación matemática (como suma, división o multiplicación) y cada borde es un conjunto de datos multidimensional (tensor) en el que se realizan las operaciones.
Como TensorFlow funciona con gráficos computacionales, se administran donde cada nodo representa la instanciación de una operación donde cada operación tiene cero o más entradas y cero o más salidas.
Los bordes en TensorFlow se pueden agrupar en dos categorías: Los bordes normales transfieren la estructura de datos (tensores) donde es posible que la salida de una operación se convierta en la entrada de otra operación y los bordes especiales, que se usan para controlar la dependencia entre dos nodos para establecer la orden de operación donde un nodo espera a que otro termine.
Expresiones simples
Antes de pasar a discutir los elementos de TensorFlow, primero haremos una sesión de trabajo con TensorFlow, para tener una idea de cómo se ve un programa de TensorFlow.
Comencemos con expresiones simples y supongamos que, por alguna razón, queremos evaluar la función y = 5*x + 13 al estilo de TensorFlow.
En código Python simple, se vería así:
x = -2.0 y = 5*x + 13 print ylo que nos da en este caso un resultado de 3.0.
Ahora convertiremos la expresión anterior en términos de TensorFlow.
constantes
En TensorFlow, las constantes se crean mediante la función constant, que tiene la firma constant(value, dtype=None, shape=None, name='Const', verify_shape=False) , donde value es un valor constante real que se usará en dtype es el parámetro del tipo de datos (p. ej., float32/64, int8/16, etc.), la shape son las dimensiones opcionales, el name es un nombre opcional para el tensor y el último parámetro es un valor booleano que indica la verificación del forma de valores.
Si necesita constantes con valores específicos dentro de su modelo de entrenamiento, entonces el objeto constant se puede usar como en el siguiente ejemplo:
z = tf.constant(5.2, name="x", dtype=tf.float32)Variables
Las variables en TensorFlow son búferes en memoria que contienen tensores que deben inicializarse explícitamente y usarse en el gráfico para mantener el estado durante la sesión. Simplemente llamando al constructor, la variable se agrega en el gráfico computacional.
Las variables son especialmente útiles una vez que comienza con los modelos de entrenamiento y se usan para mantener y actualizar parámetros. Un valor inicial pasado como argumento de un constructor representa un tensor u objeto que se puede convertir o devolver como tensor. Eso significa que si queremos llenar una variable con algunos valores predefinidos o aleatorios para usar luego en el proceso de entrenamiento y actualizarlos en iteraciones, podemos definirla de la siguiente manera:
k = tf.Variable(tf.zeros([1]), name="k")Otra forma de usar variables en TensorFlow es en cálculos donde esa variable no se puede entrenar y se puede definir de la siguiente manera:
k = tf.Variable(tf.add(a, b), trainable=False)Sesiones
Para evaluar realmente los nodos, debemos ejecutar un gráfico computacional dentro de una sesión.
Una sesión encapsula el control y el estado del tiempo de ejecución de TensorFlow. Una sesión sin parámetros usará el gráfico predeterminado creado en la sesión actual, de lo contrario, la clase de sesión acepta un parámetro de gráfico, que se usa en esa sesión para ejecutarse.
A continuación se incluye un breve fragmento de código que muestra cómo se pueden usar los términos definidos anteriormente en TensorFlow para calcular una función lineal simple.
import tensorflow as tf x = tf.constant(-2.0, name="x", dtype=tf.float32) a = tf.constant(5.0, name="a", dtype=tf.float32) b = tf.constant(13.0, name="b", dtype=tf.float32) y = tf.Variable(tf.add(tf.multiply(a, x), b)) init = tf.global_variables_initializer() with tf.Session() as session: session.run(init) print session.run(y)Uso de TensorFlow: definición de gráficos computacionales
Lo bueno de trabajar con gráficos de flujo de datos es que el modelo de ejecución está separado de su ejecución (en CPU, GPU o alguna combinación) donde, una vez implementado, el software en TensorFlow se puede usar en la CPU o GPU donde toda la complejidad relacionada con el código la ejecución está oculta.
El gráfico de cálculo se puede construir en el proceso de usar la biblioteca TensorFlow sin tener que instanciar explícitamente los objetos Graph.
Se puede crear un objeto Graph en TensorFlow como resultado de una simple línea de código como c = tf.add(a, b) . Esto creará un nodo de operación que toma dos tensores a y b que producen su suma c como salida.
El gráfico de cálculo es un proceso integrado que utiliza la biblioteca sin necesidad de llamar directamente al objeto gráfico. Un objeto de gráfico en TensorFlow, que contiene un conjunto de operaciones y tensores como unidades de datos, se usa entre operaciones que permite el mismo proceso y contiene más de un gráfico donde cada gráfico se asignará a una sesión diferente. Por ejemplo, la simple línea de código c = tf.add(a, b) creará un nodo de operación que toma dos tensores a y b como entrada y produce su suma c como salida.
TensorFlow también proporciona un mecanismo de alimentación para parchear un tensor a cualquier operación en el gráfico, donde la alimentación reemplaza la salida de una operación con el valor del tensor. Los datos del feed se pasan como un argumento en la llamada a la función run() .
Un marcador de posición es la forma en que TensorFlow permite a los desarrolladores inyectar datos en el gráfico de cálculo a través de marcadores de posición que están vinculados dentro de algunas expresiones. La firma del marcador de posición es:
placeholder(dtype, shape=None, name=None)donde dtype es el tipo de elementos en los tensores y puede proporcionar tanto la forma de los tensores que se alimentarán como el nombre de la operación.
Si no se pasa la forma, este tensor se puede alimentar con cualquier forma. Una nota importante es que el tensor de marcador de posición tiene que ser alimentado con datos, de lo contrario, al ejecutar la sesión y si falta esa parte, el marcador de posición genera un error con la siguiente estructura:
InvalidArgumentError (see above for traceback): You must feed a value for placeholder tensor 'y' with dtype floatLa ventaja de los marcadores de posición es que permiten a los desarrolladores crear operaciones y el gráfico computacional en general, sin necesidad de proporcionar los datos por adelantado para eso, y los datos se pueden agregar en tiempo de ejecución desde fuentes externas.
Tomemos un problema simple de multiplicar dos números enteros x e y al estilo de TensorFlow, donde se usará un marcador de posición junto con un mecanismo de alimentación a través del método run de la sesión.
import tensorflow as tf x = tf.placeholder(tf.float32, name="x") y = tf.placeholder(tf.float32, name="y") z = tf.multiply(x, y, name="z") with tf.Session() as session: print session.run(z, feed_dict={x: 2.1, y: 3.0})Visualización del gráfico computacional con TensorBoard
TensorBoard es una herramienta de visualización para analizar gráficos de flujo de datos. Esto puede ser útil para obtener una mejor comprensión de los modelos de aprendizaje automático.
Con TensorBoard, puede obtener información sobre diferentes tipos de estadísticas sobre los parámetros y detalles sobre las partes del gráfico computacional en general. No es inusual que una red neuronal profunda tenga una gran cantidad de nodos. TensorBoard permite a los desarrolladores obtener información sobre cada nodo y cómo se ejecuta el cálculo en el tiempo de ejecución de TensorFlow.
Ahora volvamos a nuestro ejemplo del comienzo de este tutorial de TensorFlow donde definimos una función lineal con el formato y = a*x + b .
Para registrar eventos de la sesión que luego se pueden usar en TensorBoard, TensorFlow proporciona la clase FileWriter . Se puede usar para crear un archivo de eventos para almacenar resúmenes donde el constructor acepta seis parámetros y se ve así:
__init__(logdir, graph=None, max_queue=10, flush_secs=120, graph_def=None, filename_suffix=None)donde se requiere el parámetro logdir, y otros tienen valores predeterminados. El parámetro gráfico se pasará desde el objeto de sesión creado en el programa de entrenamiento. El código de ejemplo completo se ve así:
import tensorflow as tf x = tf.constant(-2.0, name="x", dtype=tf.float32) a = tf.constant(5.0, name="a", dtype=tf.float32) b = tf.constant(13.0, name="b", dtype=tf.float32) y = tf.Variable(tf.add(tf.multiply(a, x), b)) init = tf.global_variables_initializer() with tf.Session() as session: merged = tf.summary.merge_all() // new writer = tf.summary.FileWriter("logs", session.graph) // new session.run(init) print session.run(y) Agregamos solo dos líneas nuevas. Fusionamos todos los resúmenes recopilados en el gráfico predeterminado y FileWriter se usa para volcar eventos en el archivo como describimos anteriormente, respectivamente.
Luego de ejecutar el programa, tenemos el archivo en el directorio logs, y el último paso es ejecutar tensorboard :
tensorboard --logdir logs/ Ahora TensorBoard se inicia y se ejecuta en el puerto predeterminado 6006. Después de abrir http://localhost:6006 y hacer clic en el elemento del menú Gráficos (ubicado en la parte superior de la página), podrá ver el gráfico, como el en la imagen de abajo:
TensorBoard marca las constantes y los símbolos específicos de los nodos de resumen, que se describen a continuación.
Matemáticas con TensorFlow
Los tensores son las estructuras de datos básicas en TensorFlow y representan los bordes de conexión en un gráfico de flujo de datos.
Un tensor simplemente identifica una matriz o lista multidimensional. La estructura tensorial se puede identificar con tres parámetros: rango, forma y tipo.
- Rango: Identifica el número de dimensiones del tensor. Un rango se conoce como el orden o n-dimensiones de un tensor, donde, por ejemplo, el tensor de rango 1 es un vector o el tensor de rango 2 es una matriz.
- Forma: La forma de un tensor es el número de filas y columnas que tiene.
- Tipo: el tipo de datos asignado a los elementos tensoriales.
Para construir un tensor en TensorFlow, podemos construir una matriz de n dimensiones. Esto se puede hacer fácilmente usando la biblioteca NumPy o convirtiendo una matriz n-dimensional de Python en un tensor TensorFlow.
Para construir un tensor 1-d, usaremos una matriz NumPy, que construiremos pasando una lista de Python incorporada.
import numpy as np tensor_1d = np.array([1.45, -1, 0.2, 102.1])Trabajar con este tipo de matriz es similar a trabajar con una lista de Python integrada. La principal diferencia es que la matriz NumPy también contiene algunas propiedades adicionales, como dimensión, forma y tipo.
> > print tensor1d [ 1.45 -1. 0.2 102.1 ] > > print tensor1d[0] 1.45 > > print tensor1d[2] 0.2 > > print tensor1d.ndim 1 > > print tensor1d.shape (4,) > > print tensor1d.dtype float64Una matriz NumPy se puede convertir fácilmente en un tensor de TensorFlow con la función auxiliar convert_to_tensor, que ayuda a los desarrolladores a convertir objetos de Python en objetos de tensor. Esta función acepta objetos de tensor, matrices NumPy, listas de Python y escalares de Python.
tensor = tf.convert_to_tensor(tensor_1d, dtype=tf.float64)Ahora, si vinculamos nuestro tensor a la sesión de TensorFlow, podremos ver los resultados de nuestra conversión.
tensor = tf.convert_to_tensor(tensor_1d, dtype=tf.float64) with tf.Session() as session: print session.run(tensor) print session.run(tensor[0]) print session.run(tensor[1])Producción:
[ 1.45 -1. 0.2 102.1 ] 1.45 -1.0Podemos crear un tensor o matriz bidimensional de manera similar:
tensor_2d = np.array(np.random.rand(4, 4), dtype='float32') tensor_2d_1 = np.array(np.random.rand(4, 4), dtype='float32') tensor_2d_2 = np.array(np.random.rand(4, 4), dtype='float32') m1 = tf.convert_to_tensor(tensor_2d) m2 = tf.convert_to_tensor(tensor_2d_1) m3 = tf.convert_to_tensor(tensor_2d_2) mat_product = tf.matmul(m1, m2) mat_sum = tf.add(m2, m3) mat_det = tf.matrix_determinant(m3) with tf.Session() as session: print session.run(mat_product) print session.run(mat_sum) print session.run(mat_det)Operaciones de tensor
En el ejemplo anterior, presentamos algunas operaciones de TensorFlow en los vectores y matrices. Las operaciones realizan ciertos cálculos sobre los tensores. Los cálculos que son se muestran en la siguiente tabla.
| Operador TensorFlow | Descripción |
|---|---|
| tf.añadir | x+y |
| tf.restar | xy |
| tf.multiplicar | x*y |
| tf.div | x/y |
| tf.mod | x % y |
| tf.abs | |x| |
| tf.negativo | -X |
| tf.signo | signo(x) |
| tf.cuadrado | x*x |
| tf.redondo | redondo(x) |
| tf.sqrt | sqrt(x) |
| tf.pow | x^y |
| tf.exp | e ^ x |
| tf.log | registro (x) |
| tf.máximo | máx(x, y) |
| tf.mínimo | min(x, y) |
| tf.cos | porque(x) |
| tf.pecado | pecado(x) |
Las operaciones de TensorFlow enumeradas en la tabla anterior funcionan con objetos de tensor y se realizan por elementos. Entonces, si desea calcular el coseno para un vector x, la operación TensorFlow hará cálculos para cada elemento en el tensor pasado.

tensor_1d = np.array([0, 0, 0]) tensor = tf.convert_to_tensor(tensor_1d, dtype=tf.float64) with tf.Session() as session: print session.run(tf.cos(tensor))Producción:
[ 1. 1. 1.]Operaciones Matriciales
Las operaciones matriciales son muy importantes para los modelos de aprendizaje automático, como la regresión lineal, ya que a menudo se usan en ellos. TensorFlow es compatible con todas las operaciones matriciales más comunes, como la multiplicación, la transposición, la inversión, el cálculo del determinante, la resolución de ecuaciones lineales y muchas más.
A continuación, explicaremos algunas de las operaciones matriciales. Tienden a ser importantes cuando se trata de modelos de aprendizaje automático, como en la regresión lineal. Escribamos un código que realice operaciones básicas con matrices como la multiplicación, la transposición, el determinante, la multiplicación, sol y muchas más.
A continuación se muestran ejemplos básicos de cómo llamar a estas operaciones.
import tensorflow as tf import numpy as np def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) m1 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m2 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m3 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m4 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m5 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m_tranpose = tf.transpose(m1) m_mul = tf.matmul(m1, m2) m_det = tf.matrix_determinant(m3) m_inv = tf.matrix_inverse(m4) m_solve = tf.matrix_solve(m5, [[1], [1], [1], [1]]) with tf.Session() as session: print session.run(m_tranpose) print session.run(m_mul) print session.run(m_inv) print session.run(m_det) print session.run(m_solve)Transformación de datos
Reducción
TensorFlow admite diferentes tipos de reducción. La reducción es una operación que elimina una o más dimensiones de un tensor realizando ciertas operaciones en esas dimensiones. Puede encontrar una lista de reducciones admitidas para la versión actual de TensorFlow aquí. Presentaremos algunos de ellos en el siguiente ejemplo.
import tensorflow as tf import numpy as np def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) x = convert( np.array( [ (1, 2, 3), (4, 5, 6), (7, 8, 9) ]), tf.int32) bool_tensor = convert([(True, False, True), (False, False, True), (True, False, False)], tf.bool) red_sum_0 = tf.reduce_sum(x) red_sum = tf.reduce_sum(x, axis=1) red_prod_0 = tf.reduce_prod(x) red_prod = tf.reduce_prod(x, axis=1) red_min_0 = tf.reduce_min(x) red_min = tf.reduce_min(x, axis=1) red_max_0 = tf.reduce_max(x) red_max = tf.reduce_max(x, axis=1) red_mean_0 = tf.reduce_mean(x) red_mean = tf.reduce_mean(x, axis=1) red_bool_all_0 = tf.reduce_all(bool_tensor) red_bool_all = tf.reduce_all(bool_tensor, axis=1) red_bool_any_0 = tf.reduce_any(bool_tensor) red_bool_any = tf.reduce_any(bool_tensor, axis=1) with tf.Session() as session: print "Reduce sum without passed axis parameter: ", session.run(red_sum_0) print "Reduce sum with passed axis=1: ", session.run(red_sum) print "Reduce product without passed axis parameter: ", session.run(red_prod_0) print "Reduce product with passed axis=1: ", session.run(red_prod) print "Reduce min without passed axis parameter: ", session.run(red_min_0) print "Reduce min with passed axis=1: ", session.run(red_min) print "Reduce max without passed axis parameter: ", session.run(red_max_0) print "Reduce max with passed axis=1: ", session.run(red_max) print "Reduce mean without passed axis parameter: ", session.run(red_mean_0) print "Reduce mean with passed axis=1: ", session.run(red_mean) print "Reduce bool all without passed axis parameter: ", session.run(red_bool_all_0) print "Reduce bool all with passed axis=1: ", session.run(red_bool_all) print "Reduce bool any without passed axis parameter: ", session.run(red_bool_any_0) print "Reduce bool any with passed axis=1: ", session.run(red_bool_any)Producción:
Reduce sum without passed axis parameter: 45 Reduce sum with passed axis=1: [ 6 15 24] Reduce product without passed axis parameter: 362880 Reduce product with passed axis=1: [ 6 120 504] Reduce min without passed axis parameter: 1 Reduce min with passed axis=1: [1 4 7] Reduce max without passed axis parameter: 9 Reduce max with passed axis=1: [3 6 9] Reduce mean without passed axis parameter: 5 Reduce mean with passed axis=1: [2 5 8] Reduce bool all without passed axis parameter: False Reduce bool all with passed axis=1: [False False False] Reduce bool any without passed axis parameter: True Reduce bool any with passed axis=1: [ True True True]El primer parámetro de los operadores de reducción es el tensor que queremos reducir. El segundo parámetro son los índices de dimensiones a lo largo de los cuales queremos realizar la reducción. Ese parámetro es opcional y, si no se pasa, la reducción se realizará en todas las dimensiones.
Podemos echar un vistazo a la operación reduce_sum. Pasamos un tensor 2-d y queremos reducirlo a lo largo de la dimensión 1.
En nuestro caso, la suma resultante sería:
[1 + 2 + 3 = 6, 4 + 5 + 6 = 15, 7 + 8 + 9 = 24]Si pasamos la dimensión 0, el resultado sería:
[1 + 4 + 7 = 12, 2 + 5 + 8 = 15, 3 + 6 + 9 = 18]Si no pasamos ningún eje, el resultado es solo la suma total de:
1 + 4 + 7 = 12, 2 + 5 + 8 = 15, 3 + 6 + 9 = 45Todas las funciones de reducción tienen una interfaz similar y se enumeran en la documentación de reducción de TensorFlow.
Segmentación
La segmentación es un proceso en el que una de las dimensiones es el proceso de asignar dimensiones a índices de segmento proporcionados, y los elementos resultantes están determinados por una fila de índice.
La segmentación es en realidad agrupar los elementos bajo índices repetidos, por ejemplo, en nuestro caso, tenemos identificadores segmentados [0, 0, 1, 2, 2] aplicados en el tensor tens1 , lo que significa que la primera y la segunda matriz se transformarán después de la segmentación operación (en nuestro caso suma) y obtendrá una nueva matriz, que se parece a (2, 8, 1, 0) = (2+0, 5+3, 3-2, -5+5) . El tercer elemento en el tensor tens1 no se modifica porque no está agrupado en ningún índice repetido, y las últimas dos matrices se suman de la misma manera que en el caso del primer grupo. Además de la suma, TensorFlow admite el producto, la media, el máximo y el mínimo.
import tensorflow as tf import numpy as np def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) seg_ids = tf.constant([0, 0, 1, 2, 2]) tens1 = convert(np.array([(2, 5, 3, -5), (0, 3, -2, 5), (4, 3, 5, 3), (6, 1, 4, 0), (6, 1, 4, 0)]), tf.int32) tens2 = convert(np.array([1, 2, 3, 4, 5]), tf.int32) seg_sum = tf.segment_sum(tens1, seg_ids) seg_sum_1 = tf.segment_sum(tens2, seg_ids) with tf.Session() as session: print "Segmentation sum tens1: ", session.run(seg_sum) print "Segmentation sum tens2: ", session.run(seg_sum_1) Segmentation sum tens1: [[ 2 8 1 0] [ 4 3 5 3] [12 2 8 0]] Segmentation sum tens2: [3 3 9]Utilidades de secuencia
Las utilidades de secuencia incluyen métodos como:
- función argmin, que devuelve el índice con valor mínimo en los ejes del tensor de entrada,
- función argmax, que devuelve el índice con el valor máximo en los ejes del tensor de entrada,
- setdiff, que calcula la diferencia entre dos listas de números o cadenas,
- where función, que devolverá elementos de dos elementos pasados x o y, que depende de la condición pasada, o
- función única, que devolverá elementos únicos en un tensor 1-D.
Demostramos algunos ejemplos de ejecución a continuación:
import numpy as np import tensorflow as tf def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) x = convert(np.array([ [2, 2, 1, 3], [4, 5, 6, -1], [0, 1, 1, -2], [6, 2, 3, 0] ])) y = convert(np.array([1, 2, 5, 3, 7])) z = convert(np.array([1, 0, 4, 6, 2])) arg_min = tf.argmin(x, 1) arg_max = tf.argmax(x, 1) unique = tf.unique(y) diff = tf.setdiff1d(y, z) with tf.Session() as session: print "Argmin = ", session.run(arg_min) print "Argmax = ", session.run(arg_max) print "Unique_values = ", session.run(unique)[0] print "Unique_idx = ", session.run(unique)[1] print "Setdiff_values = ", session.run(diff)[0] print "Setdiff_idx = ", session.run(diff)[1] print session.run(diff)[1]Producción:
Argmin = [2 3 3 3] Argmax = [3 2 1 0] Unique_values = [ 1. 2. 5. 3. 7.] Unique_idx = [0 1 2 3 4] Setdiff_values = [ 5. 3. 7.] Setdiff_idx = [2 3 4]Aprendizaje automático con TensorFlow
En esta sección, presentaremos un caso de uso de aprendizaje automático con TensorFlow. El primer ejemplo será un algoritmo para clasificar datos con el enfoque kNN, y el segundo usará el algoritmo de regresión lineal.
kNN
El primer algoritmo es k-vecinos más cercanos (kNN). Es un algoritmo de aprendizaje supervisado que utiliza métricas de distancia, por ejemplo, la distancia euclidiana, para clasificar los datos contra el entrenamiento. Es uno de los algoritmos más simples, pero aún así realmente poderoso para clasificar datos. Pros de este algoritmo:
- Da alta precisión cuando el modelo de entrenamiento es lo suficientemente grande, y
- Por lo general, no es sensible a los valores atípicos, y no necesitamos hacer suposiciones sobre los datos.
Contras de este algoritmo:
- Computacionalmente caro, y
- Requiere mucha memoria donde se deben agregar nuevos datos clasificados a todas las instancias de capacitación inicial.
La distancia que usaremos en este ejemplo de código es euclidiana, que define la distancia entre dos puntos de esta manera:
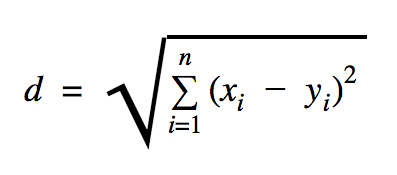
En esta fórmula, n es el número de dimensiones del espacio, x es el vector de los datos de entrenamiento e y es un nuevo punto de datos que queremos clasificar.
import os import numpy as np import tensorflow as tf ccf_train_data = "train_dataset.csv" ccf_test_data = "test_dataset.csv" dataset_dir = os.path.abspath(os.path.join(os.path.dirname(__file__), '../datasets')) ccf_train_filepath = os.path.join(dataset_dir, ccf_train_data) ccf_test_filepath = os.path.join(dataset_dir, ccf_test_data) def load_data(filepath): from numpy import genfromtxt csv_data = genfromtxt(filepath, delimiter=",", skip_header=1) data = [] labels = [] for d in csv_data: data.append(d[:-1]) labels.append(d[-1]) return np.array(data), np.array(labels) train_dataset, train_labels = load_data(ccf_train_filepath) test_dataset, test_labels = load_data(ccf_test_filepath) train_pl = tf.placeholder("float", [None, 28]) test_pl = tf.placeholder("float", [28]) knn_prediction = tf.reduce_sum(tf.abs(tf.add(train_pl, tf.negative(test_pl))), axis=1) pred = tf.argmin(knn_prediction, 0) with tf.Session() as tf_session: missed = 0 for i in xrange(len(test_dataset)): knn_index = tf_session.run(pred, feed_dict={train_pl: train_dataset, test_pl: test_dataset[i]}) print "Predicted class {} -- True class {}".format(train_labels[knn_index], test_labels[i]) if train_labels[knn_index] != test_labels[i]: missed += 1 tf.summary.FileWriter("../samples/article/logs", tf_session.graph) print "Missed: {} -- Total: {}".format(missed, len(test_dataset))El conjunto de datos que usamos en el ejemplo anterior se encuentra en la sección de conjuntos de datos de Kaggle. Usamos el que contiene transacciones realizadas con tarjetas de crédito de titulares europeos. Estamos utilizando los datos sin ninguna limpieza o filtrado y, según la descripción en Kaggle para este conjunto de datos, está muy desequilibrado. El conjunto de datos contiene 31 variables: Tiempo, V1, …, V28, Cantidad y Clase. En este ejemplo de código, usamos solo V1, …, V28 y Class. Class etiqueta las transacciones que son fraudulentas con 1 y las que no lo son con 0.
El ejemplo de código contiene principalmente las cosas que describimos en las secciones anteriores, con la excepción de que presentamos la función para cargar un conjunto de datos. La función load_data(filepath) tomará un archivo CSV como argumento y devolverá una tupla con datos y etiquetas definidas en CSV.
Justo debajo de esa función, hemos definido marcadores de posición para la prueba y datos entrenados. Los datos entrenados se utilizan en el modelo de predicción para resolver las etiquetas de los datos de entrada que deben clasificarse. En nuestro caso, kNN usa la distancia euclidiana para obtener la etiqueta más cercana.
La tasa de error se puede calcular mediante una simple división con el número cuando un clasificador se perdió por el número total de ejemplos que, en nuestro caso, para este conjunto de datos es 0.2 (es decir, el clasificador nos da la etiqueta de datos incorrecta para el 20 % de los datos de prueba).
Regresión lineal
El algoritmo de regresión lineal busca una relación lineal entre dos variables. Si etiquetamos la variable dependiente como y, y la variable independiente como x, entonces estamos tratando de estimar los parámetros de la función y = Wx + b .
La regresión lineal es un algoritmo ampliamente utilizado en el campo de las ciencias aplicadas. Este algoritmo permite agregar en la implementación dos conceptos importantes de aprendizaje automático: la función de costo y el método de descenso de gradiente para encontrar el mínimo de la función.
Un algoritmo de aprendizaje automático que se implementa con este método debe predecir los valores de y en función de x , donde un algoritmo de regresión lineal determinará los valores W y b , que en realidad son desconocidos y se determinan a lo largo del proceso de entrenamiento. Se elige una función de costo y, por lo general, se usa el error cuadrático medio donde el descenso del gradiente es el algoritmo de optimización que se usa para encontrar un mínimo local de la función de costo.
El método de descenso de gradiente es solo un mínimo de función local, pero se puede usar en la búsqueda de un mínimo global eligiendo aleatoriamente un nuevo punto de inicio una vez que haya encontrado un mínimo local y repitiendo este proceso muchas veces. Si el número de mínimos de la función es limitado y hay un número muy alto de intentos, entonces hay una buena posibilidad de que en algún momento se detecte el mínimo global. Dejaremos algunos detalles más sobre esta técnica para el artículo que mencionamos en la sección de introducción.
import tensorflow as tf import numpy as np test_data_size = 2000 iterations = 10000 learn_rate = 0.005 def generate_test_values(): train_x = [] train_y = [] for _ in xrange(test_data_size): x1 = np.random.rand() x2 = np.random.rand() x3 = np.random.rand() y_f = 2 * x1 + 3 * x2 + 7 * x3 + 4 train_x.append([x1, x2, x3]) train_y.append(y_f) return np.array(train_x), np.transpose([train_y]) x = tf.placeholder(tf.float32, [None, 3], name="x") W = tf.Variable(tf.zeros([3, 1]), name="W") b = tf.Variable(tf.zeros([1]), name="b") y = tf.placeholder(tf.float32, [None, 1]) model = tf.add(tf.matmul(x, W), b) cost = tf.reduce_mean(tf.square(y - model)) train = tf.train.GradientDescentOptimizer(learn_rate).minimize(cost) train_dataset, train_values = generate_test_values() init = tf.global_variables_initializer() with tf.Session() as session: session.run(init) for _ in xrange(iterations): session.run(train, feed_dict={ x: train_dataset, y: train_values }) print "cost = {}".format(session.run(cost, feed_dict={ x: train_dataset, y: train_values })) print "W = {}".format(session.run(W)) print "b = {}".format(session.run(b))Producción:
cost = 3.1083032809e-05 W = [[ 1.99049103] [ 2.9887135 ] [ 6.98754263]] b = [ 4.01742554] En el ejemplo anterior, tenemos dos nuevas variables, a las que llamamos cost y train . Con esas dos variables, definimos un optimizador que queremos usar en nuestro modelo de entrenamiento y la función que queremos minimizar.
Al final, los parámetros de salida de W y b deben ser idénticos a los definidos en la función generate_test_values . En la línea 17, en realidad definimos una función que usamos para generar los puntos de datos lineales para entrenar donde w1=2 , w2=3 , w3=7 y b=4 . La regresión lineal del ejemplo anterior es multivariante donde se usa más de una variable independiente.
Conclusión
Como puede ver en este tutorial de TensorFlow, TensorFlow es un marco poderoso que hace que trabajar con expresiones matemáticas y arreglos multidimensionales sea pan comido, algo fundamentalmente necesario en el aprendizaje automático. También abstrae las complejidades de ejecutar los gráficos de datos y escalar.
Con el tiempo, TensorFlow ha ganado popularidad y ahora los desarrolladores lo utilizan para resolver problemas utilizando métodos de aprendizaje profundo para reconocimiento de imágenes, detección de video, procesamiento de texto como análisis de sentimientos, etc. Como cualquier otra biblioteca, es posible que necesite algo de tiempo para acostumbrarse. a los conceptos sobre los que se basa TensorFlow. Y, una vez que lo haga, con la ayuda de la documentación y el apoyo de la comunidad, representar los problemas como gráficos de datos y resolverlos con TensorFlow puede hacer que el aprendizaje automático a escala sea un proceso menos tedioso.
