TensorFlow 入门:机器学习教程
已发表: 2022-03-11TensorFlow 是谷歌创建的一个开源软件库,用于实现机器学习和深度学习系统。 这两个名称包含一系列功能强大的算法,它们具有共同的挑战——允许计算机学习如何自动发现复杂模式和/或做出最佳决策。
如果您对这些系统的详细信息感兴趣,可以从关于机器学习和深度学习的 Toptal 博客文章中了解更多信息。
TensorFlow 的核心是数据流编程库。 它利用各种优化技术使数学表达式的计算更容易和更高效。
TensorFlow 的一些关键特性包括:
- 有效地处理涉及多维数组的数学表达式
- 对深度神经网络和机器学习概念的良好支持
- GPU/CPU 计算可以在两种架构上执行相同的代码
- 跨机器计算和海量数据集的高可扩展性
这些功能共同使 TensorFlow 成为生产规模的机器智能的完美框架。
在本 TensorFlow 教程中,您将了解如何在 TensorFlow 中使用简单而强大的机器学习方法,以及如何使用它的一些辅助库来调试、可视化和调整使用它创建的模型。
安装 TensorFlow
我们将使用 TensorFlow Python API,它适用于 Python 2.7 和 Python 3.3+。 GPU 版本(仅限 Linux)需要 Cuda Toolkit 7.0+ 和 cuDNN v2+。
我们将使用 Conda 包依赖管理系统来安装 TensorFlow。 Conda 允许我们在一台机器上分离多个环境。 您可以从此处了解如何安装 Conda。
安装 Conda 后,我们可以创建用于 TensorFlow 安装和使用的环境。 以下命令将使用一些额外的库(如 NumPy)创建我们的环境,一旦我们开始使用 TensorFlow,这将非常有用。
这个环境里面安装的Python版本是2.7,我们将在本文中使用这个版本。
conda create --name TensorflowEnv biopython 为了方便起见,我们在这里安装 biopython 而不仅仅是 NumPy。 这包括 NumPy 和我们将需要的一些其他包。 您始终可以根据需要使用conda install或pip install命令安装软件包。
以下命令将激活创建的 Conda 环境。 我们将能够使用安装在其中的包,而无需与全局或其他环境中安装的包混合。
source activate TensorFlowEnvpip 安装工具是 Conda 环境的标准部分。 我们将使用它来安装 TensorFlow 库。 在此之前,好的第一步是将 pip 更新到最新版本,使用以下命令:
pip install --upgrade pip现在我们准备好安装 TensorFlow,运行:
pip install tensorflowTensorFlow 的下载和构建可能需要几分钟时间。 在撰写本文时,这将安装 TensorFlow 1.1.0。
数据流图
在 TensorFlow 中,计算是使用数据流图来描述的。 图的每个节点代表一个数学运算(如加法、除法或乘法)的实例,每条边都是一个多维数据集(张量),在其上执行操作。
由于 TensorFlow 与计算图一起工作,它们在每个节点代表一个操作的实例化的地方进行管理,其中每个操作都有零个或多个输入和零个或多个输出。
TensorFlow 中的边可以分为两类:普通边传输数据结构(张量),其中一个操作的输出可能成为另一操作的输入,特殊边用于控制两个节点之间的依赖关系以设置一个节点等待另一个节点完成的操作顺序。
简单表达式
在我们继续讨论 TensorFlow 的元素之前,我们将首先进行一次使用 TensorFlow 的会议,以了解 TensorFlow 程序的外观。
让我们从简单的表达式开始,假设出于某种原因,我们想以 TensorFlow 方式计算函数y = 5*x + 13 。
在简单的 Python 代码中,它看起来像:
x = -2.0 y = 5*x + 13 print y在这种情况下,这给了我们 3.0 的结果。
现在我们将上述表达式转换为 TensorFlow 项。
常数
在 TensorFlow 中,常量是使用函数常量创建的,该函数具有签名constant(value, dtype=None, shape=None, name='Const', verify_shape=False) ,其中value是一个实际的常量值,将用于进一步计算, dtype是数据类型参数(例如,float32/64、int8/16 等), shape是可选尺寸, name是张量的可选名称,最后一个参数是一个布尔值,表示验证价值观的形式。
如果您需要在训练模型中具有特定值的常量,则可以使用constant对象,如下例所示:
z = tf.constant(5.2, name="x", dtype=tf.float32)变量
TensorFlow 中的变量是包含张量的内存缓冲区,这些张量必须被显式初始化并在图中使用以维护跨会话的状态。 通过简单地调用构造函数,变量被添加到计算图中。
一旦您开始训练模型,变量就特别有用,它们用于保存和更新参数。 作为构造函数的参数传递的初始值表示可以转换或作为张量返回的张量或对象。 这意味着如果我们想用一些预定义的或随机的值填充一个变量,以便之后在训练过程中使用并在迭代中更新,我们可以通过以下方式定义它:
k = tf.Variable(tf.zeros([1]), name="k")在 TensorFlow 中使用变量的另一种方法是在计算中该变量不可训练,可以通过以下方式定义:
k = tf.Variable(tf.add(a, b), trainable=False)会话
为了实际评估节点,我们必须在会话中运行计算图。
会话封装了 TensorFlow 运行时的控制和状态。 没有参数的会话将使用在当前会话中创建的默认图,否则会话类接受一个图参数,该参数将在该会话中执行。
下面是一个简短的代码片段,展示了如何在 TensorFlow 中使用上面定义的术语来计算简单的线性函数。
import tensorflow as tf x = tf.constant(-2.0, name="x", dtype=tf.float32) a = tf.constant(5.0, name="a", dtype=tf.float32) b = tf.constant(13.0, name="b", dtype=tf.float32) y = tf.Variable(tf.add(tf.multiply(a, x), b)) init = tf.global_variables_initializer() with tf.Session() as session: session.run(init) print session.run(y)使用 TensorFlow:定义计算图
使用数据流图的好处是执行模型与其执行分离(在 CPU、GPU 或某种组合上),一旦实现,TensorFlow 中的软件可以在所有复杂性与代码相关的 CPU 或 GPU 上使用执行被隐藏。
计算图可以在使用 TensorFlow 库的过程中构建,而无需显式实例化 Graph 对象。
TensorFlow 中的 Graph 对象可以通过像c = tf.add(a, b)这样的简单代码行来创建。 这将创建一个操作节点,该节点采用两个张量a和b ,产生它们的总和c作为输出。
计算图是一个使用库的内置进程,无需直接调用图对象。 TensorFlow 中的图形对象包含一组操作和张量作为数据单元,用于在允许相同过程的操作之间使用,并且包含多个图形,其中每个图形将分配给不同的会话。 例如,简单的代码行c = tf.add(a, b)将创建一个操作节点,该节点将两个张量a和b作为输入,并产生它们的总和c作为输出。
TensorFlow 还提供了一种馈送机制,用于将张量修补到图中的任何操作,其中馈送用张量值替换操作的输出。 提要数据在run()函数调用中作为参数传递。
占位符是 TensorFlow 允许开发人员通过绑定在某些表达式中的占位符将数据注入计算图中的方式。 占位符的签名是:
placeholder(dtype, shape=None, name=None)其中 dtype 是张量中元素的类型,可以提供要输入的张量的形状和操作的名称。
如果形状没有通过,这个张量可以被输入任何形状。 一个重要的注意事项是占位符张量必须提供数据,否则,在执行会话时,如果缺少该部分,占位符会生成具有以下结构的错误:
InvalidArgumentError (see above for traceback): You must feed a value for placeholder tensor 'y' with dtype float占位符的优点是它们允许开发人员创建操作和一般的计算图,而无需为此提前提供数据,并且可以在运行时从外部源添加数据。
让我们来看一个简单的问题,即以 TensorFlow 方式将两个整数x和y相乘,其中一个占位符将通过 session run方法与 feed 机制一起使用。
import tensorflow as tf x = tf.placeholder(tf.float32, name="x") y = tf.placeholder(tf.float32, name="y") z = tf.multiply(x, y, name="z") with tf.Session() as session: print session.run(z, feed_dict={x: 2.1, y: 3.0})使用 TensorBoard 可视化计算图
TensorBoard 是一个用于分析数据流图的可视化工具。 这对于更好地理解机器学习模型很有用。
使用 TensorBoard,您可以深入了解有关参数的不同类型的统计数据以及有关计算图的一般部分的详细信息。 深度神经网络具有大量节点并不罕见。 TensorBoard 允许开发人员深入了解每个节点以及如何在 TensorFlow 运行时执行计算。
现在让我们回到本 TensorFlow 教程开头的示例,其中我们定义了格式y = a*x + b的线性函数。
为了记录会话中的事件,以后可以在 TensorBoard 中使用,TensorFlow 提供了FileWriter类。 它可用于创建事件文件以存储摘要,其中构造函数接受六个参数,如下所示:
__init__(logdir, graph=None, max_queue=10, flush_secs=120, graph_def=None, filename_suffix=None)其中 logdir 参数是必需的,其他有默认值。 图参数将从训练程序中创建的会话对象传递。 完整的示例代码如下所示:
import tensorflow as tf x = tf.constant(-2.0, name="x", dtype=tf.float32) a = tf.constant(5.0, name="a", dtype=tf.float32) b = tf.constant(13.0, name="b", dtype=tf.float32) y = tf.Variable(tf.add(tf.multiply(a, x), b)) init = tf.global_variables_initializer() with tf.Session() as session: merged = tf.summary.merge_all() // new writer = tf.summary.FileWriter("logs", session.graph) // new session.run(init) print session.run(y) 我们只添加了两条新线。 我们合并了默认图表中收集的所有摘要,并且FileWriter分别用于将事件转储到文件中,如上所述。
运行程序后,我们在目录日志中有文件,最后一步是运行tensorboard :
tensorboard --logdir logs/ 现在 TensorBoard 已启动并在默认端口 6006 上运行。打开http://localhost:6006并单击 Graphs 菜单项(位于页面顶部)后,您将能够看到图形,就像在下图中:
TensorBoard 标记常量和汇总节点特定符号,如下所述。
TensorFlow 数学
张量是 TensorFlow 中的基本数据结构,它们表示数据流图中的连接边。
张量只是标识一个多维数组或列表。 张量结构可以用三个参数来识别:等级、形状和类型。
- Rank:标识张量的维数。 秩称为张量的阶数或 n 维,例如,秩 1 的张量是向量或秩 2 的张量是矩阵。
- 形状:张量的形状是它的行数和列数。
- 类型:分配给张量元素的数据类型。
要在 TensorFlow 中构建张量,我们可以构建一个 n 维数组。 这可以通过使用 NumPy 库或将 Python n 维数组转换为 TensorFlow 张量来轻松完成。
为了构建一维张量,我们将使用一个 NumPy 数组,我们将通过传递一个内置的 Python 列表来构建它。
import numpy as np tensor_1d = np.array([1.45, -1, 0.2, 102.1])使用这种数组类似于使用内置 Python 列表。 主要区别在于 NumPy 数组还包含一些附加属性,如维度、形状和类型。
> > print tensor1d [ 1.45 -1. 0.2 102.1 ] > > print tensor1d[0] 1.45 > > print tensor1d[2] 0.2 > > print tensor1d.ndim 1 > > print tensor1d.shape (4,) > > print tensor1d.dtype float64NumPy 数组可以通过辅助函数 convert_to_tensor 轻松转换为 TensorFlow 张量,帮助开发人员将 Python 对象转换为张量对象。 此函数接受张量对象、NumPy 数组、Python 列表和 Python 标量。
tensor = tf.convert_to_tensor(tensor_1d, dtype=tf.float64)现在,如果我们将张量绑定到 TensorFlow 会话,我们将能够看到转换的结果。
tensor = tf.convert_to_tensor(tensor_1d, dtype=tf.float64) with tf.Session() as session: print session.run(tensor) print session.run(tensor[0]) print session.run(tensor[1])输出:
[ 1.45 -1. 0.2 102.1 ] 1.45 -1.0我们可以用类似的方式创建一个二维张量或矩阵:
tensor_2d = np.array(np.random.rand(4, 4), dtype='float32') tensor_2d_1 = np.array(np.random.rand(4, 4), dtype='float32') tensor_2d_2 = np.array(np.random.rand(4, 4), dtype='float32') m1 = tf.convert_to_tensor(tensor_2d) m2 = tf.convert_to_tensor(tensor_2d_1) m3 = tf.convert_to_tensor(tensor_2d_2) mat_product = tf.matmul(m1, m2) mat_sum = tf.add(m2, m3) mat_det = tf.matrix_determinant(m3) with tf.Session() as session: print session.run(mat_product) print session.run(mat_sum) print session.run(mat_det)张量运算
在上面的例子中,我们介绍了一些 TensorFlow 对向量和矩阵的操作。 这些操作对张量执行某些计算。 下表显示了这些计算。
| TensorFlow 算子 | 描述 |
|---|---|
| tf.add | x+y |
| tf.减法 | xy |
| tf.multiply | x*y |
| tf.div | x/y |
| tf.mod | x % y |
| tf.abs | |x| |
| tf.negative | -X |
| tf.sign | 符号(x) |
| 方阵 | x*x |
| tf.round | 回合(x) |
| tf.sqrt | 平方(x) |
| tf.pow | x^y |
| tf.exp | e^x |
| tf.log | 日志(x) |
| tf.最大值 | 最大值(x,y) |
| tf.minimum | 最小值(x, y) |
| tf.cos | 余弦(x) |
| tf.sin | 罪(x) |
上表中列出的 TensorFlow 操作适用于张量对象,并且是按元素执行的。 因此,如果您想计算向量 x 的余弦,TensorFlow 操作将对传递的张量中的每个元素进行计算。
tensor_1d = np.array([0, 0, 0]) tensor = tf.convert_to_tensor(tensor_1d, dtype=tf.float64) with tf.Session() as session: print session.run(tf.cos(tensor))输出:
[ 1. 1. 1.]矩阵运算
矩阵运算对于机器学习模型非常重要,例如线性回归,因为它们经常在其中使用。 TensorFlow 支持所有最常见的矩阵运算,例如乘法、转置、求逆、计算行列式、求解线性方程等等。
接下来,我们将解释一些矩阵运算。 当涉及机器学习模型时,它们往往很重要,例如线性回归。 让我们编写一些代码来执行基本的矩阵运算,例如乘法、获得转置、获得行列式、乘法、sol 等等。
下面是调用这些操作的基本示例。
import tensorflow as tf import numpy as np def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) m1 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m2 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m3 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m4 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m5 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m_tranpose = tf.transpose(m1) m_mul = tf.matmul(m1, m2) m_det = tf.matrix_determinant(m3) m_inv = tf.matrix_inverse(m4) m_solve = tf.matrix_solve(m5, [[1], [1], [1], [1]]) with tf.Session() as session: print session.run(m_tranpose) print session.run(m_mul) print session.run(m_inv) print session.run(m_det) print session.run(m_solve)转换数据
减少
TensorFlow 支持不同类型的归约。 归约是一种通过在这些维度上执行某些操作来从张量中删除一个或多个维度的操作。 可以在此处找到当前版本的 TensorFlow 支持的缩减列表。 我们将在下面的示例中介绍其中的一些。

import tensorflow as tf import numpy as np def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) x = convert( np.array( [ (1, 2, 3), (4, 5, 6), (7, 8, 9) ]), tf.int32) bool_tensor = convert([(True, False, True), (False, False, True), (True, False, False)], tf.bool) red_sum_0 = tf.reduce_sum(x) red_sum = tf.reduce_sum(x, axis=1) red_prod_0 = tf.reduce_prod(x) red_prod = tf.reduce_prod(x, axis=1) red_min_0 = tf.reduce_min(x) red_min = tf.reduce_min(x, axis=1) red_max_0 = tf.reduce_max(x) red_max = tf.reduce_max(x, axis=1) red_mean_0 = tf.reduce_mean(x) red_mean = tf.reduce_mean(x, axis=1) red_bool_all_0 = tf.reduce_all(bool_tensor) red_bool_all = tf.reduce_all(bool_tensor, axis=1) red_bool_any_0 = tf.reduce_any(bool_tensor) red_bool_any = tf.reduce_any(bool_tensor, axis=1) with tf.Session() as session: print "Reduce sum without passed axis parameter: ", session.run(red_sum_0) print "Reduce sum with passed axis=1: ", session.run(red_sum) print "Reduce product without passed axis parameter: ", session.run(red_prod_0) print "Reduce product with passed axis=1: ", session.run(red_prod) print "Reduce min without passed axis parameter: ", session.run(red_min_0) print "Reduce min with passed axis=1: ", session.run(red_min) print "Reduce max without passed axis parameter: ", session.run(red_max_0) print "Reduce max with passed axis=1: ", session.run(red_max) print "Reduce mean without passed axis parameter: ", session.run(red_mean_0) print "Reduce mean with passed axis=1: ", session.run(red_mean) print "Reduce bool all without passed axis parameter: ", session.run(red_bool_all_0) print "Reduce bool all with passed axis=1: ", session.run(red_bool_all) print "Reduce bool any without passed axis parameter: ", session.run(red_bool_any_0) print "Reduce bool any with passed axis=1: ", session.run(red_bool_any)输出:
Reduce sum without passed axis parameter: 45 Reduce sum with passed axis=1: [ 6 15 24] Reduce product without passed axis parameter: 362880 Reduce product with passed axis=1: [ 6 120 504] Reduce min without passed axis parameter: 1 Reduce min with passed axis=1: [1 4 7] Reduce max without passed axis parameter: 9 Reduce max with passed axis=1: [3 6 9] Reduce mean without passed axis parameter: 5 Reduce mean with passed axis=1: [2 5 8] Reduce bool all without passed axis parameter: False Reduce bool all with passed axis=1: [False False False] Reduce bool any without passed axis parameter: True Reduce bool any with passed axis=1: [ True True True]约简算子的第一个参数是我们要约简的张量。 第二个参数是我们想要执行缩减的维度的索引。 该参数是可选的,如果未传递,则将沿所有维度执行归约。
我们可以看一下reduce_sum操作。 我们传递一个二维张量,并希望沿维度 1 减少它。
在我们的例子中,结果总和将是:
[1 + 2 + 3 = 6, 4 + 5 + 6 = 15, 7 + 8 + 9 = 24]如果我们传递维度 0,结果将是:
[1 + 4 + 7 = 12, 2 + 5 + 8 = 15, 3 + 6 + 9 = 18]如果我们不通过任何轴,则结果只是以下各项的总和:
1 + 4 + 7 = 12, 2 + 5 + 8 = 15, 3 + 6 + 9 = 45所有归约函数都有类似的接口,并在 TensorFlow 归约文档中列出。
分割
分段是一个过程,其中一个维度是将维度映射到提供的分段索引的过程,结果元素由索引行确定。
分割实际上是对重复索引下的元素进行分组,因此例如,在我们的例子中,我们在张量tens1上应用了分段 id [0, 0, 1, 2, 2] ,这意味着第一个和第二个数组将在分割后进行转换运算(在我们的例子中求和),将得到一个新数组,它看起来像(2, 8, 1, 0) = (2+0, 5+3, 3-2, -5+5) 。 张量tens1中的第三个元素保持不变,因为它没有分组在任何重复的索引中,并且最后两个数组的求和方式与第一组的情况相同。 除了求和,TensorFlow 还支持乘积、均值、最大值和最小值。
import tensorflow as tf import numpy as np def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) seg_ids = tf.constant([0, 0, 1, 2, 2]) tens1 = convert(np.array([(2, 5, 3, -5), (0, 3, -2, 5), (4, 3, 5, 3), (6, 1, 4, 0), (6, 1, 4, 0)]), tf.int32) tens2 = convert(np.array([1, 2, 3, 4, 5]), tf.int32) seg_sum = tf.segment_sum(tens1, seg_ids) seg_sum_1 = tf.segment_sum(tens2, seg_ids) with tf.Session() as session: print "Segmentation sum tens1: ", session.run(seg_sum) print "Segmentation sum tens2: ", session.run(seg_sum_1) Segmentation sum tens1: [[ 2 8 1 0] [ 4 3 5 3] [12 2 8 0]] Segmentation sum tens2: [3 3 9]序列实用程序
序列实用程序包括以下方法:
- argmin 函数,它返回输入张量轴上具有最小值的索引,
- argmax 函数,它返回输入张量轴上具有最大值的索引,
- setdiff,计算两个数字或字符串列表之间的差异,
- where 函数,它将从两个传递的元素 x 或 y 返回元素,这取决于传递的条件,或者
- unique 函数,它将返回一维张量中的唯一元素。
我们在下面展示了几个执行示例:
import numpy as np import tensorflow as tf def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) x = convert(np.array([ [2, 2, 1, 3], [4, 5, 6, -1], [0, 1, 1, -2], [6, 2, 3, 0] ])) y = convert(np.array([1, 2, 5, 3, 7])) z = convert(np.array([1, 0, 4, 6, 2])) arg_min = tf.argmin(x, 1) arg_max = tf.argmax(x, 1) unique = tf.unique(y) diff = tf.setdiff1d(y, z) with tf.Session() as session: print "Argmin = ", session.run(arg_min) print "Argmax = ", session.run(arg_max) print "Unique_values = ", session.run(unique)[0] print "Unique_idx = ", session.run(unique)[1] print "Setdiff_values = ", session.run(diff)[0] print "Setdiff_idx = ", session.run(diff)[1] print session.run(diff)[1]输出:
Argmin = [2 3 3 3] Argmax = [3 2 1 0] Unique_values = [ 1. 2. 5. 3. 7.] Unique_idx = [0 1 2 3 4] Setdiff_values = [ 5. 3. 7.] Setdiff_idx = [2 3 4]使用 TensorFlow 进行机器学习
在本节中,我们将展示一个使用 TensorFlow 的机器学习用例。 第一个示例是使用 kNN 方法对数据进行分类的算法,第二个示例将使用线性回归算法。
神经网络
第一个算法是k-最近邻(kNN)。 它是一种监督学习算法,使用距离度量(例如欧几里得距离)对训练数据进行分类。 它是最简单的算法之一,但对于数据分类仍然非常强大。 该算法的优点:
- 当训练模型足够大时,准确率很高,并且
- 通常对异常值不敏感,我们不需要对数据进行任何假设。
该算法的缺点:
- 计算成本高,并且
- 需要大量内存,其中需要将新的分类数据添加到所有初始训练实例中。
我们将在此代码示例中使用的距离是欧几里得,它定义了两点之间的距离,如下所示:
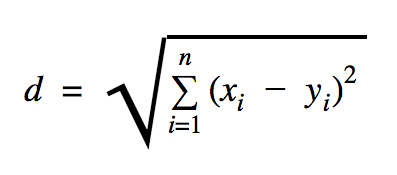
在这个公式中, n是空间的维数, x是训练数据的向量, y是我们要分类的新数据点。
import os import numpy as np import tensorflow as tf ccf_train_data = "train_dataset.csv" ccf_test_data = "test_dataset.csv" dataset_dir = os.path.abspath(os.path.join(os.path.dirname(__file__), '../datasets')) ccf_train_filepath = os.path.join(dataset_dir, ccf_train_data) ccf_test_filepath = os.path.join(dataset_dir, ccf_test_data) def load_data(filepath): from numpy import genfromtxt csv_data = genfromtxt(filepath, delimiter=",", skip_header=1) data = [] labels = [] for d in csv_data: data.append(d[:-1]) labels.append(d[-1]) return np.array(data), np.array(labels) train_dataset, train_labels = load_data(ccf_train_filepath) test_dataset, test_labels = load_data(ccf_test_filepath) train_pl = tf.placeholder("float", [None, 28]) test_pl = tf.placeholder("float", [28]) knn_prediction = tf.reduce_sum(tf.abs(tf.add(train_pl, tf.negative(test_pl))), axis=1) pred = tf.argmin(knn_prediction, 0) with tf.Session() as tf_session: missed = 0 for i in xrange(len(test_dataset)): knn_index = tf_session.run(pred, feed_dict={train_pl: train_dataset, test_pl: test_dataset[i]}) print "Predicted class {} -- True class {}".format(train_labels[knn_index], test_labels[i]) if train_labels[knn_index] != test_labels[i]: missed += 1 tf.summary.FileWriter("../samples/article/logs", tf_session.graph) print "Missed: {} -- Total: {}".format(missed, len(test_dataset))我们在上面示例中使用的数据集是可以在 Kaggle 数据集部分找到的数据集。 我们使用了包含欧洲持卡人信用卡进行的交易的那个。 我们在没有任何清理或过滤的情况下使用数据,并且根据 Kaggle 中对该数据集的描述,它是高度不平衡的。 该数据集包含 31 个变量:时间、V1、...、V28、数量和类别。 在此代码示例中,我们仅使用 V1、...、V28 和 Class。 用 1 标记欺诈性交易,用 0 标记非欺诈性交易。
代码示例主要包含我们在前面部分中描述的内容,但我们介绍了加载数据集的函数。 函数load_data(filepath)将 CSV 文件作为参数,并将返回一个元组,其中包含在 CSV 中定义的数据和标签。
在该函数下方,我们为测试和训练数据定义了占位符。 在预测模型中使用训练数据来解析需要分类的输入数据的标签。 在我们的例子中,kNN 使用欧几里得距离来获得最近的标签。
错误率可以通过简单除以分类器遗漏的样本总数除以该数据集的样本总数(在我们的示例中为 0.2)来计算(即,分类器为 20% 的测试数据提供了错误的数据标签)。
线性回归
线性回归算法寻找两个变量之间的线性关系。 如果我们将因变量标记为 y,将自变量标记为 x,那么我们正在尝试估计函数y = Wx + b的参数。
线性回归是应用科学领域广泛使用的算法。 该算法允许在实现中添加机器学习的两个重要概念:成本函数和用于找到函数最小值的梯度下降法。
使用此方法实现的机器学习算法必须预测y的值作为x的函数,其中线性回归算法将确定值W和b ,它们实际上是未知数,并且在整个训练过程中确定。 选择成本函数,通常使用均方误差,其中梯度下降是用于找到成本函数的局部最小值的优化算法。
梯度下降法只是一个局部函数最小值,但它可以通过在找到局部最小值后随机选择一个新起点并重复该过程多次来用于搜索全局最小值。 如果函数的最小值数量有限并且尝试次数非常多,那么很有可能在某个时候发现全局最小值。 关于这项技术的更多细节,我们将留给我们在介绍部分提到的文章。
import tensorflow as tf import numpy as np test_data_size = 2000 iterations = 10000 learn_rate = 0.005 def generate_test_values(): train_x = [] train_y = [] for _ in xrange(test_data_size): x1 = np.random.rand() x2 = np.random.rand() x3 = np.random.rand() y_f = 2 * x1 + 3 * x2 + 7 * x3 + 4 train_x.append([x1, x2, x3]) train_y.append(y_f) return np.array(train_x), np.transpose([train_y]) x = tf.placeholder(tf.float32, [None, 3], name="x") W = tf.Variable(tf.zeros([3, 1]), name="W") b = tf.Variable(tf.zeros([1]), name="b") y = tf.placeholder(tf.float32, [None, 1]) model = tf.add(tf.matmul(x, W), b) cost = tf.reduce_mean(tf.square(y - model)) train = tf.train.GradientDescentOptimizer(learn_rate).minimize(cost) train_dataset, train_values = generate_test_values() init = tf.global_variables_initializer() with tf.Session() as session: session.run(init) for _ in xrange(iterations): session.run(train, feed_dict={ x: train_dataset, y: train_values }) print "cost = {}".format(session.run(cost, feed_dict={ x: train_dataset, y: train_values })) print "W = {}".format(session.run(W)) print "b = {}".format(session.run(b))输出:
cost = 3.1083032809e-05 W = [[ 1.99049103] [ 2.9887135 ] [ 6.98754263]] b = [ 4.01742554] 在上面的示例中,我们有两个新变量,我们称之为cost和train 。 使用这两个变量,我们定义了一个我们想要在训练模型中使用的优化器和我们想要最小化的函数。
最后, W和b的输出参数应该与generate_test_values函数中定义的相同。 在第 17 行,我们实际上定义了一个函数,用于生成线性数据点以训练w1=2 、 w2=3 、 w3=7和b=4 。 上述示例的线性回归是多元的,其中使用了多个自变量。
结论
正如您在本 TensorFlow 教程中所见,TensorFlow 是一个强大的框架,它使处理数学表达式和多维数组变得轻而易举——这在机器学习中是必不可少的。 它还抽象出执行数据图和缩放的复杂性。
随着时间的推移,TensorFlow 越来越受欢迎,现在被开发人员使用深度学习方法来解决问题,用于图像识别、视频检测、文本处理(如情感分析等)。与任何其他库一样,您可能需要一些时间才能使用TensorFlow 所基于的概念。 而且,一旦你这样做了,在文档和社区支持的帮助下,将问题表示为数据图并使用 TensorFlow 解决它们可以使大规模机器学习变得不那么乏味。
