Noțiuni introductive cu TensorFlow: Un tutorial de învățare automată
Publicat: 2022-03-11TensorFlow este o bibliotecă de software open source creată de Google, care este folosită pentru a implementa sisteme de învățare automată și de deep learning. Aceste două nume conțin o serie de algoritmi puternici care împărtășesc o provocare comună - pentru a permite unui computer să învețe cum să identifice automat modele complexe și/sau să ia cele mai bune decizii posibile.
Dacă sunteți interesat de detalii despre aceste sisteme, puteți afla mai multe din postările de blog Toptal despre învățarea automată și învățarea profundă.
TensorFlow, în centrul său, este o bibliotecă pentru programarea fluxului de date. Utilizează diverse tehnici de optimizare pentru a face calculul expresiilor matematice mai ușor și mai performant.
Unele dintre caracteristicile cheie ale TensorFlow sunt:
- Funcționează eficient cu expresii matematice care implică tablouri multidimensionale
- Sprijin bun pentru rețelele neuronale profunde și conceptele de învățare automată
- Calcul GPU/CPU unde același cod poate fi executat pe ambele arhitecturi
- Scalabilitate ridicată a calculelor pe mașini și seturi uriașe de date
Împreună, aceste caracteristici fac din TensorFlow cadrul perfect pentru inteligența mașinilor la scară de producție.
În acest tutorial TensorFlow, veți afla cum puteți utiliza metode simple, dar puternice de învățare automată în TensorFlow și cum puteți folosi unele dintre bibliotecile sale auxiliare pentru a depana, vizualiza și modifica modelele create cu acesta.
Instalarea TensorFlow
Vom folosi API-ul TensorFlow Python, care funcționează cu Python 2.7 și Python 3.3+. Versiunea GPU (numai Linux) necesită Cuda Toolkit 7.0+ și cuDNN v2+.
Vom folosi sistemul de management al dependenței de pachete Conda pentru a instala TensorFlow. Conda ne permite să separăm mai multe medii pe o mașină. Puteți afla cum să instalați Conda de aici.
După instalarea Conda, putem crea mediul pe care îl vom folosi pentru instalarea și utilizarea TensorFlow. Următoarea comandă va crea mediul nostru cu câteva biblioteci suplimentare precum NumPy, care este foarte utilă odată ce începem să folosim TensorFlow.
Versiunea Python instalată în acest mediu este 2.7 și vom folosi această versiune în acest articol.
conda create --name TensorflowEnv biopython Pentru a ușura lucrurile, instalăm biopython aici în loc de doar NumPy. Aceasta include NumPy și alte câteva pachete de care vom avea nevoie. Puteți instala oricând pachetele așa cum aveți nevoie, folosind conda install sau pip install .
Următoarea comandă va activa mediul Conda creat. Vom putea folosi pachete instalate în el, fără a ne amesteca cu pachete care sunt instalate global sau în alte medii.
source activate TensorFlowEnvInstrumentul de instalare pip este o parte standard a unui mediu Conda. Îl vom folosi pentru a instala biblioteca TensorFlow. Înainte de a face asta, un prim pas bun este actualizarea pip la cea mai recentă versiune, folosind următoarea comandă:
pip install --upgrade pipAcum suntem gata să instalăm TensorFlow, rulând:
pip install tensorflowDescărcarea și construirea TensorFlow poate dura câteva minute. La momentul scrierii, acesta instalează TensorFlow 1.1.0.
Grafice de flux de date
În TensorFlow, calculul este descris folosind grafice de flux de date. Fiecare nod al graficului reprezintă o instanță a unei operații matematice (cum ar fi adunarea, împărțirea sau înmulțirea) și fiecare muchie este un set de date multidimensional (tensor) pe care sunt efectuate operațiile.
Deoarece TensorFlow lucrează cu grafice de calcul, acestea sunt gestionate în care fiecare nod reprezintă instanțiarea unei operații în care fiecare operație are zero sau mai multe intrări și zero sau mai multe ieșiri.
Muchiile din TensorFlow pot fi grupate în două categorii: Muchii normale transferă structură de date (tensori) unde este posibil ca rezultatul unei operații să devină intrarea pentru o altă operație și muchii speciale, care sunt folosite pentru a controla dependența dintre două noduri pentru a seta ordinea de operare în care un nod așteaptă ca altul să se termine.
Expresii simple
Înainte de a trece la discutarea elementelor TensorFlow, vom face mai întâi o sesiune de lucru cu TensorFlow, pentru a avea o idee despre cum arată un program TensorFlow.
Să începem cu expresii simple și să presupunem că, din anumite motive, dorim să evaluăm funcția y = 5*x + 13 în modul TensorFlow.
În codul Python simplu, ar arăta astfel:
x = -2.0 y = 5*x + 13 print ycare ne dă în acest caz un rezultat de 3.0.
Acum vom converti expresia de mai sus în termeni TensorFlow.
constante
În TensorFlow, constantele sunt create folosind constanta funcției, care are constant(value, dtype=None, shape=None, name='Const', verify_shape=False) , unde value este o valoare constantă reală care va fi utilizată în calcul ulterior, dtype este parametrul tipului de date (de exemplu, float32/64, int8/16 etc.), shape este dimensiuni opționale, name este un nume opțional pentru tensor, iar ultimul parametru este un boolean care indică verificarea forma valorilor.
Dacă aveți nevoie de constante cu valori specifice în interiorul modelului dvs. de antrenament, atunci obiectul constant poate fi folosit ca în exemplul următor:
z = tf.constant(5.2, name="x", dtype=tf.float32)Variabile
Variabilele din TensorFlow sunt buffer-uri în memorie care conțin tensori care trebuie să fie inițializați în mod explicit și utilizați în grafic pentru a menține starea în întreaga sesiune. Prin simpla apelare a constructorului, variabila este adăugată în graficul de calcul.
Variabilele sunt deosebit de utile odată ce începeți cu modele de antrenament și sunt folosite pentru a păstra și actualiza parametrii. O valoare inițială transmisă ca argument al unui constructor reprezintă un tensor sau obiect care poate fi convertit sau returnat ca tensor. Aceasta înseamnă că dacă dorim să umplem o variabilă cu niște valori predefinite sau aleatorii care să fie utilizate ulterior în procesul de antrenament și actualizate pe iterații, o putem defini în felul următor:
k = tf.Variable(tf.zeros([1]), name="k")O altă modalitate de a utiliza variabile în TensorFlow este în calcule în care variabila nu este antrenabilă și poate fi definită în felul următor:
k = tf.Variable(tf.add(a, b), trainable=False)Sesiuni
Pentru a evalua efectiv nodurile, trebuie să rulăm un grafic de calcul în cadrul unei sesiuni.
O sesiune încapsulează controlul și starea timpului de execuție TensorFlow. O sesiune fără parametri va folosi graficul implicit creat în sesiunea curentă, în caz contrar clasa de sesiune acceptă un parametru de grafic, care este folosit în acea sesiune pentru a fi executat.
Mai jos este un scurt fragment de cod care arată cum termenii definiți mai sus pot fi utilizați în TensorFlow pentru a calcula o funcție liniară simplă.
import tensorflow as tf x = tf.constant(-2.0, name="x", dtype=tf.float32) a = tf.constant(5.0, name="a", dtype=tf.float32) b = tf.constant(13.0, name="b", dtype=tf.float32) y = tf.Variable(tf.add(tf.multiply(a, x), b)) init = tf.global_variables_initializer() with tf.Session() as session: session.run(init) print session.run(y)Utilizarea TensorFlow: Definirea graficelor computaționale
Lucrul bun despre lucrul cu grafice de flux de date este că modelul de execuție este separat de execuția sa (pe CPU, GPU sau o combinație), unde, odată implementat, software-ul din TensorFlow poate fi folosit pe CPU sau GPU unde toată complexitatea este legată de cod. execuția este ascunsă.
Graficul de calcul poate fi construit în procesul de utilizare a bibliotecii TensorFlow fără a fi nevoie să instanțieze în mod explicit obiectele Graph.
Un obiect Graph în TensorFlow poate fi creat ca rezultat al unei linii simple de cod precum c = tf.add(a, b) . Acest lucru va crea un nod de operație care ia doi tensori a și b care produc suma lor c ca ieșire.
Graficul de calcul este un proces încorporat care utilizează biblioteca fără a fi nevoie să apeleze direct obiectul grafic. Un obiect grafic din TensorFlow, care conține un set de operații și tensori ca unități de date, este utilizat între operații, ceea ce permite același proces și conține mai mult de un grafic în care fiecare grafic va fi alocat unei sesiuni diferite. De exemplu, linia simplă de cod c = tf.add(a, b) va crea un nod de operație care ia doi tensori a și b ca intrare și produce suma lor c ca ieșire.
TensorFlow oferă, de asemenea, un mecanism de alimentare pentru corecția unui tensor la orice operație din grafic, în care fluxul înlocuiește rezultatul unei operații cu valoarea tensorului. Datele de feed sunt transmise ca argument în apelul funcției run() .
Un substituent este modul TensorFlow de a permite dezvoltatorilor să injecteze date în graficul de calcul prin substituenți care sunt legați în interiorul unor expresii. Semnătura substituentului este:
placeholder(dtype, shape=None, name=None)unde dtype este tipul de elemente din tensori și poate furniza atât forma tensoarelor care urmează a fi alimentate, cât și numele operației.
Dacă forma nu este trecută, acest tensor poate fi alimentat cu orice formă. O notă importantă este că tensorul substituentului trebuie alimentat cu date, în caz contrar, la executarea sesiunii și dacă acea parte lipsește, substituentul generează o eroare cu următoarea structură:
InvalidArgumentError (see above for traceback): You must feed a value for placeholder tensor 'y' with dtype floatAvantajul substituenților este că permit dezvoltatorilor să creeze operații și graficul de calcul în general, fără a fi nevoie să furnizeze datele în prealabil pentru asta, iar datele pot fi adăugate în timp de execuție din surse externe.
Să luăm o problemă simplă de înmulțire a două numere întregi x și y în modul TensorFlow, unde un substituent va fi folosit împreună cu un mecanism de alimentare prin metoda de run a sesiunii.
import tensorflow as tf x = tf.placeholder(tf.float32, name="x") y = tf.placeholder(tf.float32, name="y") z = tf.multiply(x, y, name="z") with tf.Session() as session: print session.run(z, feed_dict={x: 2.1, y: 3.0})Vizualizarea graficului de calcul cu TensorBoard
TensorBoard este un instrument de vizualizare pentru analiza graficelor fluxului de date. Acest lucru poate fi util pentru o mai bună înțelegere a modelelor de învățare automată.
Cu TensorBoard, puteți obține o perspectivă asupra diferitelor tipuri de statistici despre parametri și detalii despre părțile graficului de calcul în general. Nu este neobișnuit ca o rețea neuronală profundă să aibă un număr mare de noduri. TensorBoard permite dezvoltatorilor să obțină o perspectivă asupra fiecărui nod și a modului în care calculul este executat în timpul de execuție TensorFlow.
Acum să revenim la exemplul nostru de la începutul acestui tutorial TensorFlow unde am definit o funcție liniară cu formatul y = a*x + b .
Pentru a înregistra evenimente din sesiune care pot fi utilizate ulterior în TensorBoard, TensorFlow oferă clasa FileWriter . Poate fi folosit pentru a crea un fișier de evenimente pentru stocarea rezumatelor în care constructorul acceptă șase parametri și arată astfel:
__init__(logdir, graph=None, max_queue=10, flush_secs=120, graph_def=None, filename_suffix=None)unde este necesar parametrul logdir, iar altele au valori implicite. Parametrul grafic va fi transmis din obiectul sesiune creat în programul de antrenament. Exemplul de cod complet arată astfel:
import tensorflow as tf x = tf.constant(-2.0, name="x", dtype=tf.float32) a = tf.constant(5.0, name="a", dtype=tf.float32) b = tf.constant(13.0, name="b", dtype=tf.float32) y = tf.Variable(tf.add(tf.multiply(a, x), b)) init = tf.global_variables_initializer() with tf.Session() as session: merged = tf.summary.merge_all() // new writer = tf.summary.FileWriter("logs", session.graph) // new session.run(init) print session.run(y) Am adăugat doar două rânduri noi. Îmbinăm toate rezumatele colectate în graficul implicit și FileWriter este folosit pentru a descărca evenimentele în fișier așa cum am descris mai sus, respectiv.
După rularea programului, avem fișierul în jurnalele directorului, iar ultimul pas este să rulăm tensorboard :
tensorboard --logdir logs/ Acum TensorBoard este pornit și rulează pe portul implicit 6006. După ce deschideți http://localhost:6006 și faceți clic pe elementul de meniu Graphs (situat în partea de sus a paginii), veți putea vedea graficul, precum cel in poza de mai jos:
TensorBoard marchează constantele și simbolurile specifice nodurilor rezumative, care sunt descrise mai jos.
Matematică cu TensorFlow
Tensorii sunt structurile de date de bază în TensorFlow și reprezintă marginile de legătură într-un grafic de flux de date.
Un tensor identifică pur și simplu o matrice sau o listă multidimensională. Structura tensorului poate fi identificată cu trei parametri: rang, formă și tip.
- Rang: Identifică numărul de dimensiuni ale tensorului. Un rang este cunoscut ca ordinea sau n-dimensiunile unui tensor, unde de exemplu tensorul rangul 1 este un vector sau tensorul rangul 2 este o matrice.
- Forma: forma unui tensor este numărul de rânduri și coloane pe care le are.
- Tip: tipul de date atribuit elementelor tensoare.
Pentru a construi un tensor în TensorFlow, putem construi o matrice n-dimensională. Acest lucru se poate face cu ușurință prin utilizarea bibliotecii NumPy sau prin conversia unui tablou n-dimensional Python într-un tensor TensorFlow.
Pentru a construi un tensor 1-d, vom folosi o matrice NumPy, pe care o vom construi prin transmiterea unei liste Python încorporate.
import numpy as np tensor_1d = np.array([1.45, -1, 0.2, 102.1])Lucrul cu acest tip de matrice este similar cu lucrul cu o listă Python încorporată. Principala diferență este că matricea NumPy conține și unele proprietăți suplimentare, cum ar fi dimensiunea, forma și tipul.
> > print tensor1d [ 1.45 -1. 0.2 102.1 ] > > print tensor1d[0] 1.45 > > print tensor1d[2] 0.2 > > print tensor1d.ndim 1 > > print tensor1d.shape (4,) > > print tensor1d.dtype float64O matrice NumPy poate fi convertită cu ușurință într-un tensor TensorFlow cu funcția auxiliară convert_to_tensor, care ajută dezvoltatorii să convertească obiectele Python în obiecte tensor. Această funcție acceptă obiecte tensor, matrice NumPy, liste Python și scalari Python.
tensor = tf.convert_to_tensor(tensor_1d, dtype=tf.float64)Acum, dacă ne legăm tensorul la sesiunea TensorFlow, vom putea vedea rezultatele conversiei noastre.
tensor = tf.convert_to_tensor(tensor_1d, dtype=tf.float64) with tf.Session() as session: print session.run(tensor) print session.run(tensor[0]) print session.run(tensor[1])Ieșire:
[ 1.45 -1. 0.2 102.1 ] 1.45 -1.0Putem crea un tensor 2-d, sau o matrice, într-un mod similar:
tensor_2d = np.array(np.random.rand(4, 4), dtype='float32') tensor_2d_1 = np.array(np.random.rand(4, 4), dtype='float32') tensor_2d_2 = np.array(np.random.rand(4, 4), dtype='float32') m1 = tf.convert_to_tensor(tensor_2d) m2 = tf.convert_to_tensor(tensor_2d_1) m3 = tf.convert_to_tensor(tensor_2d_2) mat_product = tf.matmul(m1, m2) mat_sum = tf.add(m2, m3) mat_det = tf.matrix_determinant(m3) with tf.Session() as session: print session.run(mat_product) print session.run(mat_sum) print session.run(mat_det)Operații cu tensori
În exemplul de mai sus, introducem câteva operații TensorFlow pe vectori și matrice. Operațiile efectuează anumite calcule asupra tensoarelor. Ce calcule sunt acestea sunt prezentate în tabelul de mai jos.
| Operatorul TensorFlow | Descriere |
|---|---|
| tf.add | x+y |
| tf.scăderea | X y |
| tf.înmulțire | X y |
| tf.div | X y |
| tf.mod | X y |
| tf.abs | |x| |
| tf.negativ | -X |
| tf.semn | semn(x) |
| tf.pătrat | x*x |
| tf.rotundă | rotund(x) |
| tf.sqrt | sqrt(x) |
| tf.pow | x^y |
| tf.exp | e^x |
| tf.log | log(x) |
| tf.maxim | max(x, y) |
| tf.minimum | min(x, y) |
| tf.cos | cos(x) |
| tf.sin | sin(x) |
Operațiile TensorFlow enumerate în tabelul de mai sus funcționează cu obiecte tensor și sunt efectuate în funcție de elemente. Deci, dacă doriți să calculați cosinusul pentru un vector x, operația TensorFlow va face calcule pentru fiecare element din tensorul trecut.

tensor_1d = np.array([0, 0, 0]) tensor = tf.convert_to_tensor(tensor_1d, dtype=tf.float64) with tf.Session() as session: print session.run(tf.cos(tensor))Ieșire:
[ 1. 1. 1.]Operații cu matrice
Operațiile cu matrice sunt foarte importante pentru modelele de învățare automată, cum ar fi regresia liniară, deoarece sunt adesea folosite în ele. TensorFlow acceptă toate cele mai comune operații matrice, cum ar fi înmulțirea, transpunerea, inversarea, calcularea determinantului, rezolvarea ecuațiilor liniare și multe altele.
În continuare, vom explica câteva dintre operațiile matricei. Ele tind să fie importante atunci când vine vorba de modele de învățare automată, cum ar fi regresia liniară. Să scriem un cod care va face operații matriceale de bază, cum ar fi înmulțirea, obținerea transpunerii, obținerea determinantului, înmulțirea, sol și multe altele.
Mai jos sunt exemple de bază de apelare a acestor operații.
import tensorflow as tf import numpy as np def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) m1 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m2 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m3 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m4 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m5 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m_tranpose = tf.transpose(m1) m_mul = tf.matmul(m1, m2) m_det = tf.matrix_determinant(m3) m_inv = tf.matrix_inverse(m4) m_solve = tf.matrix_solve(m5, [[1], [1], [1], [1]]) with tf.Session() as session: print session.run(m_tranpose) print session.run(m_mul) print session.run(m_inv) print session.run(m_det) print session.run(m_solve)Transformarea datelor
Reducere
TensorFlow acceptă diferite tipuri de reduceri. Reducerea este o operație care elimină una sau mai multe dimensiuni dintr-un tensor prin efectuarea anumitor operații pe acele dimensiuni. O listă a reducerilor acceptate pentru versiunea curentă a TensorFlow poate fi găsită aici. Vom prezenta câteva dintre ele în exemplul de mai jos.
import tensorflow as tf import numpy as np def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) x = convert( np.array( [ (1, 2, 3), (4, 5, 6), (7, 8, 9) ]), tf.int32) bool_tensor = convert([(True, False, True), (False, False, True), (True, False, False)], tf.bool) red_sum_0 = tf.reduce_sum(x) red_sum = tf.reduce_sum(x, axis=1) red_prod_0 = tf.reduce_prod(x) red_prod = tf.reduce_prod(x, axis=1) red_min_0 = tf.reduce_min(x) red_min = tf.reduce_min(x, axis=1) red_max_0 = tf.reduce_max(x) red_max = tf.reduce_max(x, axis=1) red_mean_0 = tf.reduce_mean(x) red_mean = tf.reduce_mean(x, axis=1) red_bool_all_0 = tf.reduce_all(bool_tensor) red_bool_all = tf.reduce_all(bool_tensor, axis=1) red_bool_any_0 = tf.reduce_any(bool_tensor) red_bool_any = tf.reduce_any(bool_tensor, axis=1) with tf.Session() as session: print "Reduce sum without passed axis parameter: ", session.run(red_sum_0) print "Reduce sum with passed axis=1: ", session.run(red_sum) print "Reduce product without passed axis parameter: ", session.run(red_prod_0) print "Reduce product with passed axis=1: ", session.run(red_prod) print "Reduce min without passed axis parameter: ", session.run(red_min_0) print "Reduce min with passed axis=1: ", session.run(red_min) print "Reduce max without passed axis parameter: ", session.run(red_max_0) print "Reduce max with passed axis=1: ", session.run(red_max) print "Reduce mean without passed axis parameter: ", session.run(red_mean_0) print "Reduce mean with passed axis=1: ", session.run(red_mean) print "Reduce bool all without passed axis parameter: ", session.run(red_bool_all_0) print "Reduce bool all with passed axis=1: ", session.run(red_bool_all) print "Reduce bool any without passed axis parameter: ", session.run(red_bool_any_0) print "Reduce bool any with passed axis=1: ", session.run(red_bool_any)Ieșire:
Reduce sum without passed axis parameter: 45 Reduce sum with passed axis=1: [ 6 15 24] Reduce product without passed axis parameter: 362880 Reduce product with passed axis=1: [ 6 120 504] Reduce min without passed axis parameter: 1 Reduce min with passed axis=1: [1 4 7] Reduce max without passed axis parameter: 9 Reduce max with passed axis=1: [3 6 9] Reduce mean without passed axis parameter: 5 Reduce mean with passed axis=1: [2 5 8] Reduce bool all without passed axis parameter: False Reduce bool all with passed axis=1: [False False False] Reduce bool any without passed axis parameter: True Reduce bool any with passed axis=1: [ True True True]Primul parametru al operatorilor de reducere este tensorul pe care dorim să-l reducem. Al doilea parametru sunt indicii de dimensiuni de-a lungul cărora dorim să efectuăm reducerea. Acest parametru este opțional, iar dacă nu este trecut, reducerea va fi efectuată pe toate dimensiunile.
Putem arunca o privire asupra operației reduce_sum. Trecem un tensor 2-d și dorim să-l reducem de-a lungul dimensiunii 1.
În cazul nostru, suma rezultată ar fi:
[1 + 2 + 3 = 6, 4 + 5 + 6 = 15, 7 + 8 + 9 = 24]Dacă am depăși dimensiunea 0, rezultatul ar fi:
[1 + 4 + 7 = 12, 2 + 5 + 8 = 15, 3 + 6 + 9 = 18]Dacă nu trecem nicio axă, rezultatul este doar suma totală a:
1 + 4 + 7 = 12, 2 + 5 + 8 = 15, 3 + 6 + 9 = 45Toate funcțiile de reducere au o interfață similară și sunt enumerate în documentația de reducere TensorFlow.
Segmentarea
Segmentarea este un proces în care una dintre dimensiuni este procesul de mapare a dimensiunilor pe indici de segment furnizați, iar elementele rezultate sunt determinate de un rând de index.
Segmentarea este de fapt gruparea elementelor sub indecși repeți, așa că, de exemplu, în cazul nostru, avem id-uri segmentate [0, 0, 1, 2, 2] aplicate pe tens1 , ceea ce înseamnă că primul și al doilea tablou vor fi transformate în urma segmentării. operație (în cazul nostru însumarea) și va obține o nouă matrice, care arată ca (2, 8, 1, 0) = (2+0, 5+3, 3-2, -5+5) . Al treilea element din tens1 este neatins deoarece nu este grupat în niciun index repetat, iar ultimele două tablouri sunt însumate în același mod ca și în cazul primului grup. Pe lângă sumare, TensorFlow acceptă produs, medie, maxim și min.
import tensorflow as tf import numpy as np def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) seg_ids = tf.constant([0, 0, 1, 2, 2]) tens1 = convert(np.array([(2, 5, 3, -5), (0, 3, -2, 5), (4, 3, 5, 3), (6, 1, 4, 0), (6, 1, 4, 0)]), tf.int32) tens2 = convert(np.array([1, 2, 3, 4, 5]), tf.int32) seg_sum = tf.segment_sum(tens1, seg_ids) seg_sum_1 = tf.segment_sum(tens2, seg_ids) with tf.Session() as session: print "Segmentation sum tens1: ", session.run(seg_sum) print "Segmentation sum tens2: ", session.run(seg_sum_1) Segmentation sum tens1: [[ 2 8 1 0] [ 4 3 5 3] [12 2 8 0]] Segmentation sum tens2: [3 3 9]Utilitare de secvență
Utilitarele de secvență includ metode precum:
- funcția argmin, care returnează indexul cu valoarea minimă pe axele tensorului de intrare,
- funcția argmax, care returnează indicele cu valoarea maximă pe axele tensorului de intrare,
- setdiff, care calculează diferența dintre două liste de numere sau șiruri de caractere,
- unde funcția, care va returna elemente fie din două elemente trecute x sau y, care depinde de condiția trecută, fie
- funcție unică, care va returna elemente unice într-un tensor 1-D.
Demonstrăm mai jos câteva exemple de execuție:
import numpy as np import tensorflow as tf def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) x = convert(np.array([ [2, 2, 1, 3], [4, 5, 6, -1], [0, 1, 1, -2], [6, 2, 3, 0] ])) y = convert(np.array([1, 2, 5, 3, 7])) z = convert(np.array([1, 0, 4, 6, 2])) arg_min = tf.argmin(x, 1) arg_max = tf.argmax(x, 1) unique = tf.unique(y) diff = tf.setdiff1d(y, z) with tf.Session() as session: print "Argmin = ", session.run(arg_min) print "Argmax = ", session.run(arg_max) print "Unique_values = ", session.run(unique)[0] print "Unique_idx = ", session.run(unique)[1] print "Setdiff_values = ", session.run(diff)[0] print "Setdiff_idx = ", session.run(diff)[1] print session.run(diff)[1]Ieșire:
Argmin = [2 3 3 3] Argmax = [3 2 1 0] Unique_values = [ 1. 2. 5. 3. 7.] Unique_idx = [0 1 2 3 4] Setdiff_values = [ 5. 3. 7.] Setdiff_idx = [2 3 4]Învățare automată cu TensorFlow
În această secțiune, vom prezenta un caz de utilizare a învățării automate cu TensorFlow. Primul exemplu va fi un algoritm pentru clasificarea datelor cu abordarea kNN, iar al doilea va folosi algoritmul de regresie liniară.
kNN
Primul algoritm este k-Nearest Neighbors (kNN). Este un algoritm de învățare supravegheat care utilizează metrica distanței, de exemplu distanța euclidiană, pentru a clasifica datele în funcție de antrenament. Este unul dintre cei mai simpli algoritmi, dar încă foarte puternic pentru clasificarea datelor. Avantajele acestui algoritm:
- Oferă o precizie ridicată atunci când modelul de antrenament este suficient de mare și
- De obicei, nu este sensibil la valori aberante și nu trebuie să avem ipoteze despre date.
Dezavantajele acestui algoritm:
- scump din punct de vedere informatic și
- Necesită multă memorie în care trebuie adăugate noi date clasificate la toate instanțele de instruire inițială.
Distanța pe care o vom folosi în acest exemplu de cod este euclidiană, care definește distanța dintre două puncte astfel:
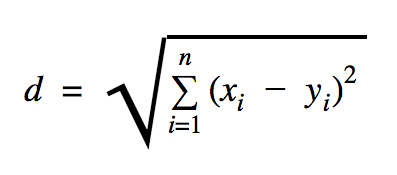
În această formulă, n este numărul de dimensiuni ale spațiului, x este vectorul datelor de antrenament și y este un nou punct de date pe care dorim să-l clasificăm.
import os import numpy as np import tensorflow as tf ccf_train_data = "train_dataset.csv" ccf_test_data = "test_dataset.csv" dataset_dir = os.path.abspath(os.path.join(os.path.dirname(__file__), '../datasets')) ccf_train_filepath = os.path.join(dataset_dir, ccf_train_data) ccf_test_filepath = os.path.join(dataset_dir, ccf_test_data) def load_data(filepath): from numpy import genfromtxt csv_data = genfromtxt(filepath, delimiter=",", skip_header=1) data = [] labels = [] for d in csv_data: data.append(d[:-1]) labels.append(d[-1]) return np.array(data), np.array(labels) train_dataset, train_labels = load_data(ccf_train_filepath) test_dataset, test_labels = load_data(ccf_test_filepath) train_pl = tf.placeholder("float", [None, 28]) test_pl = tf.placeholder("float", [28]) knn_prediction = tf.reduce_sum(tf.abs(tf.add(train_pl, tf.negative(test_pl))), axis=1) pred = tf.argmin(knn_prediction, 0) with tf.Session() as tf_session: missed = 0 for i in xrange(len(test_dataset)): knn_index = tf_session.run(pred, feed_dict={train_pl: train_dataset, test_pl: test_dataset[i]}) print "Predicted class {} -- True class {}".format(train_labels[knn_index], test_labels[i]) if train_labels[knn_index] != test_labels[i]: missed += 1 tf.summary.FileWriter("../samples/article/logs", tf_session.graph) print "Missed: {} -- Total: {}".format(missed, len(test_dataset))Setul de date pe care l-am folosit în exemplul de mai sus este unul care poate fi găsit în secțiunea seturi de date Kaggle. Am folosit-o pe cea care conține tranzacții efectuate cu cardurile de credit ale deținătorilor de carduri europeni. Folosim datele fără nicio curățare sau filtrare și, conform descrierii din Kaggle pentru acest set de date, este foarte dezechilibrat. Setul de date conține 31 de variabile: Ora, V1, …, V28, Sumă și Clasă. În acest exemplu de cod folosim doar V1, …, V28 și Class. Clasa etichetează tranzacțiile care sunt frauduloase cu 1 și pe cele care nu sunt cu 0.
Exemplul de cod conține în mare parte lucrurile pe care le-am descris în secțiunile anterioare, cu excepția cazului în care am introdus funcția de încărcare a unui set de date. Funcția load_data(filepath) va lua un fișier CSV ca argument și va returna un tuplu cu date și etichete definite în CSV.
Chiar sub această funcție, am definit substituenți pentru datele de testare și antrenate. Datele instruite sunt utilizate în modelul de predicție pentru a rezolva etichetele pentru datele de intrare care trebuie clasificate. În cazul nostru, kNN utilizează distanța euclidiană pentru a obține cea mai apropiată etichetă.
Rata de eroare poate fi calculată prin simplă împărțire cu numărul când un clasificator a ratat numărul total de exemple, care în cazul nostru pentru acest set de date este 0,2 (adică, clasificatorul ne oferă eticheta de date greșită pentru 20% din datele de testare).
Regresie liniara
Algoritmul de regresie liniară caută o relație liniară între două variabile. Dacă etichetăm variabila dependentă ca y și variabila independentă ca x, atunci încercăm să estimăm parametrii funcției y = Wx + b .
Regresia liniară este un algoritm utilizat pe scară largă în domeniul științelor aplicate. Acest algoritm permite adăugarea în implementare a două concepte importante de învățare automată: funcția de cost și metoda de coborâre a gradientului pentru găsirea minimului funcției.
Un algoritm de învățare automată care este implementat folosind această metodă trebuie să prezică valorile lui y în funcție de x , unde un algoritm de regresie liniară va determina valorile W și b , care sunt de fapt necunoscute și care sunt determinate de-a lungul procesului de antrenament. Se alege o funcție de cost și, de obicei, eroarea pătratică medie este utilizată în cazul în care coborârea gradientului este algoritmul de optimizare utilizat pentru a găsi un minim local al funcției de cost.
Metoda de coborâre a gradientului este doar un minim local al funcției, dar poate fi folosită în căutarea unui minim global prin alegerea aleatorie a unui nou punct de plecare odată ce a găsit un minim local și repetând acest proces de multe ori. Dacă numărul de minime ale funcției este limitat și există un număr foarte mare de încercări, atunci există șanse mari ca la un moment dat minimul global să fie reperat. Mai multe detalii despre această tehnică le vom lăsa pentru articolul pe care l-am menționat în secțiunea de introducere.
import tensorflow as tf import numpy as np test_data_size = 2000 iterations = 10000 learn_rate = 0.005 def generate_test_values(): train_x = [] train_y = [] for _ in xrange(test_data_size): x1 = np.random.rand() x2 = np.random.rand() x3 = np.random.rand() y_f = 2 * x1 + 3 * x2 + 7 * x3 + 4 train_x.append([x1, x2, x3]) train_y.append(y_f) return np.array(train_x), np.transpose([train_y]) x = tf.placeholder(tf.float32, [None, 3], name="x") W = tf.Variable(tf.zeros([3, 1]), name="W") b = tf.Variable(tf.zeros([1]), name="b") y = tf.placeholder(tf.float32, [None, 1]) model = tf.add(tf.matmul(x, W), b) cost = tf.reduce_mean(tf.square(y - model)) train = tf.train.GradientDescentOptimizer(learn_rate).minimize(cost) train_dataset, train_values = generate_test_values() init = tf.global_variables_initializer() with tf.Session() as session: session.run(init) for _ in xrange(iterations): session.run(train, feed_dict={ x: train_dataset, y: train_values }) print "cost = {}".format(session.run(cost, feed_dict={ x: train_dataset, y: train_values })) print "W = {}".format(session.run(W)) print "b = {}".format(session.run(b))Ieșire:
cost = 3.1083032809e-05 W = [[ 1.99049103] [ 2.9887135 ] [ 6.98754263]] b = [ 4.01742554] În exemplul de mai sus, avem două variabile noi, pe care le-am numit cost și train . Cu aceste două variabile, am definit un optimizator pe care dorim să-l folosim în modelul nostru de antrenament și funcția pe care dorim să o minimizăm.
La sfârșit, parametrii de ieșire ai lui W și b ar trebui să fie identici cu cei definiți în funcția generate_test_values . În linia 17, am definit de fapt o funcție pe care am folosit-o pentru a genera punctele de date liniare pentru a antrena unde w1=2 , w2=3 , w3=7 și b=4 . Regresia liniară din exemplul de mai sus este multivariată, unde sunt utilizate mai multe variabile independente.
Concluzie
După cum puteți vedea din acest tutorial TensorFlow, TensorFlow este un cadru puternic care face ca lucrul cu expresii matematice și matrice multidimensionale să fie o ușoară, ceva esențial necesar în învățarea automată. De asemenea, face abstractie de complexitatea executării graficelor de date și a scalării.
De-a lungul timpului, TensorFlow a crescut în popularitate și este acum folosit de dezvoltatori pentru rezolvarea problemelor folosind metode de deep learning pentru recunoașterea imaginilor, detectarea videoclipurilor, procesarea textului, cum ar fi analiza sentimentelor etc. La fel ca orice altă bibliotecă, este posibil să aveți nevoie de ceva timp pentru a vă obișnui la conceptele pe care se bazează TensorFlow. Și, odată ce ați făcut, cu ajutorul documentației și al asistenței comunitare, reprezentarea problemelor ca grafice de date și rezolvarea lor cu TensorFlow poate face ca învățarea automată la scară să fie un proces mai puțin obositor.
