الشروع في العمل مع TensorFlow: برنامج تعليمي لتعلم الآلة
نشرت: 2022-03-11TensorFlow هي مكتبة برامج مفتوحة المصدر أنشأتها Google وتستخدم لتنفيذ أنظمة التعلم الآلي والتعلم العميق. يحتوي هذان الاسمان على سلسلة من الخوارزميات القوية التي تشترك في تحدي مشترك - للسماح لجهاز الكمبيوتر بتعلم كيفية اكتشاف الأنماط المعقدة تلقائيًا و / أو اتخاذ أفضل القرارات الممكنة.
إذا كنت مهتمًا بالتفاصيل حول هذه الأنظمة ، فيمكنك معرفة المزيد من منشورات مدونة Toptal حول التعلم الآلي والتعلم العميق.
TensorFlow ، في جوهرها ، هي مكتبة لبرمجة تدفق البيانات. يستفيد من تقنيات التحسين المختلفة لجعل حساب التعبيرات الرياضية أسهل وأكثر فاعلية.
بعض الميزات الرئيسية لـ TensorFlow هي:
- يعمل بكفاءة مع التعبيرات الرياضية التي تتضمن مصفوفات متعددة الأبعاد
- دعم جيد للشبكات العصبية العميقة ومفاهيم التعلم الآلي
- حوسبة GPU / CPU حيث يمكن تنفيذ نفس الكود على كلا البنيتين
- قابلية تطوير عالية للحسابات عبر الأجهزة ومجموعات البيانات الضخمة
معًا ، تجعل هذه الميزات TensorFlow الإطار المثالي لذكاء الآلة على نطاق الإنتاج.
في هذا البرنامج التعليمي TensorFlow ، ستتعلم كيف يمكنك استخدام أساليب التعلم الآلي البسيطة والفعالة في TensorFlow وكيف يمكنك استخدام بعض المكتبات المساعدة لتصحيح النماذج التي تم إنشاؤها باستخدامها وتصورها وتعديلها.
تثبيت TensorFlow
سنستخدم TensorFlow Python API ، والذي يعمل مع Python 2.7 و Python 3.3+. إصدار GPU (Linux فقط) يتطلب Cuda Toolkit 7.0+ و cuDNN v2 +.
يجب أن نستخدم نظام إدارة تبعية حزمة Conda لتثبيت TensorFlow. تسمح لنا Conda بفصل بيئات متعددة على الجهاز. يمكنك تعلم كيفية تثبيت Conda من هنا.
بعد تثبيت Conda ، يمكننا إنشاء البيئة التي سنستخدمها لتثبيت TensorFlow واستخدامه. سينشئ الأمر التالي بيئتنا مع بعض المكتبات الإضافية مثل NumPy ، وهو أمر مفيد للغاية بمجرد أن نبدأ في استخدام TensorFlow.
إصدار Python المثبت داخل هذه البيئة هو 2.7 ، وسنستخدم هذا الإصدار في هذه المقالة.
conda create --name TensorflowEnv biopython لتسهيل الأمور ، نقوم بتثبيت biopython هنا بدلاً من NumPy فقط. يتضمن ذلك NumPy وبعض الحزم الأخرى التي سنحتاجها. يمكنك دائمًا تثبيت الحزم حسب حاجتك إليها باستخدام أمر conda install أو pip install .
سيقوم الأمر التالي بتنشيط بيئة Conda التي تم إنشاؤها. سنكون قادرين على استخدام الحزم المثبتة بداخله ، دون الاختلاط مع الحزم المثبتة عالميًا أو في بعض البيئات الأخرى.
source activate TensorFlowEnvتعد أداة تثبيت النقطة جزءًا قياسيًا من بيئة Conda. سنستخدمه لتثبيت مكتبة TensorFlow. قبل القيام بذلك ، تتمثل الخطوة الأولى الجيدة في تحديث النقطة إلى أحدث إصدار باستخدام الأمر التالي:
pip install --upgrade pipنحن الآن جاهزون لتثبيت TensorFlow ، من خلال تشغيل:
pip install tensorflowيمكن أن يستغرق تنزيل TensorFlow وإنشائه عدة دقائق. في وقت كتابة هذا التقرير ، تم تثبيت TensorFlow 1.1.0.
الرسوم البيانية لتدفق البيانات
في TensorFlow ، يتم وصف الحساب باستخدام الرسوم البيانية لتدفق البيانات. تمثل كل عقدة في الرسم البياني مثيلًا لعملية حسابية (مثل الجمع أو القسمة أو الضرب) وكل حافة عبارة عن مجموعة بيانات متعددة الأبعاد (موتر) يتم تنفيذ العمليات عليها.
نظرًا لأن TensorFlow يعمل مع الرسوم البيانية الحسابية ، يتم إدارتها حيث تمثل كل عقدة إنشاء مثيل لعملية حيث تحتوي كل عملية على صفر أو أكثر من المدخلات وصفر أو أكثر من المخرجات.
يمكن تجميع الحواف في TensorFlow في فئتين: نقل الحواف العادية هيكل البيانات (موتر) حيث من الممكن أن يصبح ناتج عملية واحدة مدخلًا لعملية أخرى وحواف خاصة ، والتي تُستخدم للتحكم في التبعية بين عقدتين لتعيين ترتيب العملية حيث تنتظر عقدة واحدة حتى تنتهي عقدة أخرى.
تعابير بسيطة
قبل أن ننتقل لمناقشة عناصر TensorFlow ، سنقوم أولاً بجلسة العمل مع TensorFlow ، للتعرف على شكل برنامج TensorFlow.
لنبدأ بتعبيرات بسيطة ونفترض أننا ، لسبب ما ، نريد تقييم الدالة y = 5*x + 13 بطريقة TensorFlow.
في كود Python البسيط ، سيبدو كما يلي:
x = -2.0 y = 5*x + 13 print yوهو ما يعطينا في هذه الحالة النتيجة 3.0.
سنقوم الآن بتحويل التعبير أعلاه إلى شروط TensorFlow.
الثوابت
في TensorFlow ، يتم إنشاء الثوابت باستخدام ثابت الوظيفة ، الذي يحتوي على constant(value, dtype=None, shape=None, name='Const', verify_shape=False) ، حيث value هي قيمة ثابتة فعلية سيتم استخدامها في مزيد من الحساب ، dtype هو معلمة نوع البيانات (على سبيل المثال ، float32 / 64 ، int8 / 16 ، إلخ) ، shape هو أبعاد اختيارية ، name هو اسم اختياري للموتر ، والمعلمة الأخيرة هي قيمة منطقية تشير إلى التحقق من شكل القيم.
إذا كنت بحاجة إلى ثوابت ذات قيم محددة داخل نموذج التدريب الخاص بك ، فيمكن استخدام الكائن constant كما في المثال التالي:
z = tf.constant(5.2, name="x", dtype=tf.float32)المتغيرات
المتغيرات في TensorFlow هي مخازن مؤقتة في الذاكرة تحتوي على موترات والتي يجب أن يتم تهيئتها بشكل صريح واستخدامها في الرسم البياني للحفاظ على الحالة عبر الجلسة. بمجرد استدعاء المُنشئ ، يُضاف المتغير في الرسم البياني الحسابي.
تكون المتغيرات مفيدة بشكل خاص بمجرد أن تبدأ بنماذج التدريب ، ويتم استخدامها للاحتفاظ بالمعلمات وتحديثها. تمثل القيمة الأولية التي تم تمريرها كوسيطة منشئ موترًا أو كائنًا يمكن تحويله أو إرجاعه كموتّر. هذا يعني أنه إذا أردنا ملء متغير ببعض القيم المحددة مسبقًا أو العشوائية لاستخدامها بعد ذلك في عملية التدريب وتحديثها عبر التكرارات ، فيمكننا تحديدها بالطريقة التالية:
k = tf.Variable(tf.zeros([1]), name="k")هناك طريقة أخرى لاستخدام المتغيرات في TensorFlow وهي في العمليات الحسابية حيث لا يمكن تدريب هذا المتغير ويمكن تعريفه بالطريقة التالية:
k = tf.Variable(tf.add(a, b), trainable=False)الجلسات
من أجل تقييم العقد فعليًا ، يجب علينا تشغيل رسم بياني حسابي داخل الجلسة.
جلسة تلخص التحكم وحالة وقت تشغيل TensorFlow. ستستخدم الجلسة بدون معلمات الرسم البياني الافتراضي الذي تم إنشاؤه في الجلسة الحالية ، وإلا فإن فئة الجلسة تقبل معلمة الرسم البياني ، والتي يتم استخدامها في تلك الجلسة ليتم تنفيذها.
يوجد أدناه مقتطف رمز موجز يوضح كيف يمكن استخدام المصطلحات المحددة أعلاه في TensorFlow لحساب دالة خطية بسيطة.
import tensorflow as tf x = tf.constant(-2.0, name="x", dtype=tf.float32) a = tf.constant(5.0, name="a", dtype=tf.float32) b = tf.constant(13.0, name="b", dtype=tf.float32) y = tf.Variable(tf.add(tf.multiply(a, x), b)) init = tf.global_variables_initializer() with tf.Session() as session: session.run(init) print session.run(y)استخدام TensorFlow: تحديد الرسوم البيانية الحسابية
إن الشيء الجيد في العمل مع الرسوم البيانية لتدفق البيانات هو أن نموذج التنفيذ منفصل عن تنفيذه (على وحدة المعالجة المركزية أو وحدة معالجة الرسومات أو بعض التركيبات) حيث ، بمجرد التنفيذ ، يمكن استخدام البرنامج في TensorFlow على وحدة المعالجة المركزية أو وحدة معالجة الرسومات حيث كل التعقيدات المتعلقة بالكود الإعدام مخفي.
يمكن إنشاء الرسم البياني للحساب في عملية استخدام مكتبة TensorFlow دون الحاجة إلى إنشاء مثيل لكائنات الرسم البياني بشكل صريح.
يمكن إنشاء كائن الرسم البياني في TensorFlow كنتيجة لسطر بسيط من التعليمات البرمجية مثل c = tf.add(a, b) . سيؤدي هذا إلى إنشاء عقدة عملية تأخذ اثنين من الموترات a و b التي تنتج مجموعهما c كناتج.
الرسم البياني للحساب هو عملية مضمنة تستخدم المكتبة دون الحاجة إلى استدعاء كائن الرسم البياني مباشرة. يتم استخدام كائن الرسم البياني في TensorFlow ، والذي يحتوي على مجموعة من العمليات والموترات كوحدات بيانات ، بين العمليات التي تسمح بنفس العملية وتحتوي على أكثر من رسم بياني حيث سيتم تخصيص كل رسم بياني لجلسة مختلفة. على سبيل المثال ، فإن السطر البسيط من الكود c = tf.add(a, b) سينشئ عقدة عملية تأخذ اثنين من الموترات a و b كمدخلات وتنتج مجموع c كناتج.
يوفر TensorFlow أيضًا آلية تغذية لتصحيح موتر لأي عملية في الرسم البياني ، حيث تستبدل التغذية ناتج العملية بقيمة الموتر. يتم تمرير بيانات الخلاصة كوسيطة في استدعاء دالة run() .
العنصر النائب هو طريقة TensorFlow للسماح للمطورين بحقن البيانات في الرسم البياني للحساب من خلال العناصر النائبة المرتبطة ببعض التعبيرات. توقيع العنصر النائب هو:
placeholder(dtype, shape=None, name=None)حيث dtype هو نوع العناصر في الموترات ويمكن أن يوفر كل من شكل الموترات المراد تغذيتها واسم العملية.
إذا لم يتم تمرير الشكل ، يمكن تغذية هذا الموتر بأي شكل. ملاحظة مهمة هي أنه يجب تغذية موتر العنصر النائب بالبيانات ، وإلا ، عند تنفيذ الجلسة وإذا كان هذا الجزء مفقودًا ، فإن العنصر النائب يولد خطأ في الهيكل التالي:
InvalidArgumentError (see above for traceback): You must feed a value for placeholder tensor 'y' with dtype floatميزة العناصر النائبة هي أنها تسمح للمطورين بإنشاء عمليات ، والرسم البياني الحسابي بشكل عام ، دون الحاجة إلى توفير البيانات مسبقًا لذلك ، ويمكن إضافة البيانات في وقت التشغيل من مصادر خارجية.
لنأخذ مشكلة بسيطة تتمثل في ضرب عددين صحيحين x و y بطريقة TensorFlow ، حيث سيتم استخدام عنصر نائب مع آلية تغذية من خلال طريقة run الجلسة.
import tensorflow as tf x = tf.placeholder(tf.float32, name="x") y = tf.placeholder(tf.float32, name="y") z = tf.multiply(x, y, name="z") with tf.Session() as session: print session.run(z, feed_dict={x: 2.1, y: 3.0})تصور الرسم البياني الحسابي باستخدام لوحة TensorBoard
TensorBoard هي أداة تصور لتحليل الرسوم البيانية لتدفق البيانات. يمكن أن يكون هذا مفيدًا لاكتساب فهم أفضل لنماذج التعلم الآلي.
باستخدام TensorBoard ، يمكنك الحصول على نظرة ثاقبة لأنواع مختلفة من الإحصائيات حول المعلمات والتفاصيل حول أجزاء الرسم البياني الحسابي بشكل عام. ليس من غير المعتاد أن تحتوي الشبكة العصبية العميقة على عدد كبير من العقد. يسمح TensorBoard للمطورين بالحصول على نظرة ثاقبة لكل عقدة وكيفية تنفيذ الحساب خلال وقت تشغيل TensorFlow.
الآن دعنا نعود إلى مثالنا من بداية هذا البرنامج التعليمي TensorFlow حيث قمنا بتعريف دالة خطية بالتنسيق y = a*x + b .
من أجل تسجيل الأحداث من الجلسة التي يمكن استخدامها لاحقًا في TensorBoard ، يوفر FileWriter فئة FileWriter. يمكن استخدامه لإنشاء ملف حدث لتخزين الملخصات حيث يقبل المنشئ ستة معلمات ويبدو مثل:
__init__(logdir, graph=None, max_queue=10, flush_secs=120, graph_def=None, filename_suffix=None)حيث تكون المعلمة logdir مطلوبة ، بينما يكون للمعلمات الأخرى قيم افتراضية. سيتم تمرير معلمة الرسم البياني من كائن الجلسة الذي تم إنشاؤه في برنامج التدريب. يبدو رمز المثال الكامل كما يلي:
import tensorflow as tf x = tf.constant(-2.0, name="x", dtype=tf.float32) a = tf.constant(5.0, name="a", dtype=tf.float32) b = tf.constant(13.0, name="b", dtype=tf.float32) y = tf.Variable(tf.add(tf.multiply(a, x), b)) init = tf.global_variables_initializer() with tf.Session() as session: merged = tf.summary.merge_all() // new writer = tf.summary.FileWriter("logs", session.graph) // new session.run(init) print session.run(y) أضفنا سطرين جديدين فقط. نقوم بدمج جميع الملخصات التي تم جمعها في الرسم البياني الافتراضي ، ويتم استخدام FileWriter لتفريغ الأحداث في الملف كما وصفنا أعلاه ، على التوالي.
بعد تشغيل البرنامج ، لدينا الملف في سجلات الدليل ، والخطوة الأخيرة هي تشغيل tensorboard :
tensorboard --logdir logs/ تم الآن تشغيل TensorBoard وتشغيله على المنفذ الافتراضي 6006. بعد فتح http://localhost:6006 والنقر فوق عنصر قائمة الرسوم البيانية (الموجود أعلى الصفحة) ، ستتمكن من رؤية الرسم البياني ، مثل ذلك. في الصورة أدناه:
يقوم TensorBoard بوضع علامة على الثوابت ورموز عقد التلخيص المحددة ، الموضحة أدناه.
الرياضيات مع TensorFlow
الموترات هي هياكل البيانات الأساسية في TensorFlow ، وهي تمثل الحواف المتصلة في رسم بياني لتدفق البيانات.
يحدد الموتر ببساطة مصفوفة أو قائمة متعددة الأبعاد. يمكن تحديد هيكل الموتر بثلاث معاملات: الرتبة والشكل والنوع.
- الرتبة: يحدد عدد أبعاد الموتر. تُعرف الرتبة بالترتيب أو أبعاد n للموتر ، حيث على سبيل المثال موتر الرتبة 1 هو متجه أو موتر الرتبة 2 هو مصفوفة.
- الشكل: شكل الموتر هو عدد الصفوف والأعمدة التي يحتوي عليها.
- النوع: نوع البيانات المخصص لعناصر الموتر.
لبناء موتر في TensorFlow ، يمكننا بناء مصفوفة ذات أبعاد n. يمكن القيام بذلك بسهولة باستخدام مكتبة NumPy ، أو عن طريق تحويل مصفوفة Python n إلى موتر TensorFlow.
لبناء موتر 1-d ، سنستخدم مصفوفة NumPy ، والتي سنقوم ببنائها بتمرير قائمة بايثون مضمنة.
import numpy as np tensor_1d = np.array([1.45, -1, 0.2, 102.1])يشبه العمل مع هذا النوع من المصفوفات العمل مع قائمة Python المضمنة. الاختلاف الرئيسي هو أن مصفوفة NumPy تحتوي أيضًا على بعض الخصائص الإضافية ، مثل البعد والشكل والنوع.
> > print tensor1d [ 1.45 -1. 0.2 102.1 ] > > print tensor1d[0] 1.45 > > print tensor1d[2] 0.2 > > print tensor1d.ndim 1 > > print tensor1d.shape (4,) > > print tensor1d.dtype float64يمكن تحويل مصفوفة NumPy بسهولة إلى موتر TensorFlow باستخدام الوظيفة المساعدة convert_to_tensor ، والتي تساعد المطورين على تحويل كائنات Python إلى كائنات موتر. تقبل هذه الوظيفة كائنات الموتر ومصفوفات NumPy وقوائم Python وعدادات Python.
tensor = tf.convert_to_tensor(tensor_1d, dtype=tf.float64)الآن إذا ربطنا الموتر الخاص بنا بجلسة TensorFlow ، فسنكون قادرين على رؤية نتائج تحويلنا.
tensor = tf.convert_to_tensor(tensor_1d, dtype=tf.float64) with tf.Session() as session: print session.run(tensor) print session.run(tensor[0]) print session.run(tensor[1])انتاج:
[ 1.45 -1. 0.2 102.1 ] 1.45 -1.0يمكننا إنشاء موتر أو مصفوفة ثنائية الأبعاد بطريقة مماثلة:
tensor_2d = np.array(np.random.rand(4, 4), dtype='float32') tensor_2d_1 = np.array(np.random.rand(4, 4), dtype='float32') tensor_2d_2 = np.array(np.random.rand(4, 4), dtype='float32') m1 = tf.convert_to_tensor(tensor_2d) m2 = tf.convert_to_tensor(tensor_2d_1) m3 = tf.convert_to_tensor(tensor_2d_2) mat_product = tf.matmul(m1, m2) mat_sum = tf.add(m2, m3) mat_det = tf.matrix_determinant(m3) with tf.Session() as session: print session.run(mat_product) print session.run(mat_sum) print session.run(mat_det)عمليات الموتر
في المثال أعلاه ، نقدم بعض عمليات TensorFlow على المتجهات والمصفوفات. تقوم العمليات بإجراء حسابات معينة على الموترات. الحسابات التي تظهر في الجدول أدناه.
| مشغل TensorFlow | وصف |
|---|---|
| tf.add | س + ص |
| tf.subtract | س ص |
| تضاعف | س * ص |
| tf.div | س / ص |
| tf.mod | س٪ ص |
| tf.abs | | x | |
| tf سلبي | -x |
| tf.sign | علامة (x) |
| tf.square | س * س |
| tf.round | جولة (x) |
| tf.sqrt | الجذر التربيعي (x) |
| tf.pow | س ^ ص |
| tf.exp | ه ^ س |
| tf.log | تسجيل (x) |
| tf الحد الأقصى | ماكس (س ، ص) |
| tf.minimum | دقيقة (س ، ص) |
| tf.cos | كوس (س) |
| tf.sin | الخطيئة (x) |
تعمل عمليات TensorFlow المدرجة في الجدول أعلاه مع كائنات الموتر ، ويتم تنفيذها من حيث العناصر. لذلك إذا كنت تريد حساب جيب التمام للمتجه x ، فستقوم عملية TensorFlow بحسابات لكل عنصر في الموتر الذي تم تمريره.

tensor_1d = np.array([0, 0, 0]) tensor = tf.convert_to_tensor(tensor_1d, dtype=tf.float64) with tf.Session() as session: print session.run(tf.cos(tensor))انتاج:
[ 1. 1. 1.]عمليات المصفوفة
تعتبر عمليات المصفوفة مهمة جدًا لنماذج التعلم الآلي ، مثل الانحدار الخطي ، حيث يتم استخدامها غالبًا فيها. يدعم TensorFlow جميع عمليات المصفوفة الأكثر شيوعًا ، مثل الضرب والتبديل والانعكاس وحساب المحدد وحل المعادلات الخطية وغير ذلك الكثير.
بعد ذلك ، سنشرح بعض عمليات المصفوفة. تميل إلى أن تكون مهمة عندما يتعلق الأمر بنماذج التعلم الآلي ، كما هو الحال في الانحدار الخطي. دعنا نكتب بعض التعليمات البرمجية التي ستنفذ عمليات المصفوفة الأساسية مثل الضرب ، والحصول على المدور ، والحصول على المحدد ، والضرب ، و sol ، وغير ذلك الكثير.
فيما يلي أمثلة أساسية لاستدعاء هذه العمليات.
import tensorflow as tf import numpy as np def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) m1 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m2 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m3 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m4 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m5 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m_tranpose = tf.transpose(m1) m_mul = tf.matmul(m1, m2) m_det = tf.matrix_determinant(m3) m_inv = tf.matrix_inverse(m4) m_solve = tf.matrix_solve(m5, [[1], [1], [1], [1]]) with tf.Session() as session: print session.run(m_tranpose) print session.run(m_mul) print session.run(m_inv) print session.run(m_det) print session.run(m_solve)تحويل البيانات
اختزال
يدعم TensorFlow أنواعًا مختلفة من التخفيض. التخفيض هو عملية تزيل بُعدًا واحدًا أو أكثر من الموتر عن طريق إجراء عمليات معينة عبر تلك الأبعاد. يمكن العثور هنا على قائمة بالتخفيضات المدعومة للإصدار الحالي من TensorFlow. سنقدم القليل منهم في المثال أدناه.
import tensorflow as tf import numpy as np def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) x = convert( np.array( [ (1, 2, 3), (4, 5, 6), (7, 8, 9) ]), tf.int32) bool_tensor = convert([(True, False, True), (False, False, True), (True, False, False)], tf.bool) red_sum_0 = tf.reduce_sum(x) red_sum = tf.reduce_sum(x, axis=1) red_prod_0 = tf.reduce_prod(x) red_prod = tf.reduce_prod(x, axis=1) red_min_0 = tf.reduce_min(x) red_min = tf.reduce_min(x, axis=1) red_max_0 = tf.reduce_max(x) red_max = tf.reduce_max(x, axis=1) red_mean_0 = tf.reduce_mean(x) red_mean = tf.reduce_mean(x, axis=1) red_bool_all_0 = tf.reduce_all(bool_tensor) red_bool_all = tf.reduce_all(bool_tensor, axis=1) red_bool_any_0 = tf.reduce_any(bool_tensor) red_bool_any = tf.reduce_any(bool_tensor, axis=1) with tf.Session() as session: print "Reduce sum without passed axis parameter: ", session.run(red_sum_0) print "Reduce sum with passed axis=1: ", session.run(red_sum) print "Reduce product without passed axis parameter: ", session.run(red_prod_0) print "Reduce product with passed axis=1: ", session.run(red_prod) print "Reduce min without passed axis parameter: ", session.run(red_min_0) print "Reduce min with passed axis=1: ", session.run(red_min) print "Reduce max without passed axis parameter: ", session.run(red_max_0) print "Reduce max with passed axis=1: ", session.run(red_max) print "Reduce mean without passed axis parameter: ", session.run(red_mean_0) print "Reduce mean with passed axis=1: ", session.run(red_mean) print "Reduce bool all without passed axis parameter: ", session.run(red_bool_all_0) print "Reduce bool all with passed axis=1: ", session.run(red_bool_all) print "Reduce bool any without passed axis parameter: ", session.run(red_bool_any_0) print "Reduce bool any with passed axis=1: ", session.run(red_bool_any)انتاج:
Reduce sum without passed axis parameter: 45 Reduce sum with passed axis=1: [ 6 15 24] Reduce product without passed axis parameter: 362880 Reduce product with passed axis=1: [ 6 120 504] Reduce min without passed axis parameter: 1 Reduce min with passed axis=1: [1 4 7] Reduce max without passed axis parameter: 9 Reduce max with passed axis=1: [3 6 9] Reduce mean without passed axis parameter: 5 Reduce mean with passed axis=1: [2 5 8] Reduce bool all without passed axis parameter: False Reduce bool all with passed axis=1: [False False False] Reduce bool any without passed axis parameter: True Reduce bool any with passed axis=1: [ True True True]المعلمة الأولى لمشغلي الاختزال هي الموتر الذي نريد تقليله. المعلمة الثانية هي فهارس الأبعاد التي نريد إجراء التخفيض على طولها. هذه المعلمة اختيارية ، وإذا لم يتم تمريرها ، فسيتم إجراء التخفيض على طول جميع الأبعاد.
يمكننا إلقاء نظرة على عملية تقليل_الجمع. نمرر موترًا ثنائي الأبعاد ، ونريد تقليله على طول البعد 1.
في حالتنا ، سيكون المجموع الناتج:
[1 + 2 + 3 = 6, 4 + 5 + 6 = 15, 7 + 8 + 9 = 24]إذا تجاوزنا البعد 0 ، فستكون النتيجة:
[1 + 4 + 7 = 12, 2 + 5 + 8 = 15, 3 + 6 + 9 = 18]إذا لم نجتاز أي محور ، فإن النتيجة هي مجرد المجموع الكلي لـ:
1 + 4 + 7 = 12, 2 + 5 + 8 = 15, 3 + 6 + 9 = 45جميع وظائف التخفيض لها واجهة مماثلة وهي مدرجة في وثائق تقليل تدفق TensorFlow.
تجزئة
التجزئة هي عملية يكون فيها أحد الأبعاد هو عملية تعيين الأبعاد على فهارس المقطع المتوفرة ، ويتم تحديد العناصر الناتجة بواسطة صف الفهرس.
التقسيم هو في الواقع تجميع العناصر تحت فهارس متكررة ، لذلك على سبيل المثال ، في حالتنا ، لدينا معرفات مجزأة [0, 0, 1, 2, 2] مطبقة على tens1 الموتر 1 ، مما يعني أنه سيتم تحويل المصفوفتين الأولى والثانية بعد التجزئة العملية (في مجموع حالتنا) وستحصل على مصفوفة جديدة تبدو مثل (2, 8, 1, 0) = (2+0, 5+3, 3-2, -5+5) . العنصر الثالث في tensor tens1 لم يمس لأنه لم يتم تجميعه في أي فهرس مكرر ، ويتم جمع المصفوفتين الأخيرتين بنفس الطريقة كما كان الحال بالنسبة للمجموعة الأولى. بجانب الجمع ، يدعم TensorFlow المنتج ، والمتوسط ، والحد الأقصى ، والدقيق.
import tensorflow as tf import numpy as np def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) seg_ids = tf.constant([0, 0, 1, 2, 2]) tens1 = convert(np.array([(2, 5, 3, -5), (0, 3, -2, 5), (4, 3, 5, 3), (6, 1, 4, 0), (6, 1, 4, 0)]), tf.int32) tens2 = convert(np.array([1, 2, 3, 4, 5]), tf.int32) seg_sum = tf.segment_sum(tens1, seg_ids) seg_sum_1 = tf.segment_sum(tens2, seg_ids) with tf.Session() as session: print "Segmentation sum tens1: ", session.run(seg_sum) print "Segmentation sum tens2: ", session.run(seg_sum_1) Segmentation sum tens1: [[ 2 8 1 0] [ 4 3 5 3] [12 2 8 0]] Segmentation sum tens2: [3 3 9]أدوات التسلسل
تتضمن أدوات التسلسل المساعدة طرقًا مثل:
- دالة argmin ، والتي تُرجع الفهرس بقيمة min عبر محاور موتر الإدخال ،
- دالة argmax ، والتي تُرجع الفهرس بقيمة قصوى عبر محاور موتر الإدخال ،
- setdiff ، التي تحسب الفرق بين قائمتين من الأرقام أو السلاسل ،
- حيث الوظيفة ، والتي ستعيد العناصر إما من عنصرين تم تمريرهما x أو y ، والتي تعتمد على الشرط الذي تم تمريره ، أو
- وظيفة فريدة ، والتي ستعيد عناصر فريدة في موتر 1-D.
نعرض بعض أمثلة التنفيذ أدناه:
import numpy as np import tensorflow as tf def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) x = convert(np.array([ [2, 2, 1, 3], [4, 5, 6, -1], [0, 1, 1, -2], [6, 2, 3, 0] ])) y = convert(np.array([1, 2, 5, 3, 7])) z = convert(np.array([1, 0, 4, 6, 2])) arg_min = tf.argmin(x, 1) arg_max = tf.argmax(x, 1) unique = tf.unique(y) diff = tf.setdiff1d(y, z) with tf.Session() as session: print "Argmin = ", session.run(arg_min) print "Argmax = ", session.run(arg_max) print "Unique_values = ", session.run(unique)[0] print "Unique_idx = ", session.run(unique)[1] print "Setdiff_values = ", session.run(diff)[0] print "Setdiff_idx = ", session.run(diff)[1] print session.run(diff)[1]انتاج:
Argmin = [2 3 3 3] Argmax = [3 2 1 0] Unique_values = [ 1. 2. 5. 3. 7.] Unique_idx = [0 1 2 3 4] Setdiff_values = [ 5. 3. 7.] Setdiff_idx = [2 3 4]التعلم الآلي باستخدام TensorFlow
في هذا القسم ، سوف نقدم حالة استخدام التعلم الآلي مع TensorFlow. سيكون المثال الأول عبارة عن خوارزمية لتصنيف البيانات باستخدام نهج kNN ، وسيستخدم الثاني خوارزمية الانحدار الخطي.
kNN
الخوارزمية الأولى هي k-Nearest Neighbours (kNN). إنها خوارزمية تعلم خاضعة للإشراف تستخدم مقاييس المسافة ، على سبيل المثال المسافة الإقليدية ، لتصنيف البيانات مقابل التدريب. إنها واحدة من أبسط الخوارزميات ، لكنها لا تزال قوية بالفعل لتصنيف البيانات. إيجابيات هذه الخوارزمية:
- يعطي دقة عالية عندما يكون نموذج التدريب كبيرًا بما يكفي ، و
- لا يكون عادةً حساسًا للقيم المتطرفة ، ولا نحتاج إلى أي افتراضات حول البيانات.
سلبيات هذه الخوارزمية:
- مكلفة حسابيا ، و
- يتطلب مساحة كبيرة من الذاكرة حيث يلزم إضافة بيانات مصنفة جديدة إلى جميع حالات التدريب الأولية.
المسافة التي سنستخدمها في نموذج الرمز هذا هي الإقليدية ، والتي تحدد المسافة بين نقطتين مثل هذا:
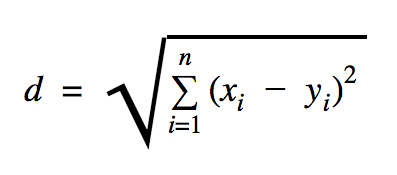
في هذه الصيغة ، n هو عدد أبعاد المساحة ، و x متجه بيانات التدريب ، و y هي نقطة بيانات جديدة نريد تصنيفها.
import os import numpy as np import tensorflow as tf ccf_train_data = "train_dataset.csv" ccf_test_data = "test_dataset.csv" dataset_dir = os.path.abspath(os.path.join(os.path.dirname(__file__), '../datasets')) ccf_train_filepath = os.path.join(dataset_dir, ccf_train_data) ccf_test_filepath = os.path.join(dataset_dir, ccf_test_data) def load_data(filepath): from numpy import genfromtxt csv_data = genfromtxt(filepath, delimiter=",", skip_header=1) data = [] labels = [] for d in csv_data: data.append(d[:-1]) labels.append(d[-1]) return np.array(data), np.array(labels) train_dataset, train_labels = load_data(ccf_train_filepath) test_dataset, test_labels = load_data(ccf_test_filepath) train_pl = tf.placeholder("float", [None, 28]) test_pl = tf.placeholder("float", [28]) knn_prediction = tf.reduce_sum(tf.abs(tf.add(train_pl, tf.negative(test_pl))), axis=1) pred = tf.argmin(knn_prediction, 0) with tf.Session() as tf_session: missed = 0 for i in xrange(len(test_dataset)): knn_index = tf_session.run(pred, feed_dict={train_pl: train_dataset, test_pl: test_dataset[i]}) print "Predicted class {} -- True class {}".format(train_labels[knn_index], test_labels[i]) if train_labels[knn_index] != test_labels[i]: missed += 1 tf.summary.FileWriter("../samples/article/logs", tf_session.graph) print "Missed: {} -- Total: {}".format(missed, len(test_dataset))مجموعة البيانات التي استخدمناها في المثال أعلاه هي مجموعة يمكن العثور عليها في قسم مجموعات بيانات Kaggle. استخدمنا ذلك الذي يحتوي على المعاملات التي تتم بواسطة بطاقات الائتمان لحاملي البطاقات الأوروبية. نحن نستخدم البيانات دون أي تنظيف أو تصفية ووفقًا للوصف الوارد في Kaggle لمجموعة البيانات هذه ، فهي غير متوازنة إلى حد كبير. تحتوي مجموعة البيانات على 31 متغيرًا: الوقت ، V1 ، ... ، V28 ، المبلغ ، والفئة. في نموذج التعليمات البرمجية هذا ، نستخدم فقط V1 و… و V28 و Class. معاملات ملصقات الفئات الاحتيالية مع 1 وتلك التي ليست بها 0.
يحتوي نموذج الشفرة في الغالب على الأشياء التي وصفناها في الأقسام السابقة باستثناء حيث قدمنا وظيفة تحميل مجموعة البيانات. ستأخذ الوظيفة load_data(filepath) ملف CSV كوسيطة وستعيد مجموعة مع البيانات والتسميات المحددة في CSV.
أسفل هذه الوظيفة بقليل ، حددنا عناصر نائبة للاختبار وبيانات مدربة. يتم استخدام البيانات المدربة في نموذج التنبؤ لحل التسميات الخاصة ببيانات الإدخال التي يجب تصنيفها. في حالتنا ، تستخدم kNN المسافة الإقليدية للحصول على أقرب تسمية.
يمكن حساب معدل الخطأ عن طريق القسمة البسيطة مع الرقم عندما غاب المصنف من خلال العدد الإجمالي للأمثلة والذي في حالتنا لمجموعة البيانات هذه هو 0.2 (أي أن المصنف يعطينا تسمية بيانات خاطئة لـ 20٪ من بيانات الاختبار).
الانحدارالخطي
تبحث خوارزمية الانحدار الخطي عن علاقة خطية بين متغيرين. إذا قمنا بتسمية المتغير التابع بـ y ، والمتغير المستقل بـ x ، فإننا نحاول تقدير معلمات الدالة y = Wx + b .
الانحدار الخطي هو خوارزمية مستخدمة على نطاق واسع في مجال العلوم التطبيقية. تسمح هذه الخوارزمية بإضافة مفهومين مهمين للتعلم الآلي في التنفيذ: دالة التكلفة وطريقة نزول التدرج للعثور على الحد الأدنى من الوظيفة.
يجب أن تتنبأ خوارزمية التعلم الآلي التي يتم تنفيذها باستخدام هذه الطريقة بقيم y كدالة لـ x حيث ستحدد خوارزمية الانحدار الخطي القيمتين W و b ، وهما في الواقع غير معروفين ويتم تحديدهما عبر عملية التدريب. يتم اختيار دالة التكلفة ، وعادة ما يتم استخدام متوسط الخطأ التربيعي حيث يكون نزول التدرج هو خوارزمية التحسين المستخدمة للعثور على حد أدنى محلي من دالة التكلفة.
طريقة النسب المتدرجة ليست سوى دالة دنيا محلية ، ولكن يمكن استخدامها في البحث عن حد أدنى عالمي عن طريق اختيار نقطة بداية جديدة بشكل عشوائي بمجرد العثور على حد أدنى محلي وتكرار هذه العملية عدة مرات. إذا كان عدد الحدود الدنيا للوظيفة محدودًا وكان هناك عدد كبير جدًا من المحاولات ، فهناك فرصة جيدة لرصد الحد الأدنى العالمي في مرحلة ما. بعض التفاصيل الإضافية حول هذه التقنية سنتركها للمقال الذي ذكرناه في قسم المقدمة.
import tensorflow as tf import numpy as np test_data_size = 2000 iterations = 10000 learn_rate = 0.005 def generate_test_values(): train_x = [] train_y = [] for _ in xrange(test_data_size): x1 = np.random.rand() x2 = np.random.rand() x3 = np.random.rand() y_f = 2 * x1 + 3 * x2 + 7 * x3 + 4 train_x.append([x1, x2, x3]) train_y.append(y_f) return np.array(train_x), np.transpose([train_y]) x = tf.placeholder(tf.float32, [None, 3], name="x") W = tf.Variable(tf.zeros([3, 1]), name="W") b = tf.Variable(tf.zeros([1]), name="b") y = tf.placeholder(tf.float32, [None, 1]) model = tf.add(tf.matmul(x, W), b) cost = tf.reduce_mean(tf.square(y - model)) train = tf.train.GradientDescentOptimizer(learn_rate).minimize(cost) train_dataset, train_values = generate_test_values() init = tf.global_variables_initializer() with tf.Session() as session: session.run(init) for _ in xrange(iterations): session.run(train, feed_dict={ x: train_dataset, y: train_values }) print "cost = {}".format(session.run(cost, feed_dict={ x: train_dataset, y: train_values })) print "W = {}".format(session.run(W)) print "b = {}".format(session.run(b))انتاج:
cost = 3.1083032809e-05 W = [[ 1.99049103] [ 2.9887135 ] [ 6.98754263]] b = [ 4.01742554] في المثال أعلاه ، لدينا متغيرين جديدين ، أطلقنا عليهما cost train . باستخدام هذين المتغيرين ، حددنا مُحسِّنًا نريد استخدامه في نموذج التدريب الخاص بنا والوظيفة التي نريد تقليلها.
في النهاية ، يجب أن تكون معلمات الإخراج لـ W و b متطابقة مع تلك المحددة في دالة generate_test_values . في السطر 17 ، حددنا بالفعل دالة استخدمناها لإنشاء نقاط البيانات الخطية للتدريب حيث w1=2 ، w2=3 ، w3=7 و b=4 . الانحدار الخطي من المثال أعلاه متعدد المتغيرات حيث يتم استخدام أكثر من متغير مستقل واحد.
خاتمة
كما ترون من هذا البرنامج التعليمي TensorFlow ، فإن TensorFlow هو إطار عمل قوي يجعل العمل مع التعبيرات الرياضية والمصفوفات متعددة الأبعاد أمرًا سهلاً - وهو أمر ضروري بشكل أساسي في التعلم الآلي. كما أنه يزيل تعقيدات تنفيذ الرسوم البيانية للبيانات والقياس.
بمرور الوقت ، نمت شعبية TensorFlow ويتم استخدامها الآن من قبل المطورين لحل المشكلات باستخدام أساليب التعلم العميق للتعرف على الصور واكتشاف الفيديو ومعالجة النصوص مثل تحليل المشاعر وما إلى ذلك ، مثل أي مكتبة أخرى ، قد تحتاج إلى بعض الوقت لتعتاد للمفاهيم التي بنيت عليها TensorFlow. وبمجرد قيامك بذلك ، بمساعدة التوثيق ودعم المجتمع ، فإن تمثيل المشكلات على هيئة رسوم بيانية للبيانات وحلها باستخدام TensorFlow يمكن أن يجعل التعلم الآلي على نطاق واسع عملية أقل مملة.
