Introduzione a TensorFlow: un tutorial sull'apprendimento automatico
Pubblicato: 2022-03-11TensorFlow è una libreria di software open source creata da Google che viene utilizzata per implementare sistemi di machine learning e deep learning. Questi due nomi contengono una serie di potenti algoritmi che condividono una sfida comune: consentire a un computer di imparare come individuare automaticamente schemi complessi e/o prendere le migliori decisioni possibili.
Se sei interessato ai dettagli su questi sistemi, puoi saperne di più dai post del blog Toptal su machine learning e deep learning.
TensorFlow, al suo interno, è una libreria per la programmazione del flusso di dati. Sfrutta varie tecniche di ottimizzazione per rendere il calcolo delle espressioni matematiche più semplice e performante.
Alcune delle caratteristiche principali di TensorFlow sono:
- Funziona in modo efficiente con espressioni matematiche che coinvolgono array multidimensionali
- Buon supporto di reti neurali profonde e concetti di machine learning
- Elaborazione GPU/CPU in cui lo stesso codice può essere eseguito su entrambe le architetture
- Elevata scalabilità del calcolo tra macchine e enormi set di dati
Insieme, queste caratteristiche rendono TensorFlow il framework perfetto per l'intelligenza artificiale su scala di produzione.
In questo tutorial su TensorFlow, imparerai come utilizzare metodi di apprendimento automatico semplici ma potenti in TensorFlow e come puoi utilizzare alcune delle sue librerie ausiliarie per eseguire il debug, visualizzare e modificare i modelli creati con esso.
Installazione di TensorFlow
Utilizzeremo l'API Python di TensorFlow, che funziona con Python 2.7 e Python 3.3+. La versione GPU (solo Linux) richiede Cuda Toolkit 7.0+ e cuDNN v2+.
Utilizzeremo il sistema di gestione delle dipendenze dei pacchetti Conda per installare TensorFlow. Conda ci consente di separare più ambienti su una macchina. Puoi imparare come installare Conda da qui.
Dopo aver installato Conda, possiamo creare l'ambiente che utilizzeremo per l'installazione e l'utilizzo di TensorFlow. Il comando seguente creerà il nostro ambiente con alcune librerie aggiuntive come NumPy, che è molto utile una volta che iniziamo a usare TensorFlow.
La versione di Python installata all'interno di questo ambiente è la 2.7 e useremo questa versione in questo articolo.
conda create --name TensorflowEnv biopython Per semplificare le cose, stiamo installando biopython qui invece di solo NumPy. Ciò include NumPy e alcuni altri pacchetti di cui avremo bisogno. Puoi sempre installare i pacchetti quando ne hai bisogno usando i conda install o pip install .
Il comando seguente attiverà l'ambiente Conda creato. Saremo in grado di utilizzare i pacchetti installati al suo interno, senza mischiare con i pacchetti installati a livello globale o in altri ambienti.
source activate TensorFlowEnvLo strumento di installazione pip è una parte standard di un ambiente Conda. Lo useremo per installare la libreria TensorFlow. Prima di farlo, un buon primo passo è aggiornare pip all'ultima versione, usando il seguente comando:
pip install --upgrade pipOra siamo pronti per installare TensorFlow, eseguendo:
pip install tensorflowIl download e la compilazione di TensorFlow possono richiedere diversi minuti. Al momento della scrittura, questo installa TensorFlow 1.1.0.
Grafici del flusso di dati
In TensorFlow, il calcolo viene descritto utilizzando grafici del flusso di dati. Ogni nodo del grafico rappresenta un'istanza di un'operazione matematica (come addizione, divisione o moltiplicazione) e ogni arco è un set di dati multidimensionale (tensore) su cui vengono eseguite le operazioni.
Poiché TensorFlow lavora con i grafici computazionali, vengono gestiti in cui ogni nodo rappresenta l'istanza di un'operazione in cui ogni operazione ha zero o più input e zero o più output.
Gli spigoli in TensorFlow possono essere raggruppati in due categorie: Gli archi normali trasferiscono la struttura dei dati (tensori) in cui è possibile che l'output di un'operazione diventi l'input per un'altra operazione e gli spigoli speciali, che vengono utilizzati per controllare la dipendenza tra due nodi per impostare il ordine di operazione in cui un nodo attende che un altro finisca.
Espressioni semplici
Prima di passare alla discussione degli elementi di TensorFlow, faremo prima una sessione di lavoro con TensorFlow, per avere un'idea dell'aspetto di un programma TensorFlow.
Iniziamo con espressioni semplici e assumiamo che, per qualche ragione, vogliamo valutare la funzione y = 5*x + 13 in modo TensorFlow.
In un semplice codice Python, sembrerebbe:
x = -2.0 y = 5*x + 13 print yche ci dà in questo caso un risultato di 3.0.
Ora convertiremo l'espressione sopra in termini TensorFlow.
Costanti
In TensorFlow, le costanti vengono create utilizzando la funzione constant, che ha la firma constant(value, dtype=None, shape=None, name='Const', verify_shape=False) , dove value è un valore costante effettivo che verrà utilizzato in ulteriore calcolo, dtype è il parametro del tipo di dati (es. float32/64, int8/16, ecc.), shape è una dimensione opzionale, name è un nome opzionale per il tensore e l'ultimo parametro è un booleano che indica la verifica del forma dei valori.
Se hai bisogno di costanti con valori specifici all'interno del tuo modello di addestramento, l'oggetto constant può essere utilizzato come nell'esempio seguente:
z = tf.constant(5.2, name="x", dtype=tf.float32)Variabili
Le variabili in TensorFlow sono buffer in memoria contenenti tensori che devono essere inizializzati in modo esplicito e utilizzati nel grafico per mantenere lo stato tra le sessioni. Chiamando semplicemente il costruttore la variabile viene aggiunta nel grafico computazionale.
Le variabili sono particolarmente utili quando si inizia con i modelli di addestramento e vengono utilizzate per mantenere e aggiornare i parametri. Un valore iniziale passato come argomento di un costruttore rappresenta un tensore o un oggetto che può essere convertito o restituito come tensore. Ciò significa che se vogliamo riempire una variabile con alcuni valori predefiniti o casuali da utilizzare successivamente nel processo di addestramento e aggiornati su iterazioni, possiamo definirla nel modo seguente:
k = tf.Variable(tf.zeros([1]), name="k")Un altro modo per utilizzare le variabili in TensorFlow è nei calcoli in cui tale variabile non è addestrabile e può essere definita nel modo seguente:
k = tf.Variable(tf.add(a, b), trainable=False)Sessioni
Per valutare effettivamente i nodi, dobbiamo eseguire un grafo computazionale all'interno di una sessione.
Una sessione incapsula il controllo e lo stato del runtime TensorFlow. Una sessione senza parametri utilizzerà il grafico predefinito creato nella sessione corrente, altrimenti la classe di sessione accetta un parametro grafico, che viene utilizzato in quella sessione per essere eseguita.
Di seguito è riportato un breve frammento di codice che mostra come i termini sopra definiti possono essere utilizzati in TensorFlow per calcolare una semplice funzione lineare.
import tensorflow as tf x = tf.constant(-2.0, name="x", dtype=tf.float32) a = tf.constant(5.0, name="a", dtype=tf.float32) b = tf.constant(13.0, name="b", dtype=tf.float32) y = tf.Variable(tf.add(tf.multiply(a, x), b)) init = tf.global_variables_initializer() with tf.Session() as session: session.run(init) print session.run(y)Utilizzo di TensorFlow: definizione di grafici computazionali
L'aspetto positivo dell'utilizzo dei grafici del flusso di dati è che il modello di esecuzione è separato dalla sua esecuzione (su CPU, GPU o una combinazione) dove, una volta implementato, il software in TensorFlow può essere utilizzato sulla CPU o sulla GPU in cui tutta la complessità relativa al codice l'esecuzione è nascosta.
Il grafico di calcolo può essere costruito nel processo di utilizzo della libreria TensorFlow senza dover creare un'istanza esplicita di oggetti Graph.
Un oggetto Graph in TensorFlow può essere creato come risultato di una semplice riga di codice come c = tf.add(a, b) . Questo creerà un nodo operazione che accetta due tensori a che producono la loro somma b come output c
Il grafico di calcolo è un processo integrato che utilizza la libreria senza dover chiamare direttamente l'oggetto grafico. Un oggetto grafico in TensorFlow, che contiene un insieme di operazioni e tensori come unità di dati, viene utilizzato tra le operazioni che consentono lo stesso processo e contiene più di un grafico in cui ciascun grafico verrà assegnato a una sessione diversa. Ad esempio, la semplice riga di codice c = tf.add(a, b) creerà un nodo operativo che accetta due tensori a come input c b output.
TensorFlow fornisce anche un meccanismo di feed per collegare un tensore a qualsiasi operazione nel grafico, in cui il feed sostituisce l'output di un'operazione con il valore del tensore. I dati del feed vengono passati come argomento nella chiamata alla funzione run() .
Un segnaposto è il modo in cui TensorFlow consente agli sviluppatori di inserire dati nel grafico di calcolo tramite segnaposto che sono vincolati all'interno di alcune espressioni. La firma del segnaposto è:
placeholder(dtype, shape=None, name=None)dove dtype è il tipo di elementi nei tensori e può fornire sia la forma dei tensori da alimentare che il nome dell'operazione.
Se la forma non viene superata, questo tensore può essere alimentato con qualsiasi forma. Una nota importante è che il tensore del segnaposto deve essere alimentato con i dati, altrimenti, all'esecuzione della sessione e se quella parte manca, il segnaposto genera un errore con la seguente struttura:
InvalidArgumentError (see above for traceback): You must feed a value for placeholder tensor 'y' with dtype floatIl vantaggio dei segnaposto è che consentono agli sviluppatori di creare operazioni e il grafo computazionale in generale, senza dover fornire i dati in anticipo per questo, e i dati possono essere aggiunti in runtime da fonti esterne.
Prendiamo un semplice problema di moltiplicazione di due interi x in modo y , in cui un segnaposto verrà utilizzato insieme a un meccanismo di feed tramite il metodo di run della sessione.
import tensorflow as tf x = tf.placeholder(tf.float32, name="x") y = tf.placeholder(tf.float32, name="y") z = tf.multiply(x, y, name="z") with tf.Session() as session: print session.run(z, feed_dict={x: 2.1, y: 3.0})Visualizzazione del grafico computazionale con TensorBoard
TensorBoard è uno strumento di visualizzazione per l'analisi dei grafici del flusso di dati. Questo può essere utile per ottenere una migliore comprensione dei modelli di apprendimento automatico.
Con TensorBoard, puoi ottenere informazioni su diversi tipi di statistiche sui parametri e dettagli sulle parti del grafico computazionale in generale. Non è insolito che una rete neurale profonda abbia un gran numero di nodi. TensorBoard consente agli sviluppatori di ottenere informazioni dettagliate su ciascun nodo e su come viene eseguito il calcolo nel runtime di TensorFlow.
Ora torniamo al nostro esempio dall'inizio di questo tutorial di TensorFlow in cui abbiamo definito una funzione lineare con il formato y = a*x + b .
Per registrare gli eventi dalla sessione che in seguito possono essere utilizzati in TensorBoard, TensorFlow fornisce la classe FileWriter . Può essere utilizzato per creare un file di eventi per la memorizzazione di riepiloghi in cui il costruttore accetta sei parametri e ha un aspetto simile a:
__init__(logdir, graph=None, max_queue=10, flush_secs=120, graph_def=None, filename_suffix=None)dove è richiesto il parametro logdir e altri hanno valori predefiniti. Il parametro graph verrà passato dall'oggetto sessione creato nel programma di addestramento. Il codice di esempio completo è simile a:
import tensorflow as tf x = tf.constant(-2.0, name="x", dtype=tf.float32) a = tf.constant(5.0, name="a", dtype=tf.float32) b = tf.constant(13.0, name="b", dtype=tf.float32) y = tf.Variable(tf.add(tf.multiply(a, x), b)) init = tf.global_variables_initializer() with tf.Session() as session: merged = tf.summary.merge_all() // new writer = tf.summary.FileWriter("logs", session.graph) // new session.run(init) print session.run(y) Abbiamo aggiunto solo due nuove righe. Uniamo tutti i riepiloghi raccolti nel grafico predefinito e FileWriter viene utilizzato per eseguire il dump degli eventi nel file come descritto sopra, rispettivamente.
Dopo aver eseguito il programma, abbiamo il file nei registri della directory e l'ultimo passaggio è eseguire tensorboard :
tensorboard --logdir logs/ Ora TensorBoard è avviato ed è in esecuzione sulla porta predefinita 6006. Dopo aver aperto http://localhost:6006 e aver cliccato sulla voce di menu Grafici (che si trova in alto nella pagina), potrai vedere il grafico, come quello nella foto qui sotto:
TensorBoard contrassegna costanti e simboli specifici dei nodi di riepilogo, descritti di seguito.
Matematica con TensorFlow
I tensori sono le strutture di dati di base in TensorFlow e rappresentano i bordi di connessione in un grafico del flusso di dati.
Un tensore identifica semplicemente un array o un elenco multidimensionale. La struttura tensoriale può essere identificata con tre parametri: rango, forma e tipo.
- Rango: Identifica il numero di dimensioni del tensore. Un rango è noto come l'ordine o n-dimensioni di un tensore, dove ad esempio il tensore di rango 1 è un vettore o il tensore di rango 2 è una matrice.
- Forma: La forma di un tensore è il numero di righe e colonne che ha.
- Tipo: il tipo di dati assegnato agli elementi tensore.
Per costruire un tensore in TensorFlow, possiamo costruire un array n-dimensionale. Questo può essere fatto facilmente usando la libreria NumPy o convertendo un array n-dimensionale Python in un tensore TensorFlow.
Per costruire un tensore 1-d, useremo un array NumPy, che costruiremo passando un elenco Python integrato.
import numpy as np tensor_1d = np.array([1.45, -1, 0.2, 102.1])Lavorare con questo tipo di array è simile a lavorare con un elenco Python integrato. La differenza principale è che l'array NumPy contiene anche alcune proprietà aggiuntive, come dimensione, forma e tipo.
> > print tensor1d [ 1.45 -1. 0.2 102.1 ] > > print tensor1d[0] 1.45 > > print tensor1d[2] 0.2 > > print tensor1d.ndim 1 > > print tensor1d.shape (4,) > > print tensor1d.dtype float64Un array NumPy può essere facilmente convertito in un tensore TensorFlow con la funzione ausiliaria convert_to_tensor, che aiuta gli sviluppatori a convertire oggetti Python in oggetti tensore. Questa funzione accetta oggetti tensore, array NumPy, elenchi Python e scalari Python.
tensor = tf.convert_to_tensor(tensor_1d, dtype=tf.float64)Ora, se leghiamo il nostro tensore alla sessione TensorFlow, saremo in grado di vedere i risultati della nostra conversione.
tensor = tf.convert_to_tensor(tensor_1d, dtype=tf.float64) with tf.Session() as session: print session.run(tensor) print session.run(tensor[0]) print session.run(tensor[1])Produzione:
[ 1.45 -1. 0.2 102.1 ] 1.45 -1.0Possiamo creare un tensore 2-d, o matrice, in modo simile:
tensor_2d = np.array(np.random.rand(4, 4), dtype='float32') tensor_2d_1 = np.array(np.random.rand(4, 4), dtype='float32') tensor_2d_2 = np.array(np.random.rand(4, 4), dtype='float32') m1 = tf.convert_to_tensor(tensor_2d) m2 = tf.convert_to_tensor(tensor_2d_1) m3 = tf.convert_to_tensor(tensor_2d_2) mat_product = tf.matmul(m1, m2) mat_sum = tf.add(m2, m3) mat_det = tf.matrix_determinant(m3) with tf.Session() as session: print session.run(mat_product) print session.run(mat_sum) print session.run(mat_det)Operazioni Tensoriale
Nell'esempio sopra, introduciamo alcune operazioni TensorFlow sui vettori e sulle matrici. Le operazioni eseguono determinati calcoli sui tensori. Quali calcoli sono quelli sono mostrati nella tabella seguente.
| Operatore TensorFlow | Descrizione |
|---|---|
| tf.aggiungi | x+y |
| tf.sottrai | xy |
| tf.moltiplicare | x*y |
| tf.div | x/a |
| tf.mod | x % a |
| tf.abs | |x| |
| tf.negativo | -X |
| tf.segno | segno(x) |
| tf.square | x*x |
| tf.round | tondo(x) |
| tf.sqrt | sqrt(x) |
| tf.pow | x^y |
| tf.exp | e^es |
| tf.log | registro(x) |
| tf.massimo | max(x, y) |
| tf.minimo | min(x, y) |
| tf.cos | cos(x) |
| tf.peccato | peccato(x) |
Le operazioni TensorFlow elencate nella tabella precedente funzionano con oggetti tensore e vengono eseguite in base agli elementi. Quindi, se vuoi calcolare il coseno per un vettore x, l'operazione TensorFlow eseguirà i calcoli per ogni elemento nel tensore passato.

tensor_1d = np.array([0, 0, 0]) tensor = tf.convert_to_tensor(tensor_1d, dtype=tf.float64) with tf.Session() as session: print session.run(tf.cos(tensor))Produzione:
[ 1. 1. 1.]Operazioni Matrice
Le operazioni sulle matrici sono molto importanti per i modelli di apprendimento automatico, come la regressione lineare, poiché sono spesso utilizzate in essi. TensorFlow supporta tutte le operazioni di matrice più comuni, come moltiplicazione, trasposizione, inversione, calcolo del determinante, risoluzione di equazioni lineari e molte altre.
Successivamente, spiegheremo alcune delle operazioni sulle matrici. Tendono ad essere importanti quando si tratta di modelli di apprendimento automatico, come nella regressione lineare. Scriviamo del codice che eseguirà operazioni di base sulle matrici come la moltiplicazione, ottenere la trasposizione, ottenere il determinante, la moltiplicazione, il sol e molti altri.
Di seguito sono riportati esempi di base per chiamare queste operazioni.
import tensorflow as tf import numpy as np def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) m1 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m2 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m3 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m4 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m5 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m_tranpose = tf.transpose(m1) m_mul = tf.matmul(m1, m2) m_det = tf.matrix_determinant(m3) m_inv = tf.matrix_inverse(m4) m_solve = tf.matrix_solve(m5, [[1], [1], [1], [1]]) with tf.Session() as session: print session.run(m_tranpose) print session.run(m_mul) print session.run(m_inv) print session.run(m_det) print session.run(m_solve)Trasformare i dati
Riduzione
TensorFlow supporta diversi tipi di riduzione. La riduzione è un'operazione che rimuove una o più dimensioni da un tensore eseguendo determinate operazioni su tali dimensioni. Un elenco delle riduzioni supportate per la versione corrente di TensorFlow è disponibile qui. Ne presenteremo alcuni nell'esempio seguente.
import tensorflow as tf import numpy as np def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) x = convert( np.array( [ (1, 2, 3), (4, 5, 6), (7, 8, 9) ]), tf.int32) bool_tensor = convert([(True, False, True), (False, False, True), (True, False, False)], tf.bool) red_sum_0 = tf.reduce_sum(x) red_sum = tf.reduce_sum(x, axis=1) red_prod_0 = tf.reduce_prod(x) red_prod = tf.reduce_prod(x, axis=1) red_min_0 = tf.reduce_min(x) red_min = tf.reduce_min(x, axis=1) red_max_0 = tf.reduce_max(x) red_max = tf.reduce_max(x, axis=1) red_mean_0 = tf.reduce_mean(x) red_mean = tf.reduce_mean(x, axis=1) red_bool_all_0 = tf.reduce_all(bool_tensor) red_bool_all = tf.reduce_all(bool_tensor, axis=1) red_bool_any_0 = tf.reduce_any(bool_tensor) red_bool_any = tf.reduce_any(bool_tensor, axis=1) with tf.Session() as session: print "Reduce sum without passed axis parameter: ", session.run(red_sum_0) print "Reduce sum with passed axis=1: ", session.run(red_sum) print "Reduce product without passed axis parameter: ", session.run(red_prod_0) print "Reduce product with passed axis=1: ", session.run(red_prod) print "Reduce min without passed axis parameter: ", session.run(red_min_0) print "Reduce min with passed axis=1: ", session.run(red_min) print "Reduce max without passed axis parameter: ", session.run(red_max_0) print "Reduce max with passed axis=1: ", session.run(red_max) print "Reduce mean without passed axis parameter: ", session.run(red_mean_0) print "Reduce mean with passed axis=1: ", session.run(red_mean) print "Reduce bool all without passed axis parameter: ", session.run(red_bool_all_0) print "Reduce bool all with passed axis=1: ", session.run(red_bool_all) print "Reduce bool any without passed axis parameter: ", session.run(red_bool_any_0) print "Reduce bool any with passed axis=1: ", session.run(red_bool_any)Produzione:
Reduce sum without passed axis parameter: 45 Reduce sum with passed axis=1: [ 6 15 24] Reduce product without passed axis parameter: 362880 Reduce product with passed axis=1: [ 6 120 504] Reduce min without passed axis parameter: 1 Reduce min with passed axis=1: [1 4 7] Reduce max without passed axis parameter: 9 Reduce max with passed axis=1: [3 6 9] Reduce mean without passed axis parameter: 5 Reduce mean with passed axis=1: [2 5 8] Reduce bool all without passed axis parameter: False Reduce bool all with passed axis=1: [False False False] Reduce bool any without passed axis parameter: True Reduce bool any with passed axis=1: [ True True True]Il primo parametro degli operatori di riduzione è il tensore che vogliamo ridurre. Il secondo parametro sono gli indici delle dimensioni lungo i quali vogliamo eseguire la riduzione. Tale parametro è facoltativo e, se non viene superato, la riduzione verrà eseguita lungo tutte le dimensioni.
Possiamo dare un'occhiata all'operazione reduce_sum. Passiamo un tensore 2-d e vogliamo ridurlo lungo la dimensione 1.
Nel nostro caso, la somma risultante sarebbe:
[1 + 2 + 3 = 6, 4 + 5 + 6 = 15, 7 + 8 + 9 = 24]Se abbiamo superato la dimensione 0, il risultato sarebbe:
[1 + 4 + 7 = 12, 2 + 5 + 8 = 15, 3 + 6 + 9 = 18]Se non passiamo nessun asse, il risultato è solo la somma complessiva di:
1 + 4 + 7 = 12, 2 + 5 + 8 = 15, 3 + 6 + 9 = 45Tutte le funzioni di riduzione hanno un'interfaccia simile e sono elencate nella documentazione di riduzione di TensorFlow.
Segmentazione
La segmentazione è un processo in cui una delle dimensioni è il processo di mappatura delle dimensioni sugli indici di segmento forniti e gli elementi risultanti sono determinati da una riga di indice.
La segmentazione sta in realtà raggruppando gli elementi sotto indici ripetuti, quindi, ad esempio, nel nostro caso, abbiamo segmentato ids [0, 0, 1, 2, 2] applicato al tensore tens1 , il che significa che il primo e il secondo array verranno trasformati dopo la segmentazione operazione (nel nostro caso la somma) e otterrà un nuovo array, che assomiglia a (2, 8, 1, 0) = (2+0, 5+3, 3-2, -5+5) . Il terzo elemento nel tensore tens1 non viene toccato perché non è raggruppato in alcun indice ripetuto e gli ultimi due array vengono sommati allo stesso modo del primo gruppo. Oltre alla somma, TensorFlow supporta prodotto, media, max e min.
import tensorflow as tf import numpy as np def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) seg_ids = tf.constant([0, 0, 1, 2, 2]) tens1 = convert(np.array([(2, 5, 3, -5), (0, 3, -2, 5), (4, 3, 5, 3), (6, 1, 4, 0), (6, 1, 4, 0)]), tf.int32) tens2 = convert(np.array([1, 2, 3, 4, 5]), tf.int32) seg_sum = tf.segment_sum(tens1, seg_ids) seg_sum_1 = tf.segment_sum(tens2, seg_ids) with tf.Session() as session: print "Segmentation sum tens1: ", session.run(seg_sum) print "Segmentation sum tens2: ", session.run(seg_sum_1) Segmentation sum tens1: [[ 2 8 1 0] [ 4 3 5 3] [12 2 8 0]] Segmentation sum tens2: [3 3 9]Utilità di sequenza
Le utilità di sequenza includono metodi come:
- funzione argmin, che restituisce l'indice con valore minimo sugli assi del tensore di input,
- funzione argmax, che restituisce l'indice con valore massimo sugli assi del tensore di input,
- setdiff, che calcola la differenza tra due elenchi di numeri o stringhe,
- dove funzione, che restituirà elementi da due elementi passati x o y, che dipende dalla condizione passata, o
- funzione unica, che restituirà elementi unici in un tensore 1-D.
Di seguito mostriamo alcuni esempi di esecuzione:
import numpy as np import tensorflow as tf def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) x = convert(np.array([ [2, 2, 1, 3], [4, 5, 6, -1], [0, 1, 1, -2], [6, 2, 3, 0] ])) y = convert(np.array([1, 2, 5, 3, 7])) z = convert(np.array([1, 0, 4, 6, 2])) arg_min = tf.argmin(x, 1) arg_max = tf.argmax(x, 1) unique = tf.unique(y) diff = tf.setdiff1d(y, z) with tf.Session() as session: print "Argmin = ", session.run(arg_min) print "Argmax = ", session.run(arg_max) print "Unique_values = ", session.run(unique)[0] print "Unique_idx = ", session.run(unique)[1] print "Setdiff_values = ", session.run(diff)[0] print "Setdiff_idx = ", session.run(diff)[1] print session.run(diff)[1]Produzione:
Argmin = [2 3 3 3] Argmax = [3 2 1 0] Unique_values = [ 1. 2. 5. 3. 7.] Unique_idx = [0 1 2 3 4] Setdiff_values = [ 5. 3. 7.] Setdiff_idx = [2 3 4]Apprendimento automatico con TensorFlow
In questa sezione presenteremo un caso d'uso di machine learning con TensorFlow. Il primo esempio sarà un algoritmo per classificare i dati con l'approccio kNN e il secondo utilizzerà l'algoritmo di regressione lineare.
kNN
Il primo algoritmo è k-Nearest Neighbors (kNN). È un algoritmo di apprendimento supervisionato che utilizza le metriche della distanza, ad esempio la distanza euclidea, per classificare i dati rispetto all'allenamento. È uno degli algoritmi più semplici, ma comunque molto potente per classificare i dati. Pro di questo algoritmo:
- Fornisce un'elevata precisione quando il modello di addestramento è sufficientemente grande e
- Di solito non è sensibile ai valori anomali e non è necessario avere alcuna ipotesi sui dati.
Contro di questo algoritmo:
- Computazionalmente costoso, e
- Richiede molta memoria in cui è necessario aggiungere nuovi dati classificati a tutte le istanze di addestramento iniziale.
La distanza che useremo in questo esempio di codice è euclidea, che definisce la distanza tra due punti in questo modo:
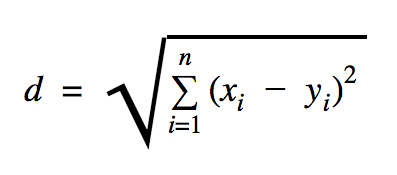
In questa formula, n è il numero di dimensioni dello spazio, x è il vettore dei dati di addestramento e y è un nuovo punto dati che vogliamo classificare.
import os import numpy as np import tensorflow as tf ccf_train_data = "train_dataset.csv" ccf_test_data = "test_dataset.csv" dataset_dir = os.path.abspath(os.path.join(os.path.dirname(__file__), '../datasets')) ccf_train_filepath = os.path.join(dataset_dir, ccf_train_data) ccf_test_filepath = os.path.join(dataset_dir, ccf_test_data) def load_data(filepath): from numpy import genfromtxt csv_data = genfromtxt(filepath, delimiter=",", skip_header=1) data = [] labels = [] for d in csv_data: data.append(d[:-1]) labels.append(d[-1]) return np.array(data), np.array(labels) train_dataset, train_labels = load_data(ccf_train_filepath) test_dataset, test_labels = load_data(ccf_test_filepath) train_pl = tf.placeholder("float", [None, 28]) test_pl = tf.placeholder("float", [28]) knn_prediction = tf.reduce_sum(tf.abs(tf.add(train_pl, tf.negative(test_pl))), axis=1) pred = tf.argmin(knn_prediction, 0) with tf.Session() as tf_session: missed = 0 for i in xrange(len(test_dataset)): knn_index = tf_session.run(pred, feed_dict={train_pl: train_dataset, test_pl: test_dataset[i]}) print "Predicted class {} -- True class {}".format(train_labels[knn_index], test_labels[i]) if train_labels[knn_index] != test_labels[i]: missed += 1 tf.summary.FileWriter("../samples/article/logs", tf_session.graph) print "Missed: {} -- Total: {}".format(missed, len(test_dataset))Il set di dati che abbiamo usato nell'esempio sopra è quello che può essere trovato nella sezione dei set di dati di Kaggle. Abbiamo usato quello che contiene le transazioni effettuate da carte di credito di titolari di carte europei. Stiamo utilizzando i dati senza alcuna pulizia o filtraggio e, come da descrizione in Kaggle per questo set di dati, è altamente sbilanciato. Il set di dati contiene 31 variabili: Time, V1, …, V28, Amount e Class. In questo esempio di codice utilizziamo solo V1, …, V28 e Class. Classe etichetta le transazioni fraudolente con 1 e quelle che non lo sono con 0.
L'esempio di codice contiene principalmente le cose che abbiamo descritto nelle sezioni precedenti con l'eccezione in cui è stata introdotta la funzione per caricare un set di dati. La funzione load_data(filepath) prenderà un file CSV come argomento e restituirà una tupla con dati ed etichette definiti in CSV.
Appena sotto quella funzione, abbiamo definito i segnaposto per i dati di test e addestrati. I dati addestrati vengono utilizzati nel modello di previsione per risolvere le etichette per i dati di input che devono essere classificati. Nel nostro caso, kNN usa la distanza euclidea per ottenere l'etichetta più vicina.
Il tasso di errore può essere calcolato mediante semplice divisione con il numero quando un classificatore ha mancato il numero totale di esempi che nel nostro caso per questo set di dati è 0,2 (cioè, il classificatore ci fornisce l'etichetta dati sbagliata per il 20% dei dati di test).
Regressione lineare
L'algoritmo di regressione lineare cerca una relazione lineare tra due variabili. Se etichettiamo la variabile dipendente come y e la variabile indipendente come x, allora stiamo cercando di stimare i parametri della funzione y = Wx + b .
La regressione lineare è un algoritmo ampiamente utilizzato nel campo delle scienze applicate. Questo algoritmo consente di aggiungere nell'implementazione due importanti concetti di machine learning: la funzione di costo e il metodo di discesa del gradiente per trovare il minimo della funzione.
Un algoritmo di apprendimento automatico implementato utilizzando questo metodo deve prevedere i valori di y in funzione di x dove un algoritmo di regressione lineare determinerà i valori W e b , che sono in realtà sconosciuti e che sono determinati durante il processo di addestramento. Viene scelta una funzione di costo e di solito viene utilizzato l'errore quadratico medio in cui la discesa del gradiente è l'algoritmo di ottimizzazione utilizzato per trovare un minimo locale della funzione di costo.
Il metodo di discesa del gradiente è solo un minimo di una funzione locale, ma può essere utilizzato nella ricerca di un minimo globale scegliendo casualmente un nuovo punto iniziale una volta trovato un minimo locale e ripetendo questo processo molte volte. Se il numero di minimi della funzione è limitato e il numero di tentativi è molto elevato, allora ci sono buone probabilità che a un certo punto venga individuato il minimo globale. Qualche dettaglio in più su questa tecnica lasceremo all'articolo di cui abbiamo parlato nella sezione introduttiva.
import tensorflow as tf import numpy as np test_data_size = 2000 iterations = 10000 learn_rate = 0.005 def generate_test_values(): train_x = [] train_y = [] for _ in xrange(test_data_size): x1 = np.random.rand() x2 = np.random.rand() x3 = np.random.rand() y_f = 2 * x1 + 3 * x2 + 7 * x3 + 4 train_x.append([x1, x2, x3]) train_y.append(y_f) return np.array(train_x), np.transpose([train_y]) x = tf.placeholder(tf.float32, [None, 3], name="x") W = tf.Variable(tf.zeros([3, 1]), name="W") b = tf.Variable(tf.zeros([1]), name="b") y = tf.placeholder(tf.float32, [None, 1]) model = tf.add(tf.matmul(x, W), b) cost = tf.reduce_mean(tf.square(y - model)) train = tf.train.GradientDescentOptimizer(learn_rate).minimize(cost) train_dataset, train_values = generate_test_values() init = tf.global_variables_initializer() with tf.Session() as session: session.run(init) for _ in xrange(iterations): session.run(train, feed_dict={ x: train_dataset, y: train_values }) print "cost = {}".format(session.run(cost, feed_dict={ x: train_dataset, y: train_values })) print "W = {}".format(session.run(W)) print "b = {}".format(session.run(b))Produzione:
cost = 3.1083032809e-05 W = [[ 1.99049103] [ 2.9887135 ] [ 6.98754263]] b = [ 4.01742554] Nell'esempio sopra, abbiamo due nuove variabili, che abbiamo chiamato cost e train . Con queste due variabili, abbiamo definito un ottimizzatore che vogliamo utilizzare nel nostro modello di allenamento e la funzione che vogliamo ridurre al minimo.
Alla fine, i parametri di output di W e b dovrebbero essere identici a quelli definiti nella funzione generate_test_values . Nella riga 17, abbiamo effettivamente definito una funzione che abbiamo usato per generare i punti dati lineari da addestrare dove w1=2 , w2=3 , w3=7 e b=4 . La regressione lineare dell'esempio precedente è multivariata in cui vengono utilizzate più variabili indipendenti.
Conclusione
Come puoi vedere da questo tutorial su TensorFlow, TensorFlow è un potente framework che rende il lavoro con espressioni matematiche e array multidimensionali un gioco da ragazzi, qualcosa di fondamentalmente necessario nell'apprendimento automatico. Astrae anche le complessità dell'esecuzione dei grafici dei dati e del ridimensionamento.
Nel tempo, TensorFlow è diventato popolare e ora viene utilizzato dagli sviluppatori per risolvere problemi utilizzando metodi di deep learning per il riconoscimento di immagini, il rilevamento di video, l'elaborazione di testi come l'analisi dei sentimenti, ecc. Come qualsiasi altra libreria, potrebbe essere necessario del tempo per abituarsi ai concetti su cui si basa TensorFlow. E, una volta fatto, con l'aiuto della documentazione e del supporto della community, rappresentare i problemi come grafici di dati e risolverli con TensorFlow può rendere l'apprendimento automatico su larga scala un processo meno noioso.
