Primeiros passos com o TensorFlow: um tutorial de aprendizado de máquina
Publicados: 2022-03-11O TensorFlow é uma biblioteca de software de código aberto criada pelo Google que é usada para implementar sistemas de aprendizado de máquina e aprendizado profundo. Esses dois nomes contêm uma série de algoritmos poderosos que compartilham um desafio comum – permitir que um computador aprenda a identificar automaticamente padrões complexos e/ou a tomar as melhores decisões possíveis.
Se você estiver interessado em detalhes sobre esses sistemas, saiba mais nas postagens do blog da Toptal sobre aprendizado de máquina e aprendizado profundo.
O TensorFlow, em sua essência, é uma biblioteca para programação de fluxo de dados. Ele aproveita várias técnicas de otimização para tornar o cálculo de expressões matemáticas mais fácil e com melhor desempenho.
Alguns dos principais recursos do TensorFlow são:
- Trabalha eficientemente com expressões matemáticas envolvendo arrays multidimensionais
- Bom suporte de redes neurais profundas e conceitos de aprendizado de máquina
- Computação GPU/CPU onde o mesmo código pode ser executado em ambas as arquiteturas
- Alta escalabilidade de computação entre máquinas e grandes conjuntos de dados
Juntos, esses recursos tornam o TensorFlow a estrutura perfeita para inteligência de máquina em escala de produção.
Neste tutorial do TensorFlow, você aprenderá como usar métodos de aprendizado de máquina simples e poderosos no TensorFlow e como usar algumas de suas bibliotecas auxiliares para depurar, visualizar e ajustar os modelos criados com ele.
Instalando o TensorFlow
Usaremos a API TensorFlow Python, que funciona com Python 2.7 e Python 3.3+. A versão GPU (somente Linux) requer o Cuda Toolkit 7.0+ e o cuDNN v2+.
Usaremos o sistema de gerenciamento de dependências do pacote Conda para instalar o TensorFlow. Conda nos permite separar vários ambientes em uma máquina. Você pode aprender como instalar o Conda aqui.
Após instalar o Conda, podemos criar o ambiente que usaremos para instalação e uso do TensorFlow. O comando a seguir criará nosso ambiente com algumas bibliotecas adicionais como NumPy, que é muito útil quando começamos a usar o TensorFlow.
A versão do Python instalada nesse ambiente é 2.7, e usaremos essa versão neste artigo.
conda create --name TensorflowEnv biopython Para facilitar as coisas, estamos instalando o biopython aqui em vez de apenas o NumPy. Isso inclui o NumPy e alguns outros pacotes que precisaremos. Você sempre pode instalar os pacotes conforme necessário usando os conda install ou pip install .
O comando a seguir ativará o ambiente Conda criado. Poderemos usar pacotes instalados nele, sem misturar com pacotes instalados globalmente ou em alguns outros ambientes.
source activate TensorFlowEnvA ferramenta de instalação pip é uma parte padrão de um ambiente Conda. Vamos usá-lo para instalar a biblioteca TensorFlow. Antes de fazer isso, um bom primeiro passo é atualizar o pip para a versão mais recente, usando o seguinte comando:
pip install --upgrade pipAgora estamos prontos para instalar o TensorFlow, executando:
pip install tensorflowO download e a compilação do TensorFlow podem levar vários minutos. No momento da escrita, isso instala o TensorFlow 1.1.0.
Gráficos de fluxo de dados
No TensorFlow, a computação é descrita usando gráficos de fluxo de dados. Cada nó do gráfico representa uma instância de uma operação matemática (como adição, divisão ou multiplicação) e cada aresta é um conjunto de dados multidimensional (tensor) no qual as operações são executadas.
Como o TensorFlow trabalha com gráficos computacionais, eles são gerenciados onde cada nó representa a instanciação de uma operação onde cada operação tem zero ou mais entradas e zero ou mais saídas.
As arestas no TensorFlow podem ser agrupadas em duas categorias: arestas normais transferem a estrutura de dados (tensores) onde é possível que a saída de uma operação se torne a entrada para outra operação e arestas especiais, que são usadas para controlar a dependência entre dois nós para definir a ordem de operação em que um nó espera que outro termine.
Expressões Simples
Antes de discutirmos os elementos do TensorFlow, primeiro faremos uma sessão de trabalho com o TensorFlow, para ter uma ideia de como é um programa do TensorFlow.
Vamos começar com expressões simples e assumir que, por algum motivo, queremos avaliar a função y = 5*x + 13 no modo TensorFlow.
Em código Python simples, ficaria assim:
x = -2.0 y = 5*x + 13 print yo que nos dá neste caso um resultado de 3,0.
Agora vamos converter a expressão acima em termos do TensorFlow.
Constantes
No TensorFlow, as constantes são criadas usando a função constant, que tem a assinatura constant(value, dtype=None, shape=None, name='Const', verify_shape=False) , onde value é um valor constante real que será usado em computação adicional, dtype é o parâmetro de tipo de dados (por exemplo, float32/64, int8/16, etc.), shape é dimensões opcionais, name é um nome opcional para o tensor e o último parâmetro é um booleano que indica a verificação do forma de valores.
Se você precisar de constantes com valores específicos dentro do seu modelo de treinamento, o objeto constant pode ser usado como no exemplo a seguir:
z = tf.constant(5.2, name="x", dtype=tf.float32)Variáveis
As variáveis no TensorFlow são buffers na memória contendo tensores que precisam ser explicitamente inicializados e usados no gráfico para manter o estado na sessão. Simplesmente chamando o construtor a variável é adicionada no gráfico computacional.
As variáveis são especialmente úteis quando você começa com os modelos de treinamento e são usadas para manter e atualizar parâmetros. Um valor inicial passado como argumento de um construtor representa um tensor ou objeto que pode ser convertido ou retornado como um tensor. Isso significa que se quisermos preencher uma variável com alguns valores predefinidos ou aleatórios para serem usados posteriormente no processo de treinamento e atualizados ao longo de iterações, podemos defini-la da seguinte maneira:
k = tf.Variable(tf.zeros([1]), name="k")Outra maneira de usar variáveis no TensorFlow é em cálculos em que essa variável não é treinável e pode ser definida da seguinte maneira:
k = tf.Variable(tf.add(a, b), trainable=False)Sessões
Para realmente avaliar os nós, devemos executar um gráfico computacional dentro de uma sessão.
Uma sessão encapsula o controle e o estado do tempo de execução do TensorFlow. Uma sessão sem parâmetros usará o gráfico padrão criado na sessão atual, caso contrário a classe de sessão aceita um parâmetro de gráfico, que é usado nessa sessão para ser executado.
Abaixo está um breve trecho de código que mostra como os termos definidos acima podem ser usados no TensorFlow para calcular uma função linear simples.
import tensorflow as tf x = tf.constant(-2.0, name="x", dtype=tf.float32) a = tf.constant(5.0, name="a", dtype=tf.float32) b = tf.constant(13.0, name="b", dtype=tf.float32) y = tf.Variable(tf.add(tf.multiply(a, x), b)) init = tf.global_variables_initializer() with tf.Session() as session: session.run(init) print session.run(y)Usando o TensorFlow: definindo gráficos computacionais
O bom de trabalhar com gráficos de fluxo de dados é que o modelo de execução é separado de sua execução (na CPU, GPU ou alguma combinação) onde, uma vez implementado, o software no TensorFlow pode ser usado na CPU ou GPU onde toda a complexidade relacionada ao código execução está oculta.
O gráfico de computação pode ser criado no processo de uso da biblioteca TensorFlow sem precisar instanciar explicitamente os objetos Graph.
Um objeto Graph no TensorFlow pode ser criado como resultado de uma simples linha de código como c = tf.add(a, b) . Isso criará um nó de operação que recebe dois tensores a e b que produzem sua soma c como saída.
O gráfico de computação é um processo integrado que usa a biblioteca sem precisar chamar o objeto gráfico diretamente. Um objeto gráfico no TensorFlow, que contém um conjunto de operações e tensores como unidades de dados, é usado entre operações que permitem o mesmo processo e contém mais de um gráfico onde cada gráfico será atribuído a uma sessão diferente. Por exemplo, a linha simples de código c = tf.add(a, b) criará um nó de operação que recebe dois tensores a como entrada c b saída.
O TensorFlow também fornece um mecanismo de alimentação para corrigir um tensor para qualquer operação no gráfico, em que a alimentação substitui a saída de uma operação pelo valor do tensor. Os dados do feed são passados como um argumento na chamada da função run() .
Um espaço reservado é a maneira do TensorFlow de permitir que os desenvolvedores injetem dados no gráfico de computação por meio de espaços reservados que são vinculados a algumas expressões. A assinatura do placeholder é:
placeholder(dtype, shape=None, name=None)onde dtype é o tipo de elementos nos tensores e pode fornecer tanto a forma dos tensores a serem alimentados quanto o nome da operação.
Se a forma não for passada, este tensor pode ser alimentado com qualquer forma. Uma observação importante é que o tensor placeholder tem que ser alimentado com dados, caso contrário, ao executar a sessão e se essa parte estiver faltando, o placeholder gera um erro com a seguinte estrutura:
InvalidArgumentError (see above for traceback): You must feed a value for placeholder tensor 'y' with dtype floatA vantagem dos placeholders é que eles permitem que os desenvolvedores criem operações, e o gráfico computacional em geral, sem a necessidade de fornecer os dados antecipadamente para isso, e os dados podem ser adicionados em tempo de execução a partir de fontes externas.
Vamos pegar um problema simples de multiplicar dois inteiros x e y no modo TensorFlow, onde um espaço reservado será usado junto com um mecanismo de alimentação por meio do método de run de sessão.
import tensorflow as tf x = tf.placeholder(tf.float32, name="x") y = tf.placeholder(tf.float32, name="y") z = tf.multiply(x, y, name="z") with tf.Session() as session: print session.run(z, feed_dict={x: 2.1, y: 3.0})Visualizando o gráfico computacional com o TensorBoard
O TensorBoard é uma ferramenta de visualização para analisar gráficos de fluxo de dados. Isso pode ser útil para obter uma melhor compreensão dos modelos de aprendizado de máquina.
Com o TensorBoard, você pode obter informações sobre diferentes tipos de estatísticas sobre os parâmetros e detalhes sobre as partes do gráfico computacional em geral. Não é incomum que uma rede neural profunda tenha um grande número de nós. O TensorBoard permite que os desenvolvedores obtenham informações sobre cada nó e como a computação é executada no tempo de execução do TensorFlow.
Agora vamos voltar ao nosso exemplo do início deste tutorial do TensorFlow, onde definimos uma função linear com o formato y = a*x + b .
Para registrar eventos da sessão que podem ser usados posteriormente no TensorBoard, o TensorFlow fornece a classe FileWriter . Ele pode ser usado para criar um arquivo de evento para armazenar resumos onde o construtor aceita seis parâmetros e se parece com:
__init__(logdir, graph=None, max_queue=10, flush_secs=120, graph_def=None, filename_suffix=None)onde o parâmetro logdir é obrigatório e outros possuem valores padrão. O parâmetro gráfico será passado do objeto de sessão criado no programa de treinamento. O código de exemplo completo se parece com:
import tensorflow as tf x = tf.constant(-2.0, name="x", dtype=tf.float32) a = tf.constant(5.0, name="a", dtype=tf.float32) b = tf.constant(13.0, name="b", dtype=tf.float32) y = tf.Variable(tf.add(tf.multiply(a, x), b)) init = tf.global_variables_initializer() with tf.Session() as session: merged = tf.summary.merge_all() // new writer = tf.summary.FileWriter("logs", session.graph) // new session.run(init) print session.run(y) Adicionamos apenas duas novas linhas. Nós mesclamos todos os resumos coletados no gráfico padrão e o FileWriter é usado para despejar eventos no arquivo conforme descrito acima, respectivamente.
Após executar o programa, temos o arquivo no diretório logs, e o último passo é executar o tensorboard :
tensorboard --logdir logs/ Agora o TensorBoard está iniciado e rodando na porta padrão 6006. Após abrir http://localhost:6006 e clicar no item de menu Graphs (localizado na parte superior da página), você poderá ver o gráfico, como este na imagem abaixo:
O TensorBoard marca constantes e símbolos específicos de nós de resumo, descritos abaixo.
Matemática com TensorFlow
Os tensores são as estruturas de dados básicas no TensorFlow e representam as arestas de conexão em um gráfico de fluxo de dados.
Um tensor simplesmente identifica uma matriz ou lista multidimensional. A estrutura tensorial pode ser identificada com três parâmetros: classificação, forma e tipo.
- Rank: Identifica o número de dimensões do tensor. Um posto é conhecido como a ordem ou n-dimensões de um tensor, onde, por exemplo, o tensor de posto 1 é um vetor ou o tensor de posto 2 é uma matriz.
- Forma: A forma de um tensor é o número de linhas e colunas que ele possui.
- Tipo: O tipo de dados atribuído aos elementos tensores.
Para construir um tensor no TensorFlow, podemos construir um array n-dimensional. Isso pode ser feito facilmente usando a biblioteca NumPy ou convertendo uma matriz n-dimensional do Python em um tensor TensorFlow.
Para construir um tensor 1-d, usaremos um array NumPy, que construiremos passando uma lista Python embutida.
import numpy as np tensor_1d = np.array([1.45, -1, 0.2, 102.1])Trabalhar com esse tipo de array é semelhante a trabalhar com uma lista interna do Python. A principal diferença é que a matriz NumPy também contém algumas propriedades adicionais, como dimensão, forma e tipo.
> > print tensor1d [ 1.45 -1. 0.2 102.1 ] > > print tensor1d[0] 1.45 > > print tensor1d[2] 0.2 > > print tensor1d.ndim 1 > > print tensor1d.shape (4,) > > print tensor1d.dtype float64Um array NumPy pode ser facilmente convertido em um tensor TensorFlow com a função auxiliar convert_to_tensor, que ajuda os desenvolvedores a converter objetos Python em objetos tensores. Esta função aceita objetos tensores, arrays NumPy, listas Python e escalares Python.
tensor = tf.convert_to_tensor(tensor_1d, dtype=tf.float64)Agora, se vincularmos nosso tensor à sessão do TensorFlow, poderemos ver os resultados de nossa conversão.
tensor = tf.convert_to_tensor(tensor_1d, dtype=tf.float64) with tf.Session() as session: print session.run(tensor) print session.run(tensor[0]) print session.run(tensor[1])Saída:
[ 1.45 -1. 0.2 102.1 ] 1.45 -1.0Podemos criar um tensor 2-d, ou matriz, de maneira semelhante:
tensor_2d = np.array(np.random.rand(4, 4), dtype='float32') tensor_2d_1 = np.array(np.random.rand(4, 4), dtype='float32') tensor_2d_2 = np.array(np.random.rand(4, 4), dtype='float32') m1 = tf.convert_to_tensor(tensor_2d) m2 = tf.convert_to_tensor(tensor_2d_1) m3 = tf.convert_to_tensor(tensor_2d_2) mat_product = tf.matmul(m1, m2) mat_sum = tf.add(m2, m3) mat_det = tf.matrix_determinant(m3) with tf.Session() as session: print session.run(mat_product) print session.run(mat_sum) print session.run(mat_det)Operações de tensor
No exemplo acima, apresentamos algumas operações do TensorFlow nos vetores e matrizes. As operações realizam certos cálculos nos tensores. Quais cálculos são esses é mostrado na tabela abaixo.
| Operador do TensorFlow | Descrição |
|---|---|
| tf.adicionar | x+y |
| tf.subtrair | xy |
| tf.multiplicar | x*y |
| tf.div | x/y |
| tf.mod | x % y |
| tf.abs | |x| |
| tf.negativo | -x |
| tf.sign | sinal (x) |
| tf.square | x*x |
| tf.round | rodada (x) |
| tf.sqrt | sqrt(x) |
| tf.pow | x^y |
| tf.exp | e^x |
| tf.log | log(x) |
| tf.máximo | max(x, y) |
| tf.mínimo | min(x, y) |
| tf.cos | cos(x) |
| tf.sin | pecado(x) |
As operações do TensorFlow listadas na tabela acima funcionam com objetos tensores e são executadas por elemento. Portanto, se você quiser calcular o cosseno para um vetor x, a operação TensorFlow fará cálculos para cada elemento no tensor passado.

tensor_1d = np.array([0, 0, 0]) tensor = tf.convert_to_tensor(tensor_1d, dtype=tf.float64) with tf.Session() as session: print session.run(tf.cos(tensor))Saída:
[ 1. 1. 1.]Operações de Matriz
As operações de matriz são muito importantes para modelos de aprendizado de máquina, como regressão linear, pois são frequentemente usadas neles. O TensorFlow suporta todas as operações de matrizes mais comuns, como multiplicação, transposição, inversão, cálculo do determinante, resolução de equações lineares e muito mais.
A seguir, explicaremos algumas das operações matriciais. Eles tendem a ser importantes quando se trata de modelos de aprendizado de máquina, como na regressão linear. Vamos escrever um código que fará operações básicas com matrizes, como multiplicação, obter a transposição, obter o determinante, multiplicação, sol e muito mais.
Abaixo estão exemplos básicos de como chamar essas operações.
import tensorflow as tf import numpy as np def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) m1 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m2 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m3 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m4 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m5 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m_tranpose = tf.transpose(m1) m_mul = tf.matmul(m1, m2) m_det = tf.matrix_determinant(m3) m_inv = tf.matrix_inverse(m4) m_solve = tf.matrix_solve(m5, [[1], [1], [1], [1]]) with tf.Session() as session: print session.run(m_tranpose) print session.run(m_mul) print session.run(m_inv) print session.run(m_det) print session.run(m_solve)Transformando dados
Redução
O TensorFlow suporta diferentes tipos de redução. A redução é uma operação que remove uma ou mais dimensões de um tensor executando certas operações nessas dimensões. Uma lista de reduções com suporte para a versão atual do TensorFlow pode ser encontrada aqui. Apresentaremos alguns deles no exemplo abaixo.
import tensorflow as tf import numpy as np def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) x = convert( np.array( [ (1, 2, 3), (4, 5, 6), (7, 8, 9) ]), tf.int32) bool_tensor = convert([(True, False, True), (False, False, True), (True, False, False)], tf.bool) red_sum_0 = tf.reduce_sum(x) red_sum = tf.reduce_sum(x, axis=1) red_prod_0 = tf.reduce_prod(x) red_prod = tf.reduce_prod(x, axis=1) red_min_0 = tf.reduce_min(x) red_min = tf.reduce_min(x, axis=1) red_max_0 = tf.reduce_max(x) red_max = tf.reduce_max(x, axis=1) red_mean_0 = tf.reduce_mean(x) red_mean = tf.reduce_mean(x, axis=1) red_bool_all_0 = tf.reduce_all(bool_tensor) red_bool_all = tf.reduce_all(bool_tensor, axis=1) red_bool_any_0 = tf.reduce_any(bool_tensor) red_bool_any = tf.reduce_any(bool_tensor, axis=1) with tf.Session() as session: print "Reduce sum without passed axis parameter: ", session.run(red_sum_0) print "Reduce sum with passed axis=1: ", session.run(red_sum) print "Reduce product without passed axis parameter: ", session.run(red_prod_0) print "Reduce product with passed axis=1: ", session.run(red_prod) print "Reduce min without passed axis parameter: ", session.run(red_min_0) print "Reduce min with passed axis=1: ", session.run(red_min) print "Reduce max without passed axis parameter: ", session.run(red_max_0) print "Reduce max with passed axis=1: ", session.run(red_max) print "Reduce mean without passed axis parameter: ", session.run(red_mean_0) print "Reduce mean with passed axis=1: ", session.run(red_mean) print "Reduce bool all without passed axis parameter: ", session.run(red_bool_all_0) print "Reduce bool all with passed axis=1: ", session.run(red_bool_all) print "Reduce bool any without passed axis parameter: ", session.run(red_bool_any_0) print "Reduce bool any with passed axis=1: ", session.run(red_bool_any)Saída:
Reduce sum without passed axis parameter: 45 Reduce sum with passed axis=1: [ 6 15 24] Reduce product without passed axis parameter: 362880 Reduce product with passed axis=1: [ 6 120 504] Reduce min without passed axis parameter: 1 Reduce min with passed axis=1: [1 4 7] Reduce max without passed axis parameter: 9 Reduce max with passed axis=1: [3 6 9] Reduce mean without passed axis parameter: 5 Reduce mean with passed axis=1: [2 5 8] Reduce bool all without passed axis parameter: False Reduce bool all with passed axis=1: [False False False] Reduce bool any without passed axis parameter: True Reduce bool any with passed axis=1: [ True True True]O primeiro parâmetro dos operadores de redução é o tensor que queremos reduzir. O segundo parâmetro são os índices de dimensões ao longo dos quais queremos realizar a redução. Esse parâmetro é opcional e, se não for passado, a redução será realizada em todas as dimensões.
Podemos dar uma olhada na operação reduce_sum. Passamos um tensor 2-d e queremos reduzi-lo ao longo da dimensão 1.
No nosso caso, a soma resultante seria:
[1 + 2 + 3 = 6, 4 + 5 + 6 = 15, 7 + 8 + 9 = 24]Se passássemos a dimensão 0, o resultado seria:
[1 + 4 + 7 = 12, 2 + 5 + 8 = 15, 3 + 6 + 9 = 18]Se não passarmos nenhum eixo, o resultado será apenas a soma geral de:
1 + 4 + 7 = 12, 2 + 5 + 8 = 15, 3 + 6 + 9 = 45Todas as funções de redução têm uma interface semelhante e estão listadas na documentação de redução do TensorFlow.
Segmentação
A segmentação é um processo em que uma das dimensões é o processo de mapeamento de dimensões em índices de segmento fornecidos e os elementos resultantes são determinados por uma linha de índice.
A segmentação está realmente agrupando os elementos sob índices repetidos, então, por exemplo, no nosso caso, nós segmentamos ids [0, 0, 1, 2, 2] aplicados no tensor tens1 , o que significa que o primeiro e o segundo arrays serão transformados após a segmentação operação (no nosso caso soma) e obterá um novo array, que se parece com (2, 8, 1, 0) = (2+0, 5+3, 3-2, -5+5) . O terceiro elemento no tensor tens1 é intocado porque não está agrupado em nenhum índice repetido, e os dois últimos arrays são somados da mesma forma que foi o caso do primeiro grupo. Além da soma, o TensorFlow oferece suporte a produto, média, máx. e mín.
import tensorflow as tf import numpy as np def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) seg_ids = tf.constant([0, 0, 1, 2, 2]) tens1 = convert(np.array([(2, 5, 3, -5), (0, 3, -2, 5), (4, 3, 5, 3), (6, 1, 4, 0), (6, 1, 4, 0)]), tf.int32) tens2 = convert(np.array([1, 2, 3, 4, 5]), tf.int32) seg_sum = tf.segment_sum(tens1, seg_ids) seg_sum_1 = tf.segment_sum(tens2, seg_ids) with tf.Session() as session: print "Segmentation sum tens1: ", session.run(seg_sum) print "Segmentation sum tens2: ", session.run(seg_sum_1) Segmentation sum tens1: [[ 2 8 1 0] [ 4 3 5 3] [12 2 8 0]] Segmentation sum tens2: [3 3 9]Utilitários de sequência
Os utilitários de sequência incluem métodos como:
- função argmin, que retorna o índice com valor mínimo nos eixos do tensor de entrada,
- função argmax, que retorna o índice com o valor máximo nos eixos do tensor de entrada,
- setdiff, que calcula a diferença entre duas listas de números ou strings,
- onde função, que retornará elementos de dois elementos passados x ou y, que depende da condição passada, ou
- função única, que retornará elementos únicos em um tensor 1-D.
Demonstramos alguns exemplos de execução abaixo:
import numpy as np import tensorflow as tf def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) x = convert(np.array([ [2, 2, 1, 3], [4, 5, 6, -1], [0, 1, 1, -2], [6, 2, 3, 0] ])) y = convert(np.array([1, 2, 5, 3, 7])) z = convert(np.array([1, 0, 4, 6, 2])) arg_min = tf.argmin(x, 1) arg_max = tf.argmax(x, 1) unique = tf.unique(y) diff = tf.setdiff1d(y, z) with tf.Session() as session: print "Argmin = ", session.run(arg_min) print "Argmax = ", session.run(arg_max) print "Unique_values = ", session.run(unique)[0] print "Unique_idx = ", session.run(unique)[1] print "Setdiff_values = ", session.run(diff)[0] print "Setdiff_idx = ", session.run(diff)[1] print session.run(diff)[1]Saída:
Argmin = [2 3 3 3] Argmax = [3 2 1 0] Unique_values = [ 1. 2. 5. 3. 7.] Unique_idx = [0 1 2 3 4] Setdiff_values = [ 5. 3. 7.] Setdiff_idx = [2 3 4]Aprendizado de máquina com TensorFlow
Nesta seção, apresentaremos um caso de uso de aprendizado de máquina com o TensorFlow. O primeiro exemplo será um algoritmo de classificação de dados com a abordagem kNN, e o segundo utilizará o algoritmo de regressão linear.
kNN
O primeiro algoritmo é o k-Nearest Neighbors (kNN). É um algoritmo de aprendizado supervisionado que usa métricas de distância, por exemplo, distância euclidiana, para classificar dados em relação ao treinamento. É um dos algoritmos mais simples, mas ainda muito poderoso para classificar dados. Prós deste algoritmo:
- Dá alta precisão quando o modelo de treinamento é grande o suficiente e
- Geralmente não é sensível a valores discrepantes e não precisamos ter nenhuma suposição sobre os dados.
Contras deste algoritmo:
- Computacionalmente caro e
- Requer muita memória onde novos dados classificados precisam ser adicionados a todas as instâncias de treinamento iniciais.
A distância que usaremos neste exemplo de código é a Euclidiana, que define a distância entre dois pontos assim:
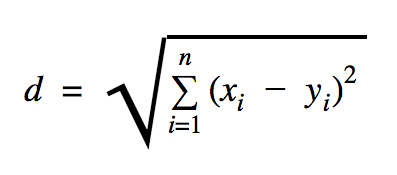
Nesta fórmula, n é o número de dimensões do espaço, x é o vetor dos dados de treinamento e y é um novo ponto de dados que queremos classificar.
import os import numpy as np import tensorflow as tf ccf_train_data = "train_dataset.csv" ccf_test_data = "test_dataset.csv" dataset_dir = os.path.abspath(os.path.join(os.path.dirname(__file__), '../datasets')) ccf_train_filepath = os.path.join(dataset_dir, ccf_train_data) ccf_test_filepath = os.path.join(dataset_dir, ccf_test_data) def load_data(filepath): from numpy import genfromtxt csv_data = genfromtxt(filepath, delimiter=",", skip_header=1) data = [] labels = [] for d in csv_data: data.append(d[:-1]) labels.append(d[-1]) return np.array(data), np.array(labels) train_dataset, train_labels = load_data(ccf_train_filepath) test_dataset, test_labels = load_data(ccf_test_filepath) train_pl = tf.placeholder("float", [None, 28]) test_pl = tf.placeholder("float", [28]) knn_prediction = tf.reduce_sum(tf.abs(tf.add(train_pl, tf.negative(test_pl))), axis=1) pred = tf.argmin(knn_prediction, 0) with tf.Session() as tf_session: missed = 0 for i in xrange(len(test_dataset)): knn_index = tf_session.run(pred, feed_dict={train_pl: train_dataset, test_pl: test_dataset[i]}) print "Predicted class {} -- True class {}".format(train_labels[knn_index], test_labels[i]) if train_labels[knn_index] != test_labels[i]: missed += 1 tf.summary.FileWriter("../samples/article/logs", tf_session.graph) print "Missed: {} -- Total: {}".format(missed, len(test_dataset))O conjunto de dados que usamos no exemplo acima é aquele que pode ser encontrado na seção de conjuntos de dados do Kaggle. Usamos aquele que contém transações feitas por cartões de crédito de titulares de cartões europeus. Estamos usando os dados sem nenhuma limpeza ou filtragem e, de acordo com a descrição no Kaggle para este conjunto de dados, é altamente desequilibrado. O conjunto de dados contém 31 variáveis: Time, V1, …, V28, Amount e Class. Neste exemplo de código, usamos apenas V1, …, V28 e Class. A classe rotula as transações fraudulentas com 1 e as que não são com 0.
A amostra de código contém principalmente as coisas que descrevemos nas seções anteriores, com exceção de onde introduzimos a função para carregar um conjunto de dados. A função load_data(filepath) receberá um arquivo CSV como argumento e retornará uma tupla com dados e rótulos definidos em CSV.
Logo abaixo dessa função, definimos espaços reservados para os dados de teste e treinados. Os dados treinados são usados no modelo de previsão para resolver os rótulos dos dados de entrada que precisam ser classificados. No nosso caso, kNN usa a distância euclidiana para obter o rótulo mais próximo.
A taxa de erro pode ser calculada por divisão simples com o número quando um classificador falhou pelo número total de exemplos que no nosso caso para este conjunto de dados é 0,2 (ou seja, o classificador nos dá o rótulo de dados errado para 20% dos dados de teste).
Regressão linear
O algoritmo de regressão linear procura uma relação linear entre duas variáveis. Se rotularmos a variável dependente como y e a variável independente como x, estamos tentando estimar os parâmetros da função y = Wx + b .
A regressão linear é um algoritmo amplamente utilizado no campo das ciências aplicadas. Este algoritmo permite adicionar na implementação dois conceitos importantes de aprendizado de máquina: a função de custo e o método de gradiente descendente para encontrar o mínimo da função.
Um algoritmo de aprendizado de máquina implementado usando esse método deve prever valores de y em função de x , onde um algoritmo de regressão linear determinará os valores W e b , que na verdade são desconhecidos e que são determinados ao longo do processo de treinamento. Uma função de custo é escolhida, e geralmente o erro quadrático médio é usado onde o gradiente descendente é o algoritmo de otimização usado para encontrar um mínimo local da função de custo.
O método gradiente descendente é apenas um mínimo de função local, mas pode ser usado na busca de um mínimo global escolhendo aleatoriamente um novo ponto de partida uma vez encontrado um mínimo local e repetindo esse processo muitas vezes. Se o número de mínimos da função for limitado e houver um número muito alto de tentativas, há uma boa chance de que em algum momento o mínimo global seja detectado. Mais alguns detalhes sobre esta técnica deixaremos para o artigo que mencionamos na seção de introdução.
import tensorflow as tf import numpy as np test_data_size = 2000 iterations = 10000 learn_rate = 0.005 def generate_test_values(): train_x = [] train_y = [] for _ in xrange(test_data_size): x1 = np.random.rand() x2 = np.random.rand() x3 = np.random.rand() y_f = 2 * x1 + 3 * x2 + 7 * x3 + 4 train_x.append([x1, x2, x3]) train_y.append(y_f) return np.array(train_x), np.transpose([train_y]) x = tf.placeholder(tf.float32, [None, 3], name="x") W = tf.Variable(tf.zeros([3, 1]), name="W") b = tf.Variable(tf.zeros([1]), name="b") y = tf.placeholder(tf.float32, [None, 1]) model = tf.add(tf.matmul(x, W), b) cost = tf.reduce_mean(tf.square(y - model)) train = tf.train.GradientDescentOptimizer(learn_rate).minimize(cost) train_dataset, train_values = generate_test_values() init = tf.global_variables_initializer() with tf.Session() as session: session.run(init) for _ in xrange(iterations): session.run(train, feed_dict={ x: train_dataset, y: train_values }) print "cost = {}".format(session.run(cost, feed_dict={ x: train_dataset, y: train_values })) print "W = {}".format(session.run(W)) print "b = {}".format(session.run(b))Saída:
cost = 3.1083032809e-05 W = [[ 1.99049103] [ 2.9887135 ] [ 6.98754263]] b = [ 4.01742554] No exemplo acima, temos duas novas variáveis, que chamamos de cost e train . Com essas duas variáveis, definimos um otimizador que queremos usar em nosso modelo de treinamento e a função que queremos minimizar.
Ao final, os parâmetros de saída de W e b devem ser idênticos aos definidos na função generate_test_values . Na linha 17, na verdade definimos uma função que usamos para gerar os pontos de dados lineares para treinar onde w1=2 , w2=3 , w3=7 e b=4 . A regressão linear do exemplo acima é multivariada onde mais de uma variável independente é usada.
Conclusão
Como você pode ver neste tutorial do TensorFlow, o TensorFlow é uma estrutura poderosa que facilita muito o trabalho com expressões matemáticas e matrizes multidimensionais, algo fundamentalmente necessário no aprendizado de máquina. Ele também abstrai as complexidades de executar os gráficos de dados e dimensionar.
Com o tempo, o TensorFlow cresceu em popularidade e agora está sendo usado por desenvolvedores para resolver problemas usando métodos de aprendizado profundo para reconhecimento de imagem, detecção de vídeo, processamento de texto como análise de sentimentos etc. Como qualquer outra biblioteca, você pode precisar de algum tempo para se acostumar aos conceitos em que o TensorFlow foi desenvolvido. E, depois de fazer isso, com a ajuda da documentação e do suporte da comunidade, representar problemas como gráficos de dados e resolvê-los com o TensorFlow pode tornar o aprendizado de máquina em escala um processo menos tedioso.
