Pierwsze kroki z TensorFlow: samouczek dotyczący uczenia maszynowego
Opublikowany: 2022-03-11TensorFlow to biblioteka oprogramowania typu open source stworzona przez Google, która służy do wdrażania systemów uczenia maszynowego i głębokiego uczenia się. Te dwie nazwy zawierają szereg potężnych algorytmów, które mają wspólne wyzwanie — pozwalają komputerowi nauczyć się automatycznie wykrywać złożone wzorce i/lub podejmować najlepsze możliwe decyzje.
Jeśli interesują Cię szczegółowe informacje na temat tych systemów, możesz dowiedzieć się więcej z wpisów na blogu Toptal dotyczących uczenia maszynowego i uczenia głębokiego.
Sercem TensorFlow jest biblioteka do programowania przepływu danych. Wykorzystuje różne techniki optymalizacji, aby obliczenia wyrażeń matematycznych były łatwiejsze i bardziej wydajne.
Niektóre z kluczowych cech TensorFlow to:
- Wydajnie pracuje z wyrażeniami matematycznymi obejmującymi tablice wielowymiarowe
- Dobre wsparcie głębokich sieci neuronowych i koncepcji uczenia maszynowego
- Obliczenia na GPU/CPU, gdzie ten sam kod może być wykonywany na obu architekturach
- Wysoka skalowalność obliczeń na różnych maszynach i ogromnych zestawach danych
Razem te cechy sprawiają, że TensorFlow jest idealną platformą dla inteligencji maszyn na skalę produkcyjną.
W tym samouczku TensorFlow dowiesz się, jak korzystać z prostych, ale potężnych metod uczenia maszynowego w TensorFlow oraz jak korzystać z niektórych jego bibliotek pomocniczych do debugowania, wizualizacji i dostrajania utworzonych za jego pomocą modeli.
Instalowanie TensorFlow
Będziemy używać interfejsu API TensorFlow Python, który współpracuje z Python 2.7 i Python 3.3+. Wersja GPU (tylko Linux) wymaga Cuda Toolkit 7.0+ i cuDNN v2+.
Do instalacji TensorFlow użyjemy systemu zarządzania zależnościami pakietów Conda. Conda pozwala nam na oddzielenie wielu środowisk na maszynie. Tutaj dowiesz się, jak zainstalować Condę.
Po zainstalowaniu Condy możemy stworzyć środowisko, które wykorzystamy do instalacji i użytkowania TensorFlow. Poniższe polecenie utworzy nasze środowisko z kilkoma dodatkowymi bibliotekami, takimi jak NumPy, co jest bardzo przydatne, gdy zaczniemy korzystać z TensorFlow.
Wersja Pythona zainstalowana w tym środowisku to 2.7 i użyjemy tej wersji w tym artykule.
conda create --name TensorflowEnv biopython Aby to ułatwić, instalujemy tutaj biopythona zamiast samego NumPy. Obejmuje to NumPy i kilka innych pakietów, których będziemy potrzebować. Zawsze możesz zainstalować pakiety zgodnie z potrzebami za pomocą conda install lub pip install .
Poniższe polecenie aktywuje utworzone środowisko Conda. Będziemy mogli korzystać z zainstalowanych w nim pakietów, bez mieszania z pakietami, które są instalowane globalnie lub w niektórych innych środowiskach.
source activate TensorFlowEnvNarzędzie do instalacji pip jest standardową częścią środowiska Conda. Wykorzystamy go do zainstalowania biblioteki TensorFlow. Zanim to zrobisz, dobrym pierwszym krokiem jest zaktualizowanie pip do najnowszej wersji za pomocą następującego polecenia:
pip install --upgrade pipTeraz jesteśmy gotowi do zainstalowania TensorFlow, uruchamiając:
pip install tensorflowPobieranie i kompilacja TensorFlow może zająć kilka minut. W chwili pisania tego tekstu instaluje TensorFlow 1.1.0.
Wykresy przepływu danych
W TensorFlow obliczenia są opisane za pomocą wykresów przepływu danych. Każdy węzeł wykresu reprezentuje wystąpienie operacji matematycznej (takiej jak dodawanie, dzielenie lub mnożenie), a każda krawędź jest wielowymiarowym zbiorem danych (tensor), na którym wykonywane są operacje.
Ponieważ TensorFlow współpracuje z wykresami obliczeniowymi, są one zarządzane w taki sposób, że każdy węzeł reprezentuje wystąpienie operacji, w której każda operacja ma zero lub więcej wejść i zero lub więcej wyjść.
Krawędzie w TensorFlow można pogrupować w dwie kategorie: Normalne krawędzie przesyłają strukturę danych (tensory), gdzie możliwe jest, że dane wyjściowe jednej operacji stają się danymi wejściowymi dla innej operacji oraz krawędzie specjalne, które służą do kontrolowania zależności między dwoma węzłami, aby ustawić kolejność działania, w której jeden węzeł czeka na zakończenie innego.
Proste wyrażenia
Zanim przejdziemy do omówienia elementów TensorFlow, najpierw przeprowadzimy sesję pracy z TensorFlow, aby poczuć, jak wygląda program TensorFlow.
Zacznijmy od prostych wyrażeń i załóżmy, że z jakiegoś powodu chcemy obliczyć funkcję y = 5*x + 13 w stylu TensorFlow.
W prostym kodzie Pythona wyglądałoby to tak:
x = -2.0 y = 5*x + 13 print yco daje nam w tym przypadku wynik 3.0.
Teraz skonwertujemy powyższe wyrażenie na wyrażenia TensorFlow.
Stałe
W TensorFlow stałe są tworzone przy użyciu stałej funkcji, która ma constant(value, dtype=None, shape=None, name='Const', verify_shape=False) , gdzie value jest rzeczywistą wartością stałej, która będzie używana w dalsze obliczenia, dtype to parametr typu danych (np. float32/64, int8/16 itp.), shape to opcjonalne wymiary, name to opcjonalna nazwa tensora, a ostatni parametr to wartość logiczna, która wskazuje na weryfikację kształt wartości.
Jeśli potrzebujesz stałych z określonymi wartościami w modelu treningowym, obiekt constant może być użyty, jak w poniższym przykładzie:
z = tf.constant(5.2, name="x", dtype=tf.float32)Zmienne
Zmienne w TensorFlow to bufory w pamięci zawierające tensory, które muszą być jawnie zainicjowane i użyte w grafie, aby utrzymać stan w całej sesji. Poprzez proste wywołanie konstruktora zmienna jest dodawana do wykresu obliczeniowego.
Zmienne są szczególnie przydatne po rozpoczęciu pracy z modelami uczącymi i służą do przechowywania i aktualizowania parametrów. Wartość początkowa przekazana jako argument konstruktora reprezentuje tensor lub obiekt, który może zostać przekonwertowany lub zwrócony jako tensor. Oznacza to, że jeśli chcemy wypełnić zmienną pewnymi predefiniowanymi lub losowymi wartościami, które będą później używane w procesie uczenia i aktualizowane przez iteracje, możemy to zdefiniować w następujący sposób:
k = tf.Variable(tf.zeros([1]), name="k")Innym sposobem wykorzystania zmiennych w TensorFlow są obliczenia, w których tej zmiennej nie można wytrenować i można ją zdefiniować w następujący sposób:
k = tf.Variable(tf.add(a, b), trainable=False)Sesje
Aby faktycznie ocenić węzły, musimy uruchomić wykres obliczeniowy w ramach sesji.
Sesja zawiera kontrolę i stan środowiska uruchomieniowego TensorFlow. Sesja bez parametrów użyje domyślnego wykresu utworzonego w bieżącej sesji, w przeciwnym razie klasa sesji zaakceptuje do wykonania parametr wykresu, który jest używany w tej sesji.
Poniżej znajduje się krótki fragment kodu, który pokazuje, w jaki sposób zdefiniowane powyżej terminy mogą być używane w TensorFlow do obliczania prostej funkcji liniowej.
import tensorflow as tf x = tf.constant(-2.0, name="x", dtype=tf.float32) a = tf.constant(5.0, name="a", dtype=tf.float32) b = tf.constant(13.0, name="b", dtype=tf.float32) y = tf.Variable(tf.add(tf.multiply(a, x), b)) init = tf.global_variables_initializer() with tf.Session() as session: session.run(init) print session.run(y)Korzystanie z TensorFlow: definiowanie wykresów obliczeniowych
Dobrą rzeczą w pracy z wykresami przepływu danych jest to, że model wykonania jest oddzielony od jego wykonania (na CPU, GPU lub jakiejś kombinacji), gdzie po wdrożeniu oprogramowanie w TensorFlow może być używane na CPU lub GPU, gdzie cała złożoność związana z kodem wykonanie jest ukryte.
Wykres obliczeniowy można zbudować w procesie korzystania z biblioteki TensorFlow bez konieczności jawnego tworzenia instancji obiektów Graph.
Obiekt Graph w TensorFlow można utworzyć w wyniku prostej linii kodu, takiej jak c = tf.add(a, b) . Stworzy to węzeł operacji, który pobiera dwa tensory a i b , które dają sumę c jako wynik.
Graf obliczeniowy to wbudowany proces, który korzysta z biblioteki bez konieczności bezpośredniego wywoływania obiektu grafu. Obiekt wykresu w TensorFlow, który zawiera zestaw operacji i tensorów jako jednostki danych, jest używany między operacjami, co umożliwia ten sam proces i zawiera więcej niż jeden wykres, przy czym każdy wykres zostanie przypisany do innej sesji. Na przykład prosty wiersz kodu c = tf.add(a, b) b a dane wejściowe i generuje ich sumę c jako dane wyjściowe.
TensorFlow zapewnia również mechanizm posuwu, który umożliwia łatanie tensora dowolnej operacji na wykresie, w którym posuw zastępuje dane wyjściowe operacji wartością tensora. Dane kanału są przekazywane jako argument w wywołaniu funkcji run() .
Symbol zastępczy to sposób TensorFlow na umożliwienie programistom wstrzykiwanie danych do wykresu obliczeniowego za pomocą symboli zastępczych, które są powiązane wewnątrz niektórych wyrażeń. Podpis osoby zastępczej to:
placeholder(dtype, shape=None, name=None)gdzie dtype jest typem elementów w tensorach i może zapewnić zarówno kształt tensorów, które mają zostać podane, jak i nazwę operacji.
Jeśli kształt nie zostanie przekazany, ten tensor może być zasilany dowolnym kształtem. Ważną informacją jest to, że tensor symbolu zastępczego musi zostać zasilony danymi, w przeciwnym razie po wykonaniu sesji i jeśli tej części brakuje, symbol zastępczy generuje błąd o następującej strukturze:
InvalidArgumentError (see above for traceback): You must feed a value for placeholder tensor 'y' with dtype floatZaletą symboli zastępczych jest to, że umożliwiają programistom tworzenie operacji i ogólnie grafu obliczeniowego bez konieczności wcześniejszego dostarczania danych, a dane można dodawać w czasie wykonywania ze źródeł zewnętrznych.
Weźmy prosty problem polegający na pomnożeniu dwóch liczb całkowitych x w sposób y , gdzie symbol zastępczy będzie używany wraz z mechanizmem podawania poprzez metodę run sesji.
import tensorflow as tf x = tf.placeholder(tf.float32, name="x") y = tf.placeholder(tf.float32, name="y") z = tf.multiply(x, y, name="z") with tf.Session() as session: print session.run(z, feed_dict={x: 2.1, y: 3.0})Wizualizacja grafu obliczeniowego za pomocą TensorBoard
TensorBoard to narzędzie do wizualizacji służące do analizy wykresów przepływu danych. Może to być przydatne do lepszego zrozumienia modeli uczenia maszynowego.
Dzięki TensorBoard możesz uzyskać wgląd w różne rodzaje statystyk dotyczących parametrów i ogólnie szczegóły dotyczące części wykresu obliczeniowego. Nie jest niczym niezwykłym, że głęboka sieć neuronowa ma dużą liczbę węzłów. TensorBoard pozwala programistom uzyskać wgląd w każdy węzeł i sposób wykonywania obliczeń w środowisku wykonawczym TensorFlow.
Wróćmy teraz do naszego przykładu z początku tego samouczka TensorFlow, w którym zdefiniowaliśmy funkcję liniową w formacie y = a*x + b .
W celu rejestrowania zdarzeń z sesji, które później można wykorzystać w TensorBoard, TensorFlow udostępnia klasę FileWriter . Można go wykorzystać do stworzenia pliku zdarzeń do przechowywania podsumowań, gdzie konstruktor akceptuje sześć parametrów i wygląda następująco:
__init__(logdir, graph=None, max_queue=10, flush_secs=120, graph_def=None, filename_suffix=None)gdzie parametr logdir jest wymagany, a inne mają wartości domyślne. Parametr wykresu zostanie przekazany z obiektu sesji utworzonego w programie szkoleniowym. Pełny przykładowy kod wygląda następująco:
import tensorflow as tf x = tf.constant(-2.0, name="x", dtype=tf.float32) a = tf.constant(5.0, name="a", dtype=tf.float32) b = tf.constant(13.0, name="b", dtype=tf.float32) y = tf.Variable(tf.add(tf.multiply(a, x), b)) init = tf.global_variables_initializer() with tf.Session() as session: merged = tf.summary.merge_all() // new writer = tf.summary.FileWriter("logs", session.graph) // new session.run(init) print session.run(y) Dodaliśmy tylko dwie nowe linie. Łączymy wszystkie podsumowania zebrane na domyślnym wykresie, a FileWriter służy do zrzucania zdarzeń do pliku, odpowiednio, jak opisano powyżej.
Po uruchomieniu programu mamy plik w logach katalogu, a ostatnim krokiem jest uruchomienie tensorboard :
tensorboard --logdir logs/ Teraz TensorBoard jest uruchomiony i działa na domyślnym porcie 6006. Po otwarciu http://localhost:6006 i kliknięciu pozycji menu Wykresy (znajdującej się na górze strony), będziesz mógł zobaczyć wykres, taki jak ten na zdjęciu poniżej:
TensorBoard oznacza stałe i symbole poszczególnych węzłów podsumowujących, które opisano poniżej.
Matematyka z TensorFlow
Tensory to podstawowe struktury danych w TensorFlow i reprezentują krawędzie łączące na wykresie przepływu danych.
Tensor po prostu identyfikuje wielowymiarową tablicę lub listę. Strukturę tensorową można zidentyfikować za pomocą trzech parametrów: rangi, kształtu i typu.
- Ranga: określa liczbę wymiarów tensora. Rząd jest znany jako rząd lub n-wymiarów tensora, gdzie na przykład tensor rzędu 1 jest wektorem, a tensor rzędu 2 jest macierzą.
- Kształt: kształt tensora to liczba jego wierszy i kolumn.
- Typ: typ danych przypisany do elementów tensorowych.
Aby zbudować tensor w TensorFlow, możemy zbudować tablicę n-wymiarową. Można to łatwo zrobić, korzystając z biblioteki NumPy lub konwertując n-wymiarową tablicę Pythona na tensor TensorFlow.
Aby zbudować tensor jednowymiarowy, użyjemy tablicy NumPy, którą zbudujemy, przekazując wbudowaną listę Pythona.
import numpy as np tensor_1d = np.array([1.45, -1, 0.2, 102.1])Praca z tego rodzaju tablicą jest podobna do pracy z wbudowaną listą Pythona. Główna różnica polega na tym, że tablica NumPy zawiera również dodatkowe właściwości, takie jak wymiar, kształt i typ.
> > print tensor1d [ 1.45 -1. 0.2 102.1 ] > > print tensor1d[0] 1.45 > > print tensor1d[2] 0.2 > > print tensor1d.ndim 1 > > print tensor1d.shape (4,) > > print tensor1d.dtype float64Tablicę NumPy można łatwo przekształcić w tensor TensorFlow za pomocą funkcji pomocniczej convert_to_tensor, która pomaga programistom konwertować obiekty Pythona na obiekty tensorowe. Ta funkcja akceptuje obiekty tensorowe, tablice NumPy, listy Pythona i skalary Pythona.
tensor = tf.convert_to_tensor(tensor_1d, dtype=tf.float64)Teraz, jeśli połączymy nasz tensor z sesją TensorFlow, będziemy mogli zobaczyć wyniki naszej konwersji.
tensor = tf.convert_to_tensor(tensor_1d, dtype=tf.float64) with tf.Session() as session: print session.run(tensor) print session.run(tensor[0]) print session.run(tensor[1])Wyjście:
[ 1.45 -1. 0.2 102.1 ] 1.45 -1.0W podobny sposób możemy stworzyć tensor dwuwymiarowy, czyli macierz:
tensor_2d = np.array(np.random.rand(4, 4), dtype='float32') tensor_2d_1 = np.array(np.random.rand(4, 4), dtype='float32') tensor_2d_2 = np.array(np.random.rand(4, 4), dtype='float32') m1 = tf.convert_to_tensor(tensor_2d) m2 = tf.convert_to_tensor(tensor_2d_1) m3 = tf.convert_to_tensor(tensor_2d_2) mat_product = tf.matmul(m1, m2) mat_sum = tf.add(m2, m3) mat_det = tf.matrix_determinant(m3) with tf.Session() as session: print session.run(mat_product) print session.run(mat_sum) print session.run(mat_det)Operacje tensorowe
W powyższym przykładzie wprowadzimy kilka operacji TensorFlow na wektorach i macierzach. Operacje wykonują pewne obliczenia na tensorach. Jakie są to obliczenia, pokazano w poniższej tabeli.
| Operator TensorFlow | Opis |
|---|---|
| tf.dodaj | x+y |
| tf.odejmuj | xy |
| tf.mnożenie | x*y |
| tf.div | x/y |
| tf.mod | x % y |
| tf.abs | |x| |
| tf.negatywny | -x |
| tf.znak | znak(x) |
| tf.kwadrat | x*x |
| tf.okrągły | okrągły(x) |
| tf.sqrt | sqrt(x) |
| tf.pow | x^y |
| tf.exp | e^x |
| tf.log | log(x) |
| tf.maksimum | maks. (x, y) |
| tf.minimum | min(x, y) |
| tf.cos | cos(x) |
| tf.sin | grzech(x) |
Operacje TensorFlow wymienione w powyższej tabeli działają z obiektami tensorowymi i są wykonywane z uwzględnieniem elementów. Jeśli więc chcesz obliczyć cosinus dla wektora x, operacja TensorFlow wykona obliczenia dla każdego elementu w przekazanym tensorze.

tensor_1d = np.array([0, 0, 0]) tensor = tf.convert_to_tensor(tensor_1d, dtype=tf.float64) with tf.Session() as session: print session.run(tf.cos(tensor))Wyjście:
[ 1. 1. 1.]Operacje na macierzach
Operacje na macierzach są bardzo ważne dla modeli uczenia maszynowego, takich jak regresja liniowa, ponieważ są w nich często używane. TensorFlow obsługuje wszystkie najpopularniejsze operacje na macierzach, takie jak mnożenie, transpozycja, odwracanie, obliczanie wyznacznika, rozwiązywanie równań liniowych i wiele innych.
Następnie wyjaśnimy niektóre operacje na macierzach. Zwykle są ważne, jeśli chodzi o modele uczenia maszynowego, takie jak regresja liniowa. Napiszmy kod, który wykona podstawowe operacje na macierzach, takie jak mnożenie, pobieranie transpozycji, pobieranie wyznacznika, mnożenie, sol i wiele innych.
Poniżej znajdują się podstawowe przykłady wywoływania tych operacji.
import tensorflow as tf import numpy as np def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) m1 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m2 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m3 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m4 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m5 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m_tranpose = tf.transpose(m1) m_mul = tf.matmul(m1, m2) m_det = tf.matrix_determinant(m3) m_inv = tf.matrix_inverse(m4) m_solve = tf.matrix_solve(m5, [[1], [1], [1], [1]]) with tf.Session() as session: print session.run(m_tranpose) print session.run(m_mul) print session.run(m_inv) print session.run(m_det) print session.run(m_solve)Przekształcanie danych
Zmniejszenie
TensorFlow obsługuje różne rodzaje redukcji. Redukcja to operacja, która usuwa jeden lub więcej wymiarów z tensora, wykonując określone operacje na tych wymiarach. Listę obsługiwanych redukcji dla bieżącej wersji TensorFlow można znaleźć tutaj. Kilka z nich przedstawimy w poniższym przykładzie.
import tensorflow as tf import numpy as np def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) x = convert( np.array( [ (1, 2, 3), (4, 5, 6), (7, 8, 9) ]), tf.int32) bool_tensor = convert([(True, False, True), (False, False, True), (True, False, False)], tf.bool) red_sum_0 = tf.reduce_sum(x) red_sum = tf.reduce_sum(x, axis=1) red_prod_0 = tf.reduce_prod(x) red_prod = tf.reduce_prod(x, axis=1) red_min_0 = tf.reduce_min(x) red_min = tf.reduce_min(x, axis=1) red_max_0 = tf.reduce_max(x) red_max = tf.reduce_max(x, axis=1) red_mean_0 = tf.reduce_mean(x) red_mean = tf.reduce_mean(x, axis=1) red_bool_all_0 = tf.reduce_all(bool_tensor) red_bool_all = tf.reduce_all(bool_tensor, axis=1) red_bool_any_0 = tf.reduce_any(bool_tensor) red_bool_any = tf.reduce_any(bool_tensor, axis=1) with tf.Session() as session: print "Reduce sum without passed axis parameter: ", session.run(red_sum_0) print "Reduce sum with passed axis=1: ", session.run(red_sum) print "Reduce product without passed axis parameter: ", session.run(red_prod_0) print "Reduce product with passed axis=1: ", session.run(red_prod) print "Reduce min without passed axis parameter: ", session.run(red_min_0) print "Reduce min with passed axis=1: ", session.run(red_min) print "Reduce max without passed axis parameter: ", session.run(red_max_0) print "Reduce max with passed axis=1: ", session.run(red_max) print "Reduce mean without passed axis parameter: ", session.run(red_mean_0) print "Reduce mean with passed axis=1: ", session.run(red_mean) print "Reduce bool all without passed axis parameter: ", session.run(red_bool_all_0) print "Reduce bool all with passed axis=1: ", session.run(red_bool_all) print "Reduce bool any without passed axis parameter: ", session.run(red_bool_any_0) print "Reduce bool any with passed axis=1: ", session.run(red_bool_any)Wyjście:
Reduce sum without passed axis parameter: 45 Reduce sum with passed axis=1: [ 6 15 24] Reduce product without passed axis parameter: 362880 Reduce product with passed axis=1: [ 6 120 504] Reduce min without passed axis parameter: 1 Reduce min with passed axis=1: [1 4 7] Reduce max without passed axis parameter: 9 Reduce max with passed axis=1: [3 6 9] Reduce mean without passed axis parameter: 5 Reduce mean with passed axis=1: [2 5 8] Reduce bool all without passed axis parameter: False Reduce bool all with passed axis=1: [False False False] Reduce bool any without passed axis parameter: True Reduce bool any with passed axis=1: [ True True True]Pierwszym parametrem operatorów redukcji jest tensor, który chcemy zredukować. Drugim parametrem są indeksy wymiarów wzdłuż których chcemy przeprowadzić redukcję. Ten parametr jest opcjonalny i jeśli nie zostanie podany, redukcja zostanie wykonana na wszystkich wymiarach.
Możemy przyjrzeć się operacji reduction_sum. Przekazujemy dwuwymiarowy tensor i chcemy go skrócić wzdłuż wymiaru 1.
W naszym przypadku otrzymana suma byłaby:
[1 + 2 + 3 = 6, 4 + 5 + 6 = 15, 7 + 8 + 9 = 24]Gdybyśmy przekazali wymiar 0, wynik byłby następujący:
[1 + 4 + 7 = 12, 2 + 5 + 8 = 15, 3 + 6 + 9 = 18]Jeśli nie miniemy żadnej osi, wynik jest tylko ogólną sumą:
1 + 4 + 7 = 12, 2 + 5 + 8 = 15, 3 + 6 + 9 = 45Wszystkie funkcje redukcji mają podobny interfejs i są wymienione w dokumentacji redukcji TensorFlow.
Segmentacja
Segmentacja to proces, w którym jednym z wymiarów jest proces mapowania wymiarów na podane indeksy segmentu, a wynikowe elementy są określane przez wiersz indeksu.
Segmentacja polega w rzeczywistości na grupowaniu elementów pod powtarzającymi się indeksami, więc na przykład w naszym przypadku mamy segmentowane identyfikatory [0, 0, 1, 2, 2] stosowane na tensor tens1 , co oznacza, że pierwsza i druga tablica zostaną przekształcone po segmentacji operacji (w naszym przypadku sumowanie) i otrzyma nową tablicę, która wygląda tak (2, 8, 1, 0) = (2+0, 5+3, 3-2, -5+5) . Trzeci element w tensor tens1 pozostaje niezmieniony, ponieważ nie jest zgrupowany w żadnym powtarzalnym indeksie, a dwie ostatnie tablice są sumowane w taki sam sposób, jak w przypadku pierwszej grupy. Oprócz sumowania, TensorFlow obsługuje iloczyn, średnią, maks. i min.
import tensorflow as tf import numpy as np def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) seg_ids = tf.constant([0, 0, 1, 2, 2]) tens1 = convert(np.array([(2, 5, 3, -5), (0, 3, -2, 5), (4, 3, 5, 3), (6, 1, 4, 0), (6, 1, 4, 0)]), tf.int32) tens2 = convert(np.array([1, 2, 3, 4, 5]), tf.int32) seg_sum = tf.segment_sum(tens1, seg_ids) seg_sum_1 = tf.segment_sum(tens2, seg_ids) with tf.Session() as session: print "Segmentation sum tens1: ", session.run(seg_sum) print "Segmentation sum tens2: ", session.run(seg_sum_1) Segmentation sum tens1: [[ 2 8 1 0] [ 4 3 5 3] [12 2 8 0]] Segmentation sum tens2: [3 3 9]Narzędzia sekwencyjne
Narzędzia sekwencyjne obejmują takie metody, jak:
- funkcja argmin, która zwraca indeks o wartości min na osiach tensora wejściowego,
- funkcja argmax, która zwraca indeks o maksymalnej wartości na osiach tensora wejściowego,
- setdiff, który oblicza różnicę między dwiema listami liczb lub ciągów,
- gdzie funkcja, która zwróci elementy z dwóch przekazanych elementów x lub y, w zależności od przekazanego warunku, lub
- unikalna funkcja, która zwróci unikalne elementy w tensorze 1-D.
Poniżej przedstawiamy kilka przykładów wykonania:
import numpy as np import tensorflow as tf def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) x = convert(np.array([ [2, 2, 1, 3], [4, 5, 6, -1], [0, 1, 1, -2], [6, 2, 3, 0] ])) y = convert(np.array([1, 2, 5, 3, 7])) z = convert(np.array([1, 0, 4, 6, 2])) arg_min = tf.argmin(x, 1) arg_max = tf.argmax(x, 1) unique = tf.unique(y) diff = tf.setdiff1d(y, z) with tf.Session() as session: print "Argmin = ", session.run(arg_min) print "Argmax = ", session.run(arg_max) print "Unique_values = ", session.run(unique)[0] print "Unique_idx = ", session.run(unique)[1] print "Setdiff_values = ", session.run(diff)[0] print "Setdiff_idx = ", session.run(diff)[1] print session.run(diff)[1]Wyjście:
Argmin = [2 3 3 3] Argmax = [3 2 1 0] Unique_values = [ 1. 2. 5. 3. 7.] Unique_idx = [0 1 2 3 4] Setdiff_values = [ 5. 3. 7.] Setdiff_idx = [2 3 4]Uczenie maszynowe z TensorFlow
W tej sekcji przedstawimy przypadek użycia uczenia maszynowego z TensorFlow. Pierwszym przykładem będzie algorytm klasyfikacji danych metodą kNN, a drugi algorytm regresji liniowej.
kNN
Pierwszym algorytmem jest k-Nearest Neighbors (kNN). Jest to nadzorowany algorytm uczenia się, który wykorzystuje metryki odległości, na przykład odległość euklidesową, do klasyfikowania danych względem treningu. Jest to jeden z najprostszych algorytmów, ale wciąż bardzo wydajny do klasyfikowania danych. Plusy tego algorytmu:
- Zapewnia wysoką dokładność, gdy model treningowy jest wystarczająco duży, oraz
- Zwykle nie jest wrażliwy na wartości odstające i nie musimy mieć żadnych założeń dotyczących danych.
Wady tego algorytmu:
- Kosztowne obliczeniowo i
- Wymaga dużej ilości pamięci, w której nowe sklasyfikowane dane muszą zostać dodane do wszystkich początkowych instancji szkoleniowych.
Odległość, której użyjemy w tym przykładzie kodu, to euklidesowa, która definiuje odległość między dwoma punktami w następujący sposób:
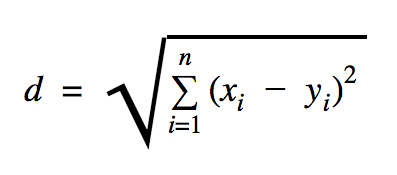
W tym wzorze n to liczba wymiarów przestrzeni, x to wektor danych uczących, a y to nowy punkt danych, który chcemy sklasyfikować.
import os import numpy as np import tensorflow as tf ccf_train_data = "train_dataset.csv" ccf_test_data = "test_dataset.csv" dataset_dir = os.path.abspath(os.path.join(os.path.dirname(__file__), '../datasets')) ccf_train_filepath = os.path.join(dataset_dir, ccf_train_data) ccf_test_filepath = os.path.join(dataset_dir, ccf_test_data) def load_data(filepath): from numpy import genfromtxt csv_data = genfromtxt(filepath, delimiter=",", skip_header=1) data = [] labels = [] for d in csv_data: data.append(d[:-1]) labels.append(d[-1]) return np.array(data), np.array(labels) train_dataset, train_labels = load_data(ccf_train_filepath) test_dataset, test_labels = load_data(ccf_test_filepath) train_pl = tf.placeholder("float", [None, 28]) test_pl = tf.placeholder("float", [28]) knn_prediction = tf.reduce_sum(tf.abs(tf.add(train_pl, tf.negative(test_pl))), axis=1) pred = tf.argmin(knn_prediction, 0) with tf.Session() as tf_session: missed = 0 for i in xrange(len(test_dataset)): knn_index = tf_session.run(pred, feed_dict={train_pl: train_dataset, test_pl: test_dataset[i]}) print "Predicted class {} -- True class {}".format(train_labels[knn_index], test_labels[i]) if train_labels[knn_index] != test_labels[i]: missed += 1 tf.summary.FileWriter("../samples/article/logs", tf_session.graph) print "Missed: {} -- Total: {}".format(missed, len(test_dataset))Zestaw danych, którego użyliśmy w powyższym przykładzie, to taki, który można znaleźć w sekcji zestawów danych Kaggle. Wykorzystaliśmy ten, który zawiera transakcje dokonywane kartami kredytowymi europejskich posiadaczy kart. Używamy danych bez żadnego czyszczenia lub filtrowania i zgodnie z opisem w Kaggle dla tego zestawu danych, są one wysoce niezrównoważone. Zestaw danych zawiera 31 zmiennych: Czas, V1, …, V28, Kwota i Klasa. W tym przykładzie kodu używamy tylko V1, …, V28 i Class. Klasa oznacza transakcje, które są fałszywe z 1 i te, które nie mają 0.
Przykładowy kod zawiera głównie rzeczy, które opisaliśmy w poprzednich rozdziałach, z wyjątkiem tego, w którym wprowadziliśmy funkcję ładowania zestawu danych. Funkcja load_data(filepath) przyjmie plik CSV jako argument i zwróci krotkę z danymi i etykietami zdefiniowanymi w CSV.
Tuż pod tą funkcją zdefiniowaliśmy placeholdery dla danych testowych i trenowanych. Przeszkolone dane są używane w modelu predykcyjnym do rozwiązywania etykiet danych wejściowych, które należy sklasyfikować. W naszym przypadku kNN używa odległości euklidesowej, aby uzyskać najbliższą etykietę.
Poziom błędu można obliczyć przez proste dzielenie przez liczbę, gdy klasyfikator pominięty przez całkowitą liczbę przykładów, która w naszym przypadku dla tego zbioru danych wynosi 0,2 (tj. klasyfikator podaje nam błędną etykietę danych dla 20% danych testowych).
Regresja liniowa
Algorytm regresji liniowej szuka liniowej zależności między dwiema zmiennymi. Jeśli oznaczymy zmienną zależną jako y, a zmienną niezależną jako x, to próbujemy oszacować parametry funkcji y = Wx + b .
Regresja liniowa jest szeroko stosowanym algorytmem w dziedzinie nauk stosowanych. Algorytm ten pozwala dodać w implementacji dwie ważne koncepcje uczenia maszynowego: funkcję kosztu oraz metodę zejścia gradientu do znajdowania minimum funkcji.
Algorytm uczenia maszynowego, który jest zaimplementowany przy użyciu tej metody, musi przewidywać wartości y jako funkcję x , gdzie algorytm regresji liniowej określi wartości W i b , które w rzeczywistości są nieznanymi i które są określane w trakcie procesu uczenia. Wybierana jest funkcja kosztu i zwykle stosuje się błąd średniokwadratowy, gdy opadanie gradientu jest algorytmem optymalizacyjnym używanym do znalezienia lokalnego minimum funkcji kosztu.
Metoda gradientu opadania jest tylko lokalnym minimum funkcji, ale może być użyta w poszukiwaniu globalnego minimum poprzez losowy wybór nowego punktu startowego po znalezieniu lokalnego minimum i powtarzanie tego procesu wiele razy. Jeśli liczba minimów funkcji jest ograniczona i jest bardzo duża liczba prób, to istnieje duża szansa, że w pewnym momencie zostanie wykryte globalne minimum. Więcej szczegółów na temat tej techniki zostawimy w artykule, o którym wspomnieliśmy we wstępie.
import tensorflow as tf import numpy as np test_data_size = 2000 iterations = 10000 learn_rate = 0.005 def generate_test_values(): train_x = [] train_y = [] for _ in xrange(test_data_size): x1 = np.random.rand() x2 = np.random.rand() x3 = np.random.rand() y_f = 2 * x1 + 3 * x2 + 7 * x3 + 4 train_x.append([x1, x2, x3]) train_y.append(y_f) return np.array(train_x), np.transpose([train_y]) x = tf.placeholder(tf.float32, [None, 3], name="x") W = tf.Variable(tf.zeros([3, 1]), name="W") b = tf.Variable(tf.zeros([1]), name="b") y = tf.placeholder(tf.float32, [None, 1]) model = tf.add(tf.matmul(x, W), b) cost = tf.reduce_mean(tf.square(y - model)) train = tf.train.GradientDescentOptimizer(learn_rate).minimize(cost) train_dataset, train_values = generate_test_values() init = tf.global_variables_initializer() with tf.Session() as session: session.run(init) for _ in xrange(iterations): session.run(train, feed_dict={ x: train_dataset, y: train_values }) print "cost = {}".format(session.run(cost, feed_dict={ x: train_dataset, y: train_values })) print "W = {}".format(session.run(W)) print "b = {}".format(session.run(b))Wyjście:
cost = 3.1083032809e-05 W = [[ 1.99049103] [ 2.9887135 ] [ 6.98754263]] b = [ 4.01742554] W powyższym przykładzie mamy dwie nowe zmienne, które nazwaliśmy cost i train . Za pomocą tych dwóch zmiennych zdefiniowaliśmy optymalizator, którego chcemy użyć w naszym modelu uczącym oraz funkcję, którą chcemy zminimalizować.
Na koniec parametry wyjściowe W i b powinny być identyczne jak te zdefiniowane w funkcji generate_test_values . W linii 17 zdefiniowaliśmy funkcję, której użyliśmy do wygenerowania liniowych punktów danych do trenowania, gdzie w1=2 , w2=3 , w3=7 i b=4 . Regresja liniowa z powyższego przykładu jest wielowymiarowa, w której używana jest więcej niż jedna zmienna niezależna.
Wniosek
Jak widać z tego samouczka TensorFlow, TensorFlow to potężna platforma, która sprawia, że praca z wyrażeniami matematycznymi i wielowymiarowymi tablicami jest dziecinnie prosta — co jest fundamentalnie niezbędne w uczeniu maszynowym. Usuwa również złożoność wykonywania wykresów danych i skalowania.
Z biegiem czasu TensorFlow zyskał na popularności i jest obecnie używany przez programistów do rozwiązywania problemów przy użyciu metod głębokiego uczenia się do rozpoznawania obrazów, wykrywania wideo, przetwarzania tekstu, takiego jak analiza sentymentu itp. Jak każda inna biblioteka, możesz potrzebować trochę czasu, aby się przyzwyczaić do koncepcji, na których opiera się TensorFlow. A kiedy już to zrobisz, z pomocą dokumentacji i wsparcia społeczności, przedstawianie problemów w postaci wykresów danych i rozwiązywanie ich za pomocą TensorFlow może sprawić, że uczenie maszynowe na dużą skalę stanie się mniej żmudnym procesem.
