Erste Schritte mit TensorFlow: Ein Tutorial zum maschinellen Lernen
Veröffentlicht: 2022-03-11TensorFlow ist eine von Google erstellte Open-Source-Softwarebibliothek, die zur Implementierung von Systemen für maschinelles Lernen und Deep Learning verwendet wird. Diese beiden Namen enthalten eine Reihe leistungsstarker Algorithmen, die eine gemeinsame Herausforderung haben – einem Computer zu ermöglichen, zu lernen, wie er automatisch komplexe Muster erkennt und/oder die bestmöglichen Entscheidungen trifft.
Wenn Sie an Details zu diesen Systemen interessiert sind, können Sie mehr in den Toptal-Blogbeiträgen zu maschinellem Lernen und Deep Learning erfahren.
TensorFlow ist im Kern eine Bibliothek für die Datenflussprogrammierung. Es nutzt verschiedene Optimierungstechniken, um die Berechnung mathematischer Ausdrücke einfacher und leistungsfähiger zu machen.
Einige der wichtigsten Funktionen von TensorFlow sind:
- Arbeitet effizient mit mathematischen Ausdrücken, die mehrdimensionale Arrays beinhalten
- Gute Unterstützung von tiefen neuronalen Netzen und maschinellen Lernkonzepten
- GPU/CPU-Computing, bei dem derselbe Code auf beiden Architekturen ausgeführt werden kann
- Hohe Skalierbarkeit der Berechnung über Maschinen und riesige Datensätze hinweg
Zusammen machen diese Funktionen TensorFlow zum perfekten Framework für Maschinenintelligenz im Produktionsmaßstab.
In diesem TensorFlow-Tutorial erfahren Sie, wie Sie einfache, aber leistungsstarke maschinelle Lernmethoden in TensorFlow verwenden und einige seiner Hilfsbibliotheken verwenden können, um die damit erstellten Modelle zu debuggen, zu visualisieren und zu optimieren.
TensorFlow installieren
Wir verwenden die TensorFlow-Python-API, die mit Python 2.7 und Python 3.3+ funktioniert. Die GPU-Version (nur Linux) erfordert das Cuda Toolkit 7.0+ und cuDNN v2+.
Wir werden das Conda-Paketabhängigkeitsverwaltungssystem verwenden, um TensorFlow zu installieren. Mit Conda können wir mehrere Umgebungen auf einer Maschine trennen. Hier erfahren Sie, wie Sie Conda installieren.
Nach der Installation von Conda können wir die Umgebung erstellen, die wir für die Installation und Verwendung von TensorFlow verwenden werden. Der folgende Befehl erstellt unsere Umgebung mit einigen zusätzlichen Bibliotheken wie NumPy, was sehr nützlich ist, sobald wir anfangen, TensorFlow zu verwenden.
Die in dieser Umgebung installierte Python-Version ist 2.7, und wir werden diese Version in diesem Artikel verwenden.
conda create --name TensorflowEnv biopython Der Einfachheit halber installieren wir hier Biopython statt nur NumPy. Dazu gehören NumPy und einige andere Pakete, die wir benötigen werden. Sie können die Pakete jederzeit nach Bedarf mit den conda install oder pip install .
Der folgende Befehl aktiviert die erstellte Conda-Umgebung. Wir können darin installierte Pakete verwenden, ohne sie mit Paketen zu vermischen, die global oder in einigen anderen Umgebungen installiert sind.
source activate TensorFlowEnvDas Pip-Installationstool ist ein Standardbestandteil einer Conda-Umgebung. Wir werden es verwenden, um die TensorFlow-Bibliothek zu installieren. Davor ist es ein guter erster Schritt, pip mit dem folgenden Befehl auf die neueste Version zu aktualisieren:
pip install --upgrade pipJetzt können wir TensorFlow installieren, indem wir Folgendes ausführen:
pip install tensorflowDas Herunterladen und Erstellen von TensorFlow kann mehrere Minuten dauern. Zum Zeitpunkt des Schreibens wird TensorFlow 1.1.0 installiert.
Datenflussdiagramme
In TensorFlow wird die Berechnung mithilfe von Datenflussdiagrammen beschrieben. Jeder Knoten des Graphen repräsentiert eine Instanz einer mathematischen Operation (wie Addition, Division oder Multiplikation) und jede Kante ist ein mehrdimensionaler Datensatz (Tensor), an dem die Operationen durchgeführt werden.
Da TensorFlow mit Berechnungsgraphen arbeitet, werden diese so verwaltet, dass jeder Knoten die Instanziierung einer Operation darstellt, wobei jede Operation null oder mehr Eingaben und null oder mehr Ausgaben hat.
Kanten in TensorFlow können in zwei Kategorien eingeteilt werden: Normale Kanten übertragen Datenstrukturen (Tensoren), bei denen es möglich ist, dass die Ausgabe einer Operation zur Eingabe für eine andere Operation wird, und spezielle Kanten, die verwendet werden, um die Abhängigkeit zwischen zwei Knoten zu steuern Betriebsreihenfolge, bei der ein Knoten auf die Beendigung eines anderen wartet.
Einfache Ausdrücke
Bevor wir mit der Erörterung von Elementen von TensorFlow fortfahren, werden wir zunächst eine Sitzung zum Arbeiten mit TensorFlow durchführen, um ein Gefühl dafür zu bekommen, wie ein TensorFlow-Programm aussieht.
Beginnen wir mit einfachen Ausdrücken und nehmen an, dass wir aus irgendeinem Grund die Funktion y = 5*x + 13 in TensorFlow-Manier auswerten möchten.
In einfachem Python-Code würde es so aussehen:
x = -2.0 y = 5*x + 13 print ywas uns in diesem Fall ein Ergebnis von 3,0 gibt.
Jetzt werden wir den obigen Ausdruck in TensorFlow-Terme umwandeln.
Konstanten
In TensorFlow werden Konstanten mithilfe der Funktion constant erstellt, die die Signatur constant(value, dtype=None, shape=None, name='Const', verify_shape=False) hat, wobei value ein tatsächlicher konstanter Wert ist, der in verwendet wird Für die weitere Berechnung ist dtype der Datentypparameter (z. B. float32/64, int8/16 usw.), shape sind optionale Dimensionen, name ist ein optionaler Name für den Tensor und der letzte Parameter ist ein boolescher Wert, der die Überprüfung von anzeigt Gestalt der Werte.
Wenn Sie Konstanten mit bestimmten Werten in Ihrem Trainingsmodell benötigen, kann das constant wie im folgenden Beispiel verwendet werden:
z = tf.constant(5.2, name="x", dtype=tf.float32)Variablen
Variablen in TensorFlow sind In-Memory-Puffer, die Tensoren enthalten, die explizit initialisiert und im Diagramm verwendet werden müssen, um den Status über die Sitzung hinweg beizubehalten. Durch einfaches Aufrufen des Konstruktors wird die Variable im Berechnungsgraphen hinzugefügt.
Variablen sind besonders nützlich, wenn Sie mit dem Training von Modellen beginnen, und sie werden verwendet, um Parameter zu speichern und zu aktualisieren. Ein als Argument eines Konstruktors übergebener Anfangswert stellt einen Tensor oder ein Objekt dar, das konvertiert oder als Tensor zurückgegeben werden kann. Das heißt, wenn wir eine Variable mit einigen vordefinierten oder zufälligen Werten füllen möchten, die später im Trainingsprozess verwendet und über Iterationen aktualisiert werden sollen, können wir sie folgendermaßen definieren:
k = tf.Variable(tf.zeros([1]), name="k")Eine andere Möglichkeit, Variablen in TensorFlow zu verwenden, sind Berechnungen, bei denen diese Variable nicht trainierbar ist und wie folgt definiert werden kann:
k = tf.Variable(tf.add(a, b), trainable=False)Sitzungen
Um die Knoten tatsächlich auszuwerten, müssen wir innerhalb einer Sitzung einen Berechnungsgraphen ausführen.
Eine Sitzung kapselt die Steuerung und den Zustand der TensorFlow-Laufzeit. Eine Sitzung ohne Parameter verwendet das in der aktuellen Sitzung erstellte Standarddiagramm, andernfalls akzeptiert die Sitzungsklasse einen Diagrammparameter, der in dieser auszuführenden Sitzung verwendet wird.
Nachfolgend finden Sie ein kurzes Code-Snippet, das zeigt, wie die oben definierten Begriffe in TensorFlow verwendet werden können, um eine einfache lineare Funktion zu berechnen.
import tensorflow as tf x = tf.constant(-2.0, name="x", dtype=tf.float32) a = tf.constant(5.0, name="a", dtype=tf.float32) b = tf.constant(13.0, name="b", dtype=tf.float32) y = tf.Variable(tf.add(tf.multiply(a, x), b)) init = tf.global_variables_initializer() with tf.Session() as session: session.run(init) print session.run(y)Verwenden von TensorFlow: Definieren von Berechnungsdiagrammen
Das Gute an der Arbeit mit Datenflussdiagrammen ist, dass das Ausführungsmodell von seiner Ausführung (auf CPU, GPU oder einer Kombination) getrennt ist, wo nach der Implementierung Software in TensorFlow auf der CPU oder GPU verwendet werden kann, wo sich die gesamte Komplexität auf den Code bezieht Ausführung ist verborgen.
Das Berechnungsdiagramm kann im Prozess der Verwendung der TensorFlow-Bibliothek erstellt werden, ohne dass Graph-Objekte explizit instanziiert werden müssen.
Ein Graph-Objekt in TensorFlow kann als Ergebnis einer einfachen Codezeile wie c = tf.add(a, b) . Dadurch wird ein Operationsknoten erstellt, der zwei Tensoren a und b verwendet, die ihre Summe c als Ausgabe erzeugen.
Das Berechnungsdiagramm ist ein integrierter Prozess, der die Bibliothek verwendet, ohne das Diagrammobjekt direkt aufrufen zu müssen. Ein Diagrammobjekt in TensorFlow, das eine Reihe von Operationen und Tensoren als Dateneinheiten enthält, wird zwischen Operationen verwendet, die denselben Prozess ermöglichen und mehr als ein Diagramm enthalten, wobei jedes Diagramm einer anderen Sitzung zugewiesen wird. Beispielsweise erstellt die einfache Codezeile c = tf.add(a, b) einen Operationsknoten, der zwei Tensoren a und b als Eingabe nimmt und ihre Summe c als Ausgabe erzeugt.
TensorFlow bietet auch einen Feed-Mechanismus zum Patchen eines Tensors zu einer beliebigen Operation im Diagramm, wobei der Feed die Ausgabe einer Operation durch den Tensorwert ersetzt. Die Feed-Daten werden als Argument beim Aufruf der Funktion run() übergeben.
Ein Platzhalter ist die Methode von TensorFlow, Entwicklern das Einfügen von Daten in das Berechnungsdiagramm durch Platzhalter zu ermöglichen, die in einige Ausdrücke eingebunden sind. Die Signatur des Platzhalters lautet:
placeholder(dtype, shape=None, name=None)wobei dtype der Typ der Elemente in den Tensoren ist und sowohl die Form der zu fütternden Tensoren als auch den Namen für die Operation liefern kann.
Wenn die Form nicht übergeben wird, kann dieser Tensor mit einer beliebigen Form gefüttert werden. Ein wichtiger Hinweis ist, dass der Platzhalter-Tensor mit Daten gefüttert werden muss, da sonst beim Ausführen der Sitzung und wenn dieser Teil fehlt, der Platzhalter einen Fehler mit der folgenden Struktur generiert:
InvalidArgumentError (see above for traceback): You must feed a value for placeholder tensor 'y' with dtype floatDer Vorteil von Platzhaltern besteht darin, dass sie es Entwicklern ermöglichen, Operationen und den Berechnungsgraphen im Allgemeinen zu erstellen, ohne die Daten dafür im Voraus bereitstellen zu müssen, und die Daten zur Laufzeit aus externen Quellen hinzugefügt werden können.
Nehmen wir ein einfaches Problem der Multiplikation zweier ganzer Zahlen x und y in TensorFlow-Manier, bei dem ein Platzhalter zusammen mit einem Feed-Mechanismus durch die Session- run -Methode verwendet wird.
import tensorflow as tf x = tf.placeholder(tf.float32, name="x") y = tf.placeholder(tf.float32, name="y") z = tf.multiply(x, y, name="z") with tf.Session() as session: print session.run(z, feed_dict={x: 2.1, y: 3.0})Visualisierung des Computational Graph mit TensorBoard
TensorBoard ist ein Visualisierungstool zur Analyse von Datenflussdiagrammen. Dies kann nützlich sein, um Modelle für maschinelles Lernen besser zu verstehen.
Mit TensorBoard können Sie Einblick in verschiedene Arten von Statistiken über die Parameter und Details über die Teile des Berechnungsdiagramms im Allgemeinen gewinnen. Es ist nicht ungewöhnlich, dass ein tiefes neuronales Netzwerk eine große Anzahl von Knoten hat. TensorBoard ermöglicht Entwicklern einen Einblick in jeden Knoten und wie die Berechnung über die TensorFlow-Laufzeit ausgeführt wird.
Kommen wir nun zurück zu unserem Beispiel vom Anfang dieses TensorFlow-Tutorials, in dem wir eine lineare Funktion mit dem Format y = a*x + b definiert haben.
Um Ereignisse aus Sitzungen zu protokollieren, die später in TensorBoard verwendet werden können, stellt TensorFlow die FileWriter -Klasse bereit. Es kann verwendet werden, um eine Ereignisdatei zum Speichern von Zusammenfassungen zu erstellen, wobei der Konstruktor sechs Parameter akzeptiert und wie folgt aussieht:
__init__(logdir, graph=None, max_queue=10, flush_secs=120, graph_def=None, filename_suffix=None)wobei der logdir-Parameter erforderlich ist und andere Standardwerte haben. Der Diagrammparameter wird aus dem im Trainingsprogramm erstellten Sitzungsobjekt übergeben. Der vollständige Beispielcode sieht folgendermaßen aus:
import tensorflow as tf x = tf.constant(-2.0, name="x", dtype=tf.float32) a = tf.constant(5.0, name="a", dtype=tf.float32) b = tf.constant(13.0, name="b", dtype=tf.float32) y = tf.Variable(tf.add(tf.multiply(a, x), b)) init = tf.global_variables_initializer() with tf.Session() as session: merged = tf.summary.merge_all() // new writer = tf.summary.FileWriter("logs", session.graph) // new session.run(init) print session.run(y) Wir haben nur zwei neue Zeilen hinzugefügt. Wir führen alle im Standarddiagramm gesammelten Zusammenfassungen zusammen, und FileWriter wird verwendet, um Ereignisse wie oben beschrieben in die Datei auszugeben.
Nach dem Ausführen des Programms haben wir die Datei in den Verzeichnisprotokollen, und der letzte Schritt besteht darin, tensorboard :
tensorboard --logdir logs/ Jetzt wird TensorBoard gestartet und läuft auf dem Standardport 6006. Nachdem Sie http://localhost:6006 geöffnet und auf das Menüelement Graphs (oben auf der Seite) geklickt haben, können Sie das Diagramm wie das hier sehen im Bild unten:
TensorBoard markiert Konstanten und Zusammenfassungsknoten mit spezifischen Symbolen, die im Folgenden beschrieben werden.
Mathematik mit TensorFlow
Tensoren sind die grundlegenden Datenstrukturen in TensorFlow und stellen die Verbindungskanten in einem Datenflussdiagramm dar.
Ein Tensor identifiziert einfach ein mehrdimensionales Array oder eine Liste. Die Tensorstruktur kann mit drei Parametern identifiziert werden: Rang, Form und Typ.
- Rang: Identifiziert die Anzahl der Dimensionen des Tensors. Ein Rang ist als Ordnung oder n-Dimension eines Tensors bekannt, wobei beispielsweise der Tensor Rang 1 ein Vektor oder der Tensor Rang 2 eine Matrix ist.
- Form: Die Form eines Tensors ist die Anzahl der Zeilen und Spalten, die er hat.
- Typ: Der den Tensorelementen zugewiesene Datentyp.
Um einen Tensor in TensorFlow zu erstellen, können wir ein n-dimensionales Array erstellen. Dies kann einfach mit der NumPy-Bibliothek oder durch Konvertieren eines n-dimensionalen Python-Arrays in einen TensorFlow-Tensor erfolgen.
Um einen 1-D-Tensor zu erstellen, verwenden wir ein NumPy-Array, das wir erstellen, indem wir eine integrierte Python-Liste übergeben.
import numpy as np tensor_1d = np.array([1.45, -1, 0.2, 102.1])Das Arbeiten mit dieser Art von Array ähnelt dem Arbeiten mit einer integrierten Python-Liste. Der Hauptunterschied besteht darin, dass das NumPy-Array auch einige zusätzliche Eigenschaften wie Dimension, Form und Typ enthält.
> > print tensor1d [ 1.45 -1. 0.2 102.1 ] > > print tensor1d[0] 1.45 > > print tensor1d[2] 0.2 > > print tensor1d.ndim 1 > > print tensor1d.shape (4,) > > print tensor1d.dtype float64Ein NumPy-Array lässt sich einfach mit der Hilfsfunktion convert_to_tensor in einen TensorFlow-Tensor umwandeln, die Entwicklern hilft, Python-Objekte in Tensor-Objekte umzuwandeln. Diese Funktion akzeptiert Tensorobjekte, NumPy-Arrays, Python-Listen und Python-Skalare.
tensor = tf.convert_to_tensor(tensor_1d, dtype=tf.float64)Wenn wir nun unseren Tensor an die TensorFlow-Sitzung binden, können wir die Ergebnisse unserer Konvertierung sehen.
tensor = tf.convert_to_tensor(tensor_1d, dtype=tf.float64) with tf.Session() as session: print session.run(tensor) print session.run(tensor[0]) print session.run(tensor[1])Ausgabe:
[ 1.45 -1. 0.2 102.1 ] 1.45 -1.0Wir können auf ähnliche Weise einen 2-D-Tensor oder eine Matrix erstellen:
tensor_2d = np.array(np.random.rand(4, 4), dtype='float32') tensor_2d_1 = np.array(np.random.rand(4, 4), dtype='float32') tensor_2d_2 = np.array(np.random.rand(4, 4), dtype='float32') m1 = tf.convert_to_tensor(tensor_2d) m2 = tf.convert_to_tensor(tensor_2d_1) m3 = tf.convert_to_tensor(tensor_2d_2) mat_product = tf.matmul(m1, m2) mat_sum = tf.add(m2, m3) mat_det = tf.matrix_determinant(m3) with tf.Session() as session: print session.run(mat_product) print session.run(mat_sum) print session.run(mat_det)Tensoroperationen
Im obigen Beispiel führen wir einige TensorFlow-Operationen an den Vektoren und Matrizen ein. Die Operationen führen bestimmte Berechnungen an den Tensoren durch. Welche Berechnungen das sind, zeigt die folgende Tabelle.
| TensorFlow-Operator | Beschreibung |
|---|---|
| tf.add | x+y |
| tf.subtrahieren | xy |
| tf.multiplizieren | x*y |
| tf.div | x/y |
| tf.mod | x % y |
| tf.abs | |x| |
| tf.negativ | -x |
| tf.sign | Zeichen (x) |
| tf.Quadrat | x*x |
| tf.rund | Runde (x) |
| tf.sqrt | quadrat(x) |
| tf.pow | x^y |
| tf.exp | z. B |
| tf.log | log(x) |
| tf.maximum | max(x,y) |
| tf.minimum | min(x, y) |
| tf.cos | cos(x) |
| tf.sin | Sünde (x) |
Die in der obigen Tabelle aufgeführten TensorFlow-Operationen arbeiten mit Tensorobjekten und werden elementweise ausgeführt. Wenn Sie also den Kosinus für einen Vektor x berechnen möchten, führt die TensorFlow-Operation Berechnungen für jedes Element im übergebenen Tensor durch.

tensor_1d = np.array([0, 0, 0]) tensor = tf.convert_to_tensor(tensor_1d, dtype=tf.float64) with tf.Session() as session: print session.run(tf.cos(tensor))Ausgabe:
[ 1. 1. 1.]Matrixoperationen
Matrixoperationen sind sehr wichtig für maschinelle Lernmodelle, wie die lineare Regression, da sie dort häufig verwendet werden. TensorFlow unterstützt alle gängigen Matrizenoperationen wie Multiplikation, Transponierung, Inversion, Berechnung der Determinante, Lösung linearer Gleichungen und vieles mehr.
Als nächstes werden wir einige der Matrixoperationen erklären. Sie sind in der Regel wichtig, wenn es um maschinelle Lernmodelle geht, z. B. bei der linearen Regression. Lassen Sie uns einen Code schreiben, der grundlegende Matrizenoperationen wie Multiplikation, Ermitteln der Transponierung, Ermitteln der Determinante, Multiplikation, Sol und vieles mehr ausführt.
Nachfolgend finden Sie grundlegende Beispiele für den Aufruf dieser Operationen.
import tensorflow as tf import numpy as np def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) m1 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m2 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m3 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m4 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m5 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m_tranpose = tf.transpose(m1) m_mul = tf.matmul(m1, m2) m_det = tf.matrix_determinant(m3) m_inv = tf.matrix_inverse(m4) m_solve = tf.matrix_solve(m5, [[1], [1], [1], [1]]) with tf.Session() as session: print session.run(m_tranpose) print session.run(m_mul) print session.run(m_inv) print session.run(m_det) print session.run(m_solve)Daten transformieren
Die Ermäßigung
TensorFlow unterstützt verschiedene Arten der Reduktion. Reduktion ist eine Operation, die eine oder mehrere Dimensionen aus einem Tensor entfernt, indem bestimmte Operationen über diese Dimensionen hinweg durchgeführt werden. Eine Liste der unterstützten Reduzierungen für die aktuelle Version von TensorFlow finden Sie hier. Einige davon stellen wir Ihnen im folgenden Beispiel vor.
import tensorflow as tf import numpy as np def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) x = convert( np.array( [ (1, 2, 3), (4, 5, 6), (7, 8, 9) ]), tf.int32) bool_tensor = convert([(True, False, True), (False, False, True), (True, False, False)], tf.bool) red_sum_0 = tf.reduce_sum(x) red_sum = tf.reduce_sum(x, axis=1) red_prod_0 = tf.reduce_prod(x) red_prod = tf.reduce_prod(x, axis=1) red_min_0 = tf.reduce_min(x) red_min = tf.reduce_min(x, axis=1) red_max_0 = tf.reduce_max(x) red_max = tf.reduce_max(x, axis=1) red_mean_0 = tf.reduce_mean(x) red_mean = tf.reduce_mean(x, axis=1) red_bool_all_0 = tf.reduce_all(bool_tensor) red_bool_all = tf.reduce_all(bool_tensor, axis=1) red_bool_any_0 = tf.reduce_any(bool_tensor) red_bool_any = tf.reduce_any(bool_tensor, axis=1) with tf.Session() as session: print "Reduce sum without passed axis parameter: ", session.run(red_sum_0) print "Reduce sum with passed axis=1: ", session.run(red_sum) print "Reduce product without passed axis parameter: ", session.run(red_prod_0) print "Reduce product with passed axis=1: ", session.run(red_prod) print "Reduce min without passed axis parameter: ", session.run(red_min_0) print "Reduce min with passed axis=1: ", session.run(red_min) print "Reduce max without passed axis parameter: ", session.run(red_max_0) print "Reduce max with passed axis=1: ", session.run(red_max) print "Reduce mean without passed axis parameter: ", session.run(red_mean_0) print "Reduce mean with passed axis=1: ", session.run(red_mean) print "Reduce bool all without passed axis parameter: ", session.run(red_bool_all_0) print "Reduce bool all with passed axis=1: ", session.run(red_bool_all) print "Reduce bool any without passed axis parameter: ", session.run(red_bool_any_0) print "Reduce bool any with passed axis=1: ", session.run(red_bool_any)Ausgabe:
Reduce sum without passed axis parameter: 45 Reduce sum with passed axis=1: [ 6 15 24] Reduce product without passed axis parameter: 362880 Reduce product with passed axis=1: [ 6 120 504] Reduce min without passed axis parameter: 1 Reduce min with passed axis=1: [1 4 7] Reduce max without passed axis parameter: 9 Reduce max with passed axis=1: [3 6 9] Reduce mean without passed axis parameter: 5 Reduce mean with passed axis=1: [2 5 8] Reduce bool all without passed axis parameter: False Reduce bool all with passed axis=1: [False False False] Reduce bool any without passed axis parameter: True Reduce bool any with passed axis=1: [ True True True]Der erste Parameter von Reduktionsoperatoren ist der Tensor, den wir reduzieren wollen. Der zweite Parameter sind die Indizes der Dimensionen, entlang denen wir die Reduktion durchführen wollen. Dieser Parameter ist optional, und wenn er nicht übergeben wird, wird die Reduktion entlang aller Dimensionen durchgeführt.
Wir können uns die Operation Reduce_sum ansehen. Wir übergeben einen 2-D-Tensor und wollen ihn entlang der Dimension 1 reduzieren.
In unserem Fall wäre die resultierende Summe:
[1 + 2 + 3 = 6, 4 + 5 + 6 = 15, 7 + 8 + 9 = 24]Wenn wir die Dimension 0 übergeben, wäre das Ergebnis:
[1 + 4 + 7 = 12, 2 + 5 + 8 = 15, 3 + 6 + 9 = 18]Wenn wir keine Achse passieren, ist das Ergebnis nur die Gesamtsumme von:
1 + 4 + 7 = 12, 2 + 5 + 8 = 15, 3 + 6 + 9 = 45Alle Reduktionsfunktionen haben eine ähnliche Schnittstelle und sind in der TensorFlow-Reduktionsdokumentation aufgeführt.
Segmentierung
Die Segmentierung ist ein Prozess, bei dem eine der Dimensionen der Prozess der Abbildung von Dimensionen auf bereitgestellte Segmentindizes ist und die resultierenden Elemente durch eine Indexzeile bestimmt werden.
Bei der Segmentierung werden die Elemente tatsächlich unter wiederholten Indizes gruppiert. In unserem Fall haben wir beispielsweise segmentierte IDs [0, 0, 1, 2, 2] auf den Tensor tens1 angewendet, was bedeutet, dass das erste und das zweite Array nach der Segmentierung transformiert werden Operation (in unserem Fall Summation) und erhält ein neues Array, das wie folgt aussieht (2, 8, 1, 0) = (2+0, 5+3, 3-2, -5+5) . Das dritte Element in Tensor tens1 bleibt unberührt, da es in keinem wiederholten Index gruppiert ist und die letzten beiden Arrays auf die gleiche Weise summiert werden wie bei der ersten Gruppe. Neben der Summierung unterstützt TensorFlow Produkt, Mittelwert, Max und Min.
import tensorflow as tf import numpy as np def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) seg_ids = tf.constant([0, 0, 1, 2, 2]) tens1 = convert(np.array([(2, 5, 3, -5), (0, 3, -2, 5), (4, 3, 5, 3), (6, 1, 4, 0), (6, 1, 4, 0)]), tf.int32) tens2 = convert(np.array([1, 2, 3, 4, 5]), tf.int32) seg_sum = tf.segment_sum(tens1, seg_ids) seg_sum_1 = tf.segment_sum(tens2, seg_ids) with tf.Session() as session: print "Segmentation sum tens1: ", session.run(seg_sum) print "Segmentation sum tens2: ", session.run(seg_sum_1) Segmentation sum tens1: [[ 2 8 1 0] [ 4 3 5 3] [12 2 8 0]] Segmentation sum tens2: [3 3 9]Sequenz-Dienstprogramme
Zu den Sequenzdienstprogrammen gehören Methoden wie:
- argmin-Funktion, die den Index mit dem Mindestwert über die Achsen des Eingabetensors zurückgibt,
- argmax-Funktion, die den Index mit dem maximalen Wert über die Achsen des Eingabetensors zurückgibt,
- setdiff, das die Differenz zwischen zwei Listen von Zahlen oder Strings berechnet,
- where-Funktion, die Elemente entweder von zwei übergebenen Elementen x oder y zurückgibt, was von der übergebenen Bedingung abhängt, oder
- Unique-Funktion, die eindeutige Elemente in einem 1-D-Tensor zurückgibt.
Nachfolgend zeigen wir einige Ausführungsbeispiele:
import numpy as np import tensorflow as tf def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) x = convert(np.array([ [2, 2, 1, 3], [4, 5, 6, -1], [0, 1, 1, -2], [6, 2, 3, 0] ])) y = convert(np.array([1, 2, 5, 3, 7])) z = convert(np.array([1, 0, 4, 6, 2])) arg_min = tf.argmin(x, 1) arg_max = tf.argmax(x, 1) unique = tf.unique(y) diff = tf.setdiff1d(y, z) with tf.Session() as session: print "Argmin = ", session.run(arg_min) print "Argmax = ", session.run(arg_max) print "Unique_values = ", session.run(unique)[0] print "Unique_idx = ", session.run(unique)[1] print "Setdiff_values = ", session.run(diff)[0] print "Setdiff_idx = ", session.run(diff)[1] print session.run(diff)[1]Ausgabe:
Argmin = [2 3 3 3] Argmax = [3 2 1 0] Unique_values = [ 1. 2. 5. 3. 7.] Unique_idx = [0 1 2 3 4] Setdiff_values = [ 5. 3. 7.] Setdiff_idx = [2 3 4]Maschinelles Lernen mit TensorFlow
In diesem Abschnitt stellen wir einen Anwendungsfall für maschinelles Lernen mit TensorFlow vor. Das erste Beispiel wird ein Algorithmus zur Klassifizierung von Daten mit dem kNN-Ansatz sein, und das zweite wird den linearen Regressionsalgorithmus verwenden.
kNN
Der erste Algorithmus ist k-Nearest Neighbors (kNN). Es handelt sich um einen überwachten Lernalgorithmus, der Entfernungsmetriken verwendet, beispielsweise die euklidische Entfernung, um Daten anhand des Trainings zu klassifizieren. Es ist einer der einfachsten Algorithmen, aber immer noch sehr leistungsfähig zum Klassifizieren von Daten. Vorteile dieses Algorithmus:
- Bietet eine hohe Genauigkeit, wenn das Trainingsmodell groß genug ist, und
- Reagiert normalerweise nicht auf Ausreißer, und wir müssen keine Annahmen über Daten haben.
Nachteile dieses Algorithmus:
- Rechnerisch teuer und
- Benötigt viel Speicher, wenn neue klassifizierte Daten zu allen anfänglichen Trainingsinstanzen hinzugefügt werden müssen.
Der Abstand, den wir in diesem Codebeispiel verwenden werden, ist euklidisch, was den Abstand zwischen zwei Punkten wie folgt definiert:
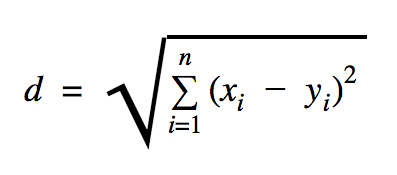
In dieser Formel ist n die Anzahl der Dimensionen des Raums, x der Vektor der Trainingsdaten und y ein neuer Datenpunkt, den wir klassifizieren möchten.
import os import numpy as np import tensorflow as tf ccf_train_data = "train_dataset.csv" ccf_test_data = "test_dataset.csv" dataset_dir = os.path.abspath(os.path.join(os.path.dirname(__file__), '../datasets')) ccf_train_filepath = os.path.join(dataset_dir, ccf_train_data) ccf_test_filepath = os.path.join(dataset_dir, ccf_test_data) def load_data(filepath): from numpy import genfromtxt csv_data = genfromtxt(filepath, delimiter=",", skip_header=1) data = [] labels = [] for d in csv_data: data.append(d[:-1]) labels.append(d[-1]) return np.array(data), np.array(labels) train_dataset, train_labels = load_data(ccf_train_filepath) test_dataset, test_labels = load_data(ccf_test_filepath) train_pl = tf.placeholder("float", [None, 28]) test_pl = tf.placeholder("float", [28]) knn_prediction = tf.reduce_sum(tf.abs(tf.add(train_pl, tf.negative(test_pl))), axis=1) pred = tf.argmin(knn_prediction, 0) with tf.Session() as tf_session: missed = 0 for i in xrange(len(test_dataset)): knn_index = tf_session.run(pred, feed_dict={train_pl: train_dataset, test_pl: test_dataset[i]}) print "Predicted class {} -- True class {}".format(train_labels[knn_index], test_labels[i]) if train_labels[knn_index] != test_labels[i]: missed += 1 tf.summary.FileWriter("../samples/article/logs", tf_session.graph) print "Missed: {} -- Total: {}".format(missed, len(test_dataset))Der Datensatz, den wir im obigen Beispiel verwendet haben, ist einer, der im Abschnitt Kaggle-Datensätze zu finden ist. Wir haben diejenige verwendet, die Transaktionen enthält, die mit Kreditkarten europäischer Karteninhaber getätigt wurden. Wir verwenden die Daten ohne jegliche Bereinigung oder Filterung und gemäß der Beschreibung in Kaggle für diesen Datensatz ist er sehr unausgeglichen. Der Datensatz enthält 31 Variablen: Zeit, V1, …, V28, Betrag und Klasse. In diesem Codebeispiel verwenden wir nur V1, …, V28 und Class. Die Klasse kennzeichnet Transaktionen, die betrügerisch sind, mit 1 und solche, die keine sind, mit 0.
Das Codebeispiel enthält hauptsächlich die Dinge, die wir in den vorherigen Abschnitten beschrieben haben, mit der Ausnahme, wo wir die Funktion zum Laden eines Datensatzes eingeführt haben. Die Funktion load_data(filepath) nimmt eine CSV-Datei als Argument und gibt ein Tupel mit in CSV definierten Daten und Labels zurück.
Direkt unterhalb dieser Funktion haben wir Platzhalter für die Test- und Trainingsdaten definiert. Trainierte Daten werden im Vorhersagemodell verwendet, um die Labels für die zu klassifizierenden Eingabedaten aufzulösen. In unserem Fall verwendet kNN die euklidische Distanz, um das nächstgelegene Etikett zu erhalten.
Die Fehlerquote kann durch einfache Division mit der Zahl berechnet werden, wenn ein Klassifikator die Gesamtzahl der Beispiele verfehlt hat, was in unserem Fall für diesen Datensatz 0,2 ist (dh der Klassifikator gibt uns für 20 % der Testdaten das falsche Datenetikett).
Lineare Regression
Der lineare Regressionsalgorithmus sucht nach einer linearen Beziehung zwischen zwei Variablen. Wenn wir die abhängige Variable als y und die unabhängige Variable als x bezeichnen, versuchen wir, die Parameter der Funktion y = Wx + b zu schätzen.
Die lineare Regression ist ein weit verbreiteter Algorithmus im Bereich der angewandten Wissenschaften. Dieser Algorithmus ermöglicht das Hinzufügen von zwei wichtigen Konzepten des maschinellen Lernens in der Implementierung: Kostenfunktion und die Gradientenabstiegsmethode zum Finden des Minimums der Funktion.
Ein maschineller Lernalgorithmus, der unter Verwendung dieses Verfahrens implementiert wird, muss Werte von y als eine Funktion von x vorhersagen, wobei ein linearer Regressionsalgorithmus Werte W und b bestimmen wird, die tatsächlich Unbekannte sind und die über den Trainingsprozess hinweg bestimmt werden. Eine Kostenfunktion wird gewählt, und normalerweise wird der mittlere quadratische Fehler verwendet, wobei der Gradientenabstieg der Optimierungsalgorithmus ist, der verwendet wird, um ein lokales Minimum der Kostenfunktion zu finden.
Das Gradientenabstiegsverfahren ist nur ein lokales Funktionsminimum, aber es kann bei der Suche nach einem globalen Minimum verwendet werden, indem ein neuer Startpunkt zufällig ausgewählt wird, sobald es ein lokales Minimum gefunden hat, und dieser Vorgang viele Male wiederholt wird. Wenn die Anzahl der Minima der Funktion begrenzt ist und die Anzahl der Versuche sehr hoch ist, besteht eine gute Chance, dass irgendwann das globale Minimum entdeckt wird. Einige weitere Details zu dieser Technik werden wir für den Artikel hinterlassen, den wir im Einführungsabschnitt erwähnt haben.
import tensorflow as tf import numpy as np test_data_size = 2000 iterations = 10000 learn_rate = 0.005 def generate_test_values(): train_x = [] train_y = [] for _ in xrange(test_data_size): x1 = np.random.rand() x2 = np.random.rand() x3 = np.random.rand() y_f = 2 * x1 + 3 * x2 + 7 * x3 + 4 train_x.append([x1, x2, x3]) train_y.append(y_f) return np.array(train_x), np.transpose([train_y]) x = tf.placeholder(tf.float32, [None, 3], name="x") W = tf.Variable(tf.zeros([3, 1]), name="W") b = tf.Variable(tf.zeros([1]), name="b") y = tf.placeholder(tf.float32, [None, 1]) model = tf.add(tf.matmul(x, W), b) cost = tf.reduce_mean(tf.square(y - model)) train = tf.train.GradientDescentOptimizer(learn_rate).minimize(cost) train_dataset, train_values = generate_test_values() init = tf.global_variables_initializer() with tf.Session() as session: session.run(init) for _ in xrange(iterations): session.run(train, feed_dict={ x: train_dataset, y: train_values }) print "cost = {}".format(session.run(cost, feed_dict={ x: train_dataset, y: train_values })) print "W = {}".format(session.run(W)) print "b = {}".format(session.run(b))Ausgabe:
cost = 3.1083032809e-05 W = [[ 1.99049103] [ 2.9887135 ] [ 6.98754263]] b = [ 4.01742554] Im obigen Beispiel haben wir zwei neue Variablen, die wir cost und train genannt haben. Mit diesen beiden Variablen haben wir einen Optimierer definiert, den wir in unserem Trainingsmodell verwenden möchten, und die Funktion, die wir minimieren möchten.
Am Ende sollten die Ausgabeparameter von W und b identisch sein mit denen, die in der Funktion generate_test_values definiert sind. In Zeile 17 haben wir tatsächlich eine Funktion definiert, die wir verwendet haben, um die linearen Datenpunkte zu generieren, um zu trainieren, wobei w1=2 , w2=3 , w3=7 und b=4 . Die lineare Regression aus dem obigen Beispiel ist multivariat, wobei mehr als eine unabhängige Variable verwendet wird.
Fazit
Wie Sie diesem TensorFlow-Tutorial entnehmen können, ist TensorFlow ein leistungsstarkes Framework, das die Arbeit mit mathematischen Ausdrücken und mehrdimensionalen Arrays zum Kinderspiel macht – etwas, das beim maschinellen Lernen grundlegend notwendig ist. Es abstrahiert auch die Komplexität der Ausführung der Datendiagramme und Skalierung.
Im Laufe der Zeit hat TensorFlow an Popularität gewonnen und wird jetzt von Entwicklern zur Lösung von Problemen mit Deep-Learning-Methoden für Bilderkennung, Videoerkennung, Textverarbeitung wie Stimmungsanalyse usw. verwendet. Wie bei jeder anderen Bibliothek benötigen Sie möglicherweise einige Zeit, um sich daran zu gewöhnen zu den Konzepten, auf denen TensorFlow aufbaut. Und sobald Sie dies getan haben, kann die Darstellung von Problemen als Datendiagramme und deren Lösung mit TensorFlow mithilfe von Dokumentation und Community-Unterstützung das maschinelle Lernen in großem Maßstab zu einem weniger langwierigen Prozess machen.
