Начало работы с TensorFlow: учебник по машинному обучению
Опубликовано: 2022-03-11TensorFlow — это программная библиотека с открытым исходным кодом, созданная Google, которая используется для реализации систем машинного и глубокого обучения. Эти два имени содержат серию мощных алгоритмов, которые имеют общую задачу — позволить компьютеру научиться автоматически определять сложные закономерности и/или принимать наилучшие возможные решения.
Если вас интересуют подробности об этих системах, вы можете узнать больше из сообщений блога Toptal о машинном обучении и глубоком обучении.
TensorFlow, по своей сути, представляет собой библиотеку для программирования потоков данных. Он использует различные методы оптимизации, чтобы сделать расчет математических выражений проще и эффективнее.
Некоторые из ключевых особенностей TensorFlow:
- Эффективно работает с математическими выражениями, включающими многомерные массивы.
- Хорошая поддержка глубоких нейронных сетей и концепций машинного обучения
- Вычисления на GPU/CPU, когда один и тот же код может выполняться на обеих архитектурах.
- Высокая масштабируемость вычислений между машинами и огромными наборами данных
Вместе эти функции делают TensorFlow идеальной основой для машинного интеллекта в промышленных масштабах.
В этом руководстве по TensorFlow вы узнаете, как использовать простые, но мощные методы машинного обучения в TensorFlow и как использовать некоторые из его вспомогательных библиотек для отладки, визуализации и настройки моделей, созданных с его помощью.
Установка ТензорФлоу
Мы будем использовать Python API TensorFlow, который работает с Python 2.7 и Python 3.3+. Для версии с графическим процессором (только для Linux) требуется Cuda Toolkit 7.0+ и cuDNN v2+.
Мы будем использовать систему управления зависимостями пакетов Conda для установки TensorFlow. Conda позволяет нам разделить несколько сред на машине. Вы можете узнать, как установить Conda отсюда.
После установки Conda мы можем создать среду, которую будем использовать для установки и использования TensorFlow. Следующая команда создаст нашу среду с некоторыми дополнительными библиотеками, такими как NumPy, что очень полезно, когда мы начнем использовать TensorFlow.
В этой среде установлена версия Python 2.7, и мы будем использовать эту версию в этой статье.
conda create --name TensorflowEnv biopython Чтобы упростить задачу, мы устанавливаем здесь biopython вместо NumPy. Сюда входят NumPy и несколько других пакетов, которые нам понадобятся. Вы всегда можете установить пакеты по мере необходимости, используя команды conda install или pip install .
Следующая команда активирует созданную среду Conda. Мы сможем использовать установленные в нем пакеты, не смешивая их с пакетами, установленными глобально или в некоторых других средах.
source activate TensorFlowEnvИнструмент установки pip является стандартной частью среды Conda. Мы будем использовать его для установки библиотеки TensorFlow. Перед этим хорошим первым шагом будет обновление pip до последней версии с помощью следующей команды:
pip install --upgrade pipТеперь мы готовы установить TensorFlow, запустив:
pip install tensorflowЗагрузка и сборка TensorFlow может занять несколько минут. На момент написания это устанавливает TensorFlow 1.1.0.
Графики потоков данных
В TensorFlow вычисления описываются с помощью графов потоков данных. Каждый узел графа представляет собой экземпляр математической операции (такой как сложение, деление или умножение), а каждое ребро представляет собой многомерный набор данных (тензор), над которым выполняются операции.
Поскольку TensorFlow работает с вычислительными графами, они управляются таким образом, что каждый узел представляет собой реализацию операции, где каждая операция имеет ноль или более входных данных и ноль или более выходных данных.
Ребра в TensorFlow можно разделить на две категории: обычные ребра передают структуру данных (тензоры), где возможно, что выходные данные одной операции становятся входными данными для другой операции, и специальные ребра, которые используются для управления зависимостью между двумя узлами для установки порядок работы, при котором один узел ожидает завершения другого.
Простые выражения
Прежде чем мы перейдем к обсуждению элементов TensorFlow, мы сначала проведем сеанс работы с TensorFlow, чтобы получить представление о том, как выглядит программа TensorFlow.
Давайте начнем с простых выражений и предположим, что по какой-то причине мы хотим вычислить функцию y = 5*x + 13 в стиле TensorFlow.
В простом коде Python это будет выглядеть так:
x = -2.0 y = 5*x + 13 print yчто дает нам в данном случае результат 3.0.
Теперь мы преобразуем приведенное выше выражение в термины TensorFlow.
Константы
В TensorFlow константы создаются с использованием функциональной константы, которая имеет сигнатурную constant(value, dtype=None, shape=None, name='Const', verify_shape=False) , где value — фактическое постоянное значение, которое будет использоваться в дальнейшие вычисления, dtype — это параметр типа данных (например, float32/64, int8/16 и т. д.), shape — необязательные размеры, name — необязательное имя для тензора, а последний параметр — логическое значение, указывающее на проверку форма ценностей.
Если вам нужны константы с определенными значениями внутри вашей модели обучения, то объект constant можно использовать, как в следующем примере:
z = tf.constant(5.2, name="x", dtype=tf.float32)Переменные
Переменные в TensorFlow — это буферы в памяти, содержащие тензоры, которые должны быть явно инициализированы и использованы в графе для поддержания состояния в сеансе. Просто вызывая конструктор, переменная добавляется в вычислительный граф.
Переменные особенно полезны, когда вы начинаете с моделей обучения, и они используются для хранения и обновления параметров. Начальное значение, переданное в качестве аргумента конструктора, представляет собой тензор или объект, который можно преобразовать или вернуть как тензор. Это означает, что если мы хотим заполнить переменную некоторыми предопределенными или случайными значениями, которые будут использоваться впоследствии в процессе обучения и обновляться в итерациях, мы можем определить ее следующим образом:
k = tf.Variable(tf.zeros([1]), name="k")Другой способ использования переменных в TensorFlow — в вычислениях, где эта переменная не поддается обучению и может быть определена следующим образом:
k = tf.Variable(tf.add(a, b), trainable=False)Сессии
Чтобы на самом деле оценить узлы, мы должны запустить вычислительный граф в сеансе.
Сеанс инкапсулирует управление и состояние среды выполнения TensorFlow. Сеанс без параметров будет использовать граф по умолчанию, созданный в текущем сеансе, в противном случае класс сеанса принимает параметр графа, который используется в этом сеансе для выполнения.
Ниже приведен краткий фрагмент кода, показывающий, как определенные выше термины можно использовать в TensorFlow для вычисления простой линейной функции.
import tensorflow as tf x = tf.constant(-2.0, name="x", dtype=tf.float32) a = tf.constant(5.0, name="a", dtype=tf.float32) b = tf.constant(13.0, name="b", dtype=tf.float32) y = tf.Variable(tf.add(tf.multiply(a, x), b)) init = tf.global_variables_initializer() with tf.Session() as session: session.run(init) print session.run(y)Использование TensorFlow: определение вычислительных графиков
Преимущество работы с графами потоков данных заключается в том, что модель выполнения отделена от его выполнения (на ЦП, ГП или какой-либо комбинации), где после реализации программное обеспечение в TensorFlow может использоваться на ЦП или ГП, где вся сложность связана с кодом. исполнение скрыто.
Граф вычислений можно построить в процессе использования библиотеки TensorFlow без необходимости явно создавать экземпляры объектов Graph.
Объект Graph в TensorFlow можно создать с помощью простой строки кода, например c = tf.add(a, b) . Это создаст узел операции, который принимает два тензора a и b , которые производят их сумму c в качестве вывода.
Граф вычислений — это встроенный процесс, который использует библиотеку без необходимости прямого вызова объекта графа. Объект графа в TensorFlow, который содержит набор операций и тензоров в качестве единиц данных, используется между операциями, что позволяет выполнять один и тот же процесс и содержит более одного графа, где каждый граф будет назначен другому сеансу. Например, простая строка кода c = tf.add(a, b) создаст узел операции, который принимает на вход два тензора a и b и выдает их сумму c на выходе.
TensorFlow также предоставляет механизм подачи для исправления тензора к любой операции в графе, где подача заменяет вывод операции значением тензора. Данные канала передаются в качестве аргумента при вызове функции run() .
Заполнитель — это способ TensorFlow, позволяющий разработчикам вводить данные в граф вычислений через заполнители, которые связаны внутри некоторых выражений. Подпись заполнителя:
placeholder(dtype, shape=None, name=None)где dtype — это тип элементов в тензорах, который может указывать как форму тензоров, которые нужно передать, так и имя операции.
Если форма не передана, этому тензору можно передать любую форму. Важным примечанием является то, что тензор заполнителя должен быть наполнен данными, иначе при выполнении сеанса и при отсутствии этой части заполнитель генерирует ошибку со следующей структурой:
InvalidArgumentError (see above for traceback): You must feed a value for placeholder tensor 'y' with dtype floatПреимущество плейсхолдеров в том, что они позволяют разработчикам создавать операции и вычислительный граф в целом без необходимости заранее предоставлять для этого данные, а данные могут быть добавлены во время выполнения из внешних источников.
Давайте возьмем простую задачу умножения двух целых чисел x и y в стиле TensorFlow, где заполнитель будет использоваться вместе с механизмом подачи через метод run сеанса.
import tensorflow as tf x = tf.placeholder(tf.float32, name="x") y = tf.placeholder(tf.float32, name="y") z = tf.multiply(x, y, name="z") with tf.Session() as session: print session.run(z, feed_dict={x: 2.1, y: 3.0})Визуализация вычислительного графика с помощью TensorBoard
TensorBoard — это инструмент визуализации для анализа графов потоков данных. Это может быть полезно для лучшего понимания моделей машинного обучения.
С TensorBoard вы можете получить представление о различных типах статистики о параметрах и подробностях о частях вычислительного графа в целом. Нет ничего необычного в том, что глубокая нейронная сеть имеет большое количество узлов. TensorBoard позволяет разработчикам получить представление о каждом узле и о том, как выполняются вычисления во время выполнения TensorFlow.
Теперь давайте вернемся к нашему примеру из начала этого руководства по TensorFlow, где мы определили линейную функцию в формате y = a*x + b .
Чтобы регистрировать события сеанса, которые впоследствии можно использовать в TensorBoard, TensorFlow предоставляет класс FileWriter . Его можно использовать для создания файла событий для хранения сводок, где конструктор принимает шесть параметров и выглядит так:
__init__(logdir, graph=None, max_queue=10, flush_secs=120, graph_def=None, filename_suffix=None)где параметр logdir является обязательным, а другие имеют значения по умолчанию. Параметр графика будет передан из объекта сеанса, созданного в программе обучения. Полный код примера выглядит так:
import tensorflow as tf x = tf.constant(-2.0, name="x", dtype=tf.float32) a = tf.constant(5.0, name="a", dtype=tf.float32) b = tf.constant(13.0, name="b", dtype=tf.float32) y = tf.Variable(tf.add(tf.multiply(a, x), b)) init = tf.global_variables_initializer() with tf.Session() as session: merged = tf.summary.merge_all() // new writer = tf.summary.FileWriter("logs", session.graph) // new session.run(init) print session.run(y) Мы добавили всего две новые строки. Мы объединяем все собранные сводки в график по умолчанию, а FileWriter используется для вывода событий в файл, как мы описали выше, соответственно.
После запуска программы у нас есть файл logs в каталоге, и последний шаг — запустить tensorboard :
tensorboard --logdir logs/ Теперь TensorBoard запущен и работает на порту 6006 по умолчанию. Открыв http://localhost:6006 и щелкнув пункт меню «Графики» (расположенный вверху страницы), вы сможете увидеть график, подобный тому, что на картинке ниже:
TensorBoard помечает константы и сводные узлы специальными символами, которые описаны ниже.
Математика с TensorFlow
Тензоры являются основными структурами данных в TensorFlow и представляют собой соединительные ребра в графе потока данных.
Тензор просто идентифицирует многомерный массив или список. Тензорную структуру можно идентифицировать по трем параметрам: ранг, форма и тип.
- Ранг: определяет количество измерений тензора. Ранг известен как порядок или n-мерность тензора, где, например, тензор ранга 1 представляет собой вектор, а тензор ранга 2 представляет собой матрицу.
- Форма: Форма тензора — это количество строк и столбцов, которые он имеет.
- Тип: тип данных, назначенный элементам тензора.
Чтобы построить тензор в TensorFlow, мы можем построить n-мерный массив. Это можно легко сделать с помощью библиотеки NumPy или путем преобразования n-мерного массива Python в тензор TensorFlow.
Чтобы построить одномерный тензор, мы будем использовать массив NumPy, который мы создадим, передав встроенный список Python.
import numpy as np tensor_1d = np.array([1.45, -1, 0.2, 102.1])Работа с таким массивом аналогична работе со встроенным списком Python. Основное отличие состоит в том, что массив NumPy также содержит некоторые дополнительные свойства, такие как размер, форма и тип.
> > print tensor1d [ 1.45 -1. 0.2 102.1 ] > > print tensor1d[0] 1.45 > > print tensor1d[2] 0.2 > > print tensor1d.ndim 1 > > print tensor1d.shape (4,) > > print tensor1d.dtype float64Массив NumPy можно легко преобразовать в тензор TensorFlow с помощью вспомогательной функции convert_to_tensor, которая помогает разработчикам преобразовывать объекты Python в тензорные объекты. Эта функция принимает тензорные объекты, массивы NumPy, списки Python и скаляры Python.
tensor = tf.convert_to_tensor(tensor_1d, dtype=tf.float64)Теперь, если мы привяжем наш тензор к сеансу TensorFlow, мы сможем увидеть результаты нашего преобразования.
tensor = tf.convert_to_tensor(tensor_1d, dtype=tf.float64) with tf.Session() as session: print session.run(tensor) print session.run(tensor[0]) print session.run(tensor[1])Выход:
[ 1.45 -1. 0.2 102.1 ] 1.45 -1.0Аналогичным образом мы можем создать двумерный тензор или матрицу:
tensor_2d = np.array(np.random.rand(4, 4), dtype='float32') tensor_2d_1 = np.array(np.random.rand(4, 4), dtype='float32') tensor_2d_2 = np.array(np.random.rand(4, 4), dtype='float32') m1 = tf.convert_to_tensor(tensor_2d) m2 = tf.convert_to_tensor(tensor_2d_1) m3 = tf.convert_to_tensor(tensor_2d_2) mat_product = tf.matmul(m1, m2) mat_sum = tf.add(m2, m3) mat_det = tf.matrix_determinant(m3) with tf.Session() as session: print session.run(mat_product) print session.run(mat_sum) print session.run(mat_det)Тензорные операции
В приведенном выше примере мы вводим несколько операций TensorFlow с векторами и матрицами. Операции выполняют определенные вычисления с тензорами. Какие это расчеты, показано в таблице ниже.
| Оператор TensorFlow | Описание |
|---|---|
| tf.добавить | х+у |
| tf.subtract | ху |
| tf.умножить | х * у |
| tf.div | х/у |
| tf.mod | х % у |
| тс.абс. | |х| |
| tf.отрицательный | -Икс |
| tf.sign | знак (х) |
| тс.кв. | х*х |
| tf.раунд | круглый (х) |
| tf.sqrt | квадрат (х) |
| tf.pow | х^у |
| tf.exp | е^х |
| tf.log | журнал (х) |
| tf.максимум | макс (х, у) |
| tf.минимум | мин (х, у) |
| tf.cos | потому что (х) |
| tf.sin | грех (х) |
Операции TensorFlow, перечисленные в таблице выше, работают с тензорными объектами и выполняются поэлементно. Поэтому, если вы хотите вычислить косинус для вектора x, операция TensorFlow выполнит вычисления для каждого элемента переданного тензора.

tensor_1d = np.array([0, 0, 0]) tensor = tf.convert_to_tensor(tensor_1d, dtype=tf.float64) with tf.Session() as session: print session.run(tf.cos(tensor))Выход:
[ 1. 1. 1.]Матричные операции
Матричные операции очень важны для моделей машинного обучения, таких как линейная регрессия, так как они часто используются в них. TensorFlow поддерживает все наиболее распространенные матричные операции, такие как умножение, транспонирование, инверсия, вычисление определителя, решение линейных уравнений и многое другое.
Далее мы объясним некоторые матричные операции. Они, как правило, важны, когда дело доходит до моделей машинного обучения, например, в линейной регрессии. Давайте напишем код, который будет выполнять базовые операции с матрицами, такие как умножение, получение транспонирования, получение определителя, умножение, решение и многие другие.
Ниже приведены основные примеры вызова этих операций.
import tensorflow as tf import numpy as np def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) m1 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m2 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m3 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m4 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m5 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m_tranpose = tf.transpose(m1) m_mul = tf.matmul(m1, m2) m_det = tf.matrix_determinant(m3) m_inv = tf.matrix_inverse(m4) m_solve = tf.matrix_solve(m5, [[1], [1], [1], [1]]) with tf.Session() as session: print session.run(m_tranpose) print session.run(m_mul) print session.run(m_inv) print session.run(m_det) print session.run(m_solve)Преобразование данных
Снижение
TensorFlow поддерживает различные виды сокращения. Редукция — это операция, которая удаляет одно или несколько измерений из тензора, выполняя определенные операции над этими измерениями. Список поддерживаемых сокращений для текущей версии TensorFlow можно найти здесь. Мы представим некоторые из них в примере ниже.
import tensorflow as tf import numpy as np def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) x = convert( np.array( [ (1, 2, 3), (4, 5, 6), (7, 8, 9) ]), tf.int32) bool_tensor = convert([(True, False, True), (False, False, True), (True, False, False)], tf.bool) red_sum_0 = tf.reduce_sum(x) red_sum = tf.reduce_sum(x, axis=1) red_prod_0 = tf.reduce_prod(x) red_prod = tf.reduce_prod(x, axis=1) red_min_0 = tf.reduce_min(x) red_min = tf.reduce_min(x, axis=1) red_max_0 = tf.reduce_max(x) red_max = tf.reduce_max(x, axis=1) red_mean_0 = tf.reduce_mean(x) red_mean = tf.reduce_mean(x, axis=1) red_bool_all_0 = tf.reduce_all(bool_tensor) red_bool_all = tf.reduce_all(bool_tensor, axis=1) red_bool_any_0 = tf.reduce_any(bool_tensor) red_bool_any = tf.reduce_any(bool_tensor, axis=1) with tf.Session() as session: print "Reduce sum without passed axis parameter: ", session.run(red_sum_0) print "Reduce sum with passed axis=1: ", session.run(red_sum) print "Reduce product without passed axis parameter: ", session.run(red_prod_0) print "Reduce product with passed axis=1: ", session.run(red_prod) print "Reduce min without passed axis parameter: ", session.run(red_min_0) print "Reduce min with passed axis=1: ", session.run(red_min) print "Reduce max without passed axis parameter: ", session.run(red_max_0) print "Reduce max with passed axis=1: ", session.run(red_max) print "Reduce mean without passed axis parameter: ", session.run(red_mean_0) print "Reduce mean with passed axis=1: ", session.run(red_mean) print "Reduce bool all without passed axis parameter: ", session.run(red_bool_all_0) print "Reduce bool all with passed axis=1: ", session.run(red_bool_all) print "Reduce bool any without passed axis parameter: ", session.run(red_bool_any_0) print "Reduce bool any with passed axis=1: ", session.run(red_bool_any)Выход:
Reduce sum without passed axis parameter: 45 Reduce sum with passed axis=1: [ 6 15 24] Reduce product without passed axis parameter: 362880 Reduce product with passed axis=1: [ 6 120 504] Reduce min without passed axis parameter: 1 Reduce min with passed axis=1: [1 4 7] Reduce max without passed axis parameter: 9 Reduce max with passed axis=1: [3 6 9] Reduce mean without passed axis parameter: 5 Reduce mean with passed axis=1: [2 5 8] Reduce bool all without passed axis parameter: False Reduce bool all with passed axis=1: [False False False] Reduce bool any without passed axis parameter: True Reduce bool any with passed axis=1: [ True True True]Первый параметр операторов редукции — это тензор, который мы хотим уменьшить. Второй параметр — это индексы размерностей, по которым мы хотим выполнить приведение. Этот параметр является необязательным, и если его не передать, сокращение будет выполняться по всем измерениям.
Мы можем взглянуть на операцию reduce_sum. Мы передаем двумерный тензор и хотим уменьшить его по размерности 1.
В нашем случае итоговая сумма будет:
[1 + 2 + 3 = 6, 4 + 5 + 6 = 15, 7 + 8 + 9 = 24]Если бы мы передали измерение 0, результат был бы таким:
[1 + 4 + 7 = 12, 2 + 5 + 8 = 15, 3 + 6 + 9 = 18]Если мы не передаем никакую ось, результатом будет просто общая сумма:
1 + 4 + 7 = 12, 2 + 5 + 8 = 15, 3 + 6 + 9 = 45Все функции редукции имеют схожий интерфейс и перечислены в документации по редукции TensorFlow.
Сегментация
Сегментация — это процесс, в котором одним из измерений является процесс сопоставления измерений с предоставленными индексами сегмента, а результирующие элементы определяются строкой индекса.
Сегментация на самом деле группирует элементы по повторяющимся индексам, поэтому, например, в нашем случае у нас есть сегментированные идентификаторы [0, 0, 1, 2, 2] примененные к тензору tens1 , что означает, что первый и второй массивы будут преобразованы после сегментации. операцию (в нашем случае суммирование) и получим новый массив вида (2, 8, 1, 0) = (2+0, 5+3, 3-2, -5+5) . Третий элемент в тензоре tens1 остается нетронутым, так как он не группируется ни по одному повторяющемуся индексу, а последние два массива суммируются так же, как и для первой группы. Помимо суммирования, TensorFlow поддерживает произведение, среднее, максимальное и минимальное значения.
import tensorflow as tf import numpy as np def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) seg_ids = tf.constant([0, 0, 1, 2, 2]) tens1 = convert(np.array([(2, 5, 3, -5), (0, 3, -2, 5), (4, 3, 5, 3), (6, 1, 4, 0), (6, 1, 4, 0)]), tf.int32) tens2 = convert(np.array([1, 2, 3, 4, 5]), tf.int32) seg_sum = tf.segment_sum(tens1, seg_ids) seg_sum_1 = tf.segment_sum(tens2, seg_ids) with tf.Session() as session: print "Segmentation sum tens1: ", session.run(seg_sum) print "Segmentation sum tens2: ", session.run(seg_sum_1) Segmentation sum tens1: [[ 2 8 1 0] [ 4 3 5 3] [12 2 8 0]] Segmentation sum tens2: [3 3 9]Утилиты последовательности
Утилиты последовательности включают такие методы, как:
- функция argmin, которая возвращает индекс с минимальным значением по осям входного тензора,
- функция argmax, которая возвращает индекс с максимальным значением по осям входного тензора,
- setdiff, который вычисляет разницу между двумя списками чисел или строк,
- где функция, которая будет возвращать элементы из двух переданных элементов x или y, что зависит от переданного условия, или
- уникальная функция, которая будет возвращать уникальные элементы в одномерном тензоре.
Мы демонстрируем несколько примеров выполнения ниже:
import numpy as np import tensorflow as tf def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) x = convert(np.array([ [2, 2, 1, 3], [4, 5, 6, -1], [0, 1, 1, -2], [6, 2, 3, 0] ])) y = convert(np.array([1, 2, 5, 3, 7])) z = convert(np.array([1, 0, 4, 6, 2])) arg_min = tf.argmin(x, 1) arg_max = tf.argmax(x, 1) unique = tf.unique(y) diff = tf.setdiff1d(y, z) with tf.Session() as session: print "Argmin = ", session.run(arg_min) print "Argmax = ", session.run(arg_max) print "Unique_values = ", session.run(unique)[0] print "Unique_idx = ", session.run(unique)[1] print "Setdiff_values = ", session.run(diff)[0] print "Setdiff_idx = ", session.run(diff)[1] print session.run(diff)[1]Выход:
Argmin = [2 3 3 3] Argmax = [3 2 1 0] Unique_values = [ 1. 2. 5. 3. 7.] Unique_idx = [0 1 2 3 4] Setdiff_values = [ 5. 3. 7.] Setdiff_idx = [2 3 4]Машинное обучение с TensorFlow
В этом разделе мы представим пример использования машинного обучения с TensorFlow. Первым примером будет алгоритм классификации данных с подходом kNN, а вторым будет использоваться алгоритм линейной регрессии.
kNN
Первый алгоритм — k-ближайших соседей (kNN). Это алгоритм обучения с учителем, который использует показатели расстояния, например евклидово расстояние, для классификации данных по сравнению с обучением. Это один из самых простых алгоритмов, но все же очень мощный для классификации данных. Плюсы этого алгоритма:
- Дает высокую точность, когда обучающая модель достаточно велика, и
- Обычно не чувствителен к выбросам, и нам не нужно делать никаких предположений о данных.
Минусы этого алгоритма:
- Вычислительно дорого и
- Требуется много памяти, когда необходимо добавить новые классифицированные данные ко всем начальным экземплярам обучения.
Расстояние, которое мы будем использовать в этом примере кода, является евклидовым и определяет расстояние между двумя точками следующим образом:
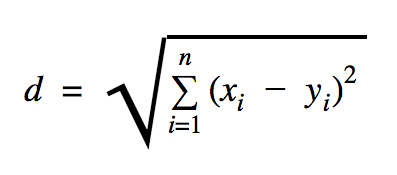
В этой формуле n — количество измерений пространства, x — вектор обучающих данных, а y — новая точка данных, которую мы хотим классифицировать.
import os import numpy as np import tensorflow as tf ccf_train_data = "train_dataset.csv" ccf_test_data = "test_dataset.csv" dataset_dir = os.path.abspath(os.path.join(os.path.dirname(__file__), '../datasets')) ccf_train_filepath = os.path.join(dataset_dir, ccf_train_data) ccf_test_filepath = os.path.join(dataset_dir, ccf_test_data) def load_data(filepath): from numpy import genfromtxt csv_data = genfromtxt(filepath, delimiter=",", skip_header=1) data = [] labels = [] for d in csv_data: data.append(d[:-1]) labels.append(d[-1]) return np.array(data), np.array(labels) train_dataset, train_labels = load_data(ccf_train_filepath) test_dataset, test_labels = load_data(ccf_test_filepath) train_pl = tf.placeholder("float", [None, 28]) test_pl = tf.placeholder("float", [28]) knn_prediction = tf.reduce_sum(tf.abs(tf.add(train_pl, tf.negative(test_pl))), axis=1) pred = tf.argmin(knn_prediction, 0) with tf.Session() as tf_session: missed = 0 for i in xrange(len(test_dataset)): knn_index = tf_session.run(pred, feed_dict={train_pl: train_dataset, test_pl: test_dataset[i]}) print "Predicted class {} -- True class {}".format(train_labels[knn_index], test_labels[i]) if train_labels[knn_index] != test_labels[i]: missed += 1 tf.summary.FileWriter("../samples/article/logs", tf_session.graph) print "Missed: {} -- Total: {}".format(missed, len(test_dataset))Набор данных, который мы использовали в приведенном выше примере, можно найти в разделе наборов данных Kaggle. Мы использовали тот, который содержит транзакции, совершенные по кредитным картам европейских держателей карт. Мы используем данные без какой-либо очистки или фильтрации, и, согласно описанию в Kaggle для этого набора данных, они сильно несбалансированы. Набор данных содержит 31 переменную: время, V1, …, V28, количество и класс. В этом примере кода мы используем только V1, …, V28 и Class. Класс помечает мошеннические транзакции цифрой 1, а немошеннические — цифрой 0.
Пример кода содержит в основном то, что мы описали в предыдущих разделах, за исключением того, где мы представили функцию загрузки набора данных. Функция load_data(filepath) примет файл CSV в качестве аргумента и вернет кортеж с данными и метками, определенными в CSV.
Чуть ниже этой функции мы определили заполнители для тестовых и обученных данных. Обученные данные используются в модели прогнозирования для определения меток входных данных, которые необходимо классифицировать. В нашем случае kNN использует евклидово расстояние для получения ближайшей метки.
Коэффициент ошибок можно рассчитать простым делением на число, когда классификатор пропустил, на общее количество примеров, которое в нашем случае для этого набора данных равно 0,2 (т. е. классификатор дает нам неправильную метку данных для 20% тестовых данных).
Линейная регрессия
Алгоритм линейной регрессии ищет линейную связь между двумя переменными. Если мы пометим зависимую переменную как y, а независимую переменную как x, то мы попытаемся оценить параметры функции y = Wx + b .
Линейная регрессия — широко используемый алгоритм в области прикладных наук. Этот алгоритм позволяет добавить в реализацию два важных понятия машинного обучения: функцию стоимости и метод градиентного спуска для нахождения минимума функции.
Алгоритм машинного обучения, реализованный с использованием этого метода, должен предсказывать значения y как функцию x , где алгоритм линейной регрессии будет определять значения W и b , которые на самом деле неизвестны и определяются в процессе обучения. Выбирается функция стоимости, и обычно используется среднеквадратическая ошибка, где градиентный спуск представляет собой алгоритм оптимизации, используемый для нахождения локального минимума функции стоимости.
Метод градиентного спуска — это только локальный минимум функции, но его можно использовать для поиска глобального минимума, случайным образом выбирая новую начальную точку после нахождения локального минимума и повторяя этот процесс много раз. Если количество минимумов функции ограничено и количество попыток очень велико, то есть большая вероятность, что в какой-то момент будет обнаружен глобальный минимум. Некоторые подробности об этой технике мы оставим для статьи, которую мы упоминали во вступительной части.
import tensorflow as tf import numpy as np test_data_size = 2000 iterations = 10000 learn_rate = 0.005 def generate_test_values(): train_x = [] train_y = [] for _ in xrange(test_data_size): x1 = np.random.rand() x2 = np.random.rand() x3 = np.random.rand() y_f = 2 * x1 + 3 * x2 + 7 * x3 + 4 train_x.append([x1, x2, x3]) train_y.append(y_f) return np.array(train_x), np.transpose([train_y]) x = tf.placeholder(tf.float32, [None, 3], name="x") W = tf.Variable(tf.zeros([3, 1]), name="W") b = tf.Variable(tf.zeros([1]), name="b") y = tf.placeholder(tf.float32, [None, 1]) model = tf.add(tf.matmul(x, W), b) cost = tf.reduce_mean(tf.square(y - model)) train = tf.train.GradientDescentOptimizer(learn_rate).minimize(cost) train_dataset, train_values = generate_test_values() init = tf.global_variables_initializer() with tf.Session() as session: session.run(init) for _ in xrange(iterations): session.run(train, feed_dict={ x: train_dataset, y: train_values }) print "cost = {}".format(session.run(cost, feed_dict={ x: train_dataset, y: train_values })) print "W = {}".format(session.run(W)) print "b = {}".format(session.run(b))Выход:
cost = 3.1083032809e-05 W = [[ 1.99049103] [ 2.9887135 ] [ 6.98754263]] b = [ 4.01742554] В приведенном выше примере у нас есть две новые переменные, которые мы назвали cost и train . С этими двумя переменными мы определили оптимизатор, который мы хотим использовать в нашей модели обучения, и функцию, которую мы хотим минимизировать.
В конце выходные параметры W и b должны быть идентичны параметрам, определенным в функции generate_test_values . В строке 17 мы фактически определили функцию, которую мы использовали для генерации точек линейных данных для обучения, где w1=2 , w2=3 , w3=7 и b=4 . Линейная регрессия из приведенного выше примера является многомерной, в которой используется более одной независимой переменной.
Заключение
Как вы можете видеть из этого руководства по TensorFlow, TensorFlow — это мощная платформа, которая упрощает работу с математическими выражениями и многомерными массивами — что принципиально необходимо в машинном обучении. Он также абстрагируется от сложностей выполнения графиков данных и масштабирования.
Со временем популярность TensorFlow выросла, и теперь разработчики используют ее для решения задач с использованием методов глубокого обучения для распознавания изображений, обнаружения видео, обработки текста, например анализа тональности, и т. д. Как и с любой другой библиотекой, вам может потребоваться некоторое время, чтобы привыкнуть. к концепциям, на которых построен TensorFlow. И, как только вы это сделаете, с помощью документации и поддержки сообщества представление проблем в виде графиков данных и их решение с помощью TensorFlow может сделать машинное обучение в масштабе менее утомительным процессом.
