TensorFlow入門:機械学習チュートリアル
公開: 2022-03-11TensorFlowは、Googleによって作成されたオープンソースのソフトウェアライブラリであり、機械学習と深層学習システムの実装に使用されます。 これらの2つの名前には、共通の課題を共有する一連の強力なアルゴリズムが含まれています。これにより、コンピューターは、複雑なパターンを自動的に検出する方法や、可能な限り最良の決定を行う方法を学習できます。
これらのシステムの詳細に興味がある場合は、機械学習とディープラーニングに関するToptalのブログ投稿から詳細を学ぶことができます。
TensorFlowは、その中心にあるデータフロープログラミング用のライブラリです。 さまざまな最適化手法を活用して、数式の計算をより簡単でパフォーマンスの高いものにします。
TensorFlowの主な機能のいくつかは次のとおりです。
- 多次元配列を含む数式を効率的に処理します
- ディープニューラルネットワークと機械学習の概念の優れたサポート
- 両方のアーキテクチャで同じコードを実行できるGPU/CPUコンピューティング
- マシンおよび巨大なデータセット間での計算の高いスケーラビリティ
これらの機能を組み合わせることで、TensorFlowは本番規模のマシンインテリジェンスに最適なフレームワークになります。
このTensorFlowチュートリアルでは、TensorFlowでシンプルでありながら強力な機械学習メソッドを使用する方法と、補助ライブラリの一部を使用して、TensorFlowで作成されたモデルをデバッグ、視覚化、微調整する方法を学習します。
TensorFlowのインストール
Python2.7およびPython3.3以降で動作するTensorFlowPythonAPIを使用します。 GPUバージョン(Linuxのみ)には、CudaToolkit7.0以降とcuDNNv2+が必要です。
Condaパッケージの依存関係管理システムを使用してTensorFlowをインストールします。 Condaを使用すると、マシン上の複数の環境を分離できます。 ここからCondaのインストール方法を学ぶことができます。
Condaをインストールした後、TensorFlowのインストールと使用に使用する環境を作成できます。 次のコマンドは、NumPyなどの追加ライブラリを使用して環境を作成します。これは、TensorFlowの使用を開始すると非常に便利です。
この環境内にインストールされているPythonのバージョンは2.7であり、この記事ではこのバージョンを使用します。
conda create --name TensorflowEnv biopython 簡単にするために、NumPyだけでなくbiopythonをここにインストールしています。 これには、NumPyと私たちが必要とする他のいくつかのパッケージが含まれます。 conda install pip installを使用して、必要に応じていつでもパッケージをインストールできます。
次のコマンドは、作成されたConda環境をアクティブにします。 グローバルにインストールされているパッケージや他の環境にインストールされているパッケージと混同することなく、その中にインストールされているパッケージを使用できるようになります。
source activate TensorFlowEnvpipインストールツールは、Conda環境の標準部分です。 これを使用してTensorFlowライブラリをインストールします。 それを行う前に、次のコマンドを使用して、pipを最新バージョンに更新することをお勧めします。
pip install --upgrade pipこれで、次のコマンドを実行してTensorFlowをインストールする準備が整いました。
pip install tensorflowTensorFlowのダウンロードとビルドには数分かかる場合があります。 執筆時点では、これによりTensorFlow1.1.0がインストールされます。
データフローグラフ
TensorFlowでは、データフローグラフを使用して計算が記述されます。 グラフの各ノードは、数学演算(加算、除算、乗算など)のインスタンスを表し、各エッジは、演算が実行される多次元データセット(テンサー)です。
TensorFlowは計算グラフを処理するため、各ノードが0個以上の入力と0個以上の出力を持つ操作のインスタンス化を表す場合に管理されます。
TensorFlowのエッジは、2つのカテゴリにグループ化できます。1つの操作の出力が別の操作の入力になる可能性がある通常のエッジ転送データ構造(テンソル)と、2つのノード間の依存関係を制御して設定するために使用される特別なエッジです。 1つのノードが別のノードの終了を待機する操作の順序。
単純な表現
TensorFlowの要素について説明する前に、まずTensorFlowを操作するセッションを実行して、TensorFlowプログラムがどのように見えるかを理解します。
簡単な式から始めて、何らかの理由で、関数y = 5*x + 13をTensorFlow形式で評価したいとします。
単純なPythonコードでは、次のようになります。
x = -2.0 y = 5*x + 13 print yこの場合、結果は3.0になります。
次に、上記の式をTensorFlowの用語に変換します。
定数
TensorFlowでは、定数は、署名constant(value, dtype=None, shape=None, name='Const', verify_shape=False)を持つ関数constantを使用して作成されます。ここで、 valueは、で使用される実際の定数値です。さらに計算すると、 dtypeはデータ型パラメーター(float32 / 64、int8 / 16など)、 shapeはオプションのディメンション、 nameはテンソルのオプションの名前、最後のパラメーターはブール値であり、値の形。
トレーニングモデル内で特定の値を持つ定数が必要な場合は、次の例のようにconstantオブジェクトを使用できます。
z = tf.constant(5.2, name="x", dtype=tf.float32)変数
TensorFlowの変数は、セッション全体で状態を維持するために明示的に初期化してグラフ内で使用する必要があるテンソルを含むメモリ内バッファです。 コンストラクターを呼び出すだけで、変数が計算グラフに追加されます。
変数は、トレーニングモデルを開始すると特に便利であり、パラメーターを保持および更新するために使用されます。 コンストラクターの引数として渡される初期値は、テンソルとして変換または返されることができるテンソルまたはオブジェクトを表します。 つまり、後でトレーニングプロセスで使用され、反復で更新される事前定義された値またはランダムな値を変数に入力する場合は、次の方法で定義できます。
k = tf.Variable(tf.zeros([1]), name="k")TensorFlowで変数を使用する別の方法は、その変数がトレーニング可能ではなく、次の方法で定義できる計算です。
k = tf.Variable(tf.add(a, b), trainable=False)セッション
実際にノードを評価するには、セッション内で計算グラフを実行する必要があります。
セッションは、TensorFlowランタイムの制御と状態をカプセル化します。 パラメータのないセッションは、現在のセッションで作成されたデフォルトのグラフを使用します。それ以外の場合、セッションクラスは、実行されるそのセッションで使用されるグラフパラメータを受け入れます。
以下は、上記で定義された用語をTensorFlowで使用して、単純な線形関数を計算する方法を示す簡単なコードスニペットです。
import tensorflow as tf x = tf.constant(-2.0, name="x", dtype=tf.float32) a = tf.constant(5.0, name="a", dtype=tf.float32) b = tf.constant(13.0, name="b", dtype=tf.float32) y = tf.Variable(tf.add(tf.multiply(a, x), b)) init = tf.global_variables_initializer() with tf.Session() as session: session.run(init) print session.run(y)TensorFlowの使用:計算グラフの定義
データフローグラフを操作することの良い点は、実行モデルがその実行から分離されていることです(CPU、GPU、またはいくつかの組み合わせで)。実装されると、TensorFlowのソフトウェアをCPUまたはGPUで使用でき、コードに関連するすべての複雑さが発生します。実行は非表示になっています。
計算グラフは、Graphオブジェクトを明示的にインスタンス化することなく、TensorFlowライブラリを使用するプロセスで構築できます。
TensorFlowのGraphオブジェクトは、 c = tf.add(a, b)ような単純なコード行の結果として作成できます。 これにより、合計cを出力として生成する2つのテンソルaとbを受け取る操作ノードが作成されます。
計算グラフは、グラフオブジェクトを直接呼び出す必要なしにライブラリを使用する組み込みプロセスです。 データの単位として一連の操作とテンソルを含むTensorFlowのグラフオブジェクトは、同じプロセスを可能にし、各グラフが異なるセッションに割り当てられる複数のグラフを含む操作間で使用されます。 たとえば、コードc = tf.add(a, b)の単純な行は、2つのテンソルaとbを入力として受け取り、それらの合計cを出力として生成する操作ノードを作成します。
TensorFlowは、グラフ内の任意の操作にテンソルをパッチするためのフィードメカニズムも提供します。このフィードでは、操作の出力がテンソル値に置き換えられます。 フィードデータは、 run()関数呼び出しで引数として渡されます。
プレースホルダーは、開発者がいくつかの式の内部にバインドされているプレースホルダーを介して計算グラフにデータを挿入できるようにするTensorFlowの方法です。 プレースホルダーの署名は次のとおりです。
placeholder(dtype, shape=None, name=None)ここで、dtypeはテンソル内の要素のタイプであり、供給されるテンソルの形状と操作の名前の両方を提供できます。
形状が通過しない場合、このテンソルは任意の形状でフィードできます。 重要な注意点は、プレースホルダーテンソルにデータを供給する必要があることです。そうしないと、セッションの実行時に、その部分が欠落している場合、プレースホルダーは次の構造でエラーを生成します。
InvalidArgumentError (see above for traceback): You must feed a value for placeholder tensor 'y' with dtype floatプレースホルダーの利点は、開発者が事前にデータを提供しなくても操作や一般的な計算グラフを作成できることと、外部ソースから実行時にデータを追加できることです。
TensorFlow方式で2つの整数xとyを乗算するという単純な問題を考えてみましょう。ここでは、プレースホルダーがセッションrunメソッドを介してフィードメカニズムと一緒に使用されます。
import tensorflow as tf x = tf.placeholder(tf.float32, name="x") y = tf.placeholder(tf.float32, name="y") z = tf.multiply(x, y, name="z") with tf.Session() as session: print session.run(z, feed_dict={x: 2.1, y: 3.0})TensorBoardを使用した計算グラフの視覚化
TensorBoardは、データフローグラフを分析するための視覚化ツールです。 これは、機械学習モデルをよりよく理解するのに役立ちます。
TensorBoardを使用すると、パラメータに関するさまざまなタイプの統計と、一般的な計算グラフの部分に関する詳細についての洞察を得ることができます。 深いニューラルネットワークに多数のノードがあることは珍しいことではありません。 TensorBoardを使用すると、開発者は各ノードと、TensorFlowランタイムで計算がどのように実行されるかについての洞察を得ることができます。
ここで、このTensorFlowチュートリアルの最初から、 y = a*x + bの形式で線形関数を定義した例に戻りましょう。
後でTensorBoardで使用できるセッションからのイベントをログに記録するために、TensorFlowはFileWriterクラスを提供します。 これを使用して、コンストラクターが6つのパラメーターを受け入れ、次のような要約を格納するためのイベントファイルを作成できます。
__init__(logdir, graph=None, max_queue=10, flush_secs=120, graph_def=None, filename_suffix=None)ここで、logdirパラメーターは必須であり、その他にはデフォルト値があります。 グラフパラメータは、トレーニングプログラムで作成されたセッションオブジェクトから渡されます。 完全なサンプルコードは次のようになります。
import tensorflow as tf x = tf.constant(-2.0, name="x", dtype=tf.float32) a = tf.constant(5.0, name="a", dtype=tf.float32) b = tf.constant(13.0, name="b", dtype=tf.float32) y = tf.Variable(tf.add(tf.multiply(a, x), b)) init = tf.global_variables_initializer() with tf.Session() as session: merged = tf.summary.merge_all() // new writer = tf.summary.FileWriter("logs", session.graph) // new session.run(init) print session.run(y) 2行だけ追加しました。 デフォルトのグラフに収集されたすべての要約をマージし、上記で説明したように、 FileWriterを使用してイベントをファイルにダンプします。
プログラムを実行した後、ディレクトリログにファイルがあり、最後のステップはtensorboardを実行することです。
tensorboard --logdir logs/ これで、TensorBoardが起動し、デフォルトのポート6006で実行されますhttp://localhost:6006を開いて[グラフ]メニュー項目(ページの上部にあります)をクリックすると、次のようなグラフが表示されます。下の写真で:
TensorBoardは、以下で説明する定数とサマリーノード固有のシンボルをマークします。
TensorFlowを使用した数学
テンソルはTensorFlowの基本的なデータ構造であり、データフローグラフの接続エッジを表します。
テンソルは、多次元配列またはリストを識別するだけです。 テンソル構造は、ランク、形状、タイプの3つのパラメーターで識別できます。
- ランク:テンソルの次元数を識別します。 ランクは、テンソルの次数またはn次元として知られています。たとえば、ランク1のテンソルはベクトル、ランク2のテンソルは行列です。
- 形状:テンソルの形状は、テンソルが持つ行と列の数です。
- タイプ:テンソル要素に割り当てられたデータタイプ。
TensorFlowでテンソルを構築するために、n次元配列を構築できます。 これは、NumPyライブラリを使用するか、Pythonのn次元配列をTensorFlowテンソルに変換することで簡単に実行できます。
1次元テンソルを構築するには、NumPy配列を使用します。これは、組み込みのPythonリストを渡すことで構築します。
import numpy as np tensor_1d = np.array([1.45, -1, 0.2, 102.1])この種の配列を操作することは、組み込みのPythonリストを操作することに似ています。 主な違いは、NumPy配列には、寸法、形状、タイプなどの追加のプロパティも含まれていることです。
> > print tensor1d [ 1.45 -1. 0.2 102.1 ] > > print tensor1d[0] 1.45 > > print tensor1d[2] 0.2 > > print tensor1d.ndim 1 > > print tensor1d.shape (4,) > > print tensor1d.dtype float64NumPy配列は、補助関数convert_to_tensorを使用してTensorFlowテンソルに簡単に変換できます。これは、開発者がPythonオブジェクトをテンソルオブジェクトに変換するのに役立ちます。 この関数は、テンソルオブジェクト、NumPy配列、Pythonリスト、およびPythonスカラーを受け入れます。
tensor = tf.convert_to_tensor(tensor_1d, dtype=tf.float64)これで、テンソルをTensorFlowセッションにバインドすると、変換の結果を確認できるようになります。
tensor = tf.convert_to_tensor(tensor_1d, dtype=tf.float64) with tf.Session() as session: print session.run(tensor) print session.run(tensor[0]) print session.run(tensor[1])出力:
[ 1.45 -1. 0.2 102.1 ] 1.45 -1.0同様の方法で、2次元テンソルまたは行列を作成できます。
tensor_2d = np.array(np.random.rand(4, 4), dtype='float32') tensor_2d_1 = np.array(np.random.rand(4, 4), dtype='float32') tensor_2d_2 = np.array(np.random.rand(4, 4), dtype='float32') m1 = tf.convert_to_tensor(tensor_2d) m2 = tf.convert_to_tensor(tensor_2d_1) m3 = tf.convert_to_tensor(tensor_2d_2) mat_product = tf.matmul(m1, m2) mat_sum = tf.add(m2, m3) mat_det = tf.matrix_determinant(m3) with tf.Session() as session: print session.run(mat_product) print session.run(mat_sum) print session.run(mat_det)テンソル演算
上記の例では、ベクトルと行列に対するTensorFlow操作をいくつか紹介します。 演算はテンソルに対して特定の計算を実行します。 それらがどの計算であるかを以下の表に示します。
| TensorFlowオペレーター | 説明 |
|---|---|
| tf.add | x + y |
| tf.subtract | xy |
| tf.multiply | x * y |
| tf.div | x / y |
| tf.mod | x%y |
| tf.abs | | x | |
| tf.negative | -バツ |
| tf.sign | sign(x) |
| tf.square | x * x |
| tf.round | round(x) |
| tf.sqrt | sqrt(x) |
| tf.pow | x ^ y |
| tf.exp | e ^ x |
| tf.log | log(x) |
| tf.maximum | max(x、y) |
| tf.minimum | min(x、y) |
| tf.cos | cos(x) |
| tf.sin | sin(x) |
上記の表にリストされているTensorFlow操作は、テンソルオブジェクトで機能し、要素ごとに実行されます。 したがって、ベクトルxの正弦を計算する場合、TensorFlow演算は、渡されたテンソルの各要素に対して計算を実行します。
tensor_1d = np.array([0, 0, 0]) tensor = tf.convert_to_tensor(tensor_1d, dtype=tf.float64) with tf.Session() as session: print session.run(tf.cos(tensor))出力:
[ 1. 1. 1.]行列演算
行列演算は、線形回帰などの機械学習モデルでよく使用されるため、機械学習モデルにとって非常に重要です。 TensorFlowは、乗算、転置、反転、行列式の計算、線形方程式の解法など、最も一般的なすべての行列演算をサポートしています。
次に、いくつかの行列演算について説明します。 線形回帰のように、機械学習モデルに関しては、これらは重要になる傾向があります。 乗算、転置の取得、行列式の取得、乗算、solなどの基本的な行列演算を実行するコードを記述しましょう。

以下は、これらの操作を呼び出す基本的な例です。
import tensorflow as tf import numpy as np def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) m1 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m2 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m3 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m4 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m5 = convert(np.array(np.random.rand(4, 4), dtype='float32')) m_tranpose = tf.transpose(m1) m_mul = tf.matmul(m1, m2) m_det = tf.matrix_determinant(m3) m_inv = tf.matrix_inverse(m4) m_solve = tf.matrix_solve(m5, [[1], [1], [1], [1]]) with tf.Session() as session: print session.run(m_tranpose) print session.run(m_mul) print session.run(m_inv) print session.run(m_det) print session.run(m_solve)データの変換
割引
TensorFlowは、さまざまな種類の削減をサポートしています。 リダクションは、テンソルから1つ以上の次元を削除する操作であり、これらの次元全体で特定の操作を実行します。 TensorFlowの現在のバージョンでサポートされている削減のリストは、ここにあります。 以下の例では、それらのいくつかを紹介します。
import tensorflow as tf import numpy as np def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) x = convert( np.array( [ (1, 2, 3), (4, 5, 6), (7, 8, 9) ]), tf.int32) bool_tensor = convert([(True, False, True), (False, False, True), (True, False, False)], tf.bool) red_sum_0 = tf.reduce_sum(x) red_sum = tf.reduce_sum(x, axis=1) red_prod_0 = tf.reduce_prod(x) red_prod = tf.reduce_prod(x, axis=1) red_min_0 = tf.reduce_min(x) red_min = tf.reduce_min(x, axis=1) red_max_0 = tf.reduce_max(x) red_max = tf.reduce_max(x, axis=1) red_mean_0 = tf.reduce_mean(x) red_mean = tf.reduce_mean(x, axis=1) red_bool_all_0 = tf.reduce_all(bool_tensor) red_bool_all = tf.reduce_all(bool_tensor, axis=1) red_bool_any_0 = tf.reduce_any(bool_tensor) red_bool_any = tf.reduce_any(bool_tensor, axis=1) with tf.Session() as session: print "Reduce sum without passed axis parameter: ", session.run(red_sum_0) print "Reduce sum with passed axis=1: ", session.run(red_sum) print "Reduce product without passed axis parameter: ", session.run(red_prod_0) print "Reduce product with passed axis=1: ", session.run(red_prod) print "Reduce min without passed axis parameter: ", session.run(red_min_0) print "Reduce min with passed axis=1: ", session.run(red_min) print "Reduce max without passed axis parameter: ", session.run(red_max_0) print "Reduce max with passed axis=1: ", session.run(red_max) print "Reduce mean without passed axis parameter: ", session.run(red_mean_0) print "Reduce mean with passed axis=1: ", session.run(red_mean) print "Reduce bool all without passed axis parameter: ", session.run(red_bool_all_0) print "Reduce bool all with passed axis=1: ", session.run(red_bool_all) print "Reduce bool any without passed axis parameter: ", session.run(red_bool_any_0) print "Reduce bool any with passed axis=1: ", session.run(red_bool_any)出力:
Reduce sum without passed axis parameter: 45 Reduce sum with passed axis=1: [ 6 15 24] Reduce product without passed axis parameter: 362880 Reduce product with passed axis=1: [ 6 120 504] Reduce min without passed axis parameter: 1 Reduce min with passed axis=1: [1 4 7] Reduce max without passed axis parameter: 9 Reduce max with passed axis=1: [3 6 9] Reduce mean without passed axis parameter: 5 Reduce mean with passed axis=1: [2 5 8] Reduce bool all without passed axis parameter: False Reduce bool all with passed axis=1: [False False False] Reduce bool any without passed axis parameter: True Reduce bool any with passed axis=1: [ True True True]削減演算子の最初のパラメーターは、削減したいテンソルです。 2番目のパラメーターは、縮小を実行するディメンションのインデックスです。 このパラメータはオプションであり、渡されない場合、削減はすべての次元に沿って実行されます。
reduce_sum操作を見てみましょう。 2次元テンソルを渡し、次元1に沿ってそれを減らしたいと考えています。
この場合、結果の合計は次のようになります。
[1 + 2 + 3 = 6, 4 + 5 + 6 = 15, 7 + 8 + 9 = 24]次元0を渡した場合、結果は次のようになります。
[1 + 4 + 7 = 12, 2 + 5 + 8 = 15, 3 + 6 + 9 = 18]軸を通過しない場合、結果は次の合計になります。
1 + 4 + 7 = 12, 2 + 5 + 8 = 15, 3 + 6 + 9 = 45すべてのリダクション関数は同様のインターフェースを備えており、TensorFlowリダクションドキュメントにリストされています。
セグメンテーション
セグメンテーションは、ディメンションの1つが、提供されたセグメントインデックスにディメンションをマッピングするプロセスであり、結果の要素はインデックス行によって決定されるプロセスです。
セグメンテーションは実際には繰り返されるインデックスの下で要素をグループ化するため、たとえば、この場合、テンソルtens1に適用されるセグメント化されたID [0, 0, 1, 2, 2]があります。つまり、1番目と2番目の配列はセグメンテーションに続いて変換されます。操作(この場合は合計)を実行すると(2, 8, 1, 0) = (2+0, 5+3, 3-2, -5+5)のような新しい配列が取得されます。 テンソルtens1の3番目の要素は、繰り返されるインデックスにグループ化されていないため、変更されていません。最後の2つの配列は、最初のグループの場合と同じ方法で合計されます。 合計に加えて、TensorFlowは積、平均、最大、最小をサポートします。
import tensorflow as tf import numpy as np def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) seg_ids = tf.constant([0, 0, 1, 2, 2]) tens1 = convert(np.array([(2, 5, 3, -5), (0, 3, -2, 5), (4, 3, 5, 3), (6, 1, 4, 0), (6, 1, 4, 0)]), tf.int32) tens2 = convert(np.array([1, 2, 3, 4, 5]), tf.int32) seg_sum = tf.segment_sum(tens1, seg_ids) seg_sum_1 = tf.segment_sum(tens2, seg_ids) with tf.Session() as session: print "Segmentation sum tens1: ", session.run(seg_sum) print "Segmentation sum tens2: ", session.run(seg_sum_1) Segmentation sum tens1: [[ 2 8 1 0] [ 4 3 5 3] [12 2 8 0]] Segmentation sum tens2: [3 3 9]シーケンスユーティリティ
シーケンスユーティリティには、次のようなメソッドが含まれます。
- argmin関数は、入力テンソルの軸全体で最小値を持つインデックスを返します。
- argmax関数は、入力テンソルの軸全体で最大値のインデックスを返します。
- setdiffは、数値または文字列の2つのリスト間の差を計算します。
- where関数は、渡された条件に応じて、渡された2つの要素xまたはyから要素を返します。
- 1次元テンソルで一意の要素を返す一意の関数。
以下にいくつかの実行例を示します。
import numpy as np import tensorflow as tf def convert(v, t=tf.float32): return tf.convert_to_tensor(v, dtype=t) x = convert(np.array([ [2, 2, 1, 3], [4, 5, 6, -1], [0, 1, 1, -2], [6, 2, 3, 0] ])) y = convert(np.array([1, 2, 5, 3, 7])) z = convert(np.array([1, 0, 4, 6, 2])) arg_min = tf.argmin(x, 1) arg_max = tf.argmax(x, 1) unique = tf.unique(y) diff = tf.setdiff1d(y, z) with tf.Session() as session: print "Argmin = ", session.run(arg_min) print "Argmax = ", session.run(arg_max) print "Unique_values = ", session.run(unique)[0] print "Unique_idx = ", session.run(unique)[1] print "Setdiff_values = ", session.run(diff)[0] print "Setdiff_idx = ", session.run(diff)[1] print session.run(diff)[1]出力:
Argmin = [2 3 3 3] Argmax = [3 2 1 0] Unique_values = [ 1. 2. 5. 3. 7.] Unique_idx = [0 1 2 3 4] Setdiff_values = [ 5. 3. 7.] Setdiff_idx = [2 3 4]TensorFlowを使用した機械学習
このセクションでは、TensorFlowを使用した機械学習のユースケースを紹介します。 最初の例はkNNアプローチでデータを分類するためのアルゴリズムであり、2番目の例は線形回帰アルゴリズムを使用します。
kNN
最初のアルゴリズムはk最近傍法(kNN)です。 これは、ユークリッド距離などの距離メトリックを使用して、トレーニングに対してデータを分類する教師あり学習アルゴリズムです。 これは最も単純なアルゴリズムの1つですが、それでもデータの分類には非常に強力です。 このアルゴリズムの長所:
- トレーニングモデルが十分に大きい場合に高精度を提供し、
- 通常、外れ値に敏感ではなく、データについての仮定をする必要はありません。
このアルゴリズムの短所:
- 計算コストが高く、
- すべての初期トレーニングインスタンスに新しい分類データを追加する必要がある場合は、大量のメモリが必要です。
このコードサンプルで使用する距離はユークリッドであり、次のように2点間の距離を定義します。
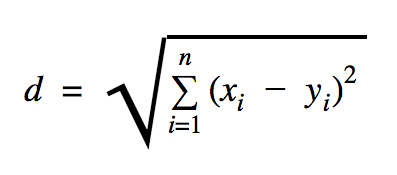
この式で、 nは空間の次元数、 xはトレーニングデータのベクトル、 yは分類する新しいデータポイントです。
import os import numpy as np import tensorflow as tf ccf_train_data = "train_dataset.csv" ccf_test_data = "test_dataset.csv" dataset_dir = os.path.abspath(os.path.join(os.path.dirname(__file__), '../datasets')) ccf_train_filepath = os.path.join(dataset_dir, ccf_train_data) ccf_test_filepath = os.path.join(dataset_dir, ccf_test_data) def load_data(filepath): from numpy import genfromtxt csv_data = genfromtxt(filepath, delimiter=",", skip_header=1) data = [] labels = [] for d in csv_data: data.append(d[:-1]) labels.append(d[-1]) return np.array(data), np.array(labels) train_dataset, train_labels = load_data(ccf_train_filepath) test_dataset, test_labels = load_data(ccf_test_filepath) train_pl = tf.placeholder("float", [None, 28]) test_pl = tf.placeholder("float", [28]) knn_prediction = tf.reduce_sum(tf.abs(tf.add(train_pl, tf.negative(test_pl))), axis=1) pred = tf.argmin(knn_prediction, 0) with tf.Session() as tf_session: missed = 0 for i in xrange(len(test_dataset)): knn_index = tf_session.run(pred, feed_dict={train_pl: train_dataset, test_pl: test_dataset[i]}) print "Predicted class {} -- True class {}".format(train_labels[knn_index], test_labels[i]) if train_labels[knn_index] != test_labels[i]: missed += 1 tf.summary.FileWriter("../samples/article/logs", tf_session.graph) print "Missed: {} -- Total: {}".format(missed, len(test_dataset))上記の例で使用したデータセットは、Kaggleデータセットセクションにあります。 ヨーロッパのカード所有者のクレジットカードによる取引を含むものを使用しました。 クリーニングやフィルタリングを行わずにデータを使用しており、このデータセットのKaggleの説明によると、データは非常に不均衡です。 データセットには、Time、V1、…、V28、Amount、およびClassの31個の変数が含まれています。 このコードサンプルでは、V1、…、V28およびClassのみを使用しています。 クラスは、不正なトランザクションを1で、そうでないトランザクションを0でラベル付けします。
コードサンプルには、データセットをロードするための関数を導入した場合を除いて、前のセクションで説明したものがほとんど含まれています。 関数load_data(filepath)は、引数としてCSVファイルを受け取り、CSVで定義されたデータとラベルを持つタプルを返します。
その関数のすぐ下に、テストデータとトレーニング済みデータのプレースホルダーを定義しました。 トレーニングされたデータは、分類する必要のある入力データのラベルを解決するために予測モデルで使用されます。 この場合、kNNはユークリッド距離を使用して最も近いラベルを取得します。
エラー率は、分類器が欠落した場合の数を、このデータセットの場合は0.2である例の総数で単純に除算することで計算できます(つまり、分類器は、テストデータの20%に対して間違ったデータラベルを提供します)。
線形回帰
線形回帰アルゴリズムは、2つの変数間の線形関係を探します。 従属変数にyのラベルを付け、独立変数にxのラベルを付ける場合、関数y = Wx + bのパラメーターを推定しようとしています。
線形回帰は、応用科学の分野で広く使用されているアルゴリズムです。 このアルゴリズムにより、機械学習の2つの重要な概念を実装に追加できます。コスト関数と関数の最小値を見つけるための最急降下法です。
この方法を使用して実装される機械学習アルゴリズムは、 xの関数としてyの値を予測する必要があります。ここで、線形回帰アルゴリズムは、実際には未知であり、トレーニングプロセス全体で決定される値Wとbを決定します。 コスト関数が選択され、通常、平均二乗誤差が使用されます。ここで、勾配降下法は、コスト関数の極小値を見つけるために使用される最適化アルゴリズムです。
最急降下法は極小値にすぎませんが、極小値を見つけたら新しい開始点をランダムに選択し、このプロセスを何度も繰り返すことで、大域的最小値の検索に使用できます。 関数の最小値の数が制限されており、試行回数が非常に多い場合は、ある時点でグローバル最小値が検出される可能性が高くなります。 この手法の詳細については、紹介セクションで説明した記事に残しておきます。
import tensorflow as tf import numpy as np test_data_size = 2000 iterations = 10000 learn_rate = 0.005 def generate_test_values(): train_x = [] train_y = [] for _ in xrange(test_data_size): x1 = np.random.rand() x2 = np.random.rand() x3 = np.random.rand() y_f = 2 * x1 + 3 * x2 + 7 * x3 + 4 train_x.append([x1, x2, x3]) train_y.append(y_f) return np.array(train_x), np.transpose([train_y]) x = tf.placeholder(tf.float32, [None, 3], name="x") W = tf.Variable(tf.zeros([3, 1]), name="W") b = tf.Variable(tf.zeros([1]), name="b") y = tf.placeholder(tf.float32, [None, 1]) model = tf.add(tf.matmul(x, W), b) cost = tf.reduce_mean(tf.square(y - model)) train = tf.train.GradientDescentOptimizer(learn_rate).minimize(cost) train_dataset, train_values = generate_test_values() init = tf.global_variables_initializer() with tf.Session() as session: session.run(init) for _ in xrange(iterations): session.run(train, feed_dict={ x: train_dataset, y: train_values }) print "cost = {}".format(session.run(cost, feed_dict={ x: train_dataset, y: train_values })) print "W = {}".format(session.run(W)) print "b = {}".format(session.run(b))出力:
cost = 3.1083032809e-05 W = [[ 1.99049103] [ 2.9887135 ] [ 6.98754263]] b = [ 4.01742554] 上記の例では、 costとtrainという2つの新しい変数があります。 これらの2つの変数を使用して、トレーニングモデルで使用するオプティマイザーと最小化する関数を定義しました。
最後に、 Wとbの出力パラメーターは、 generate_test_values関数で定義されたものと同じである必要があります。 17行目では、 w1=2 、 w2=3 、 w3=7 、 b=4の場合にトレーニングする線形データポイントを生成するために使用する関数を実際に定義しました。 上記の例からの線形回帰は、複数の独立変数が使用される多変量です。
結論
このTensorFlowチュートリアルからわかるように、TensorFlowは、数式や多次元配列の操作を簡単にする強力なフレームワークです。これは、機械学習で基本的に必要なことです。 また、データグラフの実行とスケーリングの複雑さを抽象化します。
時間の経過とともにTensorFlowの人気が高まり、開発者は画像認識、ビデオ検出、感情分析などのテキスト処理などのディープラーニング手法を使用して問題を解決するために使用しています。他のライブラリと同様に、慣れるまでに時間がかかる場合があります。 TensorFlowが構築されている概念に。 また、ドキュメントとコミュニティサポートの助けを借りて、問題をデータグラフとして表現し、TensorFlowで解決することで、大規模な機械学習を面倒なプロセスから解放できます。
