Analiza expresiei în structura datelor: tipuri de notație, asociativitate și prioritate

Analiza este procesul de analiză a unui șir de simboluri, exprimate în limbaje naturale sau de calculator, care vor acorda gramatică formală . Analiza expresiei în structura datelor înseamnă evaluarea expresiilor aritmetice și logice. Mai întâi, să vedem cum este scrisă o expresie aritmetică:

• 9+9
• Cb

O expresie poate fi scrisă cu constante, variabile și simboluri care pot acționa ca operator sau paranteză. Toată această expresie trebuie să urmeze un set specific de reguli. Conform acestei reguli, parsarea expresiei se face pe baza gramaticii.

O expresie aritmetică este exprimată sub formă de notație . Acum, există trei moduri de a scrie o expresie în Aritmetică:

• Notație infixă
• Notație de prefix (poloneză).
• Notație postfix (invers-poloneză).

Cu toate acestea, atunci când expresia este scrisă, rezultatul expresiei dorite rămâne aceeași. Înainte de a începe cu tipurile de notație, să vedem ce sunt Asociativitatea și Precedența în analiza expresiei în Structura datelor.

Dacă sunteți începător și doriți să aflați mai multe despre știința datelor, consultați cursurile noastre de știință a datelor de la universități de top.

Citiți: Grafice în structura datelor

Asociativitatea

Înainte de a începe, trebuie să știți ce este proprietatea Asociativității; vă oferă regulile pentru a rearanja parantezele într-o expresie pentru a oferi dovezi valide. Aceasta înseamnă că o rearanjare a parantezei trebuie să dea aceeași valoare ca și ecuația părinte. Oferă o regulă valabilă pentru înlocuirea operatorilor.

Într-o expresie care conține doi sau mai mulți operatori, operația efectuată nu contează decât dacă succesiunea de operanzi nu este interschimbată. Dacă expresia este scrisă folosind paranteze și în infix, schimbarea poziției nu modifică valoarea.

Deoarece în limbile indo-europene, expresiile sunt citite de la stânga la dreapta, majoritatea operatorilor infixi sunt asociativi la stânga; operatorii sunt evaluați cu aceeași prioritate. Creșterea puterii este regula folosită în luarea în considerare a operatorilor infixi. Operatorii de prefix sunt în general asociativi la dreapta, iar operatorii de postfix sunt asociativi la stânga.

În unele limbi, operatorilor și operanzilor li se dau valoare egală, unde Asociativitatea nu este considerată explicând această secvență de limbaj. În timp ce în unele limbi, operatorii sunt non-asociativi, acest lucru face ca utilizarea expresiilor complexe să fie necesară pentru utilizarea parantezelor, ceea ce crește complexitatea pentru programatori.

Prioritate în structura datelor

Ordinea de prioritate înseamnă ce ordine trebuie să urmeze operatorii într-o declarație de expresii. Acesta este folosit în mod obișnuit în timpul lucrului cu Infix Notation.

În situația operandului <operator> <operand> <operator> între cei doi operatori, preferința de alocare a operatorului este destul de complicată. Prin urmare, regulile de precedență ale operatorului sunt respectate pentru calcul. De exemplu, aici, înmulțirea are o prioritate mai mare, iar ulterior se efectuează operația de adunare.

• Cea mai comună regulă, dar nu atât de evidentă, este că operația de înmulțire și împărțire trebuie efectuată înainte de adunare și scădere. În mod obișnuit, acestea sunt colectate în același mod, astfel încât se acordă o importanță egală pentru toți operatorii.
• Luând în considerare această operație într-un format logic, variația este văzută în „și” și „sau”. Multe limbi oferă o importanță egală, în cazul în care operațiunii „sau” i se acordă o prioritate mai mare. Unele limbi consideră înmulțirea sau „&”, „&” adunarea „sau” Precedența egală, unde majoritatea limbilor oferă operații aritmetice cu cea mai mare precedență.
• Supraîncărcarea este cauzată de lipsa alocării corecte a Precedenței. Multe limbi oferă negație (adevărat/fals) o precedență mai mare decât expresiile de algebră vectorială, în timp ce unele oferă o prioritate egală.

Citește și: Idei de proiecte de structură a datelor

Tipuri de notație

Acum să învățăm cum poziția operatorului decide tipul de notație.

1. Notație infixă

În notația Infix, operatorii sunt utilizați între operanzi. În timp ce citești o expresie, notația Infix este destul de ușoară pentru oameni. Dar este destul de consumator de timp și spațiu pentru a procesa un argument infix atunci când vine vorba de un algoritm de computer. De exemplu: p + q

<operanzi> <operatori> <operanzi>

Infix Notation are nevoie de informații suplimentare pentru a efectua evaluarea; regulile sunt construite în limbajul de expresie folosind operatorul Asociativitate , De exemplu: p * ( q + r ) / s

• Regulile de asociativitate sugerează că expresia trebuie efectuată de la stânga la dreapta, astfel încât înmulțirea cu p să se facă înainte de împărțirea lui q.
• În mod similar, regulile pentru Precedență sugerează că operația de înmulțire și împărțire este efectuată înainte ca operația de adunare și scădere să fie efectuată.

2. Notație de prefix

Aici se scrie primul operator, urmat de un operand. Este denumit și notație poloneză. De exemplu +pq

<operatori> <operanzi> <operanzi>

De exemplu: p * ( q + r ) / s

Evaluarea trebuie efectuată de la stânga la dreapta, iar parantezele nu modifică sau schimbă modelul ecuației. Aici, adunarea trebuie finalizată înainte de înmulțire, deoarece poziția „+” este la stânga lui „*”.

Aici, fiecare operator efectuează operații pe valori care sunt imediat la stânga acestora. De exemplu, „+” de mai sus folosește „q” și „r”. Putem rezuma paranteze pentru a face acest lucru evident:

((p (qr +) *) s /)

Astfel, „( )” ia în considerare și folosește cele două valori după imediat precedentul „p”, și rezultatul +. În mod similar, „/” folosește rezultatul expresiei înmulțirii și „s”.

3. Notație postfixă

Notația Postfix, în primul rând operandul, este scrisă, urmată de un operator. Este, de asemenea, numită Notație poloneză inversă, de exemplu, pq+

<operanzi> <operanzi> <operatori>

În ceea ce privește Postfix, la fel ca și operațiunea Prefix a expresiei este de la stânga la dreapta și „( )” nu este necesar. Aici, operatorii efectuează pe cele mai apropiate două valori din dreapta. În exemplul de mai jos, parantezele sunt adăugate inutil, pentru a clarifica faptul că nu există niciun impact asupra evaluării.

(/ (* p (+ qr) ) s)

Aici „evaluarea operatorului este de la stânga la dreapta” valorile operațiunii sunt în dreapta lor, iar dacă valorile în sine implică calcule, atunci există o schimbare în ordinea evaluării. Luând exemplul de mai sus, vezi că „/” este operatorul principal din stânga.

Așteaptă până la finalizarea operației de înmulțire. Și în primul rând, operația de înmulțire trebuie efectuată înainte de începerea calculului împărțirii (și din exemplul de mai sus, este clar că operația de adunare trebuie să fie finalizată înainte de operația de înmulțire).

Deoarece operatorii Postfix Notation folosesc valoarea din dreapta ei; orice valoare care implică calcule va avea calculul deja finalizat pe măsură ce ne deplasăm spre stânga. Deci, putem concluziona că calculul expresiei nu este la fel ca operația operatorului Prefix.

Pentru a evidenția toate cele trei notații, operanzii vin în aceeași ordine, iar operatorii trebuie mutați pentru a oferi semnificația corectă în timpul calculului. Acest lucru trebuie luat în considerare în special atunci când luăm în considerare operatorii asimetrici „-” și „/” pentru a clarifica pq este întotdeauna qr, cu excepția cazului în care au aceeași valoare; valorile sunt echivalente cu „pq -” sau „- pq”

P+q ≡ +pq ≡ pq+

De exemplu:

Infix- p * q + r / s

Prefix – pq * rs / +

Post fix – + * pq / rs

Mai întâi, pentru a efectua operația, înmulțiți p și q și apoi împărțiți r cu s și, în cele din urmă, adăugați rezultatele.

Mai jos tabelul scurt între cele trei notații,

Notație infixă	Notație poloneză	Notație de lustruire inversă
p+q	+pq	pq+
(p+q)*r	+*pq	pqr+*
p*(q+r)	*p+qr	pqr*++
p÷q+r÷s	+÷pq÷rs	pq÷rs÷+
(pq)*(rs)	*-pq-rs	pq-rs-*

Conversie între notații

*Pentru a oferi o perspectivă clară, parantezele sunt adăugate în expresie,

Infix	Postfix	Prefix
( (p * q) + (r / s) )	( (pq *) (rs /) +)	(+ (*) pq) (/ rs) )
((p * (q + r) ) / s)	( (p (qr +) *) s /)	(/ (* p (+ qr) ) s)
(p * (q + (r / s) ) )	(p (q (rs /) +) *)	(* p (+ q (/ rs) ) )

• Puteți începe conversia direct în formele între paranteze de către operatori din paranteză, de exemplu (m + n) sau (mn +) sau (+ mn). Acum repetați acest lucru în toți operatorii, eliminând parantezele nedorite.
• Acum folosiți acest truc prezentat mai sus pentru a converti și analiza arborii - arborii de analiza echivalent pentru fiecare nod sunt:

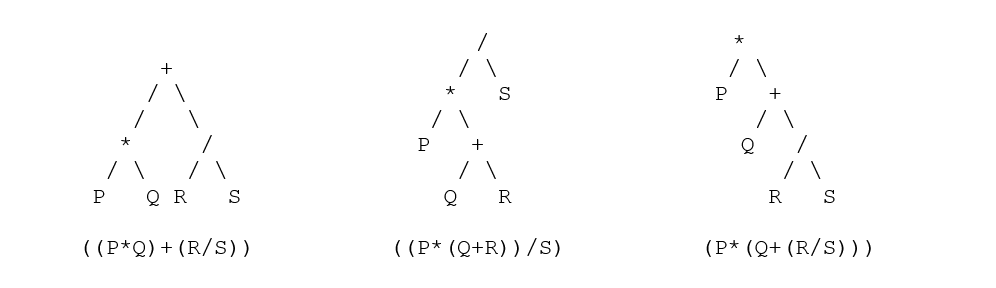
Checkout: Structura datelor și algoritmul în Python

Concluzie

Analiza expresiilor în Structura datelor , Notațiile Infix, Postfix și Prefix din expresiile aritmetice sunt destul de diferite, dar au aceleași moduri de scriere a expresiilor. Cunoașterea acestora este esențială în scrierea programelor.

Într-un limbaj de programare pentru computer, expresia este considerată și analizată din șir. Regula asociativității și precedenței se schimbă destul de mult în diferite limbi.

De ce să alegeți un curs de știință a datelor cu upGrad?

Știința datelor este unul dintre domeniile în plină expansiune în informatică. Companiile au nevoie de programatori care au o bună cunoaștere a elementelor de bază, ceea ce este fundamental pentru programare, indiferent de limbajul de codare.

upGrad se concentrează pe furnizarea de cursuri perspicace și informative, acoperind fiecare nevoie de bază pentru a deveni un om de știință a datelor. Programul PG executiv de 12 luni al upGrad în știința datelor. , oferit de IIIT Bangalore, este primul curs certificat NASSCOM din India, care vine cu mentorat personalizat 1:1 din partea experților din industria științei datelor, care acoperă toate limbajele de programare, instrumentele și bibliotecile esențiale. Vă oferă cea mai bună bază pentru a vă începe munca de știință a datelor bine plătită.

Ce sunt structurile de date?

Structurile de date sunt folosite pentru a organiza datele în memorie. Există mai multe metode de aranjare a datelor în memorie, inclusiv matrice, liste, stive, cozi și multe altele. Structura datelor nu este un limbaj de programare precum C, C++ sau Java. În schimb, este un set de tehnici care sunt folosite pentru a aranja datele în memorie în orice limbaj de programare. O structură de date este o metodă de organizare, manipulare și stocare eficientă a datelor. Elementele de date pot fi parcurse pur și simplu cu ajutorul structurii de date. Este esențial în îmbunătățirea vitezei unui program, deoarece sarcina principală a programului este să salveze și să recupereze datele utilizatorului cât mai repede posibil.

Care sunt utilizările reale ale analizării datelor?

Procesul de transformare a datelor dintr-un format în altul este cunoscut sub numele de analizare a datelor. Ele sunt utilizate pe scară largă în compilatoare pentru analizarea codului computerului și generarea codului mașină. Procesul de conversie a datelor dintr-un format în altul este cunoscut sub numele de analizare a datelor. Deoarece HTML brut pe care îl primim este greu de înțeles, analizatorii sunt adesea folosiți în scraping online. Solicităm ca datele să fie convertite într-un format care poate fi citit de om. Acest lucru ar putea implica crearea de rapoarte folosind șiruri HTML sau tabele pentru a oferi cele mai relevante informații.

Cum ajută Asociativitatea și Precedența în structurarea datelor?

Ordinea de evaluare a expresiilor este determinată de două proprietăți ale operatorilor: precedență și asociativitate. Precedența ajută la stabilirea modului în care trebuie grupați termenii dintr-o expresie și cum ar trebui evaluată o expresie. Deoarece majoritatea expresiilor folosesc cadrul BODMAS, anumiți operatori au prioritate față de alții. Când doi operatori au aceeași prioritate într-o expresie, se aplică regula asociativității. În funcție de preferința compilatorului, asociativitatea poate fi fie de la stânga la dreapta, fie de la dreapta la stânga.