Penguraian Ekspresi dalam Struktur Data: Jenis Notasi, Asosiatif & Prioritas

Parsing adalah proses menganalisis string simbol, dinyatakan dalam bahasa alami atau komputer yang sesuai dengan tata bahasa formal . Expression Parsing dalam Struktur Data berarti evaluasi ekspresi aritmatika dan logika. Pertama, mari kita lihat bagaimana ekspresi aritmatika ditulis:

• 9+9
• Cb

Ekspresi dapat ditulis dengan konstanta, variabel, dan simbol yang dapat bertindak sebagai operator atau tanda kurung. Semua ekspresi ini harus mengikuti seperangkat aturan tertentu. Menurut aturan ini, penguraian ekspresi dilakukan berdasarkan tata bahasa.

Ekspresi aritmatika dinyatakan dalam bentuk Notasi . Sekarang, ada tiga cara untuk menulis ekspresi dalam Aritmatika:

• Notasi Infiks
• Notasi Awalan (Polandia)
• Notasi Postfix (Polandia Terbalik)

Namun, ketika ekspresi ditulis, output dari ekspresi yang diinginkan tetap sama. Sebelum memulai dengan jenis Notasi, mari kita lihat apa itu Associativity dan Precedence dalam ekspresi Parsing dalam Struktur Data.

Jika Anda seorang pemula dan tertarik untuk mempelajari lebih lanjut tentang ilmu data, lihat kursus ilmu data kami dari universitas terkemuka.

Baca: Grafik dalam Struktur Data

Keterkaitan

Sebelum memulai, Anda perlu mengetahui apa itu properti Associativity; itu memberi Anda aturan untuk mengatur ulang tanda kurung dalam ekspresi untuk memberikan bukti yang valid. Ini berarti penataan ulang braket perlu memberikan nilai yang sama dengan persamaan induk. Ini memberikan aturan yang valid untuk mengganti operator.

Dalam ekspresi yang mengandung dua atau lebih operator, operasi yang dilakukan tidak menjadi masalah kecuali urutan operan tidak dipertukarkan. Jika ekspresi ditulis menggunakan tanda kurung dan dalam infiks, mengubah posisi tidak mengubah nilainya.

Karena dalam bahasa Indo-Eropa, ekspresi dibaca dari kiri ke kanan, sebagian besar operator infiks adalah asosiatif kiri; operator dievaluasi dalam prioritas yang sama. Naik kekuasaan adalah aturan yang digunakan dalam mempertimbangkan operator infiks. Operator prefiks umumnya asosiatif kanan, dan operator postfix asosiatif kiri.

Dalam beberapa bahasa, operator dan operan diberi nilai yang sama, di mana Associativity tidak dianggap membuat urutan bahasa ini menjadi eksplisit. Sementara dalam beberapa bahasa, operatornya non-asosiatif, ini membuat penggunaan ekspresi kompleks diperlukan untuk penggunaan tanda kurung, yang meningkatkan kerumitan bagi programmer.

Prioritas dalam Struktur Data

Urutan Prioritas berarti urutan apa yang harus diikuti oleh operator dalam pernyataan ekspresi. Ini biasanya digunakan saat bekerja dengan Notasi Infix.

Dalam situasi operan <operator> <operand> <operator> antara dua operator, preferensi untuk mengalokasikan operator cukup rumit. Oleh karena itu, aturan Precedence operator diikuti untuk perhitungan. Misalnya, Di sini, perkalian memiliki prioritas yang lebih tinggi, dan kemudian operasi penambahan dilakukan.

• Aturan yang paling umum tetapi tidak begitu jelas adalah bahwa operasi perkalian dan pembagian harus dilakukan sebelum penambahan dan pengurangan. Biasanya, mereka dikumpulkan dengan cara yang sama, sehingga sama pentingnya disediakan untuk semua operator.
• Mempertimbangkan operasi ini dalam format logis, variasi terlihat dalam "dan" dan "atau." Banyak bahasa memberikan kepentingan yang sama, di mana operasi "atau" diberikan Prioritas yang lebih tinggi. Beberapa bahasa menganggap perkalian atau "&," "&" penambahan "atau" Prioritas yang sama, di mana sebagian besar bahasa menyediakan operasi aritmatika dengan Prioritas tertinggi.
• Overloading disebabkan karena tidak ada alokasi Precedence yang tepat. Banyak bahasa memberikan negasi (benar/salah) Precedence lebih tinggi daripada ekspresi aljabar vektor, sementara beberapa memberikan Precedence yang sama.

Baca Juga: Ide Proyek Struktur Data

Jenis Notasi

Sekarang mari kita pelajari bagaimana posisi operator menentukan jenis Notasi.

1. Notasi Infiks

Dalam Notasi Infix, operator digunakan di antara operan. Saat membaca ekspresi, Notasi Infix cukup mudah bagi manusia. Tapi itu cukup memakan waktu dan ruang untuk memproses argumen infix ketika datang ke algoritma komputer. Misal: p + q

<operan> <operator> <operan>

Notasi Infix membutuhkan informasi tambahan untuk melakukan evaluasi; aturan dibangun ke dalam bahasa ekspresi menggunakan operator Associativity , Misalnya: p * ( q + r ) / s

• Aturan asosiatif menyarankan bahwa ekspresi perlu dilakukan dari kiri ke kanan, sehingga perkalian dengan p dilakukan sebelum pembagian q.
• Demikian pula, aturan untuk Prioritas menyarankan agar operasi perkalian dan pembagian dilakukan sebelum operasi penjumlahan dan pengurangan dilakukan.

2. Notasi Awalan

Di sini operator ditulis terlebih dahulu, diikuti oleh operan. Itu juga disebut sebagai Notasi Polandia. Misal +pq

<operator> <operan> <operan>

Misal: p * ( q + r ) / s

Evaluasi perlu dilakukan dari kiri ke kanan, dan tanda kurung tidak mengubah atau mengubah pola persamaan. Di sini, penjumlahan harus diselesaikan sebelum perkalian karena posisi “+” di kiri “*.”

Di sini, setiap operator melakukan operasi pada nilai yang berada tepat di sebelah kirinya. Misalnya, "+" di atas menggunakan "q" dan "r." Kami dapat meringkas tanda kurung untuk membuat ini terbuka:

((p (qr +) *) s /)

Jadi, "( )" mempertimbangkan dan menggunakan dua nilai setelah tepat sebelum "p", dan hasil dari +. Demikian pula, "/" menggunakan hasil dari ekspresi perkalian dan "s".

3. Notasi Postfix

Notasi Postfix, terutama operan, ditulis, diikuti oleh operator. Ini juga disebut sebagai Notasi Polandia Terbalik, misalnya, pq+

<operan> <operan> <operator>

Sedangkan untuk Postfix, sama dengan operasi Prefix dari ekspresi kiri-ke-kanan dan “( )” tidak diperlukan. Di sini, operator melakukan pada dua nilai terdekat dari kanan. Dalam contoh di bawah ini, tanda kurung tidak perlu ditambahkan, untuk memperjelas bahwa tidak ada dampak pada evaluasi.

(/ (* p (+ qr) ) s)

Di sini “evaluasi operator dari kiri ke kanan” nilai operasi berada di sebelah kanannya, dan jika nilai itu sendiri melibatkan perhitungan, maka ada perubahan dalam urutan evaluasi. Mengambil contoh yang tercantum di atas, lihat "/" adalah operator utama di sebelah kiri.

Itu menunggu sampai operasi perkalian selesai. Dan terutama, operasi perkalian perlu dilakukan sebelum perhitungan pembagian dimulai (dan dari contoh di atas, jelas bahwa operasi penjumlahan harus diselesaikan sebelum operasi perkalian).

Karena operator Notasi Postfix menggunakan nilai di sebelah kanannya; nilai apa pun yang melibatkan perhitungan akan memiliki perhitungan yang sudah selesai saat kita bergerak ke kiri. Jadi, kita dapat menyimpulkan bahwa perhitungan ekspresi tidak sama dengan operasi operator Prefix.

Untuk menyorot ketiga Notasi, operan datang dalam urutan yang sama, dan operator perlu dipindahkan untuk memberikan arti yang tepat selama perhitungan. Ini perlu dipertimbangkan terutama ketika mempertimbangkan operator asimetris "-" dan "/" untuk memperjelas pq adalah qr kecuali jika mereka memiliki nilai yang sama; nilainya setara dengan "pq -" atau "- pq"

P+q +pq pq+

Misalnya:

Infiks- p * q + r / s

Awalan – pq * rs / +

Perbaikan pos – + * pq / rs

Pertama, untuk melakukan operasi, kalikan p dan q dan kemudian bagi r dengan s dan, terakhir, tambahkan hasilnya.

Di bawah tabel singkat antara tiga Notasi,

Notasi Infiks	Notasi Polandia	Notasi pemoles terbalik
p+q	+ pq	pq+
(p+q)*r	+*pq	pqr+*
p*(q+r)	*p+qr	pqr*+ +
p÷q+r÷s	+÷pq÷rs	pq÷rs÷+
(pq)*(rs)	*-pq-rs	pq-rs-*

Konversi antar Notasi

*Untuk memberikan wawasan yang jelas, tanda kurung ditambahkan dalam ekspresi,

Infiks	Postfix	Awalan
( (p * q) + (r / s) )	( (pq *) (rs /) +)	(+ (* pq) (/ rs) )
((p * (q + r) ) / s)	( (p (qr +) *) s /)	(/ (* p (+ qr) ) s)
(p * (q + (r / s) ) )	(p (q (rs /) +) *)	(* p (+ q (/ rs) ) )

• Anda dapat mulai mengonversi secara langsung dalam bentuk kurung oleh operator dalam kurung, misalnya (m + n) atau (mn +) atau (+ mn). Sekarang ulangi ini di semua operator dengan menghapus tanda kurung yang tidak diinginkan.
• Sekarang gunakan trik yang ditunjukkan di atas untuk mengonversi dan mengurai pohon – pohon parse yang setara untuk setiap node adalah:

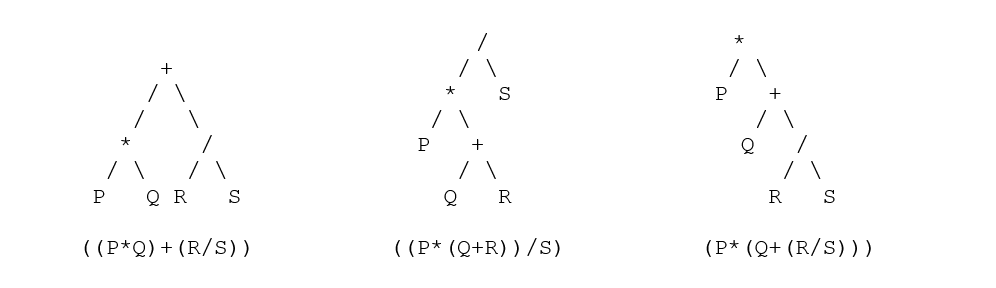
Checkout: Struktur & Algoritma Data dengan Python

Kesimpulan

Penguraian Ekspresi dalam Struktur Data , Infiks, Postfix, dan Awalan Notasi dalam ekspresi Aritmatika cukup berbeda tetapi memiliki cara penulisan ekspresi yang sama. Pengetahuan tentang ini sangat penting dalam menulis program.

Dalam bahasa pemrograman komputer, ekspresi dianggap dan diuraikan dari string. Aturan Associativity and Precedence cukup berubah dalam bahasa yang berbeda.

Mengapa memilih kursus Ilmu data dengan upGrad?

Ilmu data adalah salah satu bidang yang sedang booming dalam ilmu komputer. Perusahaan membutuhkan pemrogram yang memiliki pengetahuan dasar yang baik, yang merupakan dasar untuk pemrograman terlepas dari bahasa pengkodean.

upGrad berfokus pada penyediaan kelas yang berwawasan luas dan informatif, yang mencakup setiap kebutuhan dasar untuk menjadi ilmuwan data. Program PG Eksekutif 12-Bulan upGrad dalam Ilmu Data. , yang ditawarkan oleh IIIT Bangalore, adalah kursus bersertifikat NASSCOM pertama di India, yang dilengkapi dengan bimbingan pribadi 1:1 dari Pakar Industri Ilmu Data, yang mencakup semua Bahasa Pemrograman, Alat & Perpustakaan yang penting. Ini memberi Anda dasar terbaik untuk memulai pekerjaan ilmu data bergaji tinggi.

Apa itu Struktur Data?

Struktur data digunakan untuk mengatur data dalam memori. Ada beberapa metode untuk mengatur data di memori, antara lain array, list, stack, queue, dan masih banyak lagi yang lainnya. Struktur data bukanlah bahasa pemrograman seperti C, C++, atau Java. Sebaliknya, ini adalah seperangkat teknik yang digunakan untuk mengatur data dalam memori dalam bahasa pemrograman apa pun. Struktur data adalah metode untuk mengatur, menangani, dan menyimpan data secara efisien. Item data mungkin hanya dilalui dengan bantuan struktur data. Sangat penting dalam meningkatkan kecepatan program karena tugas utama program adalah menyimpan dan mengambil data pengguna secepat mungkin.

Apa kegunaan penguraian data di kehidupan nyata?

Proses transformasi data dari satu format ke format lain dikenal sebagai data parsing. Mereka banyak digunakan dalam kompiler untuk mengurai kode komputer dan menghasilkan kode mesin. Proses konversi data dari satu format ke format lain dikenal sebagai data parsing. Karena HTML mentah yang kami terima sulit dipahami, parser sering digunakan dalam pengikisan online. Kami membutuhkan data untuk diubah menjadi format yang dapat dibaca manusia. Ini mungkin menyiratkan pembuatan laporan menggunakan string atau tabel HTML untuk memberikan informasi yang paling relevan.

Bagaimana Associativity and Precedence membantu dalam penataan data?

Urutan evaluasi ekspresi ditentukan oleh dua properti operator: prioritas dan asosiatif. Prioritas membantu dalam menetapkan bagaimana istilah dalam ekspresi harus dikelompokkan dan bagaimana ekspresi harus dinilai. Karena sebagian besar ekspresi menggunakan kerangka kerja BODMAS, operator tertentu lebih diutamakan daripada yang lain. Ketika dua operator memiliki prioritas yang sama dalam sebuah ekspresi, aturan asosiatif diterapkan. Menurut preferensi kompiler, asosiatif dapat berupa kiri ke kanan atau kanan ke kiri.