Analyse d'expression dans la structure de données : types de notation, associativité et priorité

L'analyse syntaxique est le processus d'analyse d'une chaîne de symboles, exprimés dans des langages naturels ou informatiques qui conviendront à la grammaire formelle . L'analyse d'expressions dans la structure de données signifie l'évaluation d'expressions arithmétiques et logiques. Voyons d'abord comment s'écrit une expression arithmétique :

• 9+9
• Cb

Une expression peut être écrite avec des constantes, des variables et des symboles qui peuvent agir comme un opérateur ou une parenthèse. Toute cette expression doit suivre un ensemble de règles spécifiques. Selon cette règle, l'analyse de l'expression est effectuée sur la base de la grammaire.

Une expression arithmétique est exprimée sous la forme d'une notation . Maintenant, il y a trois façons d'écrire une expression en Arithmétique :

• Notation Infixe
• Notation du préfixe (polonais)
• Notation postfixée (polonais inversé)

Cependant, lorsque l'expression est écrite, la sortie de l'expression souhaitée reste la même. Avant de commencer avec les types de notation, voyons ce que sont l'associativité et la priorité dans l'analyse d'expression dans la structure de données.

Si vous êtes débutant et que vous souhaitez en savoir plus sur la science des données, consultez nos cours de science des données dispensés par les meilleures universités.

Lire : Graphiques dans la structure des données

Associativité

Avant de commencer, vous devez savoir ce qu'est la propriété d'associativité ; il vous fournit les règles pour réorganiser les parenthèses dans une expression afin de fournir une preuve valide. Cela signifie qu'un réarrangement de la parenthèse doit donner la même valeur que l'équation parente. Il fournit une règle valide pour remplacer les opérateurs.

Dans une expression contenant deux opérateurs ou plus, l'opération effectuée n'a pas d'importance à moins que la séquence d'opérandes ne soit pas interchangée. Si l'expression est écrite en utilisant les parenthèses et en infixe, changer la position ne change pas la valeur.

Parce que dans les langues indo-européennes, les expressions sont lues de gauche à droite, la plupart des opérateurs infixes sont associatifs à gauche ; les opérateurs sont évalués dans la même priorité. La montée en puissance est la règle utilisée pour considérer les opérateurs infixes. Les opérateurs préfixés sont généralement associatifs à droite et les opérateurs postfixés sont associatifs à gauche.

Dans certains langages, les opérateurs et les opérandes ont une valeur égale, où l'associativité n'est pas considérée comme rendant cette séquence de langage explicite. Alors que dans certains langages, les opérateurs sont non associatifs, cela rend l'utilisation d'expressions complexes nécessaire à l'utilisation de parenthèses, ce qui augmente la complexité pour les programmeurs.

Priorité dans la structure de données

L'ordre de priorité signifie quel ordre les opérateurs doivent suivre dans une déclaration d'expressions. Ceci est couramment utilisé lorsque vous travaillez avec Infix Notation.

Dans la situation de l' opérande <operator> <operand> <operator> entre les deux opérateurs, la préférence pour allouer l'opérateur est assez délicate. Par conséquent, les règles de priorité de l'opérateur sont suivies pour le calcul. Par exemple, ici, la multiplication a une priorité plus élevée, et plus tard l'opération d'addition est effectuée.

• La règle la plus courante mais pas si évidente est que l'opération de multiplication et de division doit être effectuée avant l'addition et la soustraction. En règle générale, ils sont collectés de la même manière, de sorte qu'une importance égale est accordée à tous les opérateurs.
• Considérant cette opération dans un format logique, la variation est visible dans "et" et "ou". De nombreuses langues offrent une importance égale, où l'opération "ou" a une priorité plus élevée. Certaines langues considèrent la multiplication ou "&", "&" l'addition "ou" la priorité égale, où la plupart des langues fournissent des opérations arithmétiques avec la priorité la plus élevée.
• La surcharge est due à une mauvaise allocation de priorité. De nombreux langages fournissent une priorité de négation (vrai/faux) supérieure à celle des expressions d'algèbre vectorielle, tandis que d'autres fournissent une priorité égale.

Lisez aussi : Idées de projets de structure de données

Types de notation

Voyons maintenant comment la position de l'opérateur décide du type de notation.

1. Notation Infixe

Dans Infix Notation, les opérateurs sont utilisés entre les opérandes. Lors de la lecture d'une expression, Infix Notation est assez facile pour les humains. Mais le traitement d'un argument infixe prend beaucoup de temps et d'espace lorsqu'il s'agit d'un algorithme informatique. Ex : p + q

<opérandes> <opérateurs> <opérandes>

Infix Notation a besoin d'informations supplémentaires pour effectuer l'évaluation ; les règles sont construites dans le langage d'expression à l'aide de l'opérateur Associativity , Par exemple : p * ( q + r ) / s

• Les règles d'associativité suggèrent que l'expression doit être effectuée de gauche à droite, de sorte que la multiplication par p soit effectuée avant la division de q.
• De même, les règles de priorité suggèrent que l'opération de multiplication et de division est effectuée avant l'opération d'addition et de soustraction.

2. Notation du préfixe

Ici, l'opérateur est écrit en premier, suivi d'un opérande. Il est également nommé notation polonaise. Par exemple +pq

<opérateurs> <opérandes> <opérandes>

Ex : p * ( q + r ) / s

L'évaluation doit être effectuée de gauche à droite, et les parenthèses n'altèrent ni ne changent le modèle d'équation. Ici, l'addition doit être terminée avant la multiplication car la position "+" est à gauche de "*".

Ici, chaque opérateur effectue des opérations sur des valeurs qui sont immédiatement à sa gauche. Par exemple, le « + » ci-dessus utilise le « q » et le « r ». Nous pouvons résumer les parenthèses pour rendre cela manifeste :

((p (qr +) *) s /)

Ainsi, le « ( ) » considère et utilise les deux valeurs immédiatement après « p », et le résultat du +. De même, le "/" utilise le résultat de l'expression de multiplication et le "s".

3. Notation postfixée

La notation postfixée, principalement l'opérande, est écrite, suivie d'un opérateur. Il est également nommé Notation polonaise inversée, par exemple, pq +

<opérandes> <opérandes> <opérateurs>

Comme pour Postfix, la même chose que l'opération Préfixe de l'expression est de gauche à droite et "( )" sont inutiles. Ici, les opérateurs agissent sur les deux valeurs les plus proches à partir de la droite. Dans l'exemple ci-dessous, des parenthèses sont ajoutées inutilement, pour préciser qu'il n'y a pas d'impact sur l'évaluation.

(/ (* p (+ qr) ) s)

Ici, "l'évaluation de l'opérateur est de gauche à droite", les valeurs d'opération sont à leur droite, et si les valeurs elles-mêmes impliquent des calculs, alors il y a un changement dans l'ordre d'évaluation. En prenant l'exemple ci-dessus, voir le "/" est l'opérateur principal sur la gauche.

Il attend que l'opération de multiplication soit terminée. Et principalement, l'opération de multiplication doit être effectuée avant le début du calcul de division (et d'après l'exemple ci-dessus, il est clair que l'opération d'addition doit être terminée avant l'opération de multiplication).

Parce que les opérateurs Postfix Notation utilisent la valeur à sa droite ; toutes les valeurs impliquant des calculs auront le calcul déjà terminé lorsque nous nous déplacerons vers la gauche. Ainsi, nous pouvons conclure que le calcul de l'expression n'est pas identique à l'opération de l'opérateur de préfixe.

Pour mettre en évidence les trois notations, les opérandes sont dans le même ordre et les opérateurs doivent être déplacés pour fournir la bonne signification lors du calcul. Cela doit être pris en compte en particulier lors de l'examen des opérateurs asymétriques "-" et "/" pour qu'il soit clair que pq est toujours qr à moins qu'ils n'aient la même valeur ; les valeurs sont équivalentes à "pq -" ou "- pq"

P+q ≡ +pq ≡ pq+

Par exemple:

Infixe- p * q + r / s

Préfixe – pq * rs / +

Après correction – + * pq / rs

Tout d'abord, pour effectuer l'opération, multipliez p et q, puis divisez r par s et, enfin, additionnez les résultats.

Ci-dessous des résumés de table entre les trois notations,

Notation Infixe	Notation polonaise	Notation polonaise inversée
p+q	+pq	pq+
(p+q)*r	+*pq	pqr+*
p*(q+r)	*p+qr	pqr*+ +
p÷q+r÷s	+÷pq÷rs	pq÷rs÷+
(pq)*(rs)	*-pq-rs	pq-rs-*

Conversion entre notations

*Pour fournir un aperçu clair, les crochets sont ajoutés dans l'expression,

Infixe	Suffixe	Préfixe
( (p * q) + (r / s) )	( (pq *) (rs /) +)	(+ (* pq) (/ rs) )
((p * (q + r) ) / s)	( (p (qr +) *) s /)	(/ (* p (+ qr) ) s)
(p * (q + (r / s) ) )	(p (q (rs /) +) *)	(* p (+ q (/ rs) ) )

• Vous pouvez commencer la conversion directement dans les formes entre parenthèses par des opérateurs entre parenthèses, par exemple (m + n) ou (mn +) ou (+ mn). Maintenant, répétez ceci dans tous les opérateurs en supprimant les parenthèses indésirables.
• Utilisez maintenant cette astuce montrée ci-dessus pour convertir et analyser les arbres - les arbres d'analyse équivalents pour chaque nœud sont :

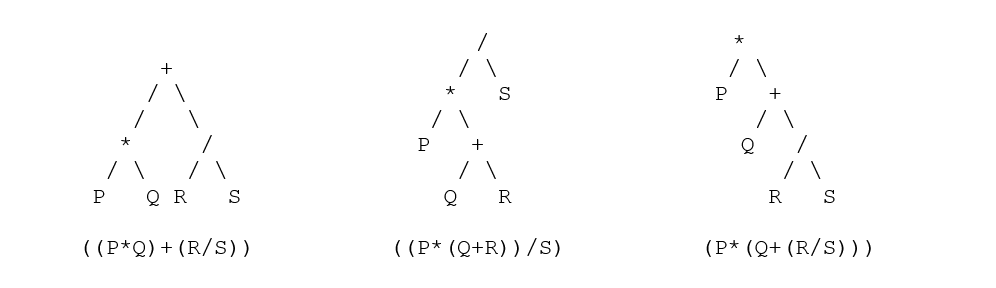
Checkout : structure de données et algorithme en Python

Conclusion

L'analyse d'expression dans la structure de données , l'infixe, le postfixe et les notations de préfixe dans les expressions arithmétiques sont assez différentes mais ont les mêmes façons d'écrire les expressions. La connaissance de ceux-ci est essentielle dans l'écriture de programmes.

Dans un langage de programmation informatique, l'expression est considérée et analysée à partir de la chaîne. La règle d'associativité et de priorité change assez dans différentes langues.

Pourquoi choisir une formation en Data science avec upGrad ?

La science des données est l'un des domaines en plein essor de l'informatique. Les entreprises ont besoin de programmeurs qui ont une bonne connaissance des bases, ce qui est fondamental pour programmer quel que soit le langage de codage.

upGrad se concentre sur la fourniture de cours perspicaces et informatifs, couvrant tous les besoins de base pour devenir un scientifique des données. Programme exécutif PG de 12 mois d'upGrad en science des données. , proposé par IIIT Bangalore, est le premier cours certifié NASSCOM en Inde, qui comprend un mentorat personnalisé 1: 1 d'experts de l'industrie de la science des données, couvrant tous les langages de programmation, outils et bibliothèques essentiels. Il vous fournit la meilleure base pour commencer votre travail bien rémunéré en science des données.

Que sont les Structures de Données ?

Les structures de données sont utilisées pour organiser les données en mémoire. Il existe plusieurs méthodes pour organiser les données en mémoire, notamment les tableaux, les listes, les piles, les files d'attente et bien d'autres. La structure de données n'est pas un langage de programmation comme le sont C, C++ ou Java. Au lieu de cela, il s'agit d'un ensemble de techniques utilisées pour organiser les données en mémoire dans n'importe quel langage de programmation. Une structure de données est une méthode d'organisation, de gestion et de stockage efficaces des données. Les éléments de données peuvent être simplement parcourus à l'aide d'une structure de données. Il est crucial pour améliorer la vitesse d'un programme puisque le travail principal du programme est de sauvegarder et de récupérer les données de l'utilisateur aussi rapidement que possible.

Quelles sont les utilisations réelles de l'analyse des données ?

Le processus de transformation des données d'un format à un autre est connu sous le nom d'analyse de données. Ils sont largement utilisés dans les compilateurs pour analyser le code informatique et générer du code machine. Le processus de conversion de données d'un format à un autre est appelé analyse de données. Étant donné que le code HTML brut que nous recevons est difficile à comprendre, les analyseurs sont souvent utilisés pour le grattage en ligne. Nous exigeons que les données soient converties dans un format lisible par l'homme. Cela peut impliquer la création de rapports à l'aide de chaînes ou de tableaux HTML pour fournir les informations les plus pertinentes.

Comment l'associativité et la priorité aident-elles à la structuration des données ?

L'ordre d'évaluation des expressions est déterminé par deux propriétés des opérateurs : priorité et associativité. La priorité aide à établir comment les termes d'une expression doivent être regroupés et comment une expression doit être évaluée. Étant donné que la plupart des expressions utilisent le framework BODMAS, certains opérateurs ont priorité sur d'autres. Lorsque deux opérateurs ont la même priorité dans une expression, la règle d'associativité est appliquée. Selon la préférence du compilateur, l'associativité peut être de gauche à droite ou de droite à gauche.