Análisis de expresiones en la estructura de datos: tipos de notación, asociatividad y precedencia

El análisis sintáctico es el proceso de analizar una cadena de símbolos, expresados ​​en lenguajes naturales o informáticos que concordarán con la gramática formal . El análisis de expresiones en la estructura de datos significa la evaluación de expresiones aritméticas y lógicas. Primero, veamos cómo se escribe una expresión aritmética:

• 9+9
• Cb

Una expresión se puede escribir con constantes, variables y símbolos que pueden actuar como un operador o paréntesis. Toda esta expresión necesita seguir un conjunto específico de reglas. De acuerdo con esta regla, el análisis de la expresión se realiza en función de la gramática.

Una expresión aritmética se expresa en forma de notación . Ahora, hay tres formas de escribir una expresión en Aritmética:

• Notación infija
• Notación de prefijo (polaco)
• Notación de sufijo (polaco inverso)

Sin embargo, cuando se escribe la expresión, la salida de la expresión deseada sigue siendo la misma. Antes de comenzar con los tipos de notación, veamos qué son la asociatividad y la precedencia en el análisis de expresiones en la estructura de datos.

Si es un principiante y está interesado en obtener más información sobre la ciencia de datos, consulte nuestros cursos de ciencia de datos de las mejores universidades.

Leer: Gráficos en estructura de datos

Asociatividad

Antes de comenzar, necesita saber qué es la propiedad de asociatividad; le proporciona las reglas para reorganizar los paréntesis en una expresión para proporcionar una prueba válida. Esto significa que una reorganización del corchete debe dar el mismo valor que la ecuación principal. Proporciona una regla válida para reemplazar a los operadores.

En una expresión que contiene dos o más operadores, la operación realizada no importa a menos que no se intercambie la secuencia de operandos. Si la expresión se escribe entre paréntesis y en infijo, cambiar la posición no cambia el valor.

Debido a que en los idiomas indoeuropeos, las expresiones se leen de izquierda a derecha, la mayoría de los operadores infijos son asociativos a la izquierda; los operadores se evalúan con la misma precedencia. Ascendente en potencia es la regla utilizada al considerar los operadores infijos. Los operadores de prefijo son generalmente asociativos por la derecha y los operadores de sufijo son asociativos por la izquierda.

En algunos lenguajes, los operadores y operandos tienen el mismo valor, donde la Asociatividad no se considera haciendo explícita esta secuencia de lenguaje. Si bien en algunos lenguajes los operadores no son asociativos, esto hace necesario el uso de expresiones complejas para el uso de corchetes, lo que aumenta la complejidad para los programadores.

Precedencia en la estructura de datos

Orden de precedencia significa qué orden deben seguir los operadores en una declaración de expresiones. Esto se usa comúnmente cuando se trabaja con notación infija.

En la situación de <operador> <operando> <operador> operando entre los dos operadores, la preferencia para asignar el operador es bastante complicada. Por lo tanto, se siguen las reglas de precedencia de operadores para el cálculo. Por ejemplo, aquí, la multiplicación tiene mayor prioridad, y luego se realiza la operación de suma.

• La regla más común pero no tan obvia es que la operación de multiplicación y división debe realizarse antes que la suma y la resta. Por lo general, se recopilan de la misma manera, por lo que se otorga la misma importancia a todos los operadores.
• Considerando esta operación en un formato lógico, se observa variación en “y” y “o”. Muchos idiomas brindan la misma importancia, donde la operación "o" tiene mayor precedencia. Algunos idiomas consideran la multiplicación o “&”, “&” suma “o” la Precedencia igual, donde la mayoría de los idiomas proporcionan operaciones aritméticas con la Precedencia más alta.
• La sobrecarga se debe a que no se ha asignado correctamente la precedencia. Muchos lenguajes proporcionan una prioridad de negación (verdadero/falso) más alta que las expresiones de álgebra vectorial, mientras que algunos proporcionan la misma precedencia.

Lea también: Ideas de proyectos de estructura de datos

Tipos de notación

Ahora aprendamos cómo la posición del operador decide el tipo de notación.

1. Notación de infijos

En notación infija, los operadores se utilizan entre los operandos. Al leer una expresión, la notación infija es bastante fácil para los humanos. Pero requiere mucho tiempo y espacio procesar un argumento infijo cuando se trata de un algoritmo informático. Por ejemplo: p + q

<operandos> <operadores> <operandos>

Infix Notation necesita información adicional para realizar la evaluación; las reglas se construyen en el lenguaje de expresión utilizando el operador Asociatividad , Por ejemplo: p * ( q + r ) / s

• Las reglas de asociatividad sugieren que la expresión debe realizarse de izquierda a derecha, de modo que la multiplicación por p se realice antes que la división por q.
• De manera similar, las reglas de precedencia sugieren que la operación de multiplicación y división se realiza antes de realizar la operación de suma y resta.

2. Notación de prefijo

Aquí el operador se escribe primero, seguido de un operando. También se denomina notación polaca. Por ejemplo, +pq

<operadores> <operandos> <operandos>

Por ejemplo: p * ( q + r ) / s

La evaluación debe realizarse de izquierda a derecha y los corchetes no alteran ni cambian el patrón de la ecuación. Aquí, la suma debe completarse antes que la multiplicación porque la posición "+" queda a la izquierda de "*".

Aquí, cada operador realiza operaciones en valores que están inmediatamente a la izquierda de ellos. Por ejemplo, el "+" de arriba usa la "q" y la "r". Podemos resumir corchetes para hacer esto manifiesto:

((p(qr+)*)s/)

Así, el “( )” considera y utiliza los dos valores inmediatamente posteriores a la “p”, y el resultado del +. De manera similar, la “/” usa el resultado de la expresión de multiplicación y la “s”.

3. Notación de sufijo

Se escribe la notación de sufijo, principalmente el operando, seguida de un operador. También se denomina notación polaca inversa, p. ej., pq+

<operandos> <operandos> <operadores>

En cuanto a Postfix, al igual que la operación Prefix de la expresión es de izquierda a derecha y "( )" son innecesarios. Aquí, los operadores actúan en los dos valores más cercanos desde la derecha. En el siguiente ejemplo, se agregan corchetes innecesariamente para aclarar que no hay impacto en la evaluación.

(/ (* p (+ qr) ) s)

Aquí, "la evaluación del operador es de izquierda a derecha", los valores de operación están a su derecha, y si los valores mismos involucran cálculos, entonces hay un cambio en el orden de evaluación. Tomando el ejemplo mencionado anteriormente, vea que "/" es el operador principal a la izquierda.

Espera hasta que se complete la operación de multiplicación. Y principalmente, la operación de multiplicación debe realizarse antes de que se inicie el cálculo de la división (y del ejemplo anterior, está claro que la operación de suma debe completarse antes de la operación de multiplicación).

Porque los operadores de notación Postfix usan el valor a su derecha; cualquier valor que involucre cálculos tendrá el cálculo ya completado a medida que nos movemos hacia la izquierda. Entonces, podemos concluir que el cálculo de la expresión no es lo mismo que la operación del operador Prefijo.

Para resaltar las tres notaciones, los operandos vienen en el mismo orden y es necesario mover los operadores para proporcionar el significado correcto durante el cálculo. Esto debe tenerse en cuenta especialmente cuando se consideran los operadores asimétricos "-" y "/" para dejar claro que pq siempre es qr a menos que tengan el mismo valor; los valores son equivalentes a “pq -” o “- pq”

P+q ≡ +pq ≡ pq+

P.ej:

Infijo- p * q + r / s

Prefijo – pq * rs / +

Corrección posterior – + * pq / rs

Primero, para realizar la operación, multiplica p y q y luego divide r entre s y, por último, suma los resultados.

Debajo de los resúmenes de la tabla entre las tres anotaciones,

Notación infija	Notación polaca	Notación de pulido inverso
p+q	+pq	pq+
(p+q)*r	+*pq	pqr+*
p*(q+r)	*p+qr	pq*+ +
p÷q+r÷s	+÷pq÷rs	pq÷rs÷+
(pq)*(rs)	*-pq-rs	pq-rs-*

Conversión entre notaciones

*Para proporcionar una idea clara, los corchetes se agregan en la expresión,

Infijo	Sufijo	Prefijo
( (p * q) + (r / s) )	((pq*) (rs/)+)	(+ (* pq) (/ rs) )
((p * (q + r) ) / s)	((p(qr+)*)s/)	(/ (* p (+ qr) ) s)
(p * (q + (r / s) ) )	(p(q(rs/)+)*)	(* pag (+ q (/ rs) ) )

• Puede comenzar a convertir directamente en las formas entre paréntesis mediante operadores en el paréntesis, por ejemplo (m + n) o (mn +) o (+ mn). Ahora repita esto en todos los operadores eliminando los corchetes no deseados.
• Ahora use este truco que se muestra arriba para convertir y analizar árboles: los árboles de análisis equivalentes para cada nodo son:

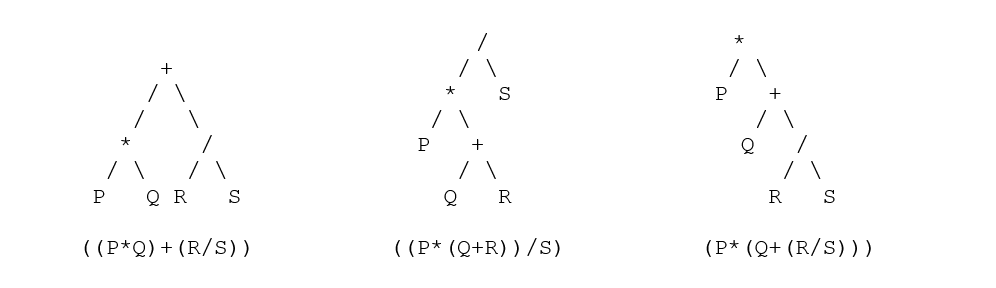
Pago: estructura de datos y algoritmo en Python

Conclusión

El análisis de expresiones en la estructura de datos , las notaciones de infijo, sufijo y prefijo en las expresiones aritméticas son bastante diferentes pero tienen las mismas formas de escribir expresiones. El conocimiento de estos es esencial en la escritura de programas.

En un lenguaje de programación de computadoras, la expresión se considera y se analiza a partir de la cadena. La regla de Asociatividad y Precedencia cambia bastante en diferentes idiomas.

¿Por qué elegir un curso de ciencia de datos con upGrad?

La ciencia de datos es uno de los campos en auge de la informática. Las empresas necesitan programadores que tengan un buen conocimiento de los conceptos básicos, lo cual es fundamental para programar independientemente del lenguaje de codificación.

upGrad se enfoca en brindar clases detalladas e informativas, cubriendo todas las necesidades básicas para convertirse en un científico de datos. Programa ejecutivo PG de 12 meses de upGrad en ciencia de datos. , ofrecido por IIIT Bangalore, es el primer curso certificado por NASSCOM de India, que viene con tutoría personalizada 1: 1 de expertos de la industria de ciencia de datos, que cubre todos los lenguajes, herramientas y bibliotecas de programación esenciales. Le brinda la mejor base para comenzar su trabajo de ciencia de datos bien remunerado.

¿Qué son las estructuras de datos?

Las estructuras de datos se utilizan para organizar los datos en la memoria. Existen varios métodos para organizar los datos en la memoria, incluidos arreglos, listas, pilas, colas y muchos otros. La estructura de datos no es un lenguaje de programación como lo son C, C++ o Java. En cambio, es un conjunto de técnicas que se utilizan para organizar datos en la memoria en cualquier lenguaje de programación. Una estructura de datos es un método para organizar, manejar y almacenar datos de manera eficiente. Los elementos de datos se pueden recorrer simplemente con la ayuda de la estructura de datos. Es crucial para mejorar la velocidad de un programa, ya que el trabajo principal del programa es guardar y recuperar los datos del usuario lo más rápido posible.

¿Cuáles son los usos reales del análisis de datos?

El proceso de transformación de datos de un formato a otro se conoce como análisis de datos. Se utilizan ampliamente en compiladores para analizar código de computadora y generar código de máquina. El proceso de convertir datos de un formato a otro se conoce como análisis de datos. Debido a que el HTML sin procesar que recibimos es difícil de entender, los analizadores se emplean a menudo en el raspado en línea. Requerimos que los datos se conviertan a un formato legible por humanos. Esto podría implicar la creación de informes utilizando cadenas o tablas HTML para proporcionar la información más relevante.

¿Cómo ayudan la asociatividad y la precedencia en la estructuración de datos?

El orden de evaluación de las expresiones está determinado por dos propiedades de los operadores: precedencia y asociatividad. La precedencia ayuda a establecer cómo deben agruparse los términos de una expresión y cómo debe evaluarse una expresión. Debido a que la mayoría de las expresiones usan el marco BODMAS, ciertos operadores tienen prioridad sobre otros. Cuando dos operadores tienen la misma precedencia en una expresión, se aplica la regla de asociatividad. Según la preferencia del compilador, la asociatividad puede ser de izquierda a derecha o de derecha a izquierda.