Comprender la entropía del árbol de decisión en el aprendizaje automático

El árbol de decisiones es una parte del aprendizaje automático supervisado en el que se explica la entrada para la que se encuentra la salida en los datos de entrenamiento. En los árboles de decisión, los datos se dividen varias veces según los parámetros dados. Sigue dividiendo los datos en subconjuntos más pequeños y, simultáneamente, el árbol se desarrolla de forma incremental. El árbol tiene dos entidades, que son nodos de decisión y nodos hoja.

Diferentes entidades del árbol de decisión

1. Nodo de decisión

Los nodos de decisión son aquellos en los que se dividen los datos. Suele tener dos o más ramas.

2. Nodos de hoja

Los nodos hoja representan los resultados, la clasificación o las decisiones del evento. Un árbol binario para "Elegibilidad para el concurso de belleza Miss India":

Tomemos un ejemplo de un árbol binario simple para entender los árboles de decisión. Consideremos que desea averiguar si una niña es elegible para un concurso de belleza como Miss India.

El nodo de decisión primero pregunta si la niña es residente de la India. En caso afirmativo, ¿tiene entre 18 y 25 años de edad? Si es así, ella es elegible, de lo contrario no. Si no, ¿tiene certificados válidos? Si es así, ella es elegible, de lo contrario no. Este era un simple tipo de problema de sí o no. Los árboles de decisión se clasifican en dos tipos principales:

Debe leer: Árbol de decisiones en IA

Clasificación del árbol de decisión

1. Árboles de clasificación

Los árboles de clasificación son del tipo simple sí o no. Es similar al ejemplo que hemos visto anteriormente, donde el resultado tenía variables como 'elegible' o 'no elegible'. La variable de decisión aquí es categórica.

2. Árboles de regresión

En los árboles de regresión, la variable de resultado o la decisión es continua, por ejemplo, una letra como ABC.

Ahora que conoce completamente el árbol de decisiones y su tipo, podemos profundizar en él. Los árboles de decisión se pueden construir usando muchos algoritmos; sin embargo, ID3 o Iterative Dichotomiser 3 Algorithm es el mejor. Aquí es donde la entropía del árbol de decisión entra en escena.

El algoritmo ID3 en cada iteración pasa por un atributo no utilizado del conjunto y calcula la entropía H(s) o la ganancia de información IG(s). Dado que estamos más interesados ​​en saber sobre la entropía del árbol de decisión en el artículo actual, primero comprendamos el término Entropía y simplifiquemos con un ejemplo.

Entropía: para un conjunto finito S, la entropía, también llamada entropía de Shannon, es la medida de la cantidad de aleatoriedad o incertidumbre en los datos. Se denota por H(S).

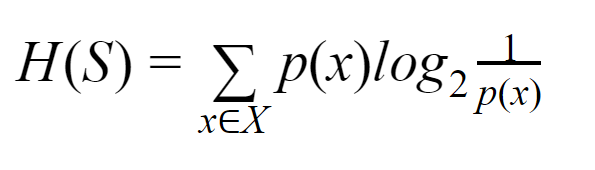
En términos simples, predice un determinado evento midiendo la pureza. El árbol de decisión se construye de arriba hacia abajo y comienza con un nodo raíz. Los datos de este nodo raíz se dividen o clasifican en subconjuntos que contienen instancias homogéneas.

Por ejemplo, considere un plato que se usa en los cafés que tiene escrito "estamos abiertos" en un lado y "estamos cerrados" en el otro lado. La probabilidad de "estamos abiertos" es 0,5 y la probabilidad de "estamos cerrados" es 0,5. Dado que no hay forma de determinar el resultado en este ejemplo particular, la entropía es la más alta posible.

Volviendo al mismo ejemplo, si la placa solo tuviera escrito "estamos abiertos" en ambos lados, entonces la entropía se puede predecir muy bien ya que sabemos que, ya sea quedándonos en el anverso o en el reverso, todavía vamos. tener "estamos abiertos". En otras palabras, no tiene aleatoriedad, lo que significa que la entropía es cero. Debe recordarse que cuanto menor sea el valor de la entropía, mayor será la pureza del evento, y cuanto mayor sea el valor de la entropía, menor será la pureza del evento.

Leer: Clasificación del árbol de decisión

Ejemplo

Consideremos que tienes 110 bolas. 89 de estas son bolas verdes y 21 son azules. Calcule la entropía para el conjunto de datos general.

Número total de bolas (n) = 110

Como tenemos 89 bolas verdes de 110, la probabilidad de que sean verdes sería del 80,91% o 89 dividido por 110, lo que da 0,8091. Además, la probabilidad de bola verde multiplicada por el logaritmo de la probabilidad de verde da 0,2473. Aquí, debe recordarse que un logaritmo de probabilidad siempre será un número negativo. Entonces, tenemos que adjuntar un signo negativo. Esto se puede expresar simplemente como:

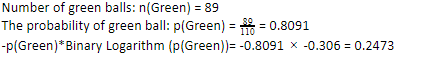
Ahora, realizando los mismos pasos para las bolas azules, tenemos 21 de 110. Por lo tanto, la probabilidad de una bola azul es 19,09% o 21 dividido por 110, lo que da 0,1909. Además, al multiplicar la probabilidad de las bolas azules por el logaritmo de la probabilidad de la bola azul, obtenemos 0,4561. Nuevamente, como se indicó anteriormente, agregaremos un signo negativo ya que el logaritmo de la probabilidad siempre da un resultado negativo, que no esperamos. Expresando esto simplemente:

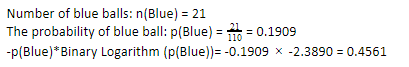
Ahora, la entropía del árbol de decisión de los datos generales viene dada por la suma de la entropía individual. Necesitamos la suma del producto de la probabilidad de la bola verde y el logaritmo de la probabilidad de la bola verde y el producto de la probabilidad de la bola azul y el logaritmo de la probabilidad de la bola azul.

Entropía (datos generales) = 0,2473 + 0,4561 = 0,7034

Este fue un ejemplo para ayudarlo a comprender cómo se calcula la entropía. Con suerte, es bastante claro, y usted tiene este concepto entendido. Calcular la entropía del árbol de decisión no es ciencia espacial como tal.

Sin embargo, debe estar atento al hacer los cálculos. Al estar en esta página, es obvio que usted es un entusiasta del aprendizaje automático y, por lo tanto, se espera que sepa cuán importante es el papel de cada detalle. Incluso el error más pequeño puede causar problemas y, por lo tanto, siempre debe tener los cálculos adecuados.

Pago: Tipos de árbol binario

Línea de fondo

Un árbol de decisión es aprendizaje automático supervisado que utiliza varios algoritmos para construir el árbol de decisión. Entre diferentes algoritmos, el algoritmo ID3 usa Entropía. La entropía no es sino la medida de la pureza del acontecimiento.

Sabemos que una carrera en aprendizaje automático tiene un futuro prometedor y una carrera floreciente. Esta industria todavía tiene un largo camino para alcanzar su punto máximo y, por lo tanto, las oportunidades para los entusiastas del aprendizaje automático están creciendo exponencialmente con muchas otras ventajas. Haga su lugar destacado en la industria del aprendizaje automático con la ayuda de los conocimientos y habilidades adecuados.

Si está interesado en obtener más información sobre el aprendizaje automático, consulte el Diploma PG en aprendizaje automático e IA de IIIT-B y upGrad, que está diseñado para profesionales que trabajan y ofrece más de 450 horas de capacitación rigurosa, más de 30 estudios de casos y asignaciones, IIIT- B Estado de exalumno, más de 5 proyectos prácticos finales prácticos y asistencia laboral con las mejores empresas.