Comprendre l'entropie de l'arbre de décision dans l'apprentissage automatique

L'arbre de décision fait partie de l'apprentissage automatique supervisé dans lequel vous expliquez l'entrée pour laquelle la sortie se trouve dans les données d'apprentissage. Dans les arbres de décision, les données sont divisées plusieurs fois en fonction des paramètres donnés. Il continue de diviser les données en sous-ensembles plus petits et, simultanément, l'arbre est développé de manière incrémentielle. L'arbre a deux entités, qui sont des nœuds de décision et des nœuds feuilles.

Différentes entités de l'arbre de décision

1. Nœud de décision

Les nœuds de décision sont ceux où les données se séparent. Il a généralement deux branches ou plus.

2. Nœuds feuilles

Les nœuds feuilles représentent les résultats, la classification ou les décisions de l'événement. Un arbre binaire pour "Eligibility for Miss India Beauty Pageant":

Prenons un exemple d'arbre binaire simple pour comprendre les arbres de décision. Considérons que vous voulez savoir si une fille est éligible pour un concours de beauté comme Miss India.

Le nœud de décision pose d'abord la question de savoir si la fille est résidente de l'Inde. Si oui, est-elle âgée de 18 à 25 ans ? Si oui, elle est éligible, sinon non. Si non, a-t-elle des certificats valides ? Si oui, elle est éligible, sinon non. C'était un simple type de problème oui ou non. Les arbres de décision sont classés en deux types principaux :

Doit lire : Arbre de décision dans l'IA

Classification de l'arbre de décision

1. Arbres de classement

Les arbres de classification sont des arbres simples de type oui ou non. Il est similaire à l'exemple que nous avons vu ci-dessus, où le résultat comportait des variables telles que "éligible" ou "non éligible". La variable de décision ici est catégorielle.

2. Arbres de régression

Dans les arbres de régression, la variable de résultat ou la décision est continue, par exemple, une lettre comme ABC.

Maintenant que vous connaissez parfaitement l'arbre de décision et son type, nous pouvons entrer dans les détails. Les arbres de décision peuvent être construits à l'aide de nombreux algorithmes ; cependant, ID3 ou Iterative Dichotomiser 3 Algorithm est le meilleur. C'est là que l'entropie de l'arbre de décision entre dans le cadre.

L'algorithme ID3 à chaque itération passe par un attribut inutilisé de l'ensemble et calcule l'entropie H(s) ou le gain d'information IG(s). Puisque nous sommes plus intéressés à en savoir plus sur l'entropie de l'arbre de décision dans l'article actuel, comprenons d'abord le terme Entropie et simplifions-le avec un exemple.

Entropie : pour un ensemble fini S, l'entropie, également appelée entropie de Shannon, est la mesure de la quantité d'aléatoire ou d'incertitude dans les données. Il est noté H(S).

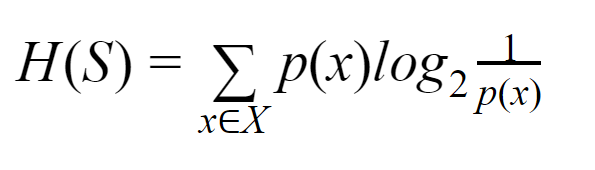
En termes simples, il prédit un certain événement en mesurant la pureté. L'arbre de décision est construit de manière descendante et commence par un nœud racine. Les données de ce nœud racine sont en outre partitionnées ou classées en sous-ensembles contenant des instances homogènes.

Par exemple, considérez une assiette utilisée dans les cafés avec "nous sommes ouverts" écrit d'un côté et "nous sommes fermés" de l'autre côté. La probabilité de "nous sommes ouverts" est de 0,5 et la probabilité de "nous sommes fermés" est de 0,5. Puisqu'il n'y a aucun moyen de déterminer le résultat dans cet exemple particulier, l'entropie est la plus élevée possible.

En revenant au même exemple, si la plaque n'avait que "nous sommes ouverts" écrit sur ses deux côtés, alors l'entropie peut être très bien prédite puisque nous savons déjà que soit en gardant le recto soit le verso, nous allons toujours avoir "nous sommes ouverts". En d'autres termes, il n'a pas de caractère aléatoire, ce qui signifie que l'entropie est nulle. Il convient de rappeler que plus la valeur de l'entropie est faible, plus la pureté de l'événement est élevée, et plus la valeur de l'entropie est élevée, plus la pureté de l'événement est faible.

Lire : Classification de l'arbre de décision

Exemple

Considérons que vous avez 110 balles. 89 d'entre elles sont des boules vertes et 21 sont bleues. Calculez l'entropie pour l'ensemble de données global.

Nombre total de boules (n) = 110

Puisque nous avons 89 boules vertes sur 110, la probabilité du vert serait de 80,91 % ou 89 divisé par 110, ce qui donne 0,8091. De plus, la probabilité de boule verte multipliée par le logarithme de la probabilité de vert donne 0,2473. Ici, il faut se rappeler qu'un logarithme de probabilité sera toujours un nombre négatif. Donc, nous devons attacher un signe négatif. Cela peut être exprimé simplement comme suit :

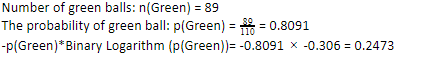
Maintenant, en effectuant les mêmes étapes pour les boules bleues, nous avons 21 sur 110. Par conséquent, la probabilité d'une boule bleue est de 19,09 % ou 21 divisé par 110, ce qui donne 0,1909. De plus, en multipliant la probabilité des boules bleues par le logarithme de la probabilité de la boule bleue, nous obtenons 0,4561. Encore une fois, comme indiqué ci-dessus, nous allons attacher un signe négatif puisque le logarithme de la probabilité donne toujours un résultat négatif, auquel nous ne nous attendons pas. En exprimant cela simplement :

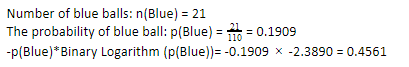
Maintenant, l' entropie de l'arbre de décision des données globales est donnée par la somme de l'entropie individuelle. Nous avons besoin de la somme du produit de la probabilité de boule verte et du log de la probabilité de boule verte et du produit de la probabilité de boule bleue et du log de la probabilité de boule bleue.

Entropie (données globales) = 0,2473 + 0,4561 = 0,7034

C'était un exemple pour vous aider à comprendre comment l'entropie est calculée. J'espère que c'est assez clair et que vous avez compris ce concept. Le calcul de l' entropie de l'arbre de décision n'est pas sorcier en tant que tel.

Cependant, vous devez être vif tout en faisant les calculs. Étant sur cette page, il est évident que vous êtes un passionné d'apprentissage automatique et, par conséquent, vous devez savoir à quel point le rôle de chaque détail est important. Même la plus petite erreur peut causer des problèmes, et par conséquent, vous devriez toujours avoir des calculs appropriés.

Paiement : Types d'arbre binaire

Conclusion

Un arbre de décision est un apprentissage automatique supervisé qui utilise divers algorithmes pour construire l'arbre de décision. Parmi différents algorithmes, l'algorithme ID3 utilise l'entropie. L'entropie n'est rien d'autre que la mesure de la pureté de l'événement.

Nous savons qu'une carrière dans l'apprentissage automatique a un avenir prometteur et une carrière florissante. Cette industrie a encore un long chemin à parcourir pour atteindre son apogée et, par conséquent, les opportunités pour les passionnés d'apprentissage automatique connaissent une croissance exponentielle avec de nombreux autres avantages. Faites votre place remarquable dans l'industrie de l'apprentissage automatique avec l'aide des bonnes connaissances et compétences.

Si vous souhaitez en savoir plus sur l'apprentissage automatique, consultez le diplôme PG en apprentissage automatique et IA de IIIT-B & upGrad, conçu pour les professionnels en activité et offrant plus de 450 heures de formation rigoureuse, plus de 30 études de cas et missions, IIIT- Statut B Alumni, plus de 5 projets de synthèse pratiques et aide à l'emploi avec les meilleures entreprises.