理解機器學習中的決策樹熵

決策樹是監督機器學習的一部分，您可以在其中解釋輸出在訓練數據中的輸入。 在決策樹中，數據根據給定的參數被分割多次。 它不斷地將數據分解成更小的子集，同時，樹也在逐步發展。 樹有兩個實體，分別是決策節點和葉節點。

決策樹的不同實體

1.決策節點

決策節點是數據拆分的節點。 它通常有兩個或多個分支。

2. 葉節點

葉節點代表事件的結果、分類或決策。 “印度小姐選美資格”的二叉樹：

讓我們以一個簡單的二叉樹為例來理解決策樹。 讓我們考慮一下，您想知道一個女孩是否有資格參加像印度小姐這樣的選美比賽。

決策節點首先詢問女孩是否是印度居民。 如果是，她的年齡在 18 至 25 歲之間嗎？ 如果是，她有資格，​​否則沒有。 如果沒有，她有有效的證件嗎？ 如果是，她有資格，​​否則沒有。 這是一個簡單的是或否類型的問題。 決策樹分為兩種主要類型：

必讀：人工智能中的決策樹

決策樹分類

1.分類樹

分類樹是簡單的是或否類型的樹。 它類似於我們在上面看到的示例，其中結果具有“合格”或“不合格”等變量。 這裡的決策變量是分類的。

2.回歸樹

在回歸樹中，結果變量或決策是連續的，例如像 ABC 這樣的字母。

現在您已經完全了解決策樹及其類型，我們可以深入了解它。 決策樹可以使用多種算法構建； 但是，ID3 或 Iterative Dichotomiser 3 算法是最好的一種。 這就是決策樹熵進入框架的地方。

每次迭代的 ID3 算法都會遍歷集合中未使用的屬性併計算熵 H(s) 或信息增益 IG(s)。 由於我們在當前文章中對了解決策樹熵更感興趣，因此讓我們首先了解熵這個術語並通過一個示例對其進行簡化。

熵：對於有限集 S，熵，也稱為香農熵，是數據中隨機性或不確定性的量度。 它用 H(S) 表示。

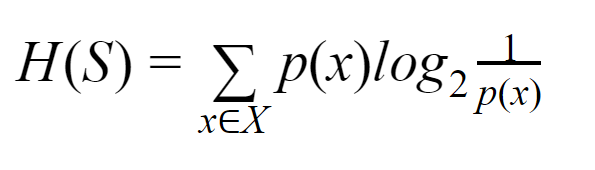
簡單來說，它通過測量純度來預測某個事件。 決策樹以自上而下的方式構建，從根節點開始。 該根節點的數據被進一步劃分或分類為包含同質實例的子集。

例如，考慮一個用於咖啡館的盤子，一面寫著“我們營業”，另一面寫著“我們關門”。 “我們是開放的”的概率是 0.5，“我們是封閉的”的概率是 0.5。 由於在此特定示例中無法確定結果，因此熵是可能的最高值。

再來看同一個例子，如果盤子的兩面都寫著“we are open”，那麼熵可以很好地預測，因為我們已經知道，要么保持正面，要么保持背面，我們仍在繼續有“我們是開放的”。 換句話說，它沒有隨機性，這意味著熵為零。 需要記住的是，熵值越低，事件的純度越高，熵值越高，事件的純度越低。

閱讀：決策樹分類

例子

讓我們考慮一下您有 110 個球。 其中89個是綠球，21個是藍球。 計算整個數據集的熵。

球總數 (n) = 110

由於我們在 110 個中有 89 個綠色球，綠色的概率是 80.91% 或 89 除以 110，得到 0.8091。 此外，綠色球的概率乘以綠色概率的對數得到 0.2473。 在這裡，應該記住，概率的對數始終是負數。 所以，我們必須附加一個負號。 這可以簡單地表示為：

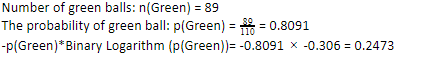
現在，對藍色球執行相同的步驟，110 個中有 21 個。因此，藍色球的概率是 19.09% 或 21 除以 110，得到 0.1909。 此外，將藍球的概率乘以藍球概率的對數，我們得到 0.4561。 同樣，如上所述，我們將附加一個負號，因為概率的對數總是給出負結果，這是我們沒有預料到的。 簡單地表達這一點：

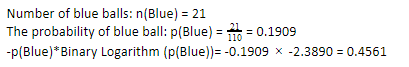
現在，整體數據的決策樹熵y 由單個熵的總和給出。 我們需要綠球概率與綠球概率對數的乘積和藍球概率與藍球概率對數的乘積之和。

熵（整體數據）= 0.2473 + 0.4561 =0.7034

這是幫助您了解如何計算熵的一個示例。 希望它很清楚，並且您已經理解了這個概念。 計算決策樹熵本身並不是火箭科學。

但是，在進行計算時，您必須敏銳。 在這個頁面上，很明顯你是一個機器學習愛好者，因此，你應該知道每一個細節的作用是多麼重要。 即使是最小的錯誤也會造成麻煩，因此，您應該始終進行適當的計算。

結帳：二叉樹的類型

底線

決策樹是有監督的機器學習，它使用各種算法來構建決策樹。 在不同的算法中，ID3 算法使用熵。 熵只不過是事件純度的量度。

我們知道，機器學習的職業前景廣闊，事業蒸蒸日上。 這個行業要達到頂峰還有很長的路要走，因此機器學習愛好者的機會正呈指數級增長，並具有許多其他優勢。 借助正確的知識和技能，讓您在機器學習行業中脫穎而出。

如果您有興趣了解有關機器學習的更多信息，請查看 IIIT-B 和 upGrad 的機器學習和人工智能 PG 文憑，該文憑專為工作專業人士設計，提供 450 多個小時的嚴格培訓、30 多個案例研究和作業、IIIT- B 校友身份、5 個以上實用的實踐頂點項目和頂級公司的工作協助。