Понимание энтропии дерева решений в машинном обучении

Дерево решений — это часть контролируемого машинного обучения, в которой вы объясняете входные данные, для которых выходные данные находятся в обучающих данных. В деревьях решений данные разбиваются несколько раз в соответствии с заданными параметрами. Он продолжает разбивать данные на более мелкие подмножества, и одновременно дерево развивается постепенно. Дерево состоит из двух объектов, которые являются узлами решений и конечными узлами.

Различные сущности дерева решений

1. Узел принятия решения

Узлы принятия решений — это те, где данные разбиваются. Обычно имеет две и более ветвей.

2. Листовые узлы

Листовые узлы представляют результаты, классификацию или решения события. Бинарное дерево для «Право на участие в конкурсе красоты Мисс Индия»:

Давайте возьмем пример простого бинарного дерева, чтобы понять деревья решений. Давайте представим, что вы хотите узнать, подходит ли девушка для участия в конкурсе красоты, таком как Мисс Индия.

Узел решения сначала задает вопрос, является ли девушка жительницей Индии. Если да, то ее возраст от 18 до 25 лет? Если да, то она имеет право, иначе нет. Если нет, есть ли у нее действительные сертификаты? Если да, то она имеет право, иначе нет. Это была простая проблема типа «да» или «нет». Деревья решений делятся на два основных типа:

Обязательно к прочтению: Дерево решений в ИИ

Классификация дерева решений

1. Деревья классификации

Деревья классификации представляют собой простые деревья типа «да» или «нет». Это похоже на пример, который мы видели выше, где результат имел такие переменные, как «приемлемо» или «не соответствует». Переменная решения здесь является категориальной.

2. Деревья регрессии

В деревьях регрессии переменная результата или решение являются непрерывными, например, буква типа ABC.

Теперь, когда вы полностью осведомлены о дереве решений и его типе, мы можем углубиться в его суть. Деревья решений могут быть построены с использованием многих алгоритмов; тем не менее, ID3 или алгоритм Iterative Dichotomiser 3 является лучшим. Здесь на помощь приходит энтропия дерева решений .

Алгоритм ID3 на каждой итерации просматривает неиспользуемый атрибут набора и вычисляет энтропию H(s) или IG(s) прироста информации. Поскольку нас больше интересует энтропия дерева решений в текущей статье, давайте сначала разберемся с термином энтропия и упростим его на примере.

Энтропия: для конечного множества S энтропия, также называемая энтропией Шеннона, является мерой степени случайности или неопределенности в данных. Обозначается H(S).

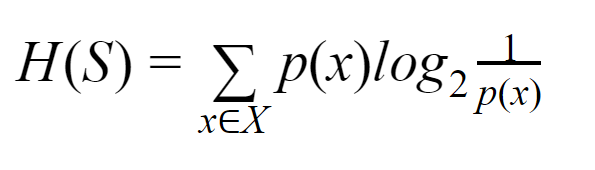
Проще говоря, он предсказывает определенное событие, измеряя чистоту. Дерево решений строится сверху вниз и начинается с корневого узла. Данные этого корневого узла дополнительно разбиваются или классифицируются на подмножества, содержащие однородные экземпляры.

Например, рассмотрим табличку, используемую в кафе, на которой с одной стороны написано «мы открыты», а с другой — «мы закрыты». Вероятность «мы открыты» равна 0,5, а вероятность «мы закрыты» равна 0,5. Поскольку в этом конкретном примере нет способа определить результат, энтропия является максимально возможной.

Возвращаясь к тому же примеру, если бы на обеих сторонах тарелки было написано только «мы открыты», то энтропию можно было бы предсказать очень хорошо, поскольку мы уже знаем, что, оставаясь на лицевой или обратной стороне, мы все равно движемся вперед. иметь «мы открыты». Другими словами, в нем нет случайности, то есть энтропия равна нулю. Следует помнить, что чем ниже значение энтропии, тем выше чистота события, а чем выше значение энтропии, тем ниже чистота события.

Читайте: Классификация дерева решений

Пример

Предположим, что у вас есть 110 шаров. Из них 89 зеленых шаров, а 21 синий. Вычислите энтропию для всего набора данных.

Общее количество мячей (n) = 110

Поскольку у нас есть 89 зеленых шаров из 110, вероятность того, что они будут зелеными, составит 80,91% или 89, деленное на 110, что дает 0,8091. Далее вероятность зеленого шара, умноженная на логарифм вероятности зеленого, дает 0,2473. Здесь следует помнить, что логарифм вероятности всегда будет отрицательным числом. Итак, мы должны поставить отрицательный знак. Это может быть выражено просто как:

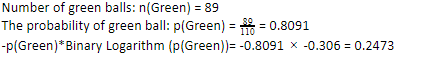
Теперь, выполняя те же действия для синих шаров, мы имеем 21 из 110. Следовательно, вероятность синего шара составляет 19,09% или 21, деленное на 110, что дает 0,1909. Далее, умножая вероятность синих шаров на логарифм вероятности синих шаров, получаем 0,4561. Опять же, как указано выше, мы будем добавлять отрицательный знак, поскольку журнал вероятности всегда дает отрицательный результат, которого мы не ожидаем. Выражая это просто:

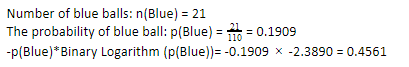
Теперь энтропия дерева решений y общих данных определяется как сумма индивидуальной энтропии. Нам нужна сумма произведения вероятности зеленого шара и логарифма вероятности зеленого шара и произведения вероятности синего шара и логарифма вероятности синего шара.

Энтропия (общие данные) = 0,2473 + 0,4561 = 0,7034.

Это был один пример, который поможет вам понять, как рассчитывается энтропия. Надеюсь, это довольно ясно, и вы поняли эту концепцию. Вычисление энтропии дерева решений не является ракетостроением как таковым.

Тем не менее, вы должны быть внимательны при выполнении расчетов. Находясь на этой странице, очевидно, что вы являетесь энтузиастом машинного обучения, и, следовательно, вы должны знать, насколько важна роль каждой мельчайшей детали. Даже малейшая ошибка может вызвать проблемы, а значит, у вас всегда должны быть правильные расчеты.

Оформить заказ: типы бинарного дерева

Нижняя линия

Дерево решений — это контролируемое машинное обучение, которое использует различные алгоритмы для построения дерева решений. Среди различных алгоритмов алгоритм ID3 использует энтропию. Энтропия есть не что иное, как мера чистоты события.

Мы знаем, что карьера в области машинного обучения имеет многообещающее будущее и процветающую карьеру. Этой отрасли еще предстоит пройти долгий путь, чтобы достичь своего пика, и, следовательно, возможности для энтузиастов машинного обучения растут в геометрической прогрессии вместе с множеством других преимуществ. Займите свое достойное место в индустрии машинного обучения с помощью правильных знаний и навыков.

Если вам интересно узнать больше о машинном обучении, ознакомьтесь с дипломом PG IIIT-B и upGrad в области машинного обучения и искусственного интеллекта, который предназначен для работающих профессионалов и предлагает более 450 часов тщательного обучения, более 30 тематических исследований и заданий, IIIT- Статус B Alumni, более 5 практических практических проектов и помощь в трудоустройстве в ведущих фирмах.