Makine Öğreniminde Karar Ağacı Entropisini Anlamak

Karar Ağacı, eğitim verilerinde çıktının olduğu girdiyi açıkladığınız Denetimli Makine Öğreniminin bir parçasıdır. Karar ağaçlarında, veriler verilen parametrelere göre birden çok kez bölünür. Verileri daha küçük alt kümelere ayırmaya devam eder ve aynı anda ağaç aşamalı olarak geliştirilir. Ağacın karar düğümleri ve yaprak düğümleri olmak üzere iki varlığı vardır.

Karar Ağacının Farklı Varlıkları

1. Karar Düğümü

Karar düğümleri, verilerin bölündüğü düğümlerdir. Genellikle iki veya daha fazla şubesi vardır.

2. Yaprak Düğümleri

Yaprak düğümler, olayın sonuçlarını, sınıflandırmasını veya kararlarını temsil eder. “Miss India Güzellik Yarışması için Uygunluk” için bir ikili ağaç:

Karar ağaçlarını anlamak için basit bir ikili ağaç örneğini ele alalım. Bir kızın Miss India gibi bir güzellik yarışmasına katılmaya uygun olup olmadığını öğrenmek istediğinizi düşünelim.

Karar düğümü önce kızın Hindistan'da ikamet edip etmediği sorusunu sorar. Evet ise, yaşı 18 ila 25 arasında mı? Evet ise, o uygun, yoksa değil. Hayır ise, geçerli sertifikaları var mı? Evet ise, o uygun, yoksa değil. Bu basit bir evet veya hayır sorunuydu. Karar ağaçları iki ana tipe ayrılır:

Okumalısınız: Yapay Zekada Karar Ağacı

Karar Ağacı Sınıflandırması

1. Sınıflandırma Ağaçları

Sınıflandırma ağaçları, basit evet veya hayır tipi ağaçlardır. Yukarıda gördüğümüz, sonucun 'uygun' veya 'uygun değil' gibi değişkenlere sahip olduğu örneğe benzer. Buradaki karar değişkeni Kategorik'tir.

2. Regresyon Ağaçları

Regresyon ağaçlarında, sonuç değişkeni veya karar süreklidir, örneğin ABC gibi bir harf.

Artık karar ağacının ve türünün tamamen farkında olduğunuza göre, onun derinliklerine inebiliriz. Karar ağaçları birçok algoritma kullanılarak oluşturulabilir; ancak ID3 veya Iterative Dichotomiser 3 Algoritması en iyisidir. Karar ağacı entropisinin çerçeveye girdiği yer burasıdır.

Her yinelemede ID3 algoritması, kümenin kullanılmayan bir özniteliğinden geçer ve Entropi H(ler)ini veya Bilgi Kazancı IG(ler)ini hesaplar. Bu makalede karar ağacı entropisi hakkında daha fazla bilgi edinmekle daha çok ilgilendiğimiz için, önce Entropi terimini anlayalım ve bir örnekle basitleştirelim.

Entropi: Sonlu bir S kümesi için, Shannon Entropisi olarak da adlandırılan Entropi, verilerdeki rastgelelik veya belirsizlik miktarının ölçüsüdür. H(S) ile gösterilir.

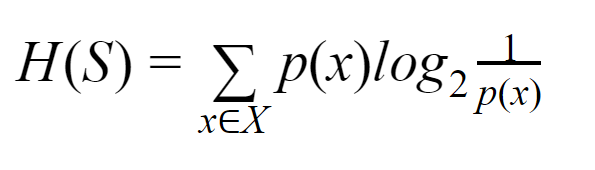
Basit bir ifadeyle, saflığı ölçerek belirli bir olayı tahmin eder. Karar ağacı yukarıdan aşağıya inşa edilir ve bir kök düğümle başlar. Bu kök düğümün verileri ayrıca homojen örnekler içeren alt kümelere bölünür veya sınıflandırılır.

Örneğin, kafelerde kullanılan ve bir tarafında “biz açığız” diğer tarafında “kapalıyız” yazan bir levhayı ele alalım. "Açığız" olasılığı 0,5'tir ve "kapalıyız" olasılığı 0,5'tir. Bu özel örnekte sonucu belirlemenin bir yolu olmadığından, entropi mümkün olan en yüksek değerdir.

Aynı örneğe gelecek olursak, eğer plakanın her iki tarafında sadece “biz açığız” yazılı olsaydı, o zaman entropi çok iyi tahmin edilebilir çünkü zaten bildiğimiz için ya önde ya da arkada kalırsak, hala devam ediyoruz. "biz açığız" olmak. Başka bir deyişle, rastgeleliği yoktur, yani entropi sıfırdır. Unutulmamalıdır ki entropi değeri ne kadar düşükse olayın saflığı o kadar yüksek ve entropi değeri ne kadar yüksekse olayın saflığı o kadar düşük olur.

Okuyun: Karar Ağacı Sınıflandırması

Örnek vermek

110 topunuz olduğunu düşünelim. Bunlardan 89'u yeşil, 21'i mavidir. Genel veri kümesi için entropiyi hesaplayın.

Toplam top sayısı (n) = 110

110'dan 89 yeşil topumuz olduğundan, yeşil olma olasılığı %80.91 veya 89 bölü 110 olur, bu da 0.8091 verir. Ayrıca, yeşil top olasılığının yeşil olasılığının logu ile çarpımı 0,2473'ü verir. Burada, bir olasılık günlüğünün her zaman negatif bir sayı olacağı unutulmamalıdır. Yani, negatif bir işaret eklemeliyiz. Bu basitçe şu şekilde ifade edilebilir:

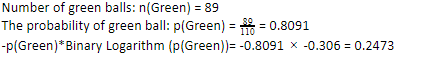
Şimdi, mavi toplar için aynı adımları uygulayarak, 110 üzerinden 21'imiz var. Dolayısıyla, mavi bir topun olasılığı %19,09 veya 21'in 110'a bölümüdür, bu da 0,1909 verir. Ayrıca, mavi topların olasılığını mavi topun olasılığının logu ile çarptığımızda 0.4561 elde ederiz. Yine, yukarıda belirtildiği gibi, olasılığın günlüğü her zaman beklemediğimiz olumsuz bir sonuç verdiği için olumsuz bir işaret ekleyeceğiz. Bunu basitçe ifade etmek:

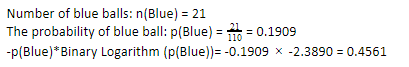
Şimdi, genel verilerin Karar Ağacı Entropisi , bireysel entropinin toplamı ile verilmektedir. Yeşil top olasılığının çarpımı ile yeşil top olasılığının logu ve mavi top olasılığının çarpımı ile mavi top olasılığının logunun toplamına ihtiyacımız var.

Entropi (Genel Veri)= 0.2473 + 0.4561 =0.7034

Bu, entropinin nasıl hesaplandığını anlamanıza yardımcı olacak bir örnekti. Umarım, oldukça açıktır ve bu kavramı anladınız. Karar ağacı entropisini hesaplamak roket bilimi değildir.

Ancak hesaplamaları yaparken dikkatli olmalısınız. Bu sayfada olmak, bir makine öğrenimi meraklısı olduğunuz açıktır ve bu nedenle, her bir detayın rolünün ne kadar önemli olduğunu bilmeniz beklenir. En küçük hata bile sorun çıkarabilir ve bu nedenle her zaman doğru hesaplamalara sahip olmalısınız.

Ödeme: İkili Ağaç Türleri

Sonuç olarak

Karar ağacı, karar ağacını oluşturmak için çeşitli algoritmalar kullanan denetimli makine öğrenimidir. Farklı algoritmalar arasında, ID3 algoritması Entropi kullanır. Entropi, olayın saflığının ölçüsünden başka bir şey değildir.

Makine öğrenimindeki bir kariyerin umut verici bir geleceğe ve gelişen bir kariyere sahip olduğunu biliyoruz. Bu endüstrinin zirveye ulaşması için daha uzun bir yolu var ve bu nedenle makine öğrenimi meraklıları için fırsatlar, birçok başka avantajla birlikte katlanarak büyüyor. Doğru bilgi ve becerilerin yardımıyla makine öğrenimi endüstrisinde dikkat çekici yerinizi alın.

Makine öğrenimi hakkında daha fazla bilgi edinmek istiyorsanız, çalışan profesyoneller için tasarlanmış ve 450+ saat zorlu eğitim, 30'dan fazla vaka çalışması ve ödev, IIIT- sunan IIIT-B & upGrad'ın Makine Öğrenimi ve Yapay Zeka PG Diplomasına göz atın. B Mezun statüsü, 5+ pratik uygulamalı bitirme projesi ve en iyi firmalarla iş yardımı.