理解机器学习中的决策树熵

决策树是监督机器学习的一部分，您可以在其中解释输出在训练数据中的输入。 在决策树中，数据根据给定的参数被分割多次。 它不断地将数据分解成更小的子集，同时，树也在逐步发展。 树有两个实体，分别是决策节点和叶节点。

决策树的不同实体

1.决策节点

决策节点是数据拆分的节点。 它通常有两个或多个分支。

2. 叶节点

叶节点代表事件的结果、分类或决策。 “印度小姐选美资格”的二叉树：

让我们以一个简单的二叉树为例来理解决策树。 让我们考虑一下，您想知道一个女孩是否有资格参加像印度小姐这样的选美比赛。

决策节点首先询问女孩是否是印度居民。 如果是，她的年龄在 18 至 25 岁之间吗？ 如果是，她有资格，否则没有。 如果没有，她有有效的证件吗？ 如果是，她有资格，否则没有。 这是一个简单的是或否类型的问题。 决策树分为两种主要类型：

必读：人工智能中的决策树

决策树分类

1.分类树

分类树是简单的是或否类型的树。 它类似于我们在上面看到的示例，其中结果具有“合格”或“不合格”等变量。 这里的决策变量是分类的。

2.回归树

在回归树中，结果变量或决策是连续的，例如像 ABC 这样的字母。

现在您已经完全了解决策树及其类型，我们可以深入了解它。 决策树可以使用多种算法构建； 但是，ID3 或 Iterative Dichotomiser 3 算法是最好的一种。 这就是决策树熵进入框架的地方。

每次迭代的 ID3 算法都会遍历集合中未使用的属性并计算熵 H(s) 或信息增益 IG(s)。 由于我们在当前文章中对了解决策树熵更感兴趣，因此让我们首先了解熵这个术语并通过一个示例对其进行简化。

熵：对于有限集 S，熵，也称为香农熵，是数据中随机性或不确定性的量度。 它用 H(S) 表示。

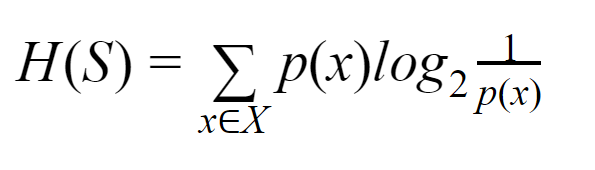
简单来说，它通过测量纯度来预测某个事件。 决策树以自上而下的方式构建，从根节点开始。 该根节点的数据被进一步划分或分类为包含同质实例的子集。

例如，考虑一个用于咖啡馆的盘子，一面写着“我们营业”，另一面写着“我们关门”。 “我们是开放的”的概率是 0.5，“我们是封闭的”的概率是 0.5。 由于在此特定示例中无法确定结果，因此熵是可能的最高值。

再来看同一个例子，如果盘子的两面都写着“我们是开放的”，那么熵可以很好地预测，因为我们已经知道要么保持正面要么保持背面，我们仍在继续有“我们是开放的”。 换句话说，它没有随机性，这意味着熵为零。 需要记住的是，熵值越低，事件的纯度越高，熵值越高，事件的纯度越低。

阅读：决策树分类

例子

让我们考虑一下您有 110 个球。 其中89个是绿球，21个是蓝球。 计算整个数据集的熵。

球总数 (n) = 110

由于我们在 110 个中有 89 个绿色球，绿色的概率是 80.91% 或 89 除以 110，得到 0.8091。 此外，绿色球的概率乘以绿色概率的对数得到 0.2473。 在这里，应该记住，概率的对数始终是负数。 所以，我们必须附加一个负号。 这可以简单地表示为：

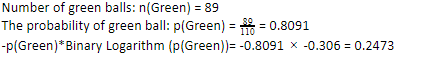
现在，对蓝色球执行相同的步骤，110 个中有 21 个。因此，蓝色球的概率是 19.09% 或 21 除以 110，得到 0.1909。 此外，将蓝球的概率乘以蓝球概率的对数，我们得到 0.4561。 同样，如上所述，我们将附加一个负号，因为概率的对数总是给出负结果，这是我们没有预料到的。 简单地表达这一点：

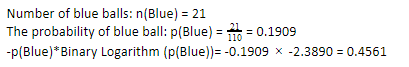
现在，整体数据的决策树熵y 由单个熵的总和给出。 我们需要绿球概率与绿球概率对数的乘积和蓝球概率与蓝球概率对数的乘积之和。

熵（整体数据）= 0.2473 + 0.4561 =0.7034

这是帮助您了解如何计算熵的一个示例。 希望它很清楚，并且您已经理解了这个概念。 计算决策树熵本身并不是火箭科学。

但是，在进行计算时，您必须敏锐。 在这个页面上，很明显你是一个机器学习爱好者，因此，你应该知道每一个细节的作用是多么重要。 即使是最小的错误也会造成麻烦，因此，您应该始终进行适当的计算。

结帐：二叉树的类型

底线

决策树是有监督的机器学习，它使用各种算法来构建决策树。 在不同的算法中，ID3 算法使用熵。 熵只不过是事件纯度的量度。

我们知道，机器学习的职业前景广阔，事业蒸蒸日上。 这个行业要达到顶峰还有很长的路要走，因此机器学习爱好者的机会正呈指数级增长，并具有许多其他优势。 借助正确的知识和技能，让您在机器学习行业中脱颖而出。

如果您有兴趣了解有关机器学习的更多信息，请查看 IIIT-B 和 upGrad 的机器学习和人工智能 PG 文凭，该文凭专为工作专业人士设计，提供 450 多个小时的严格培训、30 多个案例研究和作业、IIIT- B 校友身份、5 个以上实用的实践顶点项目和顶级公司的工作协助。