Ausdrucksanalyse in der Datenstruktur: Notationsarten, Assoziativität und Vorrang

Parsing ist der Prozess der Analyse einer Reihe von Symbolen, die in natürlichen oder Computersprachen ausgedrückt werden, die einer formalen Grammatik entsprechen . Ausdrucksanalyse in der Datenstruktur bedeutet die Auswertung von arithmetischen und logischen Ausdrücken. Sehen wir uns zunächst an, wie ein arithmetischer Ausdruck geschrieben wird:

• 9+9
• Kb

Ein Ausdruck kann mit Konstanten, Variablen und Symbolen geschrieben werden, die als Operator oder Klammer fungieren können. All diese Ausdrücke müssen einem bestimmten Satz von Regeln folgen. Gemäß dieser Regel erfolgt die Analyse des Ausdrucks auf der Grundlage der Grammatik.

Ein arithmetischer Ausdruck wird in Form von Notation ausgedrückt . Nun gibt es drei Möglichkeiten, einen Ausdruck in Arithmetik zu schreiben:

• Infix-Notation
• Präfix (polnische) Notation
• Postfix (umgekehrt polnische) Notation

Wenn der Ausdruck jedoch geschrieben wird, bleibt die Ausgabe des gewünschten Ausdrucks gleich. Bevor wir mit den Notationstypen beginnen, sehen wir uns an, was Assoziativität und Vorrang bei der Analyse von Ausdrücken in der Datenstruktur sind.

Wenn Sie Anfänger sind und mehr über Data Science erfahren möchten, sehen Sie sich unsere Data Science-Kurse von Top-Universitäten an.

Lesen Sie: Graphen in der Datenstruktur

Assoziativität

Bevor Sie beginnen, müssen Sie wissen, was Assoziativitätseigenschaft ist; Es bietet Ihnen die Regeln zum Neuanordnen von Klammern in einem Ausdruck, um einen gültigen Beweis zu liefern. Dies bedeutet, dass eine Neuanordnung der Klammer den gleichen Wert wie die übergeordnete Gleichung ergeben muss. Es stellt eine gültige Regel zum Ersetzen der Operatoren bereit.

In einem Ausdruck, der zwei oder mehr Operatoren enthält, spielt die ausgeführte Operation keine Rolle, es sei denn, die Reihenfolge der Operanden ist nicht vertauscht. Wenn der Ausdruck mit Klammern und Infix geschrieben wird, ändert eine Änderung der Position nicht den Wert.

Da in indogermanischen Sprachen Ausdrücke von links nach rechts gelesen werden, sind die meisten Infix-Operatoren linksassoziativ; Operatoren werden mit der gleichen Priorität ausgewertet. Steigende Macht ist die Regel, die bei der Betrachtung der Infix-Operatoren verwendet wird. Präfixoperatoren sind im Allgemeinen rechtsassoziativ und Postfixoperatoren sind linksassoziativ.

In einigen Sprachen werden Operatoren und Operanden gleich bewertet, wobei die Assoziativität nicht berücksichtigt wird, was diese Sprachsequenz explizit macht. Während in einigen Sprachen die Operatoren nicht assoziativ sind, macht dies die Verwendung komplexer Ausdrücke für die Verwendung von Klammern erforderlich, was die Komplexität für Programmierer erhöht.

Vorrang in der Datenstruktur

Rangfolge bedeutet, welche Reihenfolge die Operatoren in einer Anweisung von Ausdrücken einhalten müssen. Dies wird häufig bei der Arbeit mit Infix-Notation verwendet.

In der Situation von <Operator> <Operand> <Operator> Operand zwischen den beiden Operatoren ist die Präferenz für die Zuweisung des Operators ziemlich schwierig. Daher werden die Operatorvorrangregeln für die Berechnung befolgt. Beispielsweise hat hier die Multiplikation einen höheren Vorrang, und später wird die Additionsoperation durchgeführt.

• Die häufigste, aber nicht so offensichtliche Regel ist, dass Multiplikations- und Divisionsoperationen vor Addition und Subtraktion durchgeführt werden müssen. In der Regel werden sie auf die gleiche Weise erfasst, sodass allen Operatoren die gleiche Bedeutung beigemessen wird.
• Betrachtet man diese Operation in einem logischen Format, sieht man Variationen in „und“ und „oder“. Viele Sprachen sind gleich wichtig, wobei der „oder“-Operation eine höhere Priorität eingeräumt wird. Einige Sprachen betrachten Multiplikation oder „&“, „&“ Addition „oder“ die gleiche Priorität, wobei die meisten Sprachen arithmetische Operationen mit der höchsten Priorität bereitstellen.
• Eine Überlastung wird aufgrund einer nicht ordnungsgemäßen Zuordnung der Priorität verursacht. Viele Sprachen bieten der Negation (wahr/falsch) eine höhere Priorität als Ausdrücke der Vektoralgebra, während einige die gleiche Priorität haben.

Lesen Sie auch: Ideen für Datenstrukturprojekte

Arten der Notation

Lassen Sie uns nun lernen, wie die Operatorposition die Art der Notation bestimmt.

1. Infix-Notation

In der Infix-Notation werden Operatoren zwischen den Operanden verwendet. Beim Lesen eines Ausdrucks ist die Infix-Notation für Menschen recht einfach. Aber es ist ziemlich zeit- und platzaufwändig, ein Infix-Argument zu verarbeiten, wenn es um einen Computeralgorithmus geht. Bsp.: p + q

<Operanden> <Operatoren> <Operanden>

Infix Notation benötigt zusätzliche Informationen, um die Auswertung durchzuführen; Regeln werden mithilfe der Operatoren Assoziativität , Zum Beispiel: p * ( q + r ) / s

• Assoziativitätsregeln legen nahe, dass der Ausdruck von links nach rechts ausgeführt werden muss, sodass die Multiplikation mit p vor der Division von q erfolgt.
• In ähnlicher Weise schlagen Regeln für Vorrang vor, dass Multiplikations- und Divisionsoperationen durchgeführt werden, bevor Additions- und Subtraktionsoperationen durchgeführt werden.

2. Präfixnotation

Hier steht zuerst der Operator, gefolgt von einem Operanden. Es wird auch als polnische Notation bezeichnet. zB +pq

<Operatoren> <Operanden> <Operanden>

Beispiel: p * ( q + r ) / s

Die Auswertung muss von links nach rechts erfolgen, und Klammern ändern oder ändern das Gleichungsmuster nicht. Hier muss die Addition vor der Multiplikation abgeschlossen werden, da die Position „+“ links von „*“ steht.

Hier führt jeder Operator Operationen an Werten durch, die unmittelbar links davon stehen. Zum Beispiel verwendet das „+“ oben das „q“ und „r“. Wir können Klammern zusammenfassen, um dies offenzulegen:

((p (qr +) *) s /)

Daher berücksichtigt und verwendet „( )“ die beiden Werte nach dem unmittelbar vorangehenden „p“ und das Ergebnis von +. Ebenso verwendet das „/“ das Ergebnis des Multiplikationsausdrucks und das „s“.

3. Postfix-Notation

In Postfix-Notation wird hauptsächlich der Operand geschrieben, gefolgt von einem Operator. Sie wird auch als umgekehrte polnische Notation bezeichnet, zB pq+

<Operanden> <Operanden> <Operatoren>

Was Postfix betrifft, so ist die Präfix-Operation des Ausdrucks von links nach rechts und „( )“ sind unnötig. Hier arbeiten Operatoren an den zwei nächsten Werten von rechts. Im folgenden Beispiel werden unnötigerweise Klammern hinzugefügt, um zu verdeutlichen, dass dies keinen Einfluss auf die Bewertung hat.

(/ (* p (+ qr) ) s)

Hier sind „Operatorauswertung von links nach rechts“ Operationswerte rechts davon, und wenn die Werte selbst Berechnungen beinhalten, dann gibt es eine Änderung in der Auswertungsreihenfolge. Im oben aufgeführten Beispiel sehen Sie, dass „/“ der primäre Operator auf der linken Seite ist.

Es wartet, bis die Multiplikationsoperation abgeschlossen ist. Und in erster Linie muss die Multiplikationsoperation durchgeführt werden, bevor die Divisionsberechnung gestartet wird (und aus dem obigen Beispiel ist klar, dass die Additionsoperation vor der Multiplikationsoperation abgeschlossen werden muss).

Da Postfix-Notationsoperatoren den Wert rechts davon verwenden; Alle Werte, die Berechnungen beinhalten, haben die Berechnung bereits abgeschlossen, wenn wir uns nach links bewegen. Wir können also schlussfolgern, dass die Ausdrucksberechnung nicht dasselbe ist wie die Operation des Präfix-Operators.

Um alle drei Notationen hervorzuheben, kommen die Operanden in der gleichen Reihenfolge, und Operatoren müssen verschoben werden, um während der Berechnung die richtige Bedeutung zu liefern. Dies muss besonders berücksichtigt werden, wenn die asymmetrischen Operatoren „-“ und „/“ betrachtet werden, um klarzustellen, dass pq immer qr ist, es sei denn, sie haben denselben Wert; die Werte entsprechen „pq -“ oder „- pq“

P+q ≡ +pq ≡ pq+

Z.B:

Infix- p * q + r / s

Präfix – pq * rs / +

Postfix – + * pq / rs

Um die Operation durchzuführen, multiplizieren Sie zunächst p und q und teilen Sie später r durch s und addieren Sie schließlich die Ergebnisse.

Unterhalb der Tabelle kurz zwischen den drei Notationen,

Infix-Notation	Polnische Notation	Umgekehrte polnische Notation
p+q	+pq	pq+
(p+q)*r	+*pq	pqr+*
p*(q+r)	*p+qr	pqr*+ +
p÷q+r÷s	+÷pq÷rs	pq÷rs÷+
(pq)*(rs)	*-pq-rs	pq-rs-*

Konvertierung zwischen Notationen

*Um einen klaren Einblick zu ermöglichen, werden die Klammern in den Ausdruck eingefügt,

Infix	Postfix	Präfix
( (p * q) + (r / s) )	( (pq *) (rs /) +)	(+ (* pq) (/ rs) )
((p * (q + r) ) / s)	( (p (qr +) *) s /)	(/ (* p (+ qr) ) s)
(p * (q + (r / s) ) )	(p (q (rs /) +) *)	(* p (+ q (/rs) ) )

• Durch Operatoren in der Klammer, zB (m + n) oder (mn +) oder (+ mn), können Sie in den Klammerformen direkt mit der Umrechnung beginnen. Wiederholen Sie dies nun in allen Operatoren, indem Sie die unerwünschten Klammern entfernen.
• Verwenden Sie nun diesen oben gezeigten Trick, um Bäume zu konvertieren und zu analysieren – die entsprechenden Analysebäume für jeden Knoten sind:

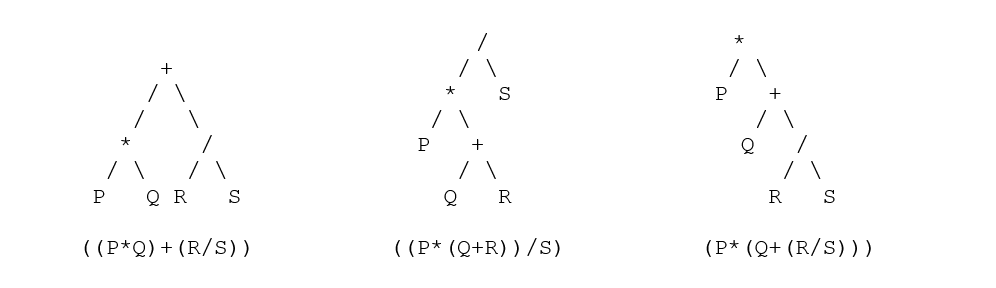
Kasse: Datenstruktur und Algorithmus in Python

Fazit

Ausdrucksanalyse in Datenstrukturen , Infix-, Postfix- und Präfixnotationen in arithmetischen Ausdrücken sind ziemlich unterschiedlich, haben aber die gleiche Art, Ausdrücke zu schreiben. Die Kenntnis dieser ist beim Schreiben von Programmen unerlässlich.

In einer Computerprogrammiersprache wird der Ausdruck betrachtet und aus der Zeichenkette geparst. Die Assoziativitäts- und Vorrangregel ändert sich in verschiedenen Sprachen ziemlich.

Warum einen Data-Science-Kurs mit upGrad wählen?

Data Science ist eines der boomenden Gebiete der Informatik. Unternehmen brauchen Programmierer, die über gute Grundlagenkenntnisse verfügen, die für die Programmierung unabhängig von der Programmiersprache von grundlegender Bedeutung sind.

upGrad konzentriert sich darauf, aufschlussreiche und informative Kurse anzubieten, die alle Grundbedürfnisse abdecken, um ein Datenwissenschaftler zu werden. Das 12-monatige Executive PG-Programm von upGrad in Data Science. , angeboten von IIIT Bangalore, ist Indiens erster NASSCOM-zertifizierter Kurs, der mit einer persönlichen 1:1-Betreuung durch Data-Science-Branchenexperten ausgestattet ist und alle wesentlichen Programmiersprachen, Tools und Bibliotheken abdeckt. Es bietet Ihnen die beste Grundlage, um Ihren hochbezahlten Data-Science-Job zu starten.

Was sind Datenstrukturen?

Datenstrukturen werden verwendet, um Daten im Speicher zu organisieren. Es gibt mehrere Methoden zum Anordnen von Daten im Speicher, darunter Arrays, Listen, Stapel, Warteschlangen und viele andere. Die Datenstruktur ist keine Programmiersprache wie C, C++ oder Java. Stattdessen handelt es sich um eine Reihe von Techniken, die verwendet werden, um Daten im Speicher in jeder Programmiersprache anzuordnen. Eine Datenstruktur ist eine Methode zum effizienten Organisieren, Handhaben und Speichern von Daten. Die Datenelemente können einfach mit Hilfe der Datenstruktur durchlaufen werden. Es ist entscheidend, die Geschwindigkeit eines Programms zu verbessern, da die Hauptaufgabe des Programms darin besteht, die Daten des Benutzers so schnell wie möglich zu speichern und abzurufen.

Was sind die realen Anwendungen der Datenanalyse?

Der Vorgang des Transformierens von Daten von einem Format in ein anderes wird als Datenparsing bezeichnet. Sie werden häufig in Compilern zum Analysieren von Computercode und zum Generieren von Maschinencode verwendet. Der Vorgang des Konvertierens von Daten von einem Format in ein anderes wird als Datenparsing bezeichnet. Da das unverarbeitete HTML, das wir erhalten, schwer zu verstehen ist, werden beim Online-Scraping häufig Parser eingesetzt. Wir verlangen, dass die Daten in ein für Menschen lesbares Format konvertiert werden. Dies kann das Erstellen von Berichten unter Verwendung von HTML-Strings oder -Tabellen beinhalten, um die relevantesten Informationen bereitzustellen.

Wie helfen Assoziativität und Vorrang bei der Datenstrukturierung?

Die Auswertungsreihenfolge von Ausdrücken wird durch zwei Eigenschaften von Operatoren bestimmt: Vorrang und Assoziativität. Der Vorrang hilft bei der Festlegung, wie Begriffe in einem Ausdruck gruppiert und wie ein Ausdruck bewertet werden sollte. Da die meisten Ausdrücke das BODMAS-Framework verwenden, haben bestimmte Operatoren Vorrang vor anderen. Wenn zwei Operatoren in einem Ausdruck denselben Vorrang haben, wird die Regel der Assoziativität angewendet. Je nach Präferenz des Compilers kann die Assoziativität entweder von links nach rechts oder von rechts nach links erfolgen.