تحليل التعبير في بنية البيانات: أنواع التدوين والترابط والأسبقية

الإعراب هو عملية تحليل سلسلة من الرموز ، معبراً عنها باللغات الطبيعية أو لغات الكمبيوتر والتي ستمنح قواعد نحوية رسمية . يعني تعبير التعبير في بنية البيانات تقييم التعبيرات الحسابية والمنطقية. أولاً ، دعنا نرى كيف تتم كتابة تعبير حسابي:

• 9 + 9
• سي بي

يمكن كتابة التعبير باستخدام ثوابت ومتغيرات ورموز يمكن أن تعمل كعامل تشغيل أو قوس. كل هذا التعبير يحتاج إلى اتباع مجموعة محددة من القواعد. وفقًا لهذه القاعدة ، يتم تحليل التعبير بناءً على القواعد.

يتم التعبير عن التعبير الحسابي في شكل تدوين . الآن ، هناك ثلاث طرق لكتابة تعبير في الحساب:

• تدوين Infix
• تدوين البادئة (البولندية)
• تدوين Postfix (عكس البولندية)

ومع ذلك ، عند كتابة التعبير ، يظل ناتج التعبير المطلوب كما هو. قبل البدء في أنواع التدوين ، دعنا نرى ما هي الترابطية والأسبقية في التعبير التحليل في بنية البيانات.

إذا كنت مبتدئًا ومهتمًا بمعرفة المزيد عن علم البيانات ، فراجع دورات علوم البيانات لدينا من أفضل الجامعات.

قراءة: الرسوم البيانية في بنية البيانات

الترابطية

قبل أن تبدأ ، عليك أن تعرف ما هي خاصية Associativity ؛ يزودك بقواعد إعادة ترتيب الأقواس في تعبير لتقديم إثبات صالح. هذا يعني أن إعادة ترتيب القوس يجب أن يعطي نفس قيمة المعادلة الأصلية. يوفر قاعدة صالحة لاستبدال عوامل التشغيل.

في تعبير يحتوي على عاملين أو أكثر ، لا تهم العملية المنفذة ما لم يتم تبادل تسلسل المعاملات. إذا كان التعبير مكتوبًا باستخدام الأقواس وفي اللاحم ، فإن تغيير الموضع لا يغير القيمة.

لأنه في اللغات الهندو أوروبية ، تُقرأ التعبيرات من اليسار إلى اليمين ، فإن معظم مشغلي infix هم ترابطون يسار ؛ يتم تقييم العوامل بنفس الأولوية. ارتفاع القوة هو القاعدة المستخدمة في اعتبار مشغلي infix. عوامل البادئة بشكل عام ترابطية لليمين ، وعوامل ما بعد الإصلاح هي ترابطية لليسار.

في بعض اللغات ، يتم إعطاء عوامل التشغيل والمعاملات قيمة متساوية ، حيث لا يعتبر الارتباط جعل تسلسل اللغة واضحًا. بينما في بعض اللغات ، تكون العوامل غير ترابطية ، وهذا يجعل استخدام التعبيرات المعقدة ضروريًا لاستخدام الأقواس ، مما يزيد من التعقيد للمبرمجين.

الأسبقية في هيكل البيانات

ترتيب الأسبقية يعني الترتيب الذي يجب على المشغلين اتباعه في بيان التعبيرات. يستخدم هذا بشكل شائع أثناء العمل مع Infix Notation.

في حالة المعامل < المشغل> <التشغيل> <المشغل> بين المشغلين ، يكون تفضيل تخصيص المشغل أمرًا صعبًا للغاية. ومن ثم ، يتم اتباع قواعد أسبقية عامل التشغيل للحساب. على سبيل المثال ، هنا ، الضرب له أسبقية أعلى ، وبعد ذلك يتم تنفيذ عملية الجمع.

• القاعدة الأكثر شيوعًا ولكنها ليست واضحة جدًا هي أنه يجب إجراء عملية الضرب والقسمة قبل الجمع والطرح. عادة ، يتم جمعها بنفس الطريقة ، لذلك يتم توفير أهمية متساوية لجميع المشغلين.
• بالنظر إلى هذه العملية بتنسيق منطقي ، يظهر الاختلاف في "و" و "أو." توفر العديد من اللغات أهمية متساوية ، حيث يتم إعطاء عملية "أو" أولوية أعلى. تعتبر بعض اللغات الضرب أو "&" أو "&" إضافة "أو" أسبقية متساوية ، حيث توفر معظم اللغات عمليات حسابية بأعلى أسبقية.
• يحدث التحميل الزائد بسبب عدم التخصيص الصحيح للأولوية. توفر العديد من اللغات أسبقية النفي (صواب / خطأ) أعلى من تعبيرات الجبر المتجه ، بينما توفر بعض اللغات أسبقية متساوية.

اقرأ أيضًا: أفكار مشروع هيكل البيانات

أنواع التدوين

الآن دعونا نتعلم كيف يقرر موضع المشغل نوع الترميز.

1. Infix تدوين

في Infix Notation ، يتم استخدام عوامل التشغيل بين المعاملات. أثناء قراءة تعبير ، يعد Infix Notation سهلًا جدًا للبشر. لكن الأمر يستغرق وقتًا ومساحة كبيرة لمعالجة حجة infix عندما يتعلق الأمر بخوارزمية الكمبيوتر. على سبيل المثال: p + q

< التشغيل> <المشغلات> <العمليات>

يحتاج تدوين Infix إلى معلومات إضافية لإجراء التقييم ؛ يتم إنشاء القواعد في لغة التعبير باستخدام عامل الارتباط على سبيل المثال: p * (q + r) / s

• تقترح قواعد الترابطية أن التعبير يجب أن يتم من اليسار إلى اليمين ، بحيث يتم الضرب في p قبل قسمة q.
• وبالمثل ، تقترح قواعد الأسبقية إجراء عملية الضرب والقسمة قبل إجراء عملية الجمع والطرح.

2. تدوين البادئة

هنا يتم كتابة العامل أولاً ، متبوعًا بالمعامل. ويسمى أيضًا بالتدوين البولندي. على سبيل المثال + pq

<المشغلات> <العمليات> <العمليات>

على سبيل المثال: p * (q + r) / s

يجب إجراء التقييم من اليسار إلى اليمين ، والأقواس لا تغير أو تغير نمط المعادلة. هنا ، يجب إكمال عملية الجمع قبل الضرب لأن الموضع "+" بقي من "*".

هنا ، ينفذ كل عامل عمليات على القيم الموجودة على يسارها مباشرة. على سبيل المثال ، يستخدم الرمز "+" أعلاه الحرفين "q" و "r". يمكننا تلخيص الأقواس لجعل هذا صريحًا:

((ص (qr +) *) ق /)

وبالتالي ، فإن "()" تأخذ في الاعتبار وتستخدم القيمتين بعد السابقة مباشرة لـ "p" ، ونتيجة +. وبالمثل ، فإن "/" تستخدم نتيجة تعبير الضرب و "s".

3. تدوين Postfix

تدوين Postfix ، في المقام الأول المعامل ، مكتوب ، متبوعًا بالمعامل. ويسمى أيضًا باسم التدوين البولندي العكسي ، على سبيل المثال ، pq +

<التشغيل> <العمليات> <المشغلات>

بالنسبة إلى Postfix ، نفس عملية البادئة للتعبير من اليسار إلى اليمين و "()" غير ضرورية. هنا ، يعمل المشغلون على أقرب قيمتين من اليمين. في المثال أدناه ، تمت إضافة الأقواس بشكل غير ضروري ، لتوضيح أنه لا يوجد تأثير على التقييم.

(/ (* p (+ qr)) s)

هنا "تقييم عامل التشغيل من اليسار إلى اليمين" تكون قيم العملية إلى اليمين ، وإذا كانت القيم نفسها تتضمن حسابات ، فحينئذٍ يكون هناك تغيير في ترتيب التقييم. أخذ المثال المذكور أعلاه ، راجع "/" هو العامل الأساسي على اليسار.

ينتظر حتى تكتمل عملية الضرب. وبشكل أساسي ، يجب إجراء عملية الضرب قبل بدء حساب القسمة (ومن المثال أعلاه ، من الواضح أن عملية الجمع يجب أن تكتمل قبل عملية الضرب).

لأن عوامل تدوين Postfix تستخدم القيمة الموجودة على يمينها ؛ أي قيم تتضمن عمليات حسابية ستكمل الحساب بالفعل بينما ننتقل إلى اليسار. لذلك ، يمكننا أن نستنتج أن حساب التعبير ليس مثل عملية عامل البادئة.

لتمييز جميع الرموز الثلاثة ، تأتي المعاملات بالترتيب نفسه ، ويجب نقل العوامل لتوفير المعنى الصحيح أثناء الحساب. يجب أخذ هذا في الاعتبار بشكل خاص عند النظر في العوامل غير المتماثلة "-" و "/" لتوضيح أن pq هي أي وقت مضى qr ما لم تكن لها نفس القيمة ؛ القيم معادلة لـ "pq -" أو "- pq"

P + q ≡ + pq pq +

على سبيل المثال:

Infix- p * q + r / s

بادئة - pq * rs / +

إصلاح آخر - + * pq / rs

أولاً ، لإجراء العملية ، اضرب p و q ثم اقسم r على s ، وأخيرًا ، أضف النتائج.

أدناه ملخصات الجدول بين الرموز الثلاثة ،

تدوين Infix	التدوين البولندي	عكس تدوين البولندية
ص + ف	+ ص	pq +
(ص + ف) * ص	+ * ص	pqr + *
ص * (ف + ص)	* ص + ريال قطري	pqr * + +
ص ÷ س + ص ÷ ث	+ ÷ pq ÷ rs	pq ÷ rs ÷ +
(pq) * (rs)	* -pq-rs	pq-rs- *

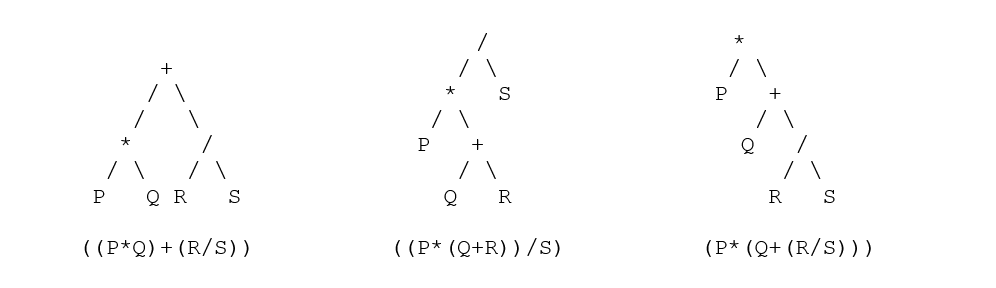
التحويل بين الترميزات

* لتوفير رؤية واضحة ، تم إضافة الأقواس في التعبير ،

أقحم	بوستفيكس	اختصار
((p * q) + (r / s))	((pq *) (rs /) +)	(+ (* pq) (/ rs))
((p * (q + r)) / s)	((ص (qr +) *) ق /)	(/ (* p (+ qr)) s)
(ص * (س + (ص / ث)))	(ف (ف (ص /) +) *)	(* p (+ q (/ rs)))

• يمكنك البدء في التحويل مباشرة في الأشكال الموضوعة بين قوسين بواسطة عوامل التشغيل الموجودة بين قوسين ، على سبيل المثال (m + n) أو (mn +) أو (+ mn). كرر الآن هذا في جميع العوامل عن طريق إزالة الأقواس غير المرغوب فيها.
• استخدم الآن هذه الحيلة الموضحة أعلاه لتحويل الأشجار وتحليلها - أشجار التحليل المكافئة لكل عقدة هي:

الخروج: هيكل البيانات والخوارزمية في بايثون

خاتمة

يختلف تحليل التعبيرات في بنية البيانات و Infix و Postfix و Prefix في التعبيرات الحسابية تمامًا ولكن لها نفس طرق كتابة التعبيرات. معرفة هذه أمر أساسي في كتابة البرامج.

في لغة برمجة الكمبيوتر ، يتم اعتبار التعبير وتحليله من السلسلة. تتغير قاعدة الترابطية والأسبقية في اللغات المختلفة.

لماذا تختار دورة علوم البيانات مع upGrad؟

علم البيانات هو أحد المجالات المزدهرة في علوم الكمبيوتر. تحتاج الشركات إلى مبرمجين لديهم معرفة جيدة بالأساسيات ، وهو أمر أساسي للبرمجة بغض النظر عن لغة الترميز.

تركز upGrad على تقديم فصول ثاقبة وغنية بالمعلومات ، تغطي كل الاحتياجات الأساسية لتصبح عالم بيانات. برنامج upGrad التنفيذي في علوم البيانات لمدة 12 شهرًا . ، التي يقدمها IIIT Bangalore ، هي أول دورة معتمدة من NASSCOM في الهند ، والتي تأتي مع إرشاد شخصي 1: 1 من خبراء صناعة علوم البيانات ، تغطي جميع لغات البرمجة والأدوات والمكتبات الأساسية. يوفر لك أفضل أساس لبدء عملك في علم البيانات عالي الأجر.

ما هي هياكل البيانات؟

تُستخدم هياكل البيانات لتنظيم البيانات في الذاكرة. توجد عدة طرق لترتيب البيانات في الذاكرة ، بما في ذلك المصفوفات والقوائم والمكدسات وقوائم الانتظار وغيرها الكثير. بنية البيانات ليست لغة برمجة مثل C أو C ++ أو Java. بدلاً من ذلك ، إنها مجموعة من التقنيات التي يتم استخدامها لترتيب البيانات في الذاكرة بأي لغة برمجة. بنية البيانات هي طريقة لتنظيم البيانات ومعالجتها وتخزينها بكفاءة. قد يتم عبور عناصر البيانات ببساطة بمساعدة بنية البيانات. إنه أمر حاسم في تحسين سرعة البرنامج لأن المهمة الرئيسية للبرنامج هي حفظ واسترجاع بيانات المستخدم بأسرع ما يمكن.

ما هي الاستخدامات الواقعية لتحليل البيانات؟

تُعرف عملية تحويل البيانات من تنسيق إلى آخر باسم تحليل البيانات. يتم استخدامها على نطاق واسع في المجمعين لتحليل رمز الكمبيوتر وإنشاء رمز الجهاز. تُعرف عملية تحويل البيانات من تنسيق إلى آخر باسم تحليل البيانات. نظرًا لصعوبة فهم لغة HTML الأولية التي نتلقاها ، غالبًا ما يتم توظيف المحلل اللغوي في تجريف البيانات عبر الإنترنت. نحن نطلب تحويل البيانات إلى تنسيق يمكن للبشر قراءته. قد يعني هذا إنشاء تقارير باستخدام سلاسل أو جداول HTML لتوفير المعلومات الأكثر صلة.

كيف تساعد الترابطية والأسبقية في هيكلة البيانات؟

يتم تحديد ترتيب تقييم التعبيرات من خلال خاصيتين للمشغلين: الأسبقية والترابطية. تساعد الأسبقية في تحديد كيفية تجميع المصطلحات في التعبير وكيفية تقييم التعبير. نظرًا لأن معظم التعبيرات تستخدم إطار عمل BODMAS ، فإن بعض العوامل لها الأسبقية على غيرها. عندما يكون لمعاملين نفس الأسبقية في التعبير ، يتم تطبيق قاعدة الارتباط. وفقًا لتفضيل المترجم ، قد تكون الترابطية إما من اليسار إلى اليمين أو من اليمين إلى اليسار.