什麼是樸素貝葉斯分類器? 【舉例說明】
已發表: 2020-12-28當您從事機器學習 (ML)、深度學習 (DL)、從一組數據中挖掘數據、在 Python 上編程或進行自然語言處理 (NLP) 時,有很多實例需要您區分離散的基於特定屬性的對象。 分類器是用於此目的的機器學習模型。 樸素貝葉斯分類器是這篇博文的關鍵,我們將進一步學習。
貝葉斯定理
英國數學家托馬斯·貝葉斯牧師,貝葉斯定理是用來確定條件概率的數學公式,條件概率是一個結果發生的可能性是基於先前的結果。
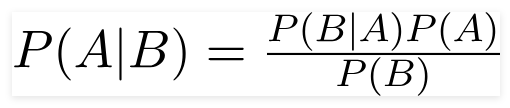
資源
使用這個公式,我們可以找到 B 發生時 A 的概率。
這裡,
A是命題;

B是證據;
P(A) 是命題的先驗概率;
P(B) 是證據的先驗概率;
P(A/B) 稱為後驗,並且
P(B/A) 稱為似然性。
因此,
P osterior = (Likelihood)(先驗概率中的命題)
_________________________________
證據先驗概率
這個公式假設預測變量或特徵是獨立的,一個人的存在不會影響另一個人的特徵。 因此,它被稱為“天真”。
顯示樸素貝葉斯分類器的示例
我們正在舉一個例子來更好地理解這個話題。
問題陳述:
我們正在創建一個分類器來描述文本是否與運動有關。
訓練數據有五句話:
| 句子 | 標籤 |
| “一場精彩的比賽” | 運動的 |
| “選舉結束了” | 不是運動 |
| “非常乾淨的比賽” | 運動的 |
| “這是一場勢均力敵的選舉” | 不是運動 |
| “一個乾淨但令人難忘的遊戲” | 運動的 |
在這裡,您需要找到句子“非常接近的遊戲”屬於哪個標籤?
樸素貝葉斯作為分類器計算句子“A very close game” is Sports 的概率為“ Not Sports”。
在數學上,我們想知道 P(體育 | 一場非常接近的比賽),即“非常接近的比賽”句子中標籤Sports的概率。
現在,下一步是計算概率。
但在此之前,讓我們先來看看一些概念。
特徵工程
我們需要首先確定在創建機器學習模型時要使用的功能。 特徵是提供給算法的文本中的信息塊。
在上面的示例中,我們將數據作為文本。 因此,我們需要將文本轉換為我們將執行計算的數字。
因此,我們將使用文本中出現的單詞的頻率來代替文本。 特徵將是這些單詞的數量。
應用貝葉斯定理
我們將使用單詞頻率的計數來轉換要計算的概率。 為此,我們將使用貝葉斯定理和一些基本的概率概念。
P(A/B) = P(B/A) x P(A)
______________
前鋒(乙)
我們有 P(體育 | 一場非常接近的比賽),並且通過使用貝葉斯定理,我們將抵消條件概率:
P(體育/非常接近的比賽)= P(非常接近的比賽/體育)x P(體育)
____________________________
P(非常接近的遊戲)
我們將放棄兩個標籤的除數相同並進行比較
P(非常接近的比賽/體育)x P(體育)
和
P(非常接近的比賽/非運動)x P(非運動)
我們可以通過計算句子“A very close game”出現在標籤“Sports”中的計數來計算概率。 要確定 P(非常接近的遊戲 | 體育),請將其除以總數。
但是,在訓練數據中,“非常接近的遊戲”似乎沒有出現在任何地方,所以這個概率為零。
如果我們要分類的每個句子都存在於訓練數據中,該模型將沒有多大用處。
樸素貝葉斯分類器
現在來到這裡的核心部分,“天真”。 句子中的每個單詞都是獨立的,我們不是在看整個句子,而是看單個單詞。 了解有關樸素貝葉斯分類器的更多信息。
P(非常接近的遊戲)= P(a)x P(非常)x P(接近)x P(遊戲)
這個假設也很強大和有用。 下一步是申請:
P(非常接近的比賽/體育) = P(a/體育) x P(非常/體育) x P(接近/體育) x P(比賽/體育)
這些單獨的單詞在我們可以計算的訓練數據中多次出現。
計算概率
最後一步是計算概率並查看哪個更大。
首先,我們計算標籤的先驗概率:對於給定訓練數據中的句子。 它是Sports P(Sports)的概率為 ⅗,P(Not Sports)的概率為 ⅖。
在計算 P(遊戲/體育)時,我們計算“遊戲”一詞在體育文本(此處為 2)中出現的次數除以體育中的詞(11)。

P(遊戲/運動)= 2/11
但是,任何體育文本中都沒有“接近”這個詞!
這意味著 P (close | Sports) = 0 並且不方便,因為我們會將它與其他概率相乘,
P(a/體育) x P(非常/體育) x 0 x P(遊戲/體育)
最終結果將為 0,整個計算將無效。 但這不是我們想要的,所以我們尋求其他方式。
拉普拉斯平滑
我們可以通過拉普拉斯平滑消除上述問題,我們將對每個計數加 1; 所以它永遠不會是零。
我們將可能的數字詞添加到除數,除數不會超過1。
在這種情況下,可能的單詞集是
['a', 'great', 'very', 'over', 'it', 'but', 'game', 'match', 'clean', '選舉', 'close', 'the', '是','忘記'] 。
可能的字數為 14; 通過應用拉普拉斯平滑,
P(遊戲/運動) = 2+1
___________
11 + 14
最終結果:
| 單詞 | P(字|體育) | P(字|不是體育) |
| 一種 | (2 + 1) ÷ (11 + 14) | (1 + 1) ÷ (9 + 14) |
| 非常 | (1 + 1) ÷ (11 + 14) | (0 + 1) ÷ (9 + 14) |
| 關閉 | (0 + 1) ÷ (11 + 14) | (1 + 1) ÷ (9 + 14) |
| 遊戲 | (2 + 1) ÷ (11 + 14) | (0 + 1) ÷ (9 + 14) |
現在,將所有概率相乘以找出哪個更大:
P(a/體育) x P(非常/體育) x P(遊戲/體育)x P(遊戲/體育)x P(體育)
= 2.76 x 10 ^-5
= 0.0000276
P(a/非運動)x P(非常/非運動)x P(遊戲/非運動)x P(遊戲/非運動)x P(非運動)
= 0.572 x 10 ^-5
= 0.00000572
因此,我們最終得到了我們的分類器,它給出了“非常接近的遊戲”標籤 Sports,因為它的概率很高,我們推斷該句子屬於 Sports 類別。
結帳:機器學習模型解釋
樸素貝葉斯分類器的類型
現在我們已經了解了樸素貝葉斯分類器是什麼並且也看過一個例子,讓我們看看它的類型:
1.多項樸素貝葉斯分類器
這主要用於文檔分類問題,文檔是否屬於政治、體育、技術等類別。該分類器使用的預測器是文檔中單詞的頻率。
2.伯努利樸素貝葉斯分類器
這類似於多項式樸素貝葉斯分類器,但其預測變量是布爾變量。 我們用來預測類變量的參數只取值是或否。 例如,一個詞是否出現在文本中。
3.高斯樸素貝葉斯分類器
當預測變量取一個常數值時,我們假設這些值是從高斯分佈中採樣的。
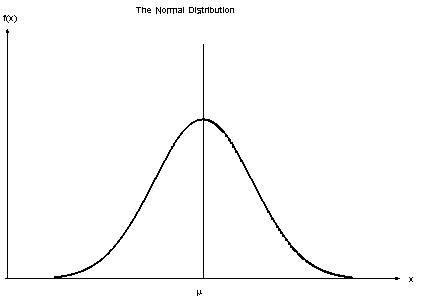
資源

由於數據集中存在的值發生變化,條件概率公式變為,
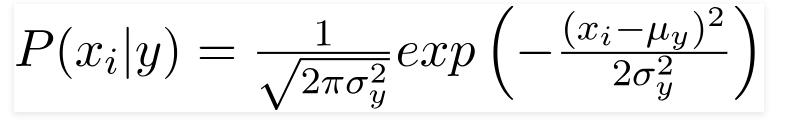
資源
結論
我們希望我們可以指導您了解什麼是樸素貝葉斯分類器以及如何使用它對文本進行分類。 這種簡單的方法在分類問題中創造了奇蹟。 無論您是否是機器學習專家,您都可以構建自己的樸素貝葉斯分類器,而無需花費數小時進行編碼。
如果您有興趣了解更多信息,請查看 Upgrad 在機器學習方面的獨家程序。 使用 upGrad 學習分類器:通過機器學習知識和深度學習技能提升您的職業生涯。 在upGrad 教育列兵。 有限公司,我們提供由行業專家精心設計和指導的認證計劃。
- 這個 240 多個小時的密集課程專為在職專業人士設計。
- 您將參與五個以上的行業項目和案例研究。
- 您將獲得 360 度的職業支持,並配有專門的學生成功導師和職業導師。
- 您將獲得安置方面的幫助,並學習建立一份強有力的簡歷。
現在申請!
