Apa itu Pengklasifikasi Naive Bayes? [Dijelaskan Dengan Contoh]
Diterbitkan: 2020-12-28Ada begitu banyak contoh ketika Anda mengerjakan pembelajaran mesin (ML), pembelajaran mendalam (DL), menambang data dari kumpulan data, pemrograman dengan Python, atau melakukan pemrosesan bahasa alami (NLP) di mana Anda diharuskan untuk membedakan diskrit objek berdasarkan atribut tertentu. Classifier adalah model pembelajaran mesin yang digunakan untuk tujuan tersebut. Pengklasifikasi Naive Bayes adalah inti dari posting blog ini yang akan kita pelajari lebih lanjut.
Teorema Bayes
Ahli matematika Inggris Pendeta Thomas Bayes, teorema Bayes adalah rumus matematika yang digunakan untuk menentukan probabilitas bersyarat, yang merupakan kemungkinan hasil yang terjadi berdasarkan hasil sebelumnya.
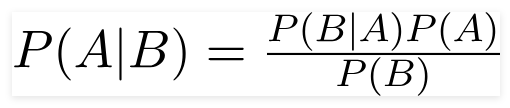
Sumber
Dengan menggunakan rumus ini, kita dapat menemukan probabilitas A ketika B telah terjadi.
Di Sini,
A adalah proposisi;

B adalah bukti;
P(A) adalah probabilitas proposisi sebelumnya;
P(B) adalah probabilitas bukti sebelumnya;
P(A/B) disebut posterior dan
P(B/A) disebut kemungkinan.
Karenanya,
P osterior = (Kemungkinan)(Proposisi dalam probabilitas sebelumnya)
_________________________________
Bukti Probabilitas sebelumnya
Rumus ini mengasumsikan bahwa prediktor atau fitur independen, dan kehadiran seseorang tidak memengaruhi fitur orang lain. Oleh karena itu, ini disebut 'naif.'
Contoh Menampilkan Pengklasifikasi Naive Bayes
Kami mengambil contoh pemahaman yang lebih baik tentang topik tersebut.
Pernyataan masalah:
Kami membuat pengklasifikasi yang menggambarkan apakah teks tentang olahraga atau tidak.
Data pelatihan memiliki lima kalimat:
| Kalimat | Label |
| “Permainan yang bagus” | Olahraga |
| “Pemilu sudah selesai” | Bukan olahraga |
| “Pertandingan yang sangat bersih” | Olahraga |
| “Itu adalah pemilihan yang ketat” | Bukan olahraga |
| “Permainan yang bersih tapi bisa dilupakan” | Olahraga |
Di sini, Anda perlu menemukan kalimat 'Permainan yang sangat dekat' dari label apa?
Naive Bayes, sebagai pengklasifikasi, menghitung probabilitas kalimat “Permainan yang sangat dekat” adalah Olahraga dengan probabilitas ' Bukan Olahraga.'
Secara matematis, kita ingin mengetahui P (Olahraga | permainan yang sangat dekat), probabilitas label Olahraga dalam kalimat “Permainan yang sangat dekat”.
Sekarang, langkah selanjutnya adalah menghitung probabilitas.
Tapi sebelum itu, mari kita lihat beberapa konsep.
Rekayasa Fitur
Kita harus terlebih dahulu menentukan fitur yang akan digunakan saat membuat model pembelajaran mesin. Fitur adalah potongan informasi dari teks yang diberikan ke algoritma.
Dalam contoh di atas, kami memiliki data sebagai teks. Jadi, kita perlu mengubah teks menjadi angka di mana kita akan melakukan perhitungan.
Oleh karena itu, alih-alih teks, kami akan menggunakan frekuensi kata-kata yang muncul dalam teks. Fiturnya adalah jumlah kata-kata ini.
Menerapkan Teorema Bayes
Kami akan mengonversi probabilitas yang akan dihitung menggunakan hitungan frekuensi kata. Untuk ini, kita akan menggunakan Teorema Bayes dan beberapa konsep dasar probabilitas.
P(A/B) = P(B/A) x P(A)
______________
P(B)
Kami memiliki P (Olahraga | permainan yang sangat dekat), dan dengan menggunakan teorema Bayes, kami akan melawan probabilitas bersyarat:
P (olahraga/permainan yang sangat dekat) = P(permainan yang sangat dekat/olahraga) x P(olahraga)
____________________________
P (permainan yang sangat dekat)
Kami akan mengabaikan pembagi yang sama untuk kedua label dan membandingkan
P(permainan yang sangat dekat/Olahraga) x P(Olahraga)
Dengan
P (permainan yang sangat dekat/ Bukan Olahraga) x P (Bukan Olahraga)
Kita dapat menghitung probabilitas dengan menghitung hitungan kalimat "Permainan yang sangat dekat" muncul di label 'Olahraga'. Untuk menentukan P (permainan yang sangat dekat | Olahraga), bagi dengan totalnya.
Tapi, dalam data pelatihan, 'Permainan yang sangat dekat' tidak muncul di mana pun sehingga probabilitas ini adalah nol.
Model tidak akan banyak berguna tanpa setiap kalimat yang ingin kita klasifikasikan ada dalam data pelatihan.
Pengklasifikasi Naive Bayes
Sekarang sampai pada bagian inti di sini, ' Naif.' Setiap kata dalam sebuah kalimat tidak bergantung pada yang lain, kita tidak melihat keseluruhan kalimat, tetapi pada satu kata. Pelajari lebih lanjut tentang pengklasifikasi bayes naif.
P(permainan sangat dekat) = P(a) x P(sangat) x P(dekat) x P(permainan)
Anggapan ini kuat dan berguna juga. Langkah selanjutnya adalah menerapkan:
P(permainan yang sangat dekat/Olahraga) = P(a/Olahraga) x P(sangat/Olahraga) x P(dekat/Olahraga) x P(permainan/Olahraga)
Kata-kata individual ini muncul berkali-kali dalam data pelatihan yang dapat kita hitung.
Komputasi Probabilitas
Langkah terakhir adalah menghitung probabilitas dan melihat mana yang lebih besar .
Pertama, kami menghitung probabilitas apriori dari label: untuk kalimat dalam data pelatihan yang diberikan. Peluang menjadi Olahraga P (Olahraga) adalah , dan P (Bukan Olahraga) adalah .
Saat menghitung P (permainan/Olahraga), kami menghitung berapa kali kata “permainan” muncul dalam teks Olahraga (di sini 2) dibagi dengan kata-kata dalam olahraga (11).

P(permainan/Olahraga) = 2/11
Tapi, kata "tutup" tidak ada dalam teks Olahraga apa pun!
Ini berarti P (close | Sports) = 0 dan tidak nyaman karena kita akan mengalikannya dengan probabilitas lain,
P(a/Olahraga) x P(sangat/Olahraga) x 0 x P(permainan/Olahraga)
Hasil akhirnya akan menjadi 0, dan seluruh perhitungan akan dibatalkan. Tapi ini bukan yang kami inginkan, jadi kami mencari jalan lain.
Penghalusan Laplace
Kami dapat menghilangkan masalah di atas dengan pemulusan Laplace, di mana kami akan menjumlahkan 1 untuk setiap hitungan; sehingga tidak pernah nol.
Kami akan menambahkan kemungkinan kata angka ke pembagi, dan pembagian tidak akan lebih dari 1.
Dalam hal ini, himpunan kata yang mungkin adalah
['a', 'hebat', 'sangat', 'lebih', 'itu', 'tetapi', 'permainan', 'cocok', 'bersih', 'pemilihan', 'tutup', 'yang', ' adalah', 'dilupakan'] .
Jumlah kata yang mungkin adalah 14; dengan menerapkan pemulusan Laplace,
P(permainan/Olahraga) = 2+1
___________
11 + 14
Hasil akhir:
| Kata | P (kata | Olahraga) | P (kata | Bukan Olahraga) |
| Sebuah | (2 + 1) (11 + 14) | (1 + 1) (9 + 14) |
| sangat | (1 + 1) (11 + 14) | (0 + 1) (9 + 14) |
| menutup | (0 + 1) (11 + 14) | (1 + 1) (9 + 14) |
| permainan | (2 + 1) (11 + 14) | (0 + 1) (9 + 14) |
Sekarang, mengalikan semua probabilitas untuk menemukan mana yang lebih besar:
P(a/Olahraga) x P(sangat/Olahraga) x P(permainan/Olahraga)x P(permainan/Olahraga)x P(Olahraga)
= 2,76 x 10 ^-5
= 0,0000276
P(a/Non Olahraga) x P(sangat/ Non Olahraga) x P(game/ Non Olahraga)x P(game/ Non Olahraga)x P(Non Olahraga)
= 0,572 x 10 ^-5
= 0,00000572
Oleh karena itu, kami akhirnya mendapatkan pengklasifikasi kami yang memberi "Permainan yang sangat dekat" label Olahraga karena probabilitasnya tinggi dan kami menyimpulkan bahwa kalimat tersebut termasuk dalam kategori Olahraga.
Lihat: Model Pembelajaran Mesin Dijelaskan
Jenis Pengklasifikasi Naive Bayes
Sekarang setelah kita memahami apa itu Naive Bayes Classifier dan telah melihat contohnya juga, mari kita lihat jenisnya:
1. Pengklasifikasi Naive Bayes Multinomial
Ini banyak digunakan untuk masalah klasifikasi dokumen, apakah suatu dokumen termasuk dalam kategori seperti politik, olahraga, teknologi, dll. Prediktor yang digunakan oleh pengklasifikasi ini adalah frekuensi kata dalam dokumen.
2. Pengklasifikasi Bernoulli Naive Bayes
Ini mirip dengan Multinomial Naive Bayes Classifier, tetapi prediktornya adalah variabel boolean. Parameter yang kita gunakan untuk memprediksi variabel kelas mengambil nilai ya atau tidak saja. Misalnya, apakah sebuah kata muncul dalam sebuah teks atau tidak.
3. Pengklasifikasi Gaussian Naive Bayes
Ketika prediktor mengambil nilai konstan, kami berasumsi bahwa nilai-nilai ini diambil dari distribusi Gaussian.
Sumber

Karena nilai yang ada dalam kumpulan data berubah, rumus probabilitas bersyarat berubah menjadi,
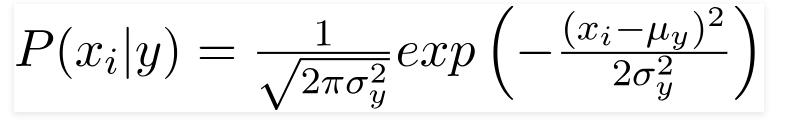
Sumber
Kesimpulan
Kami harap kami dapat memandu Anda tentang apa itu Naive Bayes Classifier dan bagaimana menggunakannya untuk mengklasifikasikan teks. Metode sederhana ini bekerja sangat baik dalam masalah klasifikasi. Baik Anda ahli Pembelajaran Mesin atau bukan, Anda dapat membuat Pengklasifikasi Naive Bayes Anda sendiri tanpa menghabiskan waktu berjam-jam untuk coding.
Jika Anda tertarik untuk mempelajari lebih lanjut, lihat program eksklusif Upgrade dalam pembelajaran mesin. Pengklasifikasi Pembelajaran dengan upGrad: Tingkatkan karier Anda dengan pengetahuan tentang pembelajaran mesin dan keterampilan pembelajaran Mendalam Anda. Di upGrad Education Pvt. Ltd. , kami menawarkan program sertifikasi yang dirancang dan dibimbing dengan cermat oleh pakar industri.
- Kursus intensif 240+ jam ini dirancang khusus untuk para profesional yang bekerja.
- Anda akan mengerjakan lebih dari lima proyek industri dan studi kasus.
- Anda akan menerima dukungan karir 360 derajat dengan mentor kesuksesan siswa dan mentor karir yang berdedikasi.
- Anda akan mendapatkan bantuan untuk penempatan Anda dan belajar membuat resume yang kuat.
Daftar Sekarang!
