Qu'est-ce que le classificateur Naive Bayes ? [Expliqué avec exemple]
Publié: 2020-12-28Il y a tellement de cas où vous travaillez sur l'apprentissage automatique (ML), l'apprentissage en profondeur (DL), l'extraction de données à partir d'un ensemble de données, la programmation sur Python ou le traitement du langage naturel (NLP) dans lequel vous devez différencier des objets basés sur des attributs spécifiques. Un classificateur est un modèle d'apprentissage automatique utilisé à cette fin. Le classificateur Naive Bayes est au cœur de cet article de blog que nous apprendrons plus loin.
Théorème de Bayes
Le mathématicien britannique révérend Thomas Bayes, le théorème de Bayes est une formule mathématique utilisée pour déterminer la probabilité conditionnelle, qui est la probabilité qu'un résultat se produise sur la base d'un résultat précédent.
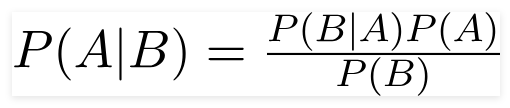
La source
En utilisant cette formule, nous pouvons trouver la probabilité de A lorsque B s'est produit.
Ici,
A est la proposition;

B est la preuve ;
P(A) est la probabilité a priori de proposition ;
P(B) est la probabilité a priori de la preuve ;
P(A/B) est appelé postérieur et
P(B/A) est appelé la vraisemblance.
D'où,
Postérieur = (Vraisemblance)(Proposition en probabilité a priori)
_________________________________
Preuve Probabilité a priori
Cette formule suppose que les prédicteurs ou les caractéristiques sont indépendants et que la présence de l'un n'affecte pas la caractéristique d'un autre. Par conséquent, il est appelé « naïf ».
Exemple d'affichage du classificateur Bayes naïf
Nous prenons l'exemple d'une meilleure compréhension du sujet.
Énoncé du problème :
Nous créons un classificateur qui indique si un texte concerne le sport ou non.
Les données d'entraînement comportent cinq phrases :
| Phrase | Étiqueter |
| "Un super jeu" | Des sports |
| "L'élection était finie" | Pas de sport |
| "Match très propre" | Des sports |
| "C'était une élection serrée" | Pas de sport |
| "Un jeu propre mais oubliable" | Des sports |
Ici, vous devez trouver la phrase 'Un jeu très proche' est de quelle étiquette ?
Naive Bayes, en tant que classificateur, calcule la probabilité de la phrase "Un jeu très serré" est Sportif avec la probabilité " Pas Sportif".
Mathématiquement, on veut connaître P (Sports | un jeu très serré), probabilité du label Sports dans la phrase « Un jeu très serré ».
Maintenant, la prochaine étape consiste à calculer les probabilités.
Mais avant cela, examinons quelques concepts.
Ingénierie des fonctionnalités
Nous devons d'abord déterminer les fonctionnalités à utiliser lors de la création d'un modèle d'apprentissage automatique. Les caractéristiques sont les morceaux d'informations du texte donné à l'algorithme.
Dans l'exemple ci-dessus, nous avons des données sous forme de texte. Nous devons donc convertir le texte en nombres dans lesquels nous effectuerons des calculs.
Par conséquent, au lieu du texte, nous utiliserons les fréquences des mots apparaissant dans le texte. Les traits seront le nombre de ces mots.
Application du théorème de Bayes
Nous allons convertir la probabilité à calculer en utilisant le décompte de la fréquence des mots. Pour cela, nous utiliserons le théorème de Bayes et quelques concepts de base de probabilité.
P(A/B) = P(B/A) x P(A)
______________
P(B)
Nous avons P (Sports | un jeu très proche), et en utilisant le théorème de Bayes, nous allons annuler la probabilité conditionnelle :
P (sport/un jeu très serré) = P(un jeu très serré/un sport) x P(sport)
____________________________
P (un jeu très serré)
Nous allons abandonner le même diviseur pour les deux étiquettes et comparer
P(un jeu très serré/Sports) x P(Sports)
Avec
P(un jeu très serré/Pas de sport) x P(Pas de sport)
On peut calculer les probabilités en calculant les décomptes de la phrase « Un jeu très serré » émerge dans l'étiquette « Sports ». Pour déterminer P (un jeu très proche | Sports), divisez-le par le total.
Mais, dans les données d'entraînement, "Un jeu très serré" n'apparaît nulle part, donc cette probabilité est nulle.
Le modèle ne sera pas très utile sans que chaque phrase que nous voulons classer soit présente dans les données d'apprentissage.
Classificateur naïf de Bayes
Vient maintenant la partie centrale ici, " Naïf ". Chaque mot d'une phrase est indépendant de l'autre, nous ne regardons pas les phrases entières, mais des mots simples. En savoir plus sur le classificateur naïf bayes.
P(un jeu très proche) = P(a) x P(très) x P(proche) x P(jeu)
Cette présomption est puissante et utile aussi. L'étape suivante consiste à appliquer :
P(un jeu très proche/Sports) = P(a/Sports) x P(très/Sports) x P(proche/Sports) x P(jeu/Sports)
Ces mots individuels apparaissent plusieurs fois dans les données d'apprentissage que nous pouvons calculer.
Probabilité de calcul
L'étape finale consiste à calculer les probabilités et à déterminer laquelle est la plus grande .
Tout d'abord, nous calculons la probabilité a priori des étiquettes : pour les phrases dans les données d'apprentissage données. La probabilité qu'il s'agisse de Sports P (Sports) sera de ⅗, et P (Non Sports) sera de ⅖.
Lors du calcul de P (jeu/Sports), on compte les fois où le mot « jeu » apparaît dans le texte Sports (ici 2) divisé par les mots dans sports (11).

P(jeu/sport) = 2/11
Mais, le mot "fermer" n'est présent dans aucun texte sportif !
Cela signifie que P (proche | Sports) = 0 et n'est pas pratique car nous allons le multiplier par d'autres probabilités,
P(a/Sports) x P(très/Sports) x 0 x P(jeu/Sports)
Le résultat final sera 0 et l'ensemble du calcul sera annulé. Mais ce n'est pas ce que nous voulons, alors nous cherchons un autre moyen de contourner.
Lissage de Laplace
Nous pouvons éliminer le problème ci-dessus avec le lissage de Laplace, où nous additionnerons 1 à chaque compte ; pour qu'il ne soit jamais nul.
Nous ajouterons les mots numériques possibles au diviseur, et la division ne sera pas supérieure à 1.
Dans ce cas, l'ensemble des mots possibles est
['a', 'super', 'très', 'over', 'it', 'but', 'game', 'match', 'clean', 'election', 'close', 'the', ' était', 'oubliable'] .
Le nombre de mots possible est de 14 ; en appliquant un lissage de Laplace,
P(jeu/sport) = 2+1
___________
11 + 14
Résultat final:
| Mot | P (mot | Sports) | P (mot | Pas de sport) |
| une | (2 + 1) ÷ (11 + 14) | (1 + 1) ÷ (9 + 14) |
| très | (1 + 1) ÷ (11 + 14) | (0 + 1) ÷ (9 + 14) |
| Fermer | (0 + 1) ÷ (11 + 14) | (1 + 1) ÷ (9 + 14) |
| Jeu | (2 + 1) ÷ (11 + 14) | (0 + 1) ÷ (9 + 14) |
Maintenant, en multipliant toutes les probabilités pour trouver laquelle est la plus grande :
P(a/Sports) x P(très/Sports) x P(jeu/Sports)x P(jeu/Sports)x P(Sports)
= 2,76 × 10 ^-5
= 0,0000276
P(a/Non sportif) x P(très/non sportif) x P(jeu/non sportif)x P(jeu/non sportif)x P(non sportif)
= 0,572 x 10 ^-5
= 0,00000572
Par conséquent, nous avons enfin notre classificateur qui donne à "Un jeu très proche" l'étiquette Sports car sa probabilité est élevée et nous en déduisons que la phrase appartient à la catégorie Sports.
Paiement : Explication des modèles d'apprentissage automatique
Types de classificateur Bayes naïf
Maintenant que nous avons compris ce qu'est un classificateur Naive Bayes et que nous avons également vu un exemple, voyons les types de celui-ci :
1. Classificateur Bayes naïf multinomial
Ceci est principalement utilisé pour les problèmes de classification de documents, qu'un document appartienne à des catégories telles que la politique, le sport, la technologie, etc. Le prédicteur utilisé par ce classificateur est la fréquence des mots dans le document.
2. Classificateur naïf de Bernoulli Bayes
Ceci est similaire au classificateur multinomial Naive Bayes, mais ses prédicteurs sont des variables booléennes. Les paramètres que nous utilisons pour prédire la variable de classe prennent les valeurs oui ou non uniquement. Par exemple, si un mot apparaît dans un texte ou non.
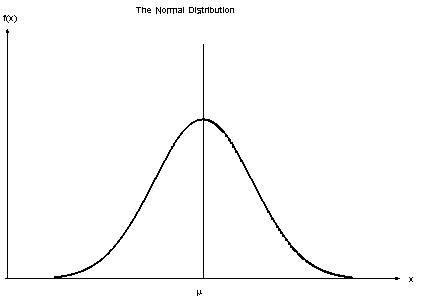
3. Classificateur gaussien naïf de Bayes
Lorsque les prédicteurs prennent une valeur constante, nous supposons que ces valeurs sont échantillonnées à partir d'une distribution gaussienne.
La source

Étant donné que les valeurs présentes dans l'ensemble de données changent, la formule de probabilité conditionnelle devient :
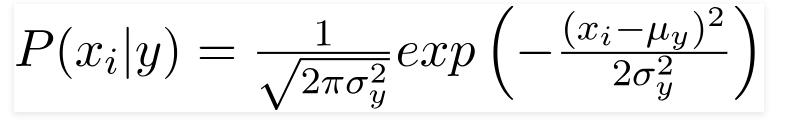
La source
Conclusion
Nous espérons que nous pourrons vous guider sur ce qu'est le classificateur Naive Bayes et comment il est utilisé pour classer le texte. Cette méthode simple fait des merveilles dans les problèmes de classification. Que vous soyez un expert en apprentissage automatique ou non, vous pouvez créer votre propre classificateur Naive Bayes sans passer des heures à coder.
Si vous souhaitez en savoir plus, consultez les programmes exclusifs d'Upgrad en apprentissage automatique. Classificateurs d'apprentissage avec upGrad : donnez un coup de pouce à votre carrière grâce à la connaissance de l'apprentissage automatique et à vos compétences en apprentissage profond. Chez upGrad Education Pvt. Ltd. , nous offrons un programme de certification soigneusement conçu et encadré par des experts de l'industrie.
- Ce cours intensif de plus de 240 heures est spécialement conçu pour les professionnels en activité.
- Vous travaillerez sur plus de cinq projets industriels et études de cas.
- Vous recevrez un soutien de carrière à 360 degrés avec un mentor dédié à la réussite des étudiants et un mentor de carrière.
- Vous obtiendrez de l'aide pour votre placement et apprendrez à construire un CV solide.
Appliquer maintenant!
