Was ist der Naive-Bayes-Klassifikator? [Erklärt mit Beispiel]
Veröffentlicht: 2020-12-28Es gibt so viele Fälle, in denen Sie an maschinellem Lernen (ML), Deep Learning (DL), dem Mining von Daten aus einer Reihe von Daten, der Programmierung mit Python oder der Verarbeitung natürlicher Sprache (NLP) arbeiten, in denen Sie diskret unterscheiden müssen Objekte basierend auf bestimmten Attributen. Ein Klassifikator ist ein maschinelles Lernmodell, das für diesen Zweck verwendet wird. Der Naive-Bayes-Klassifikator ist der Kern dieses Blogbeitrags, den wir weiter lernen werden.
Satz von Bayes
Der britische Mathematiker Reverend Thomas Bayes, Bayes ' Theorem, ist eine mathematische Formel, die verwendet wird, um die bedingte Wahrscheinlichkeit zu bestimmen, die die Wahrscheinlichkeit ist, dass ein Ergebnis auf der Grundlage eines früheren Ergebnisses eintritt.
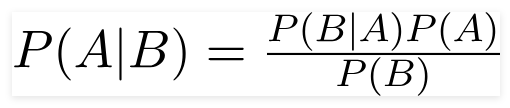
Quelle
Mit dieser Formel können wir die Wahrscheinlichkeit von A finden, wenn B eingetreten ist.
Hier,
A ist der Satz;

B ist der Beweis;
P(A) ist die vorherige Wahrscheinlichkeit des Satzes;
P(B) ist die vorherige Beweiswahrscheinlichkeit;
P(A/B) wird das hintere und genannt
P(B/A) wird Wahrscheinlichkeit genannt.
Somit,
P osterior = (Likelihood)(Proposition in A-priori-Wahrscheinlichkeit)
_________________________________
Evidence Prior-Wahrscheinlichkeit
Diese Formel geht davon aus, dass die Prädiktoren oder Merkmale unabhängig sind und die Anwesenheit des einen das Merkmal eines anderen nicht beeinflusst. Daher wird es "naiv" genannt.
Beispiel für die Anzeige des Naive-Bayes-Klassifikators
Wir nehmen ein Beispiel für ein besseres Verständnis des Themas.
Problemstellung:
Wir erstellen einen Klassifikator, der anzeigt, ob es in einem Text um Sport geht oder nicht.
Die Trainingsdaten bestehen aus fünf Sätzen:
| Satz | Etikette |
| „Ein tolles Spiel“ | Sport |
| „Die Wahl war vorbei“ | Nicht Sport |
| „Sehr sauberes Spiel“ | Sport |
| „Es war eine knappe Wahl“ | Nicht Sport |
| „Ein sauberes, aber unvergessliches Spiel“ | Sport |
Hier müssen Sie den Satz „Ein sehr enges Spiel“ von welchem Label finden?
Naive Bayes berechnet als Klassifikator die Wahrscheinlichkeit des Satzes „Ein sehr enges Spiel“ ist Sport mit der Wahrscheinlichkeit „ Nicht Sport“.
Mathematisch wollen wir P (Sport | ein sehr enges Spiel) wissen, die Wahrscheinlichkeit der Bezeichnung Sport im Satz „Ein sehr enges Spiel“.
Der nächste Schritt ist nun die Berechnung der Wahrscheinlichkeiten.
Aber vorher werfen wir einen Blick auf einige Konzepte.
Feature-Engineering
Wir müssen zuerst die Funktionen bestimmen, die bei der Erstellung eines Modells für maschinelles Lernen verwendet werden sollen. Features sind die Informationsbrocken aus dem Text, die dem Algorithmus übergeben werden.
Im obigen Beispiel haben wir Daten als Text. Also müssen wir den Text in Zahlen umwandeln, in denen wir Berechnungen durchführen.
Daher verwenden wir anstelle von Text die Häufigkeiten der im Text vorkommenden Wörter. Die Merkmale werden die Anzahl dieser Wörter sein.
Anwendung des Satzes von Bayes
Wir werden die zu berechnende Wahrscheinlichkeit anhand der Anzahl der Worthäufigkeiten umrechnen. Dazu verwenden wir das Theorem von Bayes und einige grundlegende Konzepte der Wahrscheinlichkeit.
P(A/B) = P(B/A) x P(A)
______________
P(B)
Wir haben P (Sport | ein sehr enges Spiel) und unter Verwendung des Satzes von Bayes werden wir die bedingte Wahrscheinlichkeit widerlegen:
P (Sport/ein sehr enges Spiel) = P(ein sehr enges Spiel/Sport) x P(Sport)
____________________________
P (ein sehr enges Spiel)
Wir lassen den Divisor gleich für beide Labels und vergleichen
P(ein sehr enges Spiel/Sport) x P(Sport)
Mit
P (ein sehr enges Spiel / kein Sport) x P (kein Sport)
Wir können die Wahrscheinlichkeiten berechnen, indem wir die Anzahl berechnen, die der Satz „Ein sehr enges Spiel“ in der Bezeichnung „Sport“ ergibt. Um P (ein sehr enges Spiel | Sport) zu bestimmen, teilen Sie es durch die Gesamtzahl.
Aber in den Trainingsdaten erscheint nirgendwo „Ein sehr enges Spiel“, also ist diese Wahrscheinlichkeit null.
Das Modell wird nicht viel nützen, wenn nicht jeder Satz, den wir klassifizieren wollen, in den Trainingsdaten vorhanden ist.
Naive Bayes-Klassifikator
Jetzt kommt hier der Kernteil, ' Naive'. Jedes Wort in einem Satz ist unabhängig vom anderen, wir betrachten nicht den ganzen Satz, sondern einzelne Wörter. Erfahren Sie mehr über den Naive-Bayes-Klassifikator.
P(ein sehr enges Spiel) = P(a) x P(sehr) x P(nah) x P(Spiel)
Diese Vermutung ist ebenso mächtig wie nützlich. Der nächste Schritt ist die Anwendung:
P(ein sehr enges Spiel/Sport) = P(a/Sport) x P(sehr/Sport) x P(nah/Sport) x P(Spiel/Sport)
Diese einzelnen Wörter erscheinen viele Male in den Trainingsdaten, die wir berechnen können.
Wahrscheinlichkeit berechnen
Der abschließende Schritt besteht darin, die Wahrscheinlichkeiten zu berechnen und zu prüfen, welche größer ist .
Zuerst berechnen wir die A-priori -Wahrscheinlichkeit der Labels: für die Sätze in den gegebenen Trainingsdaten. Die Wahrscheinlichkeit, dass es Sport P (Sport) ist, ist ⅗ und P (Nicht Sport) ist ⅖.
Bei der Berechnung von P (Spiel/Sport) zählen wir, wie oft das Wort „Spiel“ im Sporttext (hier 2) vorkommt, dividiert durch die Wörter in Sport (11).

P(Spiel/Sport) = 2/11
Aber das Wort „nahe“ kommt in keinem Sporttext vor !
Das bedeutet P (Schließen | Sport) = 0 und ist umständlich, da wir es mit anderen Wahrscheinlichkeiten multiplizieren werden,
P(a/Sport) x P(sehr/Sport) x 0 x P(Spiel/Sport)
Das Endergebnis ist 0 und die gesamte Berechnung wird annulliert. Aber das wollen wir nicht, also suchen wir einen anderen Weg.
Laplace-Glättung
Wir können das obige Problem mit der Laplace-Glättung beseitigen, bei der wir 1 zu jeder Zählung addieren; damit es nie null ist.
Wir werden die möglichen Zahlenwörter zum Divisor hinzufügen, und die Division wird nicht größer als 1 sein.
In diesem Fall sind die Menge möglicher Wörter
['a', 'great', 'very', 'over', 'it', 'but', 'game', 'match', 'clean', 'election', 'close', 'the', ' war', 'vergesslich'] .
Die mögliche Wortzahl beträgt 14; durch Anwendung von Laplace-Glättung,
P(Spiel/Sport) = 2+1
___________
11 + 14
Endergebnis:
| Wort | P (Wort | Sport) | P (Wort | Nicht Sport) |
| ein | (2 + 1) ÷ (11 + 14) | (1 + 1) ÷ (9 + 14) |
| sehr | (1 + 1) ÷ (11 + 14) | (0 + 1) ÷ (9 + 14) |
| nah dran | (0 + 1) ÷ (11 + 14) | (1 + 1) ÷ (9 + 14) |
| Spiel | (2 + 1) ÷ (11 + 14) | (0 + 1) ÷ (9 + 14) |
Multiplizieren Sie nun alle Wahrscheinlichkeiten, um herauszufinden, welche größer ist:
P(a/Sport) x P(sehr/Sport) x P(Spiel/Sport)x P(Spiel/Sport)x P(Sport)
= 2,76 x 10^-5
= 0,0000276
P(a/kein Sport) x P(sehr/kein Sport) x P(Spiel/kein Sport)x P(Spiel/kein Sport)x P(kein Sport)
= 0,572 x 10^-5
= 0,00000572
Daher haben wir endlich unseren Klassifikator, der „Ein sehr enges Spiel“ das Label Sport gibt, da seine Wahrscheinlichkeit hoch ist, und wir schließen daraus, dass der Satz zur Kategorie Sport gehört.
Checkout: Modelle für maschinelles Lernen erklärt
Arten von Naive-Bayes-Klassifikatoren
Nachdem wir nun verstanden haben, was ein Naive-Bayes-Klassifikator ist, und auch ein Beispiel gesehen haben, sehen wir uns die Typen davon an:
1. Multinomialer Naive-Bayes-Klassifikator
Dies wird hauptsächlich für Probleme mit der Dokumentklassifizierung verwendet, ob ein Dokument zu Kategorien wie Politik, Sport, Technologie usw. gehört. Der von diesem Klassifikator verwendete Prädiktor ist die Häufigkeit der Wörter im Dokument.
2. Bernoulli-Naive-Bayes-Klassifikator
Dies ähnelt dem multinomialen Naive-Bayes-Klassifikator, aber seine Prädiktoren sind boolesche Variablen. Die Parameter, die wir verwenden, um die Klassenvariable vorherzusagen, nehmen nur die Werte ja oder nein an. Zum Beispiel, ob ein Wort in einem Text vorkommt oder nicht.
3. Gaußscher Naive-Bayes-Klassifikator
Wenn die Prädiktoren einen konstanten Wert annehmen, nehmen wir an, dass diese Werte aus einer Gaußschen Verteilung stammen.
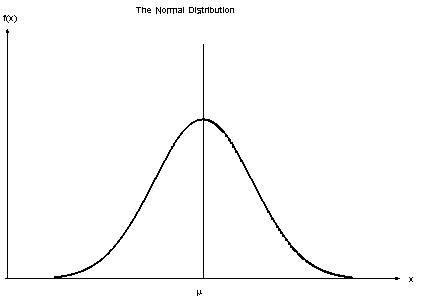
Quelle

Da sich die im Datensatz vorhandenen Werte ändern, ändert sich die bedingte Wahrscheinlichkeitsformel zu
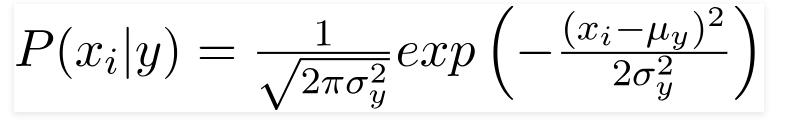
Quelle
Fazit
Wir hoffen, dass wir Ihnen zeigen konnten, was Naive Bayes Classifier ist und wie er zum Klassifizieren von Text verwendet wird. Diese einfache Methode wirkt Wunder bei Klassifizierungsproblemen. Egal, ob Sie ein Experte für maschinelles Lernen sind oder nicht, Sie können Ihren eigenen Naive-Bayes-Klassifikator erstellen, ohne Stunden mit dem Programmieren verbringen zu müssen.
Wenn Sie mehr erfahren möchten, sehen Sie sich die exklusiven Programme von Upgrad für maschinelles Lernen an. Lernende Klassifikatoren mit upGrad: Geben Sie Ihrer Karriere einen Schub mit dem Wissen über maschinelles Lernen und Ihren Deep-Learning-Fähigkeiten. Bei upGrad Education Pvt. Ltd. bieten wir ein Zertifizierungsprogramm an, das sorgfältig von Branchenexperten entwickelt und betreut wird.
- Dieser Intensivkurs mit mehr als 240 Stunden ist speziell für Berufstätige konzipiert.
- Sie arbeiten an mehr als fünf Industrieprojekten und Fallstudien.
- Sie erhalten eine 360-Grad-Karriereunterstützung mit einem engagierten Mentor für den Studienerfolg und einem Karrierementor.
- Sie erhalten Unterstützung für Ihr Praktikum und lernen, einen starken Lebenslauf aufzubauen.
Jetzt bewerben!
