Co to jest klasyfikator naiwny Bayesa? [Wyjaśniono z przykładem]
Opublikowany: 2020-12-28Jest tak wiele przypadków, gdy pracujesz nad uczeniem maszynowym (ML), uczeniem głębokim (DL), wydobywaniem danych z zestawu danych, programowaniem w Pythonie lub przetwarzaniem języka naturalnego (NLP), w których wymagane jest rozróżnienie dyskretnych obiekty na podstawie określonych atrybutów. Klasyfikator to model uczenia maszynowego używany w tym celu. Naiwny klasyfikator Bayesa jest sednem tego wpisu na blogu, o którym dowiemy się dalej.
Twierdzenie Bayesa
Brytyjski matematyk wielebny Thomas Bayes, twierdzenie Bayesa to matematyczny wzór używany do określenia prawdopodobieństwa warunkowego, które jest prawdopodobieństwem wystąpienia wyniku na podstawie poprzedniego wyniku.
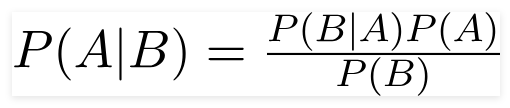
Źródło
Korzystając z tego wzoru, możemy znaleźć prawdopodobieństwo wystąpienia A, gdy wystąpi B.
Tutaj,
A to propozycja;

B jest dowodem;
P(A) jest prawdopodobieństwem a priori zdania;
P(B) to prawdopodobieństwo a priori dowodu;
P(A/B) nazywa się tylnym i
P(B/A) nazywamy prawdopodobieństwem.
Stąd,
P osterior = (Prawdopodobieństwo) (Propozycja z prawdopodobieństwem a priori)
_________________________________
Dowód Prawdopodobieństwo a priori
Ta formuła zakłada, że predyktory lub cechy są niezależne, a czyjaś obecność nie wpływa na inną cechę. Dlatego nazywa się to „naiwnym”.
Przykład wyświetlania naiwnego klasyfikatora Bayesa
Podajemy przykład lepszego zrozumienia tematu.
Oświadczenie o problemie:
Tworzymy klasyfikator, który pokazuje, czy tekst dotyczy sportu, czy nie.
Dane treningowe składają się z pięciu zdań:
| Wyrok | Etykieta |
| “Świetna gra” | Sporty |
| „Wybory się skończyły” | Nie sport |
| “Bardzo czysty mecz” | Sporty |
| „To były bliskie wybory” | Nie sport |
| “Czysta, ale niezapomniana gra” | Sporty |
Tutaj musisz znaleźć zdanie „Bardzo bliska gra” jakiej etykiety?
Naive Bayes, jako klasyfikator, oblicza prawdopodobieństwo zdania „bardzo wyrównana gra” to sport z prawdopodobieństwem „ nie jest sportem”.
Matematycznie chcemy poznać P (Sport | bardzo wyrównana gra), prawdopodobieństwo etykiety Sport w zdaniu „bardzo wyrównana gra”.
Teraz kolejnym krokiem jest obliczenie prawdopodobieństw.
Ale wcześniej przyjrzyjmy się kilku koncepcjom.
Inżynieria funkcji
Najpierw musimy określić funkcje, które będą używane podczas tworzenia modelu uczenia maszynowego. Cechy to fragmenty informacji z tekstu podanego do algorytmu.
W powyższym przykładzie mamy dane jako tekst. Musimy więc przekonwertować tekst na liczby, w których będziemy wykonywać obliczenia.
Dlatego zamiast tekstu użyjemy częstotliwości słów występujących w tekście. Cechą będzie liczba tych słów.
Stosowanie twierdzenia Bayesa
Obliczone prawdopodobieństwo przeliczymy na podstawie liczby słów. W tym celu użyjemy twierdzenia Bayesa i kilku podstawowych pojęć prawdopodobieństwa.
P(A/B) = P(B/A) x P(A)
______________
P(B)
Mamy P (Sport | bardzo wyrównana gra) i używając twierdzenia Bayesa skontrujemy prawdopodobieństwo warunkowe:
P (sport/bardzo wyrównana gra) = P(bardzo wyrównana gra/sport) x P(sport)
____________________________
P (bardzo wyrównana gra)
Porzucimy dzielnik taki sam dla obu etykiet i porównania
P (bardzo wyrównana gra/Sport) x P(Sport)
Z
P (bardzo wyrównana gra/Niesportowa) x P(Niesportowa)
Prawdopodobieństwa można obliczyć, obliczając zliczenia, w etykiecie „Sport” pojawia się zdanie „Bardzo wyrównana gra” . Aby określić P (bardzo wyrównana gra | Sport), podziel ją przez sumę.
Ale w danych treningowych „bardzo wyrównana gra” nie wydaje się nigdzie, więc to prawdopodobieństwo wynosi zero.
Model nie będzie zbyt przydatny, jeśli każde zdanie, które chcemy sklasyfikować, będzie obecne w danych uczących.
Naiwny klasyfikator Bayesa
Teraz pojawia się główna część, „ Naiwny”. Każde słowo w zdaniu jest niezależne od drugiego, nie patrzymy na całe zdania, ale na pojedyncze słowa. Dowiedz się więcej o naiwnym klasyfikatorze bayes.
P(bardzo wyrównana gra) = P(a) x P(bardzo) x P(zamknięta) x P(gra)
To założenie jest również potężne i użyteczne. Kolejnym krokiem jest zastosowanie:
P(bardzo bliska gra/Sport) = P(a/Sport) x P(bardzo/Sport) x P(Bardzo bliska/Sport) x P(Gra/Sport)
Te pojedyncze słowa pojawiają się wielokrotnie w danych treningowych, które możemy obliczyć.
Obliczanie prawdopodobieństwa
Ostatnim krokiem jest obliczenie prawdopodobieństw i sprawdzenie, które z nich jest większe .
Najpierw obliczamy prawdopodobieństwo a priori etykiet: dla zdań w danych treningowych. Prawdopodobieństwo, że będzie to sport P (sport) wyniesie ⅗, a P (nie sport) wyniesie ⅖.
Przy obliczaniu P (gra/sport) liczymy wystąpienie słowa „gra” w tekście Sport (tutaj 2) przez słowa w sporcie (11).

P (gra/sport) = 2/11
Ale słowo „zamknij” nie występuje w żadnym tekście o sporcie !
Oznacza to, że P (zamknij | Sport) = 0 i jest niewygodne, ponieważ pomnożymy to przez inne prawdopodobieństwa,
P(a/sport) x P(bardzo/sport) x 0 x P(gra/sport)
Wynik końcowy wyniesie 0, a całe obliczenie zostanie anulowane. Ale nie tego chcemy, więc szukamy innej drogi.
Wygładzanie Laplace'a
Powyższy problem możemy wyeliminować za pomocą wygładzania Laplace'a, gdzie do każdego zliczenia będziemy doliczać 1; aby nigdy nie było zera.
Do dzielnika dodamy możliwe słowa liczbowe, a dzielenie nie będzie większe niż 1.
W tym przypadku zestaw możliwych słów to
['a', 'super', 'very', 'over', 'it', 'but', 'game', 'match', 'clean', 'election', 'close', 'the', ' było”, „niezapomniane”] .
Możliwa liczba słów to 14; poprzez zastosowanie wygładzenia Laplace'a,
P (gra/sport) = 2+1
___________
11 + 14
Ostateczny wynik:
| Słowo | P (słowo | Sport) | P (słowo | Nie sport) |
| a | (2 + 1) ÷ (11 + 14) | (1 + 1) ÷ (9 + 14) |
| bardzo | (1 + 1) ÷ (11 + 14) | (0+1) ÷ (9+14) |
| blisko | (0+1) ÷ (11+14) | (1 + 1) ÷ (9 + 14) |
| gra | (2 + 1) ÷ (11 + 14) | (0+1) ÷ (9+14) |
Teraz mnożąc wszystkie prawdopodobieństwa, aby znaleźć większe:
P(a/sport) x P(bardzo/sport) x P(gra/sport)x P(gra/sport)x P(sport)
= 2,76 x 10 ^-5
= 0,0000276
P(a/niesportowe) x P(bardzo/niesportowe) x P(gra/niesportowe)x P(gra/niesportowe)x P(niesportowe)
= 0,572 x 10 ^-5
= 0,0000572
Stąd w końcu otrzymaliśmy nasz klasyfikator, który nadaje „Gra bardzo wyrównana” etykietę Sport, ponieważ jego prawdopodobieństwo jest wysokie i wnioskujemy, że zdanie należy do kategorii Sport.
Zamówienie: Wyjaśnienie modeli uczenia maszynowego
Rodzaje naiwnych klasyfikatorów Bayes
Teraz, gdy zrozumieliśmy, czym jest naiwny klasyfikator Bayesa i widzieliśmy też przykład, zobaczmy, jakie są jego typy:
1. Wielomianowy naiwny klasyfikator Bayesa
Jest to używane głównie w przypadku problemów z klasyfikacją dokumentów, czy dokument należy do kategorii takich jak polityka, sport, technologia itp. Predyktorem używanym przez ten klasyfikator jest częstotliwość słów w dokumencie.
2. Naiwny klasyfikator Bayesa Bernoulliego
Jest to podobne do wielomianowego naiwnego klasyfikatora Bayesa, ale jego predyktorami są zmienne logiczne. Parametry, których używamy do przewidywania zmiennej klasy, przyjmują wartości tylko tak lub nie. Na przykład, czy słowo występuje w tekście, czy nie.
3. Gaussowski klasyfikator Bayesa naiwnego
Gdy predyktory przyjmują stałą wartość, zakładamy, że te wartości są próbkowane z rozkładu Gaussa.
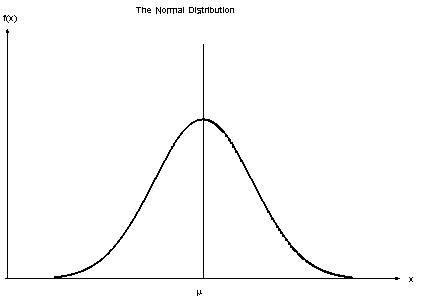
Źródło

Ponieważ wartości obecne w zbiorze danych zmieniają się, formuła prawdopodobieństwa warunkowego zmienia się na:
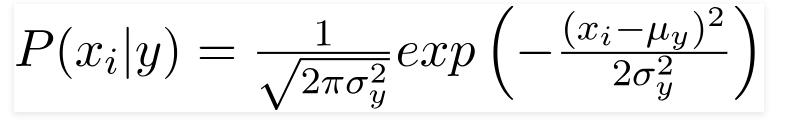
Źródło
Wniosek
Mamy nadzieję, że poprowadzimy Cię po tym, czym jest Naive Bayes Classifier i jak służy do klasyfikowania tekstu. Ta prosta metoda zdziała cuda w problemach klasyfikacji. Niezależnie od tego, czy jesteś ekspertem od uczenia maszynowego, czy nie, możesz zbudować własny klasyfikator Naive Bayes bez poświęcania godzin na kodowanie.
Jeśli chcesz dowiedzieć się więcej, sprawdź wyjątkowe programy Upgrad dotyczące uczenia maszynowego. Nauka klasyfikatorów z upGrad: Rozwiń swoją karierę dzięki wiedzy o uczeniu maszynowym i umiejętnościom uczenia głębokiego. W upGrad Education Pvt. Ltd. , oferujemy program certyfikacji starannie zaprojektowany i nadzorowany przez ekspertów branżowych.
- Ten intensywny 240+ godzinny kurs jest specjalnie zaprojektowany dla pracujących profesjonalistów.
- Będziesz pracować przy ponad pięciu projektach branżowych i studiach przypadków.
- Otrzymasz wsparcie kariery 360 stopni z dedykowanym mentorem sukcesu studenta i mentorem kariery.
- Otrzymasz pomoc w zatrudnieniu i nauczysz się tworzyć dobre CV.
Aplikuj teraz!
