O que é classificador Naive Bayes? [Explicado com Exemplo]
Publicados: 2020-12-28Existem muitos casos em que você está trabalhando em aprendizado de máquina (ML), aprendizado profundo (DL), mineração de dados de um conjunto de dados, programação em Python ou processamento de linguagem natural (NLP) no qual é necessário diferenciar objetos baseados em atributos específicos. Um classificador é um modelo de aprendizado de máquina usado para esse propósito. O classificador Naive Bayes é o cerne desta postagem do blog, que aprenderemos mais adiante.
Teorema de Bayes
O matemático britânico Reverendo Thomas Bayes, o teorema de Bayes é uma fórmula matemática usada para determinar a probabilidade condicional, que é a probabilidade de um resultado ocorrer com base em um resultado anterior.
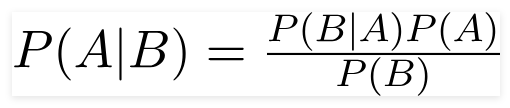
Fonte
Usando esta fórmula, podemos encontrar a probabilidade de A quando B ocorreu.
Aqui,
A é a proposição;

B é a evidência;
P(A) é a probabilidade anterior de proposição;
P(B) é a probabilidade prévia de evidência;
P(A/B) é chamado de posterior e
P(B/A) é chamado de probabilidade.
Por isso,
P osterior = (Probabilidade) (Proposição em probabilidade anterior)
_________________________________
Probabilidade prévia de evidência
Essa fórmula pressupõe que os preditores ou recursos são independentes e a presença de um não afeta o recurso de outro. Por isso, é chamado de 'ingênuo'.
Exemplo de exibição do classificador Naive Bayes
Estamos tomando um exemplo de uma melhor compreensão do tema.
Declaração do problema:
Estamos criando um classificador que mostra se um texto é sobre esportes ou não.
Os dados de treinamento têm cinco frases:
| Frase | Rótulo |
| “Um grande jogo” | Esportes |
| “Acabou a eleição” | Não é esporte |
| “Partida muito limpa” | Esportes |
| “Foi uma eleição apertada” | Não é esporte |
| “Um jogo limpo, mas esquecível” | Esportes |
Aqui, você precisa encontrar a frase 'Um jogo muito próximo' é de qual rótulo?
Naive Bayes, como classificador, calcula a probabilidade da frase “Um jogo muito próximo” ser Esporte com a probabilidade ' Não Esporte'.
Matematicamente, queremos saber P (Sports | a very close game), probabilidade do rótulo Sports na frase “A very close game”.
Agora, o próximo passo é calcular as probabilidades.
Mas antes disso, vamos dar uma olhada em alguns conceitos.
Engenharia de recursos
Precisamos primeiro determinar os recursos a serem usados durante a criação de um modelo de aprendizado de máquina. Características são os pedaços de informação do texto dado ao algoritmo.
No exemplo acima, temos dados como texto. Portanto, precisamos converter o texto em números nos quais realizaremos os cálculos.
Assim, em vez de texto, usaremos as frequências das palavras que ocorrem no texto. As características serão o número dessas palavras.
Aplicando o Teorema de Bayes
Vamos converter a probabilidade a ser calculada usando a contagem da frequência das palavras. Para isso, utilizaremos o Teorema de Bayes e alguns conceitos básicos de probabilidade.
P(A/B) = P(B/A) x P(A)
______________
P(B)
Temos P (Sports | a very close game), e usando o teorema de Bayes, vamos contrariar a probabilidade condicional:
P (esportes/jogo muito disputado) = P(jogo/esportes muito disputados) x P(esportes)
____________________________
P (um jogo muito próximo)
Vamos abandonar o divisor mesmo para ambos os rótulos e comparar
P(jogo muito renhido/Esportes) x P(Esportes)
Com
P(um jogo muito próximo/ Não é esporte) x P(Não é esporte)
Podemos calcular as probabilidades calculando as contagens a frase “Um jogo muito fechado” surge no rótulo 'Esportes'. Para determinar P (um jogo muito próximo | Esportes), divida-o pelo total.
Mas, nos dados de treinamento, 'Um jogo muito próximo' não aparece em lugar algum, então essa probabilidade é zero.
O modelo não terá muita utilidade sem que todas as sentenças que queremos classificar estejam presentes nos dados de treinamento.
Classificador Naive Bayes
Agora vem a parte central aqui, ' Naive'. Cada palavra em uma frase é independente da outra, não estamos olhando para as frases inteiras, mas para palavras isoladas. Saiba mais sobre o classificador naive bayes.
P(um jogo muito próximo) = P(a) x P(muito) x P(próximo) x P(jogo)
Essa presunção é poderosa e útil também. O próximo passo é aplicar:
P(jogo/esporte muito próximo) = P(a/esporte) x P(jogo/esporte) x P(jogo/esporte) x P(jogo/esporte)
Essas palavras individuais aparecem muitas vezes nos dados de treinamento que podemos calcular.
Probabilidade de computação
A etapa final é calcular as probabilidades e ver qual delas é maior .
Primeiro, calculamos a probabilidade a priori dos rótulos: para as sentenças nos dados de treinamento fornecidos. A probabilidade de ser Sports P (Sports) será ⅗, e P (Not Sports) será ⅖.
Ao calcular P (jogo/Esportes), contamos as vezes que a palavra “jogo” aparece no texto de Esportes (aqui 2) dividido pelas palavras em esportes (11).

P(jogo/esportes) = 2/11
Mas, a palavra “perto” não está presente em nenhum texto de Esportes !
Isso significa que P (próximo | Esportes) = 0 e é inconveniente, pois multiplicaremos por outras probabilidades,
P(a/Esporte) x P(muito/Esporte) x 0 x P(jogo/Esporte)
O resultado final será 0 e todo o cálculo será anulado. Mas não é isso que queremos, então procuramos outra forma.
Alisamento de Laplace
Podemos eliminar o problema acima com a suavização de Laplace, onde somaremos 1 para cada contagem; para que nunca seja zero.
Adicionaremos as palavras numéricas possíveis ao divisor e a divisão não será maior que 1.
Neste caso, o conjunto de palavras possíveis é
['a', 'ótimo', 'muito', 'acima', 'isso', 'mas', 'jogo', 'jogo', 'limpo', 'eleição', 'perto', 'o', ' era', 'esquecível'] .
O número possível de palavras é 14; aplicando o alisamento de Laplace,
P(jogo/esportes) = 2+1
___________
11 + 14
Resultado final:
| Palavra | P (palavra | Esportes) | P (palavra | Não Esportes) |
| uma | (2 + 1) ÷ (11 + 14) | (1 + 1) ÷ (9 + 14) |
| muito | (1 + 1) ÷ (11 + 14) | (0 + 1) ÷ (9 + 14) |
| Fechar | (0 + 1) ÷ (11 + 14) | (1 + 1) ÷ (9 + 14) |
| jogos | (2 + 1) ÷ (11 + 14) | (0 + 1) ÷ (9 + 14) |
Agora, multiplicando todas as probabilidades para descobrir qual é maior:
P(a/Esporte) x P(muito/Esporte) x P(jogo/Esporte)x P(jogo/Esporte)x P(Esporte)
= 2,76 x 10 ^-5
= 0,0000276
P(a/não esportivo) x P(muito/não esportivo) x P(jogo/não esportivo)x P(jogo/não esportivo)x P(não esportivo)
= 0,572 x 10 ^-5
= 0,00000572
Assim, temos finalmente nosso classificador que dá a “Um jogo muito fechado” o rótulo Esportes, pois sua probabilidade é alta e inferimos que a sentença pertence à categoria Esportes.
Checkout: modelos de aprendizado de máquina explicados
Tipos de classificador Naive Bayes
Agora que já entendemos o que é um Classificador Naive Bayes e vimos um exemplo também, vamos ver os tipos dele:
1. Classificador Multinomial Naive Bayes
Isso é usado principalmente para problemas de classificação de documentos, se um documento pertence a categorias como política, esportes, tecnologia, etc. O preditor usado por esse classificador é a frequência das palavras no documento.
2. Classificador Bernoulli Naive Bayes
Isso é semelhante ao classificador multinomial Naive Bayes, mas seus preditores são variáveis booleanas. Os parâmetros que usamos para prever a variável de classe assumem apenas os valores sim ou não. Por exemplo, se uma palavra ocorre em um texto ou não.
3. Classificador Gaussiano Naive Bayes
Quando os preditores assumem um valor constante, assumimos que esses valores são amostrados de uma distribuição gaussiana.
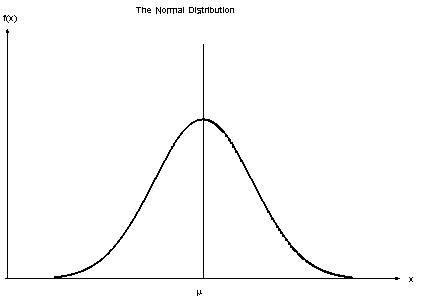
Fonte

Como os valores presentes no conjunto de dados mudam, a fórmula de probabilidade condicional muda para,
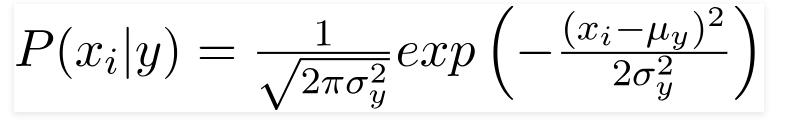
Fonte
Conclusão
Esperamos poder orientá-lo sobre o que é o Naive Bayes Classifier e como ele é usado para classificar o texto. Este método simples faz maravilhas em problemas de classificação. Seja você um especialista em aprendizado de máquina ou não, você pode criar seu próprio classificador Naive Bayes sem gastar horas em codificação.
Se você estiver interessado em aprender mais, confira os programas exclusivos do Upgrad em aprendizado de máquina. Classificadores de aprendizado com upGrad: Dê um impulso à sua carreira com o conhecimento de aprendizado de máquina e suas habilidades de aprendizado profundo. Na upGrad Education Unip. Ltd. , oferecemos um programa de certificação cuidadosamente projetado e orientado por especialistas do setor.
- Este curso intensivo de mais de 240 horas é especialmente projetado para profissionais que trabalham.
- Você trabalhará em mais de cinco projetos do setor e estudos de caso.
- Você receberá suporte de carreira de 360 graus com um mentor de sucesso estudantil dedicado e um mentor de carreira.
- Você receberá assistência para sua colocação e aprenderá a construir um currículo forte.
Aplique agora!
