什么是朴素贝叶斯分类器? 【举例说明】
已发表: 2020-12-28当您从事机器学习 (ML)、深度学习 (DL)、从一组数据中挖掘数据、在 Python 上编程或进行自然语言处理 (NLP) 时,有很多实例需要您区分离散的基于特定属性的对象。 分类器是用于此目的的机器学习模型。 朴素贝叶斯分类器是这篇博文的关键,我们将进一步学习。
贝叶斯定理
英国数学家托马斯·贝叶斯牧师,贝叶斯定理是用来确定条件概率的数学公式,条件概率是一个结果发生的可能性是基于先前的结果。
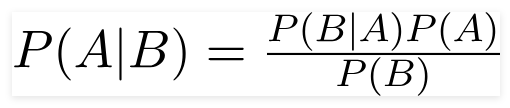
资源
使用这个公式,我们可以找到 B 发生时 A 的概率。
这里,
A是命题;

B是证据;
P(A) 是命题的先验概率;
P(B) 是证据的先验概率;
P(A/B) 称为后验,并且
P(B/A) 称为似然性。
因此,
P osterior = (Likelihood)(先验概率中的命题)
_________________________________
证据先验概率
这个公式假设预测变量或特征是独立的,一个人的存在不会影响另一个人的特征。 因此,它被称为“天真”。
显示朴素贝叶斯分类器的示例
我们正在举一个例子来更好地理解这个话题。
问题陈述:
我们正在创建一个分类器来描述文本是否与运动有关。
训练数据有五句话:
| 句子 | 标签 |
| “一场精彩的比赛” | 运动的 |
| “选举结束了” | 不是运动 |
| “非常干净的比赛” | 运动的 |
| “这是一场势均力敌的选举” | 不是运动 |
| “一个干净但令人难忘的游戏” | 运动的 |
在这里,您需要找到句子“非常接近的游戏”属于哪个标签?
朴素贝叶斯作为分类器计算句子“A very close game” is Sports 的概率为“ Not Sports”。
在数学上,我们想知道 P(体育 | 一场非常接近的比赛),即“非常接近的比赛”句子中标签Sports的概率。
现在,下一步是计算概率。
但在此之前,让我们先来看看一些概念。
特征工程
我们需要首先确定在创建机器学习模型时要使用的功能。 特征是提供给算法的文本中的信息块。
在上面的示例中,我们将数据作为文本。 因此,我们需要将文本转换为我们将执行计算的数字。
因此,我们将使用文本中出现的单词的频率来代替文本。 特征将是这些单词的数量。
应用贝叶斯定理
我们将使用单词频率的计数来转换要计算的概率。 为此,我们将使用贝叶斯定理和一些基本的概率概念。
P(A/B) = P(B/A) x P(A)
______________
前锋(乙)
我们有 P(体育 | 一场非常接近的比赛),并且通过使用贝叶斯定理,我们将抵消条件概率:
P(体育/非常接近的比赛)= P(非常接近的比赛/体育)x P(体育)
____________________________
P(非常接近的游戏)
我们将放弃两个标签的除数相同并进行比较
P(非常接近的比赛/体育)x P(体育)
和
P(非常接近的比赛/非运动)x P(非运动)
我们可以通过计算句子“A very close game”出现在标签“Sports”中的计数来计算概率。 要确定 P(非常接近的游戏 | 体育),请将其除以总数。
但是,在训练数据中,“非常接近的游戏”似乎没有出现在任何地方,所以这个概率为零。
如果我们要分类的每个句子都存在于训练数据中,该模型将没有多大用处。
朴素贝叶斯分类器
现在来到这里的核心部分,“天真”。 句子中的每个单词都是独立的,我们不是在看整个句子,而是看单个单词。 了解有关朴素贝叶斯分类器的更多信息。
P(非常接近的游戏)= P(a)x P(非常)x P(接近)x P(游戏)
这个假设也很强大和有用。 下一步是申请:
P(非常接近的比赛/体育) = P(a/体育) x P(非常/体育) x P(接近/体育) x P(比赛/体育)
这些单独的单词在我们可以计算的训练数据中多次出现。
计算概率
最后一步是计算概率并查看哪个更大。
首先,我们计算标签的先验概率:对于给定训练数据中的句子。 它是Sports P(Sports)的概率为 ⅗,P(Not Sports)的概率为 ⅖。
在计算 P(游戏/体育)时,我们计算“游戏”一词在体育文本(此处为 2)中出现的次数除以体育中的词(11)。

P(游戏/运动)= 2/11
但是,任何体育文本中都没有“接近”这个词!
这意味着 P (close | Sports) = 0 并且不方便,因为我们会将它与其他概率相乘,
P(a/体育) x P(非常/体育) x 0 x P(游戏/体育)
最终结果将为 0,整个计算将无效。 但这不是我们想要的,所以我们寻求其他方式。
拉普拉斯平滑
我们可以通过拉普拉斯平滑消除上述问题,我们将对每个计数加 1; 所以它永远不会是零。
我们将可能的数字词添加到除数,除数不会超过1。
在这种情况下,可能的单词集是
['a', 'great', 'very', 'over', 'it', 'but', 'game', 'match', 'clean', '选举', 'close', 'the', '是','忘记'] 。
可能的字数为 14; 通过应用拉普拉斯平滑,
P(游戏/运动) = 2+1
___________
11 + 14
最终结果:
| 单词 | P(字|体育) | P(字|不是体育) |
| 一种 | (2 + 1) ÷ (11 + 14) | (1 + 1) ÷ (9 + 14) |
| 非常 | (1 + 1) ÷ (11 + 14) | (0 + 1) ÷ (9 + 14) |
| 关闭 | (0 + 1) ÷ (11 + 14) | (1 + 1) ÷ (9 + 14) |
| 游戏 | (2 + 1) ÷ (11 + 14) | (0 + 1) ÷ (9 + 14) |
现在,将所有概率相乘以找出哪个更大:
P(a/体育) x P(非常/体育) x P(游戏/体育)x P(游戏/体育)x P(体育)
= 2.76 x 10 ^-5
= 0.0000276
P(a/非运动)x P(非常/非运动)x P(游戏/非运动)x P(游戏/非运动)x P(非运动)
= 0.572 x 10 ^-5
= 0.00000572
因此,我们最终得到了我们的分类器,它给出了“非常接近的游戏”标签 Sports,因为它的概率很高,我们推断该句子属于 Sports 类别。
结帐:机器学习模型解释
朴素贝叶斯分类器的类型
现在我们已经了解了朴素贝叶斯分类器是什么并且也看过一个例子,让我们看看它的类型:
1.多项朴素贝叶斯分类器
这主要用于文档分类问题,文档是否属于政治、体育、技术等类别。该分类器使用的预测器是文档中单词的频率。
2.伯努利朴素贝叶斯分类器
这类似于多项式朴素贝叶斯分类器,但其预测变量是布尔变量。 我们用来预测类变量的参数只取值是或否。 例如,一个词是否出现在文本中。
3.高斯朴素贝叶斯分类器
当预测变量取一个常数值时,我们假设这些值是从高斯分布中采样的。
资源

由于数据集中存在的值发生变化,条件概率公式变为,
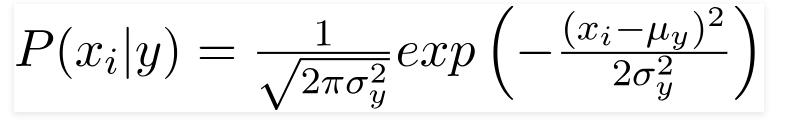
资源
结论
我们希望我们可以指导您了解什么是朴素贝叶斯分类器以及如何使用它对文本进行分类。 这种简单的方法在分类问题中创造了奇迹。 无论您是否是机器学习专家,您都可以构建自己的朴素贝叶斯分类器,而无需花费数小时进行编码。
如果您有兴趣了解更多信息,请查看 Upgrad 在机器学习方面的独家程序。 使用 upGrad 学习分类器:通过机器学习知识和深度学习技能提升您的职业生涯。 在upGrad 教育列兵。 有限公司,我们提供由行业专家精心设计和指导的认证计划。
- 这个 240 多个小时的密集课程专为在职专业人士设计。
- 您将参与五个以上的行业项目和案例研究。
- 您将获得 360 度的职业支持,并配有专门的学生成功导师和职业导师。
- 您将获得安置方面的帮助,并学习建立一份强有力的简历。
现在申请!
