Naive Bayes Sınıflandırıcısı Nedir? [Örnekle Açıklandı]
Yayınlanan: 2020-12-28Makine öğrenimi (ML), derin öğrenme (DL), bir veri kümesinden veri madenciliği, Python'da programlama veya doğal dil işleme (NLP) üzerinde çalışırken, ayrık dilleri ayırt etmeniz gereken pek çok örnek vardır. belirli niteliklere dayalı nesneler. Sınıflandırıcı, bu amaçla kullanılan bir makine öğrenimi modelidir. Naive Bayes Sınıflandırıcısı , daha fazla öğreneceğimiz bu blog yazısının can alıcı noktasıdır.
Bayes teoremi
İngiliz matematikçi Rahip Thomas Bayes, Bayes teoremi, bir sonucun önceki bir sonuca dayalı olarak meydana gelme olasılığı olan koşullu olasılığı belirlemek için kullanılan matematiksel bir formüldür.
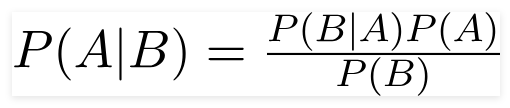
Kaynak
Bu formülü kullanarak, B meydana geldiğinde A'nın olasılığını bulabiliriz.
Burada,
A önermedir;

B kanıttır;
P(A) önermenin önsel olasılığıdır;
P(B) kanıtın önceki olasılığıdır;
P(A/B) arka denir ve
P(B/A) olasılık olarak adlandırılır.
Buradan,
Arka = (Olabilirlik)(Önceki olasılıkla önerme)
_________________________________
Kanıt Ön olasılık
Bu formül, tahmin edicilerin veya özelliklerin bağımsız olduğunu ve birinin varlığının diğerinin özelliğini etkilemediğini varsayar. Bu nedenle, 'naif' olarak adlandırılır.
Naive Bayes Sınıflandırıcısını Gösteren Örnek
Konunun daha iyi anlaşılması için bir örnek alıyoruz.
Sorun bildirimi:
Bir metnin sporla ilgili olup olmadığını gösteren bir sınıflandırıcı oluşturuyoruz.
Eğitim verilerinin beş cümlesi vardır:
| Cümle | Etiket |
| “Harika bir oyun” | Spor Dalları |
| "Seçim bitti" | spor değil |
| “Çok temiz maç” | Spor Dalları |
| “Yakın bir seçimdi” | spor değil |
| “Temiz ama unutulabilir bir oyun” | Spor Dalları |
Burada 'Çok yakın bir oyun' cümlesinin hangi etikete ait olduğunu bulmanız gerekiyor?
Naive Bayes, bir sınıflandırıcı olarak “Çok yakın bir oyun” cümlesinin Spor olma olasılığını ' Spor Değil' olasılığı ile hesaplar.
Matematiksel olarak, P (Spor | çok yakın bir oyun), "Çok yakın bir oyun" cümlesindeki Spor etiketinin olasılığını bilmek istiyoruz .
Şimdi, bir sonraki adım olasılıkları hesaplamak.
Ama ondan önce, bazı kavramlara bir göz atalım.
Özellik Mühendisliği
Bir makine öğrenmesi modeli oluştururken öncelikle kullanılacak özellikleri belirlememiz gerekiyor. Özellikler, metinden algoritmaya verilen bilgi parçalarıdır.
Yukarıdaki örnekte, metin olarak verilerimiz var. Bu nedenle, metni hesaplamaları yapacağımız sayılara dönüştürmemiz gerekiyor.
Bu nedenle metin yerine metinde geçen kelimelerin frekanslarını kullanacağız. Özellikler bu kelimelerin sayısı olacaktır.
Bayes Teoreminin Uygulanması
Sözcüklerin sıklığının sayısını kullanarak hesaplanacak olasılığı dönüştüreceğiz. Bunun için Bayes Teoremi ve bazı temel olasılık kavramlarını kullanacağız.
P(A/B) = P(B/A) x P(A)
______________
P(B)
Elimizde P (Spor | çok yakın bir oyun) var ve Bayes teoremini kullanarak koşullu olasılığı geçersiz kılacağız:
P (spor/ çok yakın bir oyun) = P(çok yakın bir oyun/ spor) x P(spor)
____________________________
P (çok yakın bir oyun)
Hem etiketler hem de karşılaştırma için böleni aynı şekilde bırakacağız.
P(çok yakın bir oyun/ Spor) x P(Spor)
İle birlikte
P(çok yakın bir oyun/ Spor değil) x P(Spor değil)
'Spor' etiketinde ortaya çıkan “Çok yakın bir oyun” cümlesinin sayılarını hesaplayarak olasılıkları hesaplayabiliriz . P'yi (çok yakın bir oyun | Spor) belirlemek için toplama bölün.
Ancak, eğitim verilerinde 'Çok yakın bir oyun' hiçbir yerde görünmüyor, bu nedenle bu olasılık sıfır.
Sınıflandırmak istediğimiz her cümle eğitim verilerinde bulunmadan model pek bir işe yaramaz.
Saf Bayes Sınıflandırıcısı
Şimdi asıl kısım geliyor, ' Naif'. Bir cümledeki her kelime diğerinden bağımsızdır, cümlelerin tamamına değil, tek tek kelimelere bakıyoruz. Saf bayes sınıflandırıcı hakkında daha fazla bilgi edinin.
P(çok yakın bir oyun) = P(a) x P(çok) x P(yakın) x P(oyun)
Bu varsayım da güçlü ve faydalıdır. Bir sonraki adım uygulamaktır:
P(çok yakın bir oyun/Spor) = P(a/Spor) x P(çok/Spor) x P(yakın/Spor) x P(oyun/Spor)
Bu bireysel kelimeler, hesaplayabildiğimiz eğitim verilerinde birçok kez görünür.
Hesaplama Olasılığı
Son adım, olasılıkları hesaplamak ve hangisinin daha büyük olduğuna bakmaktır .
İlk olarak, verilen eğitim verilerindeki cümleler için etiketlerin apriori olasılığını hesaplıyoruz . Bunun Spor P (Spor) olma olasılığı ⅗, P (Spor değil) ise ⅖ olacaktır.
P'yi (oyun/ Spor) hesaplarken, Spor metninde (burada 2) “oyun” kelimesinin geçtiği zamanları spordaki (11) kelimelere bölerek sayarız .

P(oyun/Spor) = 2/11
Ancak, "kapat" kelimesi hiçbir Spor metninde yoktur!
Bu, P (kapat | Spor) = 0 anlamına gelir ve diğer olasılıklarla çarpacağımız için elverişsizdir,
P(a/Spor) x P(çok/Spor) x 0 x P(oyun/Spor)
Sonuç 0 olacak ve tüm hesaplama geçersiz sayılacak. Ama istediğimiz bu değil, bu yüzden başka bir yol arıyoruz.
Laplace Pürüzsüzleştirme
Yukarıdaki sorunu, her sayı için 1 toplayacağımız Laplace yumuşatma ile ortadan kaldırabiliriz; böylece asla sıfır olmaz.
Bölene olası sayı kelimelerini ekleyeceğiz ve bölme 1'den fazla olmayacak.
Bu durumda, olası kelimeler kümesidir
['bir', 'harika', 'çok', 'bitti', 'o', 'ama', 'oyun', 'eşleşme', 'temiz', 'seçim', 'yakın', 'en', ' ', 'unutulabilir'] .
Olası kelime sayısı 14'tür; Laplace yumuşatma uygulayarak,
P(oyun/Spor) = 2+1
__________
11 + 14
Nihai Sonuç:
| Kelime | P (kelime | Spor) | P (kelime | Spor Değil) |
| a | (2 + 1) ÷ (11 + 14) | (1 + 1) ÷ (9 + 14) |
| çok | (1 + 1) ÷ (11 + 14) | (0 + 1) ÷ (9 + 14) |
| kapat | (0 + 1) ÷ (11 + 14) | (1 + 1) ÷ (9 + 14) |
| oyun | (2 + 1) ÷ (11 + 14) | (0 + 1) ÷ (9 + 14) |
Şimdi, hangisinin daha büyük olduğunu bulmak için tüm olasılıkları çarparsak:
P(a/Spor) x P(çok/Spor) x P(oyun/Spor)x P(oyun/Spor)x P(Spor)
= 2,76 x 10 ^-5
= 0.0000276
P(a/Spor Dışı) x P(çok/ Spor Dışı) x P(oyun/ Spor Dışı)x P(oyun/ Spor Dışı)x P(Spor Dışı)
= 0,572 x 10 ^-5
= 0.00000572
Böylece, son olarak, olasılığı yüksek olduğu için Spor etiketini “Çok yakın bir oyun” veren sınıflandırıcımızı elde ettik ve cümlenin Spor kategorisine ait olduğu sonucunu çıkardık.
Ödeme: Açıklanan Makine Öğrenimi Modelleri
Naive Bayes Sınıflandırıcı Türleri
Artık Naive Bayes Sınıflandırıcının ne olduğunu anladığımıza ve bir örneğini de gördüğümüze göre, türlerine bakalım:
1. Çok Terimli Naive Bayes Sınıflandırıcısı
Bir belgenin siyaset, spor, teknoloji vb. kategorilere ait olup olmadığı, çoğunlukla belge sınıflandırma sorunları için kullanılır. Bu sınıflandırıcı tarafından kullanılan tahmin edici, belgedeki kelimelerin sıklığıdır.
2. Bernoulli Naive Bayes Sınıflandırıcısı
Bu, çok terimli Naive Bayes Sınıflandırıcısına benzer, ancak tahmin edicileri boole değişkenleridir. Sınıf değişkenini tahmin etmek için kullandığımız parametreler sadece evet veya hayır değerlerini alır. Örneğin, bir kelimenin bir metinde olup olmadığı.
3. Gauss Saf Bayes Sınıflandırıcısı
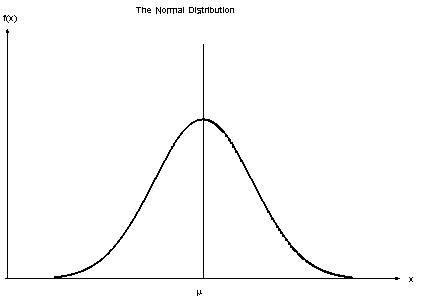
Tahminciler sabit bir değer aldığında, bu değerlerin bir Gauss dağılımından örneklendiğini varsayıyoruz.
Kaynak

Veri kümesinde bulunan değerler değiştiğinden, koşullu olasılık formülü şu şekilde değişir:
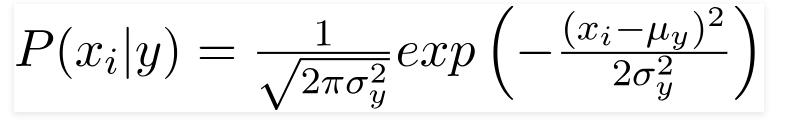
Kaynak
Çözüm
Naive Bayes Sınıflandırıcının ne olduğu ve metni sınıflandırmak için nasıl kullanıldığı konusunda size rehberlik edebileceğimizi umuyoruz . Bu basit yöntem, sınıflandırma problemlerinde harikalar yaratır. Makine Öğrenimi uzmanı olun ya da olmayın, kodlama için saatler harcamadan kendi Naive Bayes Sınıflandırıcınızı oluşturabilirsiniz.
Daha fazlasını öğrenmek istiyorsanız, Upgrad'ın makine öğrenimindeki özel programlarına göz atın. upGrad ile Öğrenme Sınıflandırıcıları: Makine öğrenimi bilgisi ve Derin öğrenme becerilerinizle kariyerinize hız katın. upGrad Education Pvt. Ltd. olarak, endüstri uzmanları tarafından özenle tasarlanmış ve rehberlik edilen bir sertifika programı sunuyoruz.
- Bu yoğun 240+ saatlik kurs, çalışan profesyoneller için özel olarak tasarlanmıştır.
- Beşten fazla endüstri projesi ve vaka çalışması üzerinde çalışacaksınız.
- Özel bir öğrenci başarı danışmanı ve kariyer danışmanı ile 360 derece kariyer desteği alacaksınız.
- Yerleşiminiz için yardım alacak ve güçlü bir özgeçmiş oluşturmayı öğreneceksiniz.
Şimdi Uygula!
