ما هو تصنيف بايز السذاجة؟ [شرح بمثال]
نشرت: 2020-12-28هناك العديد من الحالات التي تعمل فيها على التعلم الآلي (ML) ، أو التعلم العميق (DL) ، أو استخراج البيانات من مجموعة من البيانات ، أو البرمجة على Python ، أو القيام بمعالجة اللغة الطبيعية (NLP) حيث يُطلب منك التمييز المنفصل كائنات على أساس سمات محددة. المصنف هو نموذج التعلم الآلي المستخدم لهذا الغرض. يعتبر Naive Bayes Classifier هو جوهر منشور المدونة هذا والذي سنتعلمه أكثر.
مبرهنة بايز
عالم الرياضيات البريطاني القس توماس بايز ، نظرية بايز هي صيغة رياضية تستخدم لتحديد الاحتمال الشرطي ، وهو احتمال حدوث نتيجة بناءً على نتيجة سابقة.
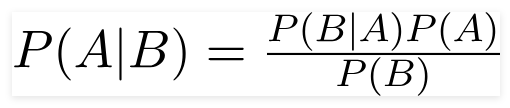
مصدر
باستخدام هذه الصيغة ، يمكننا إيجاد احتمال A عند حدوث B.
هنا،
أ هو الاقتراح.

ب هو الدليل ؛
P (A) هو الاحتمال السابق للقضية ؛
P (B) هو الاحتمال المسبق للأدلة ؛
P (A / B) يسمى الخلفي و
يسمى P (B / A) الاحتمال.
لذلك،
P osterior = (الاحتمالية) (الاقتراح في الاحتمال السابق)
_________________________________
دليل الاحتمال المسبق
تفترض هذه الصيغة أن المتنبئات أو الميزات مستقلة ، وأن حضور الفرد لا يؤثر على ميزة الآخر. ومن ثم يطلق عليه اسم "ساذج".
مثال عرض مصنف بايز ساذج
نحن نأخذ مثالاً على فهم أفضل للموضوع.
عرض المشكلة:
نحن بصدد إنشاء مصنف يصور ما إذا كان النص يتعلق بالرياضة أم لا.
تتكون بيانات التدريب من خمس جمل:
| جملة | ملصق |
| "لعبة رائعة" | رياضات |
| "الانتخابات انتهت" | ليست رياضة |
| "مباراة نظيفة جدا" | رياضات |
| "لقد كانت انتخابات متقاربة" | ليست رياضة |
| "لعبة نظيفة ولكنها منسية" | رياضات |
هنا ، تحتاج إلى العثور على الجملة "لعبة متقاربة جدًا" من أي تسمية؟
يحسب Naive Bayes ، كمصنف ، احتمال الجملة "لعبة متقاربة جدًا" هي الرياضة مع احتمال " ليست رياضة".
رياضياً ، نريد أن نعرف P (الرياضة | لعبة متقاربة للغاية) ، احتمالية تسمية الرياضة في الجملة "لعبة متقاربة جدًا".
الآن ، الخطوة التالية هي حساب الاحتمالات.
لكن قبل ذلك ، دعونا نلقي نظرة على بعض المفاهيم.
هندسة الخصائص
نحتاج أولاً إلى تحديد الميزات التي يجب استخدامها أثناء إنشاء نموذج التعلم الآلي. الميزات هي أجزاء من المعلومات من النص المعطى للخوارزمية.
في المثال أعلاه ، لدينا بيانات كنص. لذلك ، نحتاج إلى تحويل النص إلى أرقام نقوم فيها بإجراء العمليات الحسابية.
ومن ثم ، فبدلاً من النص ، سنستخدم ترددات الكلمات الواردة في النص. ستكون الميزات هي عدد هذه الكلمات.
تطبيق نظرية بايز
سنقوم بتحويل الاحتمال المراد حسابه باستخدام عدد مرات تكرار الكلمات. لهذا ، سوف نستخدم نظرية بايز وبعض المفاهيم الأساسية للاحتمال.
الفوسفور (أ / ب) = الفوسفور (ب / أ) × ف (أ)
______________
ف (ب)
لدينا P (رياضة | لعبة متقاربة جدًا) ، وباستخدام نظرية بايز ، سنبطل الاحتمال الشرطي:
P (رياضة / لعبة قريبة جدًا) = P (لعبة قريبة جدًا / رياضة) x P (رياضة)
____________________________
P (لعبة متقاربة للغاية)
سنتخلى عن القاسم نفسه لكل من التسميات والمقارنة
ف (مباراة قريبة جدا / رياضة) × ف (رياضة)
مع
P (لعبة قريبة جدًا / ليست رياضية) × P (ليست رياضية)
يمكننا حساب الاحتمالات من خلال حساب التعداد ، تظهر الجملة "لعبة متقاربة جدًا" في التسمية "الرياضة". لتحديد P (لعبة متقاربة جدًا | رياضة) ، قسّمها على الإجمالي.
ولكن ، في بيانات التدريب ، لا تبدو "لعبة متقاربة جدًا" في أي مكان ، لذا فإن هذا الاحتمال هو صفر.
لن يكون للنموذج فائدة كبيرة بدون وجود كل جملة نريد تصنيفها في بيانات التدريب.
مصنف بايز ساذج
الآن يأتي الجزء الأساسي هنا ، " ساذج". كل كلمة في جملة مستقلة عن الأخرى ، نحن لا ننظر إلى الجمل بأكملها ، ولكن في الكلمات المفردة. تعرف على المزيد حول مصنف بايز ساذج.
P (لعبة قريبة جدًا) = P (a) x P (جدًا) x P (قريب) x P (لعبة)
هذا الافتراض قوي ومفيد أيضًا. الخطوة التالية هي التقديم:
P (لعبة قريبة جدًا / رياضة) = P (a / Sports) x P (جدًا / رياضي) x P (قريب / رياضي) x P (لعبة / رياضة)
تظهر هذه الكلمات الفردية عدة مرات في بيانات التدريب التي يمكننا حسابها.
احتمالية الحوسبة
الخطوة النهائية هي حساب الاحتمالات والنظر في أي الاحتمالات أكبر .
أولاً ، نحسب الاحتمال المسبق للتسميات: للجمل في بيانات التدريب المحددة. احتمالية أن تكون رياضة P (رياضة) ستكون ⅗ و P (ليست رياضة) ستكون ⅖.
أثناء حساب P (لعبة / رياضة) ، نحسب مرات ظهور كلمة "game" في النص الرياضي (هنا 2) مقسومًا على الكلمات في الرياضة (11).

ف (لعبة / رياضة) = 2/11
لكن كلمة "إغلاق" غير موجودة في أي نص رياضي !
هذا يعني أن P (close | Sports) = 0 وهو غير مريح لأننا سنضربه مع الاحتمالات الأخرى ،
ف (أ / رياضة) × ف (للغاية / رياضية) × 0 × ف (لعبة / رياضة)
ستكون النتيجة النهائية 0 ، وسيتم إلغاء العملية الحسابية بالكامل. لكن هذا ليس ما نريده ، لذلك نسعى بطريقة أخرى.
تنعيم لابلاس
يمكننا القضاء على المشكلة المذكورة أعلاه مع تجانس لابلاس ، حيث سنلخص 1 في كل عدد ؛ بحيث لا يكون صفرًا أبدًا.
سنضيف عدد الكلمات المحتملة للمقسوم عليه ، ولن تكون القسمة أكثر من 1.
في هذه الحالة ، تكون مجموعة الكلمات الممكنة
['a'، 'great'، 'very'، 'over'، 'it'، 'but'، 'game'، 'match'، 'clean'، 'الانتخابات'، 'close'، 'the'، ' كان "،" يمكن نسيانه "] .
العدد المحتمل للكلمات هو 14 ؛ من خلال تطبيق تجانس لابلاس ،
ف (لعبة / رياضة) = 2 + 1
___________
11 + 14
الحصيلة النهائية:
| كلمة | ف (كلمة | رياضة) | P (كلمة | ليست رياضة) |
| أ | (2 + 1) (11 + 14) | (1 + 1) (9 + 14) |
| جدا | (1 + 1) (11 + 14) | (0 + 1) (9 + 14) |
| قريب | (0 + 1) (11 + 14) | (1 + 1) (9 + 14) |
| لعبه | (2 + 1) (11 + 14) | (0 + 1) (9 + 14) |
الآن ، نضرب كل الاحتمالات لإيجاد أيهما أكبر:
P (a / Sports) x P (very / Sports) x P (لعبة / رياضة) x P (لعبة / رياضة) x P (رياضة)
= 2.76 × 10 ^ -5
= 0.0000276
P (أ / غير رياضي) × P (جدًا / غير رياضي) × P (لعبة / غير رياضية) × P (لعبة / غير رياضية) × P (غير رياضية)
= 0.572 × 10 ^ -5
= 0.00000572
ومن ثم ، فقد حصلنا أخيرًا على المصنف الذي يعطي "لعبة متقاربة جدًا" التسمية الرياضية نظرًا لأن احتمالها مرتفع ونستنتج أن الجملة تنتمي إلى فئة الرياضة.
الخروج: شرح نماذج التعلم الآلي
أنواع مصنف بايز ساذج
الآن بعد أن فهمنا ما هو مصنف Naive Bayes وقد رأينا مثالًا أيضًا ، دعنا نرى أنواعه:
1. مصنف بايز ساذج متعدد الحدود
يستخدم هذا في الغالب لمشاكل تصنيف المستندات ، سواء كان المستند ينتمي إلى فئات مثل السياسة ، والرياضة ، والتكنولوجيا ، وما إلى ذلك. المتنبئ الذي يستخدمه هذا المصنف هو تكرار الكلمات في المستند.
2. مصنف Bernoulli Naive Bayes
هذا مشابه لمصنف Naive Bayes متعدد الحدود ، لكن تنبئه عبارة عن متغيرات منطقية. تأخذ المعلمات التي نستخدمها للتنبؤ بمتغير الفئة القيم بنعم أو لا فقط. على سبيل المثال ، ما إذا كانت الكلمة تظهر في النص أم لا.
3. مصنف بايز غاوسي ساذج
عندما تأخذ المتنبئات قيمة ثابتة ، نفترض أن هذه القيم مأخوذة من توزيع غاوسي.
مصدر

نظرًا لأن القيم الموجودة في مجموعة البيانات تتغير ، تتغير صيغة الاحتمال الشرطي إلى ،
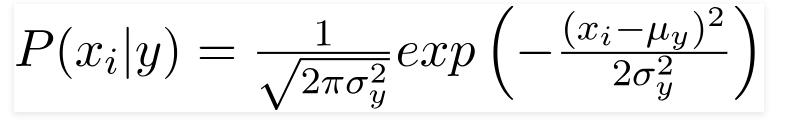
مصدر
خاتمة
نأمل أن نتمكن من إرشادك إلى ما هو Naive Bayes Classifier وكيف يتم استخدامه لتصنيف النص. هذه الطريقة البسيطة تعمل العجائب في مشاكل التصنيف. سواء كنت خبيرًا في تعلم الآلة أم لا ، يمكنك إنشاء برنامج Naive Bayes Classifier الخاص بك دون قضاء ساعات في البرمجة.
إذا كنت مهتمًا بمعرفة المزيد ، فتحقق من برامج Upgrad الحصرية في التعلم الآلي. تصنيفات التعلم مع upGrad: أعط دفعة لحياتك المهنية من خلال معرفة التعلم الآلي ومهارات التعلم العميق الخاصة بك. في upGrad Education Pvt. المحدودة ، نحن نقدم برنامج شهادة مصمم بعناية وإرشاد من قبل خبراء الصناعة.
- تم تصميم هذه الدورة التدريبية المكثفة التي تزيد عن 240 ساعة خصيصًا للمهنيين العاملين.
- ستعمل على أكثر من خمسة مشاريع صناعية ودراسات حالة.
- ستتلقى دعمًا مهنيًا بزاوية 360 درجة مع مرشد نجاح للطلاب وموجه وظيفي.
- سوف تحصل على مساعدة في التنسيب الخاص بك وتتعلم كيفية بناء سيرة ذاتية قوية.
قدم الآن!
