¿Qué es el clasificador Naive Bayes? [Explicado con ejemplo]
Publicado: 2020-12-28Hay tantos casos en los que trabaja en aprendizaje automático (ML), aprendizaje profundo (DL), extracción de datos de un conjunto de datos, programación en Python o procesamiento de lenguaje natural (NLP) en los que debe diferenciar discretos objetos basados en atributos específicos. Un clasificador es un modelo de aprendizaje automático utilizado para este propósito. El clasificador Naive Bayes es el quid de esta publicación de blog que aprenderemos más.
Teorema de Bayes
El reverendo matemático británico Thomas Bayes, el teorema de Bayes es una fórmula matemática utilizada para determinar la probabilidad condicional, que es la probabilidad de que ocurra un resultado en función de un resultado anterior.
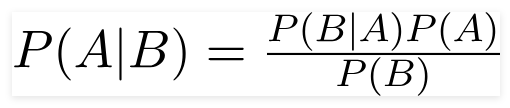
Fuente
Usando esta fórmula, podemos encontrar la probabilidad de A cuando B ha ocurrido.
Aquí,
A es la proposición;

B es la evidencia;
P(A) es la probabilidad previa de la proposición;
P(B) es la probabilidad previa de evidencia;
P(A/B) se llama posterior y
P(B/A) se llama probabilidad.
Por eso,
P osterior = (Verosimilitud)(Proposición en probabilidad previa)
_________________________________
Evidencia Probabilidad previa
Esta fórmula asume que los predictores o funciones son independientes y que la presencia de uno no afecta la función de otro. Por lo tanto, se llama 'ingenuo'.
Ejemplo de visualización del clasificador Naive Bayes
Estamos tomando un ejemplo de una mejor comprensión del tema.
Planteamiento del problema:
Estamos creando un clasificador que muestra si un texto es sobre deportes o no.
Los datos de entrenamiento tienen cinco oraciones:
| Oración | Etiqueta |
| “Un gran juego” | Deportes |
| “Se acabaron las elecciones” | no deportes |
| “Partido muy limpio” | Deportes |
| “Fue una elección reñida” | no deportes |
| “Un juego limpio pero olvidable” | Deportes |
Aquí, ¿de qué etiqueta es la oración 'Un juego muy cerrado'?
Naive Bayes, como clasificador, calcula la probabilidad de la oración "Un juego muy cerrado" es Deportes con la probabilidad " No Deportes".
Matemáticamente, queremos saber P (Deportes | un juego muy cerrado), probabilidad de la etiqueta Deportes en la oración “Un juego muy cerrado”.
Ahora, el siguiente paso es calcular las probabilidades.
Pero antes de eso, echemos un vistazo a algunos conceptos.
Ingeniería de funciones
Primero debemos determinar las funciones que se usarán durante la creación de un modelo de aprendizaje automático. Las características son los fragmentos de información del texto proporcionado al algoritmo.
En el ejemplo anterior, tenemos datos como texto. Entonces, necesitamos convertir el texto en números en los que realizaremos los cálculos.
Por lo tanto, en lugar de texto, usaremos las frecuencias de las palabras que aparecen en el texto. Las características serán el número de estas palabras.
Aplicando el Teorema de Bayes
Convertiremos la probabilidad que se calculará utilizando el conteo de la frecuencia de las palabras. Para ello, utilizaremos el Teorema de Bayes y algunos conceptos básicos de probabilidad.
P(A/B) = P(B/A) x P(A)
______________
P(B)
Tenemos P (Deportes | un juego muy cerrado), y usando el teorema de Bayes, anularemos la probabilidad condicional:
P (deportes/un juego muy cerrado) = P(un juego muy cerrado/deportes) x P(deportes)
____________________________
P (un juego muy cerrado)
Abandonaremos el mismo divisor para ambas etiquetas y compararemos
P(un juego muy cerrado/ Deportes) x P(Deportes)
Con
P(un juego muy cerrado/ No Deportes) x P(No Deportes)
Podemos calcular las probabilidades calculando los conteos. La oración "Un juego muy cerrado" surge en la etiqueta 'Deportes'. Para determinar P (un juego muy cerrado | Deportes), divídalo por el total.
Pero, en los datos de entrenamiento, 'Un juego muy cerrado' no aparece en ninguna parte, por lo que esta probabilidad es cero.
El modelo no será de mucha utilidad si cada oración que queremos clasificar está presente en los datos de entrenamiento.
Clasificador bayesiano ingenuo
Ahora viene la parte central aquí, ' Ingenuo'. Cada palabra en una oración es independiente de las demás, no estamos viendo oraciones completas, sino palabras sueltas. Obtenga más información sobre el clasificador naive bayes.
P(un juego muy cerrado) = P(a) x P(muy) x P(cerrado) x P(juego)
Esta presunción es poderosa y útil también. El siguiente paso es aplicar:
P(un juego/Deportes muy cerrado) = P(un/Deportes) x P(muy/Deportes) x P(cerca/Deportes) x P(juego/Deportes)
Estas palabras individuales aparecen muchas veces en los datos de entrenamiento que podemos calcular.
Computación de probabilidad
El paso final es calcular las probabilidades y ver cuál es mayor .
Primero, calculamos la probabilidad a priori de las etiquetas: para las oraciones en los datos de entrenamiento dados. La probabilidad de que sea Deportes P (Deportes) será ⅗, y P (No Deportes) será ⅖.
Mientras calculamos P (juego/Deportes), contamos las veces que aparece la palabra “juego” en el texto de Deportes (aquí 2) dividido por las palabras en deportes (11).

P(juego/Deportes) = 2/11
¡Pero la palabra “cerrar” no está presente en ningún texto deportivo !
Esto significa que P (cerrar | Deportes) = 0 y es un inconveniente ya que lo multiplicaremos con otras probabilidades,
P(a/Deportes) x P(muy/Deportes) x 0 x P(juego/Deportes)
El resultado final será 0 y se anulará todo el cálculo. Pero esto no es lo que queremos, así que buscamos otra forma.
Suavizado de Laplace
Podemos eliminar el problema anterior con el suavizado de Laplace, donde sumaremos 1 para cada conteo; para que nunca sea cero.
Agregaremos las palabras numéricas posibles al divisor, y la división no será más de 1.
En este caso, el conjunto de palabras posibles son
['un', 'genial', 'muy', 'sobre', 'eso', 'pero', 'juego', 'partido', 'limpio', 'elección', 'cerrar', 'el', ' era', 'olvidable'] .
El número posible de palabras es 14; mediante la aplicación de suavizado de Laplace,
P(juego/Deportes) = 2+1
___________
11 + 14
Resultado final:
| Palabra | P (palabra | Deportes) | P (palabra | No deportes) |
| a | (2 + 1) ÷ (11 + 14) | (1 + 1) ÷ (9 + 14) |
| muy | (1 + 1) ÷ (11 + 14) | (0 + 1) ÷ (9 + 14) |
| cerrar | (0 + 1) ÷ (11 + 14) | (1 + 1) ÷ (9 + 14) |
| juego | (2 + 1) ÷ (11 + 14) | (0 + 1) ÷ (9 + 14) |
Ahora, multiplicando todas las probabilidades para encontrar cuál es mayor:
P(a/Deportes) x P(muy/Deportes) x P(juego/Deportes)x P(juego/Deportes)x P(Deportes)
= 2,76 x 10^-5
= 0.0000276
P(a/No Deportes) x P(muy/ No Deportes) x P(juego/ No Deportes)x P(juego/ No Deportes)x P(No Deportes)
= 0.572x10^-5
= 0.00000572
Por lo tanto, finalmente tenemos nuestro clasificador que le da a "Un juego muy cerrado" la etiqueta Deportes ya que su probabilidad es alta e inferimos que la oración pertenece a la categoría Deportes.
Pago: Explicación de los modelos de aprendizaje automático
Tipos de clasificador Naive Bayes
Ahora que hemos entendido qué es un clasificador Naive Bayes y también hemos visto un ejemplo, veamos sus tipos:
1. Clasificador Naive Bayes multinomial
Esto se usa principalmente para problemas de clasificación de documentos, ya sea que un documento pertenezca a categorías como política, deportes, tecnología, etc. El predictor utilizado por este clasificador es la frecuencia de las palabras en el documento.
2. Clasificador Bernoulli Naive Bayes
Esto es similar al clasificador Naive Bayes multinomial, pero sus predictores son variables booleanas. Los parámetros que usamos para predecir la variable de clase toman los valores sí o no solamente. Por ejemplo, si una palabra aparece en un texto o no.
3. Clasificador Gaussiano Naive Bayes
Cuando los predictores toman un valor constante, asumimos que estos valores se muestrean a partir de una distribución gaussiana.
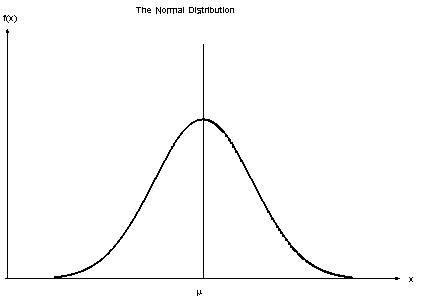
Fuente

Dado que los valores presentes en el conjunto de datos cambian, la fórmula de probabilidad condicional cambia a,
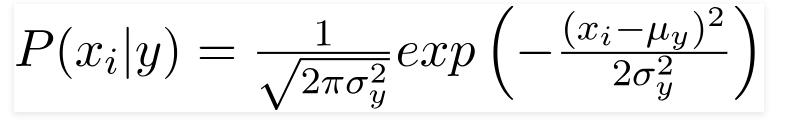
Fuente
Conclusión
Esperamos poder guiarlo sobre qué es Naive Bayes Classifier y cómo se usa para clasificar texto. Este método simple funciona de maravilla en problemas de clasificación. Ya sea que sea un experto en aprendizaje automático o no, puede crear su propio clasificador Naive Bayes sin tener que dedicar horas a la codificación.
Si está interesado en obtener más información, consulte los programas exclusivos de Upgrad en aprendizaje automático. Clasificadores de aprendizaje con upGrad: dé un impulso a su carrera con el conocimiento del aprendizaje automático y sus habilidades de aprendizaje profundo. En upGrad Education Pvt. Ltd. , ofrecemos un programa de certificación cuidadosamente diseñado y asesorado por expertos de la industria.
- Este curso intensivo de más de 240 horas está especialmente diseñado para profesionales que trabajan.
- Trabajará en más de cinco proyectos de la industria y estudios de casos.
- Recibirá apoyo profesional de 360 grados con un mentor dedicado al éxito de los estudiantes y un mentor profesional.
- Obtendrá asistencia para su colocación y aprenderá a crear un currículum sólido.
¡Aplica ya!
