Что такое наивный байесовский классификатор? [Поясняется на примере]
Опубликовано: 2020-12-28Есть так много случаев, когда вы работаете над машинным обучением (ML), глубоким обучением (DL), извлечением данных из набора данных, программированием на Python или обработкой естественного языка (NLP), в которых вам необходимо различать дискретные объекты по определенным признакам. Классификатор — это модель машинного обучения, используемая для этой цели. Наивный байесовский классификатор — суть этого поста в блоге, который мы изучим дальше.
Теорема Байеса
Теорема Байеса , британский математик преподобный Томас Байес, представляет собой математическую формулу, используемую для определения условной вероятности, которая представляет собой вероятность того, что результат произойдет на основе предыдущего результата.
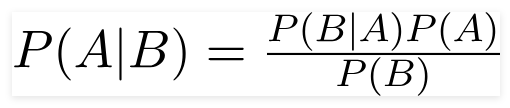
Источник
Используя эту формулу, мы можем найти вероятность A, когда произошло B.
Здесь,
А — предложение;

Б — свидетельство;
P(A) — априорная вероятность предложения;
P(B) — априорная вероятность свидетельства;
P(A/B) называется апостериорным и
P(B/A) называется вероятностью.
Следовательно,
P osterior = (вероятность) (предложение в априорной вероятности)
_________________________________
Доказательство Априорная вероятность
Эта формула предполагает, что предикторы или признаки независимы, и присутствие одного не влияет на признак другого. Поэтому его называют «наивным».
Пример отображения наивного байесовского классификатора
Берем пример лучшего понимания темы.
Постановка задачи:
Мы создаем классификатор, который показывает, о спорте текст или нет.
Учебные данные состоят из пяти предложений:
| Предложение | Этикетка |
| «Отличная игра» | Спортивный |
| «Выборы закончились» | Не спорт |
| «Очень чистый матч» | Спортивный |
| «Это были близкие выборы» | Не спорт |
| «Чистая, но забываемая игра» | Спортивный |
Здесь вам нужно найти предложение «Очень близкая игра» какого лейбла?
Наивный Байес, как классификатор, вычисляет вероятность того, что предложение «Очень близкая игра» является Спортом с вероятностью « Не Спорт».
Математически мы хотим знать P (Спорт | очень близкая игра), вероятность ярлыка « Спорт» в предложении «Очень близкая игра».
Теперь следующий шаг — вычисление вероятностей.
Но перед этим давайте взглянем на некоторые концепции.
Разработка функций
Сначала нам нужно определить функции, которые будут использоваться при создании модели машинного обучения. Особенности — это фрагменты информации из текста, переданные алгоритму.
В приведенном выше примере у нас есть данные в виде текста. Итак, нам нужно преобразовать текст в числа, в которых мы будем производить вычисления.
Следовательно, вместо текста мы будем использовать частоты слов, встречающихся в тексте. Особенностями будет количество этих слов.
Применение теоремы Байеса
Мы преобразуем вероятность, которую нужно рассчитать, используя подсчет частоты слов. Для этого воспользуемся теоремой Байеса и некоторыми основными понятиями вероятности.
Р(А/В) = Р(В/А) х Р(А)
______________
П(Б)
У нас есть P (Спорт | очень близкая игра), и, используя теорему Байеса, мы отменим условную вероятность:
P (спортивная/очень напряженная игра) = P(очень напряженная игра/спортивная) x P(спортивная)
____________________________
P (очень близкая игра)
Откажемся от делителя одинакового для обеих меток и сравним
P(очень близкая игра/Спорт) x P(Спорт)
С участием
P(очень близкая игра/не спорт) x P(не спорт)
Мы можем рассчитать вероятности, подсчитав количество предложений «Очень близкая игра» в метке «Спорт». Чтобы определить P (очень близкая игра | Спорт), разделите его на тотал.
Но в тренировочных данных «Очень близкая игра» нигде не встречается, поэтому эта вероятность равна нулю.
Модель будет бесполезна, если каждое предложение, которое мы хотим классифицировать, не будет присутствовать в обучающих данных.
Наивный байесовский классификатор
Теперь идет основная часть здесь, « Наивный». Каждое слово в предложении не зависит от другого, мы смотрим не на все предложение целиком, а на отдельные слова. Узнайте больше о наивном байесовском классификаторе.
P(очень близкая игра) = P(a) x P(очень) x P(близкая игра) x P(игра)
Эта презумпция также мощна и полезна. Следующим шагом является применение:
P(очень близкая игра/Спорт) = P(a/Спорт) x P(очень/Спорт) x P(близкая/Спорт) x P(игра/Спорт)
Эти отдельные слова появляются много раз в обучающих данных, которые мы можем вычислить.
Вычисление вероятности
Завершающим этапом является подсчет вероятностей и определение того, какая из них больше .
Во-первых, мы вычисляем априорную вероятность меток: для предложений в заданных обучающих данных. Вероятность того, что это спорт P (спорт), будет ⅗, а P (не спорт) будет ⅖.
При вычислении P (game/Sports) мы подсчитываем количество раз, когда слово «game» встречается в тексте Sports (здесь 2), деленное на количество слов в Sports (11).

P(игра/спорт) = 2/11
Но слова «близко» нет ни в одном спортивном тексте!
Это означает P (close | Sports) = 0 и неудобно, так как мы будем умножать его на другие вероятности,
P(a/Спорт) x P(очень/Спорт) x 0 x P(игра/Спорт)
Конечным результатом будет 0, и весь расчет будет аннулирован. Но это не то, чего мы хотим, поэтому ищем другой путь.
Сглаживание Лапласа
Мы можем устранить вышеуказанную проблему с помощью сглаживания Лапласа, где мы будем суммировать 1 на каждый счет; чтобы он никогда не был равен нулю.
Мы добавим к делителю возможное число слов, и деление не будет больше 1.
В этом случае множество возможных слов равно
['а', 'отлично', 'очень', 'за', 'это', 'но', 'игра', 'совпадение', 'чисто', 'выборы', 'близко', 'то', ' был', 'забытый'] .
Возможное количество слов 14; применяя сглаживание Лапласа,
P(игра/спорт) = 2+1
___________
11 + 14
Окончательный результат:
| Слово | Р (слово | Спорт) | P (слово | Не спорт) |
| а | (2 + 1) ÷ (11 + 14) | (1 + 1) ÷ (9 + 14) |
| очень | (1 + 1) ÷ (11 + 14) | (0 + 1) ÷ (9 + 14) |
| близко | (0 + 1) ÷ (11 + 14) | (1 + 1) ÷ (9 + 14) |
| игра | (2 + 1) ÷ (11 + 14) | (0 + 1) ÷ (9 + 14) |
Теперь перемножаем все вероятности, чтобы найти, какая из них больше:
P(a/Спорт) x P(очень/Спорт) x P(игры/Спорт) x P(игры/Спорт) x P(Спорт)
= 2,76 х 10^-5
= 0,0000276
P(a/не спорт) x P(очень/не спорт) x P(игры/не спорт) x P(игры/не спорт) x P(не спорт)
= 0,572 х 10^-5
= 0,00000572
Следовательно, мы, наконец, получили наш классификатор, который дает «Очень близкой игре» метку «Спорт», поскольку ее вероятность высока, и мы делаем вывод, что предложение относится к категории «Спорт».
Оформление заказа: объяснение моделей машинного обучения
Типы наивного байесовского классификатора
Теперь, когда мы поняли, что такое наивный байесовский классификатор, а также увидели пример, давайте посмотрим на его типы:
1. Полиномиальный наивный байесовский классификатор
Это используется в основном для задач классификации документов, независимо от того, принадлежит ли документ к таким категориям, как политика, спорт, технологии и т. д. Предиктором, используемым этим классификатором, является частота слов в документе.
2. Наивный байесовский классификатор Бернулли
Это похоже на полиномиальный наивный байесовский классификатор, но его предикторы являются булевыми переменными. Параметры, которые мы используем для прогнозирования переменной класса, принимают только значения «да» или «нет». Например, встречается ли слово в тексте или нет.
3. Гауссовский наивный байесовский классификатор
Когда предикторы принимают постоянное значение, мы предполагаем, что эти значения взяты из распределения Гаусса.
Источник

Поскольку значения, присутствующие в наборе данных, меняются, формула условной вероятности изменяется на
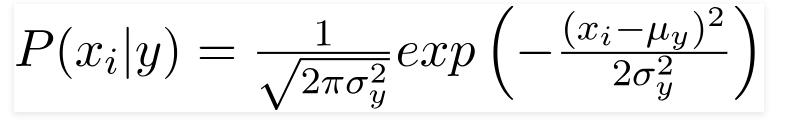
Источник
Заключение
Мы надеемся, что смогли рассказать вам, что такое наивный байесовский классификатор и как он используется для классификации текста. Этот простой метод творит чудеса в задачах классификации. Являетесь ли вы экспертом по машинному обучению или нет, вы можете создать свой собственный наивный байесовский классификатор , не тратя часы на кодирование.
Если вы хотите узнать больше, ознакомьтесь с эксклюзивными программами Upgrad по машинному обучению. Изучение классификаторов с upGrad: ускорьте свою карьеру благодаря знаниям в области машинного обучения и своим навыкам глубокого обучения. В upGrad Education Pvt. Ltd. , мы предлагаем программу сертификации, тщательно разработанную и курируемую отраслевыми экспертами.
- Этот интенсивный курс продолжительностью более 240 часов специально разработан для работающих профессионалов.
- Вы будете работать над более чем пятью отраслевыми проектами и кейсами.
- Вы получите всестороннюю поддержку карьеры с помощью преданного наставника по успеху студентов и наставника по карьере.
- Вы получите помощь в трудоустройстве и научитесь составлять сильное резюме.
Применить сейчас!
