ลักษณนาม Naive Bayes คืออะไร? [อธิบายด้วยตัวอย่าง]
เผยแพร่แล้ว: 2020-12-28มีหลายกรณีเมื่อคุณทำงานกับการเรียนรู้ของเครื่อง (ML), การเรียนรู้เชิงลึก (DL), การขุดข้อมูลจากชุดข้อมูล, การเขียนโปรแกรมบน Python หรือการประมวลผลภาษาธรรมชาติ (NLP) ที่คุณต้องแยกความแตกต่าง วัตถุตามคุณลักษณะเฉพาะ ลักษณนามคือโมเดลแมชชีนเลิร์นนิงที่ใช้เพื่อจุดประสงค์ Naive Bayes Classifier เป็น หัวใจสำคัญของโพสต์บล็อกนี้ ซึ่งเราจะเรียนรู้เพิ่มเติม
ทฤษฎีบทของเบย์
นักคณิตศาสตร์ชาวอังกฤษ สาธุคุณ Thomas Bayes ทฤษฎีบทของ Bayes เป็นสูตรทางคณิตศาสตร์ที่ใช้ในการกำหนดความน่าจะเป็นแบบมีเงื่อนไข ซึ่งเป็นความน่าจะเป็นของผลลัพธ์ที่เกิดขึ้นจากผลลัพธ์ก่อนหน้า
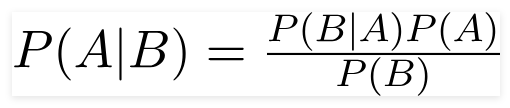
แหล่งที่มา
โดยใช้สูตรนี้ เราสามารถหาความน่าจะเป็นของ A เมื่อเกิด B
ที่นี่,
A คือข้อเสนอ;

ข. เป็นหลักฐาน;
P(A) คือความน่าจะเป็นก่อนหน้าของข้อเสนอ
P(B) คือความน่าจะเป็นของหลักฐานก่อนหน้า
P(A/B) เรียกว่าส่วนหลังและ
P(B/A) เรียกว่า ความน่าจะเป็น
เพราะฉะนั้น,
P osterior = (ความน่าจะเป็น)(ข้อเสนอในความน่าจะเป็นก่อนหน้า)
________________________________________________
หลักฐานความน่าจะเป็นก่อนหน้า
สูตรนี้อนุมานว่าตัวทำนายหรือคุณลักษณะเป็นอิสระ และการแสดงตนไม่มีผลต่อคุณลักษณะของผู้อื่น ดังนั้นจึงเรียกว่า 'ไร้เดียงสา'
ตัวอย่างการแสดง Naive Bayes Classifier
เรากำลังยกตัวอย่างความเข้าใจในหัวข้อนี้มากขึ้น
คำชี้แจงปัญหา:
เรากำลังสร้างตัวแยกประเภทที่แสดงให้เห็นว่าข้อความเกี่ยวกับกีฬาหรือไม่
ข้อมูลการฝึกอบรมมีห้าประโยค:
| ประโยค | ฉลาก |
| “เกมที่ยอดเยี่ยม” | กีฬา |
| “การเลือกตั้งจบลงแล้ว” | ไม่ใช่กีฬา |
| “การแข่งขันที่สะอาดมาก” | กีฬา |
| “เป็นการเลือกตั้งที่ใกล้ชิด” | ไม่ใช่กีฬา |
| “เกมที่สะอาด แต่น่าจดจำ” | กีฬา |
ที่นี่คุณต้องค้นหาประโยค 'A very close game' เป็นป้ายกำกับใด
Naive Bayes เป็นตัวแยกประเภท คำนวณความน่าจะเป็นของประโยค "เกมที่ใกล้มาก" คือกีฬาที่มีความน่าจะเป็น ' ไม่ใช่กีฬา'
ทางคณิตศาสตร์เราต้องการทราบ P (Sports | a very close game) ความน่าจะเป็นของป้าย Sports ในประโยค "A very close game"
ขั้นตอนต่อไปคือการคำนวณความน่าจะเป็น
แต่ก่อนหน้านั้นเรามาดูแนวคิดกันก่อนดีกว่า
วิศวกรรมคุณลักษณะ
ก่อนอื่นเราต้องกำหนดคุณสมบัติที่จะใช้ในขณะที่สร้างแบบจำลองการเรียนรู้ของเครื่อง คุณลักษณะเป็นส่วนของข้อมูลจากข้อความที่กำหนดให้กับอัลกอริทึม
ในตัวอย่างข้างต้น เรามีข้อมูลเป็นข้อความ ดังนั้น เราจำเป็นต้องแปลงข้อความเป็นตัวเลขที่เราจะทำการคำนวณ
ดังนั้น แทนที่จะใช้ข้อความ เราจะใช้ความถี่ของคำที่เกิดขึ้นในข้อความ คุณสมบัติจะเป็นจำนวนคำเหล่านี้
การใช้ทฤษฎีบทเบย์
เราจะแปลงความน่าจะเป็นที่จะคำนวณโดยใช้การนับความถี่ของคำ สำหรับสิ่งนี้ เราจะใช้ทฤษฎีบทของเบย์และแนวคิดพื้นฐานบางประการของความน่าจะเป็น
P(A/B) = P(B/A) x P(A)
_____________
พี(บี)
เรามี P (กีฬา | เกมที่ใกล้มาก) และโดยใช้ทฤษฎีบทเบย์ เราจะแก้ไขความน่าจะเป็นแบบมีเงื่อนไข:
P (กีฬา/ เกมที่ใกล้มาก) = P (เกม/ กีฬาที่ใกล้เคียงมาก) x P (กีฬา)
__________________________________________
P (เกมที่ใกล้มาก)
เราจะละทิ้งตัวหารเหมือนกันสำหรับทั้งป้ายกำกับและเปรียบเทียบ
P(เกมที่ใกล้เคียงมาก/ กีฬา) x P(กีฬา)
กับ
P(เกมที่ใกล้เคียงมาก/ ไม่ใช่กีฬา) x P(ไม่ใช่กีฬา)
เราสามารถคำนวณความน่าจะเป็นโดยการคำนวณการนับประโยค "เกมที่ใกล้มาก" ปรากฏในป้ายกำกับ 'กีฬา' เพื่อหา P (เกมที่ใกล้มาก | กีฬา) ให้หารด้วยผลรวม
แต่ในข้อมูลการฝึก 'เกมที่ใกล้มาก' ดูเหมือนจะไม่มีที่ไหนเลย ความน่าจะเป็นนี้จึงเป็นศูนย์
โมเดลจะไม่มีประโยชน์มากนักหากไม่มีทุกประโยคที่เราต้องการจัดประเภทมีอยู่ในข้อมูลการฝึกอบรม
Naive Bayes ลักษณนาม
มาถึงส่วนหลักที่นี่ ' ไร้เดียงสา' ทุกคำในประโยคเป็นอิสระจากคำอื่นๆ เราไม่ได้ดูทั้งประโยค แต่ดูที่คำเดียว เรียนรู้เพิ่มเติมเกี่ยวกับลักษณนามที่ไร้เดียงสา
P(เกมที่ใกล้มาก) = P(a) x P(มาก) x P(ใกล้มาก) x P(เกม)
ข้อสันนิษฐานนี้มีประสิทธิภาพและมีประโยชน์เช่นกัน ขั้นตอนต่อไปคือการสมัคร:
P(เกม/กีฬาที่ใกล้เคียงมาก) = P(a/กีฬา) x P(เกม/กีฬามาก) x P(ใกล้/กีฬา) x P(เกม/กีฬา)
คำแต่ละคำเหล่านี้ปรากฏขึ้นหลายครั้งในข้อมูลการฝึกอบรมที่เราสามารถคำนวณได้
ความน่าจะเป็นในการคำนวณ
ขั้นตอนสุดท้ายคือการคำนวณความน่าจะเป็นและดูว่าอันไหนมีค่ามากกว่า กัน
อันดับแรก เราคำนวณ ความ น่าจะเป็นของป้ายกำกับ: สำหรับประโยคในข้อมูลการฝึกที่กำหนด ความน่าจะเป็นที่จะเป็น Sports P (Sports) จะเป็น ⅗ และ P (ไม่ใช่ Sports) จะเป็น ⅖
ขณะคำนวณ P (เกม/ กีฬา) เราจะนับครั้งที่คำว่า "เกม" ปรากฏใน ข้อความ กีฬา (ในที่นี้ 2) หารด้วยคำใน กีฬา (11)

P(เกม/กีฬา) = 2/11
แต่ไม่มีคำว่า "ปิด" ใน ข้อความ กีฬา !
นี่หมายความว่า P (ปิด | กีฬา) = 0 และไม่สะดวกเพราะเราจะคูณด้วยความน่าจะเป็นอื่น
P(a/กีฬา) x P(มาก/กีฬา) x 0 x P(เกม/กีฬา)
ผลลัพธ์สุดท้ายจะเป็น 0 และการคำนวณทั้งหมดจะเป็นโมฆะ แต่นี่ไม่ใช่สิ่งที่เราต้องการ ดังนั้นเราจึงหาวิธีอื่น
ลาเพลส สมูทติ้ง
เราสามารถขจัดปัญหาข้างต้นด้วยการปรับ Laplace ให้เรียบ โดยเราจะรวม 1 ทุกการนับ เพื่อที่จะไม่เป็นศูนย์
เราจะเพิ่มจำนวนคำที่เป็นไปได้ลงในตัวหาร และการหารจะต้องไม่เกิน 1
ในกรณีนี้ ชุดคำที่เป็นไปได้คือ
['a', 'great', 'very', 'over', 'it', 'but', 'game', 'match', 'clean', 'election', 'close', 'the', ' เป็น', 'ลืมไม่ได้'] .
จำนวนคำที่เป็นไปได้คือ 14; โดยทาลาปลาซ สมูทติ้ง
P(เกม/กีฬา) = 2+1
___________
11 + 14
ผลลัพธ์สุดท้าย:
| คำ | P (คำ | กีฬา) | P (คำ | ไม่ใช่กีฬา) |
| เอ | (2 + 1) ÷ (11 + 14) | (1 + 1) ÷ (9 + 14) |
| มาก | (1 + 1) ÷ (11 + 14) | (0 + 1) ÷ (9 + 14) |
| ปิด | (0 + 1) ÷ (11 + 14) | (1 + 1) ÷ (9 + 14) |
| เกม | (2 + 1) ÷ (11 + 14) | (0 + 1) ÷ (9 + 14) |
ทีนี้ คูณความน่าจะเป็นทั้งหมดเพื่อหาว่าอันไหนที่มากกว่า:
P(a/กีฬา) x P(มาก/กีฬา) x P(เกม/กีฬา)x P(เกม/กีฬา) x P(กีฬา)
= 2.76 x 10 ^-5
= 0.0000276
P(a/Non Sports) x P(มาก/ Non Sports) x P(เกม/ Non Sports)x P(เกม/ Non Sports)x P(Non Sports)
= 0.572 x 10 ^-5
= 0.00000572
ดังนั้นในที่สุด เราก็ได้ตัวจำแนกประเภทที่ให้คำว่า "เกมที่ใกล้เคียง" กับกีฬา เนื่องจากมีความเป็นไปได้สูง และเราอนุมานได้ว่าประโยคนั้นอยู่ในหมวดกีฬา
ชำระเงิน: อธิบายแบบจำลองการเรียนรู้ของเครื่อง
ประเภทของลักษณนามไร้เดียงสา
ตอนนี้เราเข้าใจแล้วว่า Naive Bayes Classifier คืออะไรและได้เห็นตัวอย่างแล้ว มาดูประเภทของมันกันดีกว่า:
1. Multinomial Naive Bayes ลักษณนาม
ส่วนใหญ่จะใช้สำหรับปัญหาการจัดหมวดหมู่เอกสาร ไม่ว่าจะเป็นเอกสารที่อยู่ในหมวดหมู่ต่างๆ เช่น การเมือง กีฬา เทคโนโลยี ฯลฯ ตัวทำนายที่ใช้โดยตัวแยกประเภทนี้คือความถี่ของคำในเอกสาร
2. ลักษณนามเบอร์นูลลีไร้เดียงสา
สิ่งนี้คล้ายกับ multinomial Naive Bayes Classifier แต่ตัวทำนายเป็นตัวแปรบูลีน พารามิเตอร์ที่เราใช้ทำนายตัวแปรคลาสใช้ค่าใช่หรือไม่ใช่เท่านั้น ตัวอย่างเช่น ไม่ว่าคำนั้นจะปรากฏในข้อความหรือไม่
3. Gaussian Naive Bayes ลักษณนาม
เมื่อตัวทำนายใช้ค่าคงที่ เราคิดว่าค่าเหล่านี้มาจากการแจกแจงแบบเกาส์เซียน
แหล่งที่มา

เนื่องจากค่าที่มีอยู่ในชุดข้อมูลเปลี่ยนไป สูตรความน่าจะเป็นแบบมีเงื่อนไขจะเปลี่ยนเป็น
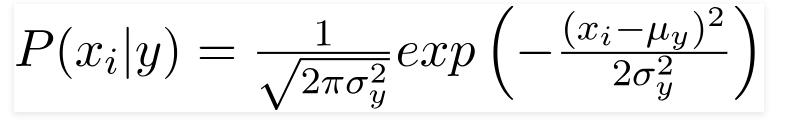
แหล่งที่มา
บทสรุป
เราหวังว่าเราจะสามารถแนะนำคุณว่า Naive Bayes Classifier คืออะไรและใช้เพื่อจำแนกข้อความอย่างไร วิธีง่ายๆ นี้ใช้ได้ผลดีในปัญหาการจำแนกประเภท ไม่ว่าคุณจะเป็นผู้เชี่ยวชาญด้านแมชชีนเลิร์นนิงหรือไม่ก็ตาม คุณสามารถสร้าง Naive Bayes Classifier ของคุณเอง ได้โดยไม่ต้องใช้เวลาหลายชั่วโมงในการเขียนโค้ด
หากคุณสนใจที่จะเรียนรู้เพิ่มเติม โปรดดูโปรแกรมพิเศษของ Upgrad ในการเรียนรู้ของเครื่อง ตัวแยกประเภทการเรียนรู้ด้วย upGrad: ส่งเสริมอาชีพของคุณด้วยความรู้ด้านแมชชีนเลิร์นนิงและทักษะการเรียนรู้เชิงลึกของคุณ ที่ upGrad Education Pvt. Ltd. เราขอเสนอโปรแกรมการรับรองที่ออกแบบและให้คำปรึกษาอย่างพิถีพิถันโดยผู้เชี่ยวชาญในอุตสาหกรรม
- หลักสูตรเข้มข้น 240+ ชั่วโมงนี้ออกแบบมาเป็นพิเศษสำหรับมืออาชีพด้านการทำงาน
- คุณจะทำงานมากกว่าห้าโครงการอุตสาหกรรมและกรณีศึกษา
- คุณจะได้รับการสนับสนุนด้านอาชีพแบบ 360 องศาพร้อมที่ปรึกษาด้านความสำเร็จของนักเรียนและที่ปรึกษาด้านอาชีพโดยเฉพาะ
- คุณจะได้รับความช่วยเหลือสำหรับตำแหน่งของคุณและเรียนรู้ที่จะสร้างเรซูเม่ที่แข็งแกร่ง
ลงทะเบียนเลย!
