나이브 베이즈 분류기란 무엇입니까? [예시 설명]
게시 됨: 2020-12-28머신 러닝(ML), 딥 러닝(DL), 데이터 집합에서 데이터 마이닝, Python 프로그래밍 또는 자연어 처리(NLP)를 수행할 때 이산을 구별해야 하는 경우가 너무 많습니다. 특정 속성을 기반으로 하는 개체. 분류기는 이를 위해 사용되는 기계 학습 모델입니다. Naive Bayes Classifier 는 이 블로그 게시물의 핵심이며 앞으로 더 배우게 될 것입니다.
베이즈의 정리
영국 수학자 Thomas Bayes, Bayes 의 정리는 조건부 확률을 결정하는 데 사용되는 수학 공식입니다. 조건부 확률은 이전 결과를 기반으로 결과가 발생할 가능성입니다.
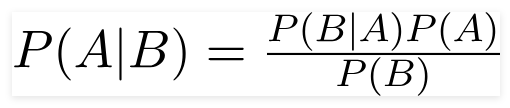
원천
이 공식을 사용하여 B가 발생했을 때 A가 발생할 확률을 찾을 수 있습니다.
여기,
A는 명제입니다.

B는 증거입니다.
P(A)는 명제의 사전 확률입니다.
P(B)는 증거의 사전 확률입니다.
P(A/B)는 후부라고 하며
P(B/A)를 우도라고 합니다.
따라서,
후방 = (우도)(사전 확률의 명제)
_________________________________
증거 사전 확률
이 공식은 예측 변수 또는 기능이 독립적이며 자신의 존재가 다른 사람의 기능에 영향을 미치지 않는다고 가정합니다. 그래서 '순진한'이라고 합니다.
나이브 베이즈 분류기를 표시하는 예
우리는 주제에 대한 더 나은 이해의 예를 취하고 있습니다.
문제 설명:
텍스트가 스포츠에 관한 것인지 여부를 나타내는 분류기를 만들고 있습니다.
훈련 데이터에는 5개의 문장이 있습니다.
| 문장 | 상표 |
| “훌륭한 게임” | 스포츠 |
| "선거 끝났다"… | 스포츠 아님 |
| “매우 깨끗한 경기” | 스포츠 |
| “거의 선거였다” | 스포츠 아님 |
| “깨끗하지만 잊혀지지 않는 게임” | 스포츠 |
여기서 '매우 가까운 게임'이라는 문장을 찾아야 하는 레이블은 무엇입니까?
Naive Bayes는 분류기로서 "A very close game" 문장이 Sports일 확률을 ' Not Sports'로 계산합니다.
수학적으로 우리는 P(스포츠 | 매우 가까운 경기), "매우 가까운 경기"라는 문장에서 스포츠 라는 레이블의 확률을 알고 싶습니다.
이제 다음 단계는 확률을 계산하는 것입니다.
그러나 그 전에 몇 가지 개념을 살펴보겠습니다.
피처 엔지니어링
먼저 기계 학습 모델을 생성하는 동안 사용할 기능을 결정해야 합니다. 기능은 알고리즘에 제공된 텍스트의 정보 덩어리입니다.
위의 예에서 우리는 데이터를 텍스트로 가지고 있습니다. 따라서 텍스트를 계산을 수행할 숫자로 변환해야 합니다.
따라서 텍스트 대신 텍스트에서 발생하는 단어의 빈도를 사용합니다. 기능은 이러한 단어의 수입니다.
베이즈 정리 적용하기
단어의 빈도수를 이용하여 계산할 확률을 환산해 보겠습니다. 이를 위해 Bayes의 정리와 확률의 몇 가지 기본 개념을 사용할 것입니다.
P(A/B) = P(B/A) x P(A)
______________
피(나)
우리는 P(스포츠 | 매우 가까운 게임)를 가지고 있으며 베이즈 정리를 사용하여 조건부 확률을 반박할 것입니다.
P(스포츠/매우 가까운 게임) = P(매우 가까운 게임/스포츠) x P(스포츠)
____________________________
P (매우 가까운 게임)
두 레이블에 대해 동일한 제수를 포기하고 비교합니다.
P(매우 가까운 게임/스포츠) x P(스포츠)
와 함께
P(매우 가까운 게임/스포츠 아님) x P(스포츠 아님)
'스포츠'라는 레이블에 나오는 "매우 가까운 게임" 이라는 문장의 개수를 계산하여 확률을 계산할 수 있습니다 . P(매우 가까운 게임 | 스포츠)를 결정하려면 총계로 나눕니다.
그러나 훈련 데이터에서 '매우 근접한 게임'은 어디에도 보이지 않으므로 이 확률은 0입니다.
분류하려는 모든 문장이 훈련 데이터에 존재하지 않으면 모델은 별로 유용하지 않을 것입니다.
나이브 베이즈 분류기
이제 핵심 부분인 ' 나이브'가 나옵니다. 문장의 모든 단어는 다른 단어와 독립적입니다. 우리는 전체 문장을 보는 것이 아니라 단일 단어를 봅니다. 나이브 베이 분류기에 대해 자세히 알아보십시오.
P(매우 가까운 게임) = P(a) x P(매우) x P(가까운) x P(게임)
이 가정은 강력하고 유용합니다. 다음 단계는 적용하는 것입니다.
P(매우 가까운 게임/스포츠) = P(a/스포츠) x P(매우/스포츠) x P(가까운/스포츠) x P(게임/스포츠)
이러한 개별 단어는 우리가 계산할 수 있는 훈련 데이터에 여러 번 나타납니다.
확률 계산
마무리 단계는 확률을 계산하고 어느 것이 더 큰지 확인하는 것입니다 .
먼저 주어진 훈련 데이터의 문장에 대해 레이블 의 선험적 확률을 계산합니다. 그것이 스포츠 P(스포츠)일 확률은 ⅗이고 P(스포츠가 아님)는 ⅖입니다.
P(게임/스포츠)를 계산할 때 스포츠 텍스트(여기서는 2) 에 "게임"이라는 단어가 나타난 횟수를 스포츠 (11)의 단어로 나눈 값을 계산합니다.

P(게임/스포츠) = 2/11
그러나 "닫기"라는 단어는 스포츠 텍스트에 없습니다!
이것은 P(닫기 | 스포츠) = 0을 의미하며 다른 확률과 곱하기 때문에 불편합니다.
P(a/스포츠) x P(매우/스포츠) x 0 x P(게임/스포츠)
최종 결과는 0이 되며 전체 계산이 무효화됩니다. 그러나 이것은 우리가 원하는 것이 아니므로 다른 방법을 모색합니다.
라플라스 평활화
Laplace 평활화로 위의 문제를 제거할 수 있습니다. 여기에서 모든 개수에 대해 1을 합산합니다. 절대 0이 되지 않도록.
가능한 숫자 단어를 제수에 추가하고 나눗셈은 1보다 크지 않습니다.
이 경우 가능한 단어 집합은 다음과 같습니다.
['아', '대단하다', '매우', '이상', '그것', '하지만', '게임', '매치', '청결', '선거', '마무리', 'the', ' ', '잊을 수 있다'] .
가능한 단어 수는 14입니다. 라플라스 평활화를 적용하여,
P(게임/스포츠) = 2+1
__________
11 + 14
최종 결과:
| 단어 | P(단어 | 스포츠) | P(단어 | 스포츠 아님) |
| ㅏ | (2 + 1) ÷ (11 + 14) | (1 + 1) ÷ (9 + 14) |
| 매우 | (1 + 1) ÷ (11 + 14) | (0 + 1) ÷ (9 + 14) |
| 닫기 | (0 + 1) ÷ (11 + 14) | (1 + 1) ÷ (9 + 14) |
| 게임 | (2 + 1) ÷ (11 + 14) | (0 + 1) ÷ (9 + 14) |
이제 더 큰 것을 찾기 위해 모든 확률을 곱합니다.
P(a/스포츠) x P(매우/스포츠) x P(게임/스포츠)x P(게임/스포츠)x P(스포츠)
= 2.76 x 10 ^-5
= 0.0000276
P(a/비스포츠) x P(매우/비스포츠) x P(게임/비스포츠)x P(게임/비스포츠)x P(비스포츠)
= 0.572 x 10 ^-5
= 0.00000572
따라서 우리는 가능성이 높기 때문에 "매우 가까운 게임"이라는 레이블을 제공하는 분류기를 마침내 얻었고 문장이 스포츠 범주에 속한다고 추론합니다.
체크아웃: 기계 학습 모델 설명
나이브 베이즈 분류기의 유형
이제 Naive Bayes Classifier가 무엇인지 이해하고 예제도 보았으므로 유형을 살펴보겠습니다.
1. 다항 나이브 베이즈 분류기
이것은 문서가 정치, 스포츠, 기술 등과 같은 범주에 속하는지 여부에 관계없이 문서 분류 문제에 주로 사용됩니다. 이 분류자가 사용하는 예측자는 문서에 있는 단어의 빈도입니다.
2. 베르누이 나이브 베이즈 분류기
이것은 다항 Naive Bayes Classifier 와 유사 하지만 예측 변수는 부울 변수입니다. 클래스 변수를 예측하는 데 사용하는 매개변수는 yes 또는 no 값만 사용합니다. 예를 들어, 단어가 텍스트에서 발생하는지 여부.
3. 가우시안 나이브 베이즈 분류기
예측 변수가 상수 값을 취하는 경우 이러한 값이 가우스 분포에서 샘플링된 것으로 가정합니다.
원천

데이터 세트에 있는 값이 변경되기 때문에 조건부 확률 공식은 다음과 같이 변경됩니다.
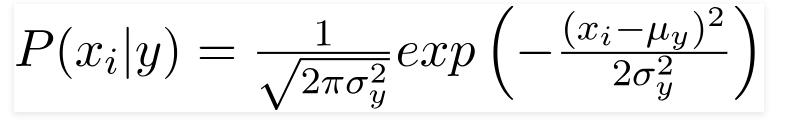
원천
결론
Naive Bayes Classifier 가 무엇이며 텍스트를 분류하는 데 사용되는 방법 에 대해 안내해 드릴 수 있기를 바랍니다 . 이 간단한 방법은 분류 문제에서 훌륭하게 작동합니다. 기계 학습 전문가이든 아니든 코딩에 시간을 들이지 않고도 자신만의 Naive Bayes 분류기 를 구축할 수 있습니다.
더 자세히 알아보려면 Upgrad의 기계 학습 독점 프로그램을 확인하십시오. upGrad로 분류기 학습: 머신 러닝에 대한 지식과 딥 러닝 기술로 경력을 향상시키십시오. upGrad Education Pvt에서 Ltd. , 우리는 업계 전문가가 신중하게 설계하고 멘토링한 인증 프로그램을 제공합니다.
- 이 집중 240시간 이상의 과정은 전문직 종사자를 위해 특별히 고안되었습니다.
- 5개 이상의 산업 프로젝트와 사례 연구에서 일하게 됩니다.
- 헌신적인 학생 성공 멘토와 진로 멘토와 함께 360도 진로 지원을 받게 됩니다.
- 배치에 대한 도움을 받고 강력한 이력서를 작성하는 방법을 배웁니다.
지금 신청하세요!
