使用開源工具的科學計算指南

從歷史上看，計算科學在很大程度上僅限於研究科學家和博士生的領域。 然而，這些年來——也許更大的軟件社區不知道——我們科學計算的蛋頭們一直在悄悄地編譯協作開源庫來處理絕大多數繁重的工作。 結果是，現在實現數學模型比以往任何時候都更容易，雖然該領域可能還沒有為大規模消費做好準備，但成功實施的門檻已經大大降低。 從頭開始開發新的計算代碼庫是一項艱鉅的任務，通常以數年為單位，但這些開源科學計算項目使得運行可訪問的示例成為可能，以相對快速地利用這些計算能力。

由於科學計算的目的是為自然界中存在的真實係統提供科學見解，因此該學科代表了使計算機軟件接近現實的前沿。 為了使軟件能夠以非常高的精度和分辨率模擬現實世界，必須調用複雜的微分數學，這需要在大學、國家實驗室或企業研發部門之外很少發現的知識。 最重要的是，當嘗試使用零和一的離散語言來描述現實世界的連續、無窮小的結構時，會出現重大的數值挑戰。 為了呈現計算上易於處理且呈現有意義結果的算法，需要進行仔細的數值轉換的詳盡努力。 換句話說，科學計算是重任。

科學計算的開源工具

我個人特別喜歡 FEniCS 項目，將它用於我的論文工作，並將證明我在選擇它作為本教程的代碼示例時的偏見。 （還有其他非常高質量的項目，例如 DUNE，也可以使用。）

FEniCS 自稱是“一個為自動化科學計算開發創新概念和工具的合作項目，特別關注通過有限元方法自動求解微分方程。” 這是一個強大的庫，用於解決大量問題和科學計算應用程序。 它的貢獻者包括 Simula 研究實驗室、劍橋大學、芝加哥大學、貝勒大學和 KTH 皇家理工學院，在過去十年中，他們共同將其打造為寶貴的資源（參見 FEniCS 代碼群）。

令人驚訝的是 FEniCS 庫為我們提供了多少努力。 要了解該項目所涵蓋主題的驚人深度和廣度，可以查看他們的開源教科書，其中第 21 章甚至比較了解決不可壓縮流的各種有限元方案。

該項目在幕後為我們集成了大量的開源科學計算庫，這些庫可能會感興趣或直接使用。 這些包括，沒有特別的順序，FEniCS項目調用的項目：

• PETSc：一套數據結構和例程，用於由偏微分方程建模的科學應用的可擴展（並行）解決方案。
• Trilinos 項目：一套強大的算法和技術，用於求解線性和非線性方程，由桑迪亞國家實驗室開發。
• uBLAS：“一個 C++ 模板類庫，為密集、壓縮和稀疏矩陣提供 BLAS 1、2、3 級功能，以及許多用於線性代數的數值算法。”
• GMP：任意精度算術的免費庫，對有符號整數、有理數和浮點數進行操作。
• UMFPACK：一組用於求解非對稱稀疏線性系統的例程，Ax=b，使用非對稱 MultiFrontal 方法。
• ParMETIS：一個基於 MPI 的並行庫，它實現了用於劃分非結構化圖、網格和計算稀疏矩陣的填充減少排序的各種算法。
• NumPy：使用 Python 進行科學計算的基礎包。
• CGAL：C++ 庫形式的高效可靠的幾何算法。
• SCOTCH：用於順序和並行圖形分區、靜態映射和聚類、順序網格和超圖分區以及順序和並行稀疏矩陣塊排序的軟件包和庫。
• MPI：由學術界和工業界的一組研究人員設計的標準化和便攜式消息傳遞系統，可在各種並行計算機上運行。
• VTK：用於 3D 計算機圖形、圖像處理和可視化的開源、免費提供的軟件系統。
• SLEPc：用於解決並行計算機上的大規模稀疏特徵值問題的軟件庫。

這個集成到項目中的外部包列表讓我們了解它的繼承能力。 例如，對 MPI 的集成支持允許在計算集群環境中跨遠程工作人員進行擴展（即，此代碼將在超級計算機或您的筆記本電腦上運行）。

值得注意的是，除了科學計算之外，還有許多應用程序可以利用這些項目，包括金融建模、圖像處理、優化問題，甚至可能是視頻遊戲。 例如，可以創建一個視頻遊戲，該遊戲使用其中一些開源算法和技術來解決二維流體流動問題，例如玩家將與之交互的洋流/河流（也許嘗試和用不同的風和水流航行船）。

示例應用程序：利用開源進行科學計算

在這裡，我將嘗試通過展示如何在這些開源庫之一（在本例中為 FEniCS 項目）中開發和實現基本的計算流體動力學方案來了解開發數值模型所涉及的內容。 FEnICS 提供 Python 和 C++ 的 API。 對於這個例子，我們將使用他們的 Python API。

我們將討論一些相當技術性的內容，但目標只是讓我們了解開發這種科學計算代碼需要什麼，以及今天的開源工具為我們做了多少繁瑣的工作。 在此過程中，希望我們能幫助揭開復雜的科學計算世界的神秘面紗。 （請注意，提供了一個附錄，其中詳細介紹了對這些詳細程度感興趣的人的所有數學和科學基礎。）

免責聲明：對於那些在科學計算軟件和應用程序方面很少或沒有背景的讀者，本示例的部分內容可能會讓您感覺如下：

如果是這樣，請不要絕望。 這裡的主要內容是現有開源項目可以在多大程度上簡化許多這些任務。

考慮到這一點，讓我們從查看不可壓縮 Navier-Stokes 的 FEnICS 演示開始。 此演示模擬流經 L 形彎管（如管道）的不可壓縮流體的壓力和速度。

鏈接的演示頁面上的描述對運行代碼的必要步驟進行了出色、簡潔的設置，我鼓勵您快速查看其中涉及的內容。 總而言之，該演示將求解不可壓縮流動方程通過彎曲處的速度和壓力。 該演示對隨時間流動的流體進行了簡短的模擬，並對結果進行了動畫處理。 這是通過設置表示管道空間的網格，並使用有限元方法對網格上每個點的速度和壓力進行數值求解來實現的。 然後我們遍歷時間，更新速度和壓力場，再次使用我們可以使用的方程。

該演示按原樣運行良好，但我們將對其稍作修改。 該演示使用 Chorin 拆分，但我們將使用受 Kim 和 Moin 啟發的略有不同的方法，我們希望這種方法更穩定。 這只需要我們改變用於近似對流項和粘性項的方程，但要做到這一點，我們需要存儲前一個時間步的速度場，並在更新方程中添加兩個附加項，這將使用之前的信息以獲得更準確的數值近似。

所以讓我們做出這個改變。 首先，我們在設置中添加一個新的Function對象。 這是一個表示抽像數學函數的對象，例如向量或標量場。 我們稱它為un1它將存儲先前的速度場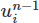在我們的函數空間V上。

 ... # Create functions (three distinct vector fields and a scalar field) un1 = Function(V) # the previous time step's velocity field we are adding u0 = Function(V) # the current velocity field u1 = Function(V) # the next velocity field (what's being solved for) p1 = Function(Q) # the next pressure field (what's being solved for) ...

接下來，我們需要在模擬的每個步驟中更改“暫定速度”的更新方式。 該字段表示忽略壓力時下一個時間步長的近似速度（此時壓力尚不清楚）。 這是我們用更新的 Kim 和 Moin 分數步法替換 Chorin 分裂法的地方。 換句話說，我們將更改字段F1的表達式：

代替：

 # Tentative velocity field (a first prediction of what the next velocity field is) # for the Chorin style split # F1 = change in the velocity field + # convective term + # diffusive term - # body force term F1 = (1/k)*inner(u - u0, v)*dx + \ inner(grad(u0)*u0, v)*dx + \ nu*inner(grad(u), grad(v))*dx - \ inner(f, v)*dx

和：

 # Tentative velocity field (a first prediction of what the next velocity field is) # for the Kim and Moin style split # F1 = change in the velocity field + # convective term + # diffusive term - # body force term F1 = (1/k)*inner(u - u0, v)*dx + \ (3.0/2.0) * inner(grad(u0)*u0, v)*dx - (1.0/2.0) * inner(grad(un1)*un1, v)*dx + \ (nu/2.0)*inner(grad(u+u0), grad(v))*dx - \ inner(f, v)*dx

以便演示現在使用我們更新的方法在使用F1時求解中間速度場。

最後，確保我們在每個迭代步驟結束時更新先前的速度場un1

 ... # Move to next time step un1.assign(u0) # copy the current velocity field into the previous velocity field u0.assign(u1) # copy the next velocity field into the current velocity field ...

因此，以下是我們的 FEniCS CFD 演示的完整代碼，其中包括我們的更改：

 """This demo program solves the incompressible Navier-Stokes equations on an L-shaped domain using Kim and Moin's fractional step method.""" # Begin demo from dolfin import * # Print log messages only from the root process in parallel parameters["std_out_all_processes"] = False; # Load mesh from file mesh = Mesh("lshape.xml.gz") # Define function spaces (P2-P1) V = VectorFunctionSpace(mesh, "Lagrange", 2) Q = FunctionSpace(mesh, "Lagrange", 1) # Define trial and test functions u = TrialFunction(V) p = TrialFunction(Q) v = TestFunction(V) q = TestFunction(Q) # Set parameter values dt = 0.01 T = 3 nu = 0.01 # Define time-dependent pressure boundary condition p_in = Expression("sin(3.0*t)", t=0.0) # Define boundary conditions noslip = DirichletBC(V, (0, 0), "on_boundary && \ (x[0] < DOLFIN_EPS | x[1] < DOLFIN_EPS | \ (x[0] > 0.5 - DOLFIN_EPS && x[1] > 0.5 - DOLFIN_EPS))") inflow = DirichletBC(Q, p_in, "x[1] > 1.0 - DOLFIN_EPS") outflow = DirichletBC(Q, 0, "x[0] > 1.0 - DOLFIN_EPS") bcu = [noslip] bcp = [inflow, outflow] # Create functions un1 = Function(V) u0 = Function(V) u1 = Function(V) p1 = Function(Q) # Define coefficients k = Constant(dt) f = Constant((0, 0)) # Tentative velocity field (a first prediction of what the next velocity field is) # for the Kim and Moin style split # F1 = change in the velocity field + # convective term + # diffusive term - # body force term F1 = (1/k)*inner(u - u0, v)*dx + \ (3.0/2.0) * inner(grad(u0)*u0, v)*dx - (1.0/2.0) * inner(grad(un1)*un1, v)*dx + \ (nu/2.0)*inner(grad(u+u0), grad(v))*dx - \ inner(f, v)*dx a1 = lhs(F1) L1 = rhs(F1) # Pressure update a2 = inner(grad(p), grad(q))*dx L2 = -(1/k)*div(u1)*q*dx # Velocity update a3 = inner(u, v)*dx L3 = inner(u1, v)*dx - k*inner(grad(p1), v)*dx # Assemble matrices A1 = assemble(a1) A2 = assemble(a2) A3 = assemble(a3) # Use amg preconditioner if available prec = "amg" if has_krylov_solver_preconditioner("amg") else "default" # Create files for storing solution ufile = File("results/velocity.pvd") pfile = File("results/pressure.pvd") # Time-stepping t = dt while t < T + DOLFIN_EPS: # Update pressure boundary condition p_in.t = t # Compute tentative velocity step begin("Computing tentative velocity") b1 = assemble(L1) [bc.apply(A1, b1) for bc in bcu] solve(A1, u1.vector(), b1, "gmres", "default") end() # Pressure correction begin("Computing pressure correction") b2 = assemble(L2) [bc.apply(A2, b2) for bc in bcp] solve(A2, p1.vector(), b2, "cg", prec) end() # Velocity correction begin("Computing velocity correction") b3 = assemble(L3) [bc.apply(A3, b3) for bc in bcu] solve(A3, u1.vector(), b3, "gmres", "default") end() # Plot solution plot(p1, title="Pressure", rescale=True) plot(u1, title="Velocity", rescale=True) # Save to file ufile << u1 pfile << p1 # Move to next time step un1.assign(u0) u0.assign(u1) t += dt print "t =", t # Hold plot interactive()

運行程序會顯示肘部周圍的流動。 自己運行科學計算代碼以查看動畫！ 最後一幀的屏幕如下所示。

模擬結束時彎曲處的相對壓力，按大小縮放和著色（無量綱值）：

模擬結束時彎曲處的相對速度作為矢量字形按大小（無量綱值）縮放和著色。

因此，我們所做的是採用現有的演示，它恰好很容易地實現了一個與我們非常相似的方案，並通過使用來自上一個時間步的信息對其進行了修改以使用更好的近似值。

在這一點上，您可能會認為這是一個微不足道的編輯。 確實如此，這在很大程度上是重點。 這個開源科學計算項目使我們能夠通過更改四行代碼快速實現修改後的數值模型。 在大型研究代碼中，此類更改可能需要數月時間。

該項目還有許多其他演示可以用作起點。 甚至在該項目上構建了許多開源應用程序，它們實現了各種模型。

結論

科學計算及其應用確實很複雜。 沒有辦法解決這個問題。 但正如在許多領域中越來越真實的那樣，可用開源工具和項目的不斷增長的格局可以顯著簡化原本極其複雜和乏味的編程任務。 或許，科學計算變得足夠容易，可以發現自己在研究界之外很容易被利用的時候已經很近了。

附錄：科學和數學基礎

對於那些感興趣的人，這裡是我們上面的計算流體動力學指南的技術基礎。 下面的內容將作為一個非常有用和簡明的主題摘要，這些主題通常涵蓋在十幾個研究生水平的課程中。 對深入理解該主題感興趣的研究生和數學類型可能會發現這些材料非常吸引人。

流體力學

一般來說，“建模”是用級數逼近求解某個實際系統的過程。 該模型通常會涉及不適合計算機實現的連續方程，因此必須用數值方法進一步近似。

對於流體力學，讓我們從基本方程 Navier-Stokes 方程開始本指南，並使用它來開發 CFD 方案。

Navier-Stokes 方程是一系列偏微分方程 (PDE)，它們很好地描述了流體流動，因此是我們的起點。 它們可以從通過雷諾傳輸定理並應用高斯定理並調用斯托克假設而得到的質量、動量和能量守恆定律推導出來。 這些方程需要一個連續假設，假設我們有足夠的流體粒子來給出統計特性，例如溫度、密度和速度含義。 此外，還需要表面應力張量和應變率張量之間的線性關係、應力張量的對稱性和各向同性流體假設。 了解我們在此開發過程中所做和繼承的假設非常重要，這樣我們才能評估結果代碼的適用性。 愛因斯坦表示法的 Navier-Stokes 方程，不用多說：

質量守恆：

動量守恆：

能量守恆：

其中偏應力為：

雖然非常普遍，可以控制物理世界中的大多數流體流動，但它們直接並沒有多大用處。 這些方程的已知精確解相對較少，而 1,000,000 美元的千禧年獎頒發給任何能夠解決存在性和平滑性問題的人。 重要的部分是我們通過一系列假設來降低複雜性（它們是經典物理學中一些最難的方程），從而為模型的開發提供了一個起點。

為了使事情保持“簡單”，我們將使用我們的領域特定知識對流體做出不可壓縮的假設，並假設恆定溫度，這樣就不需要（解耦）成為熱方程的能量守恆方程。 我們現在有兩個方程，仍然是 PDE，但在解決大量實際流體問題的同時要簡單得多。

連續性方程

動量方程

在這一點上，我們現在有一個很好的不可壓縮流體流動的數學模型（例如，低速氣體和液體，例如水）。 直接手動求解這些方程並不容易，但很高興我們可以獲得簡單問題的“精確”解。 使用這些方程來解決感興趣的問題，比如流過機翼的空氣或流過某個系統的水，需要我們對這些方程進行數值求解。

建立一個數值方案

為了使用計算機解決更複雜的問題，需要一種數值求解不可壓縮方程的方法。 在數值上求解偏微分方程甚至微分方程並非易事。 然而，我們在本指南中的方程式有一個特殊的挑戰（驚喜！）。 也就是說，我們需要求解動量方程，同時保持解散度不受連續性的要求。 通過像 Runge-Kutta 方法這樣的簡單時間積分變得困難，因為連續性方程中沒有時間導數。

沒有正確的，甚至是最好的求解方程的方法，但有許多可行的選擇。 幾十年來，已經發現了幾種解決該問題的方法，例如根據渦度和流函數重新制定公式，引入人工可壓縮性和算子分裂。 Chorin (1969)，然後是 Kim 和 Moin (1984, 1990)，制定了一種非常成功和流行的分步法，這將使我們能夠在直接而不是隱式求解壓力場的同時對方程進行積分。 分步法是一種通過分裂算子來逼近方程的一般方法，在這種情況下，沿著壓力分裂。 該方法相對簡單但穩健，促使其選擇此處。

首先，我們需要在時間上對方程進行數值區分，以便我們可以從一個時間點跨步到下一個時間點。 繼 Kim 和 Moin (1984) 之後，我們將對流項使用二階顯式 Adams-Bashforth 方法，粘性項使用二階隱式 Crank-Nicholson 方法，時間導數使用簡單的有限差分，同時忽略壓力梯度。 這些選擇絕不是唯一可以做出的近似：它們的選擇是通過控制方案的數值行為來構建方案的藝術的一部分。

中間速度現在可以積分，但是，它忽略了壓力的貢獻並且現在是發散的（不可壓縮性要求它是無發散的）。 需要運算符的其餘部分將我們帶到下一個時間步。

在哪裡是我們需要找到的一些標量，它會導致發散的自由速度。 我們可以找通過採取修正步驟的分歧，

其中第一項根據連續性的要求為零，產生標量場的泊松方程，該方程將在下一個時間步提供螺線管（無發散）速度。

正如 Kim 和 Moin (1984) 所示， 不完全是算子分裂造成的壓力，但可以通過

在本教程的這一點上，我們做得很好，我們已經對控制方程進行了時間離散化，以便我們可以整合它們。 我們現在需要對算子進行空間區分。 有許多方法可以實現這一點，例如，有限元法、有限體積法和有限差分法。 在 Kim 和 Moin (1984) 的原創作品中，他們採用了有限差分法。 該方法因其相對簡單和計算效率而具有優勢，但由於需要結構化網格，因此會受到復雜幾何形狀的影響。

有限元法 (FEM) 因其通用性而成為一種方便的選擇，並且有一些非常好的開源項目可以幫助其使用。 特別是它可以處理一維、二維和三維的真實幾何圖形，可以針對機器集群上的非常大的問題進行擴展，並且相對容易用於高階元素。 通常，該方法是這三種方法中較慢的一種，但它會給我們最大的解決問題的里程，所以我們將在這裡使用它。

即使在實施 FEM 時，也有很多選擇。 在這裡，我們將使用 Galerkin FEM。 在這樣做時，我們通過將每個方程乘以一個測試函數來將方程轉換為加權殘差形式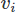對於向量和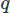對於標量場，並在域上積分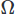. 然後我們使用斯托克定理或發散定理對任何高階導數進行部分積分。 然後我們提出變分問題，產生我們想要的 CFD 方案。

我們現在有一個很好的數學方案，以“方便”的形式實施，希望能對實現目標有一定的了解（大量數學，以及來自傑出研究人員的方法，我們幾乎複製和調整）。