Açık Kaynak Araçlarla Bilimsel Hesaplama Kılavuzu

Tarihsel olarak, hesaplamalı bilim, büyük ölçüde araştırma bilimcileri ve doktora adayları alanıyla sınırlandırılmıştır. Bununla birlikte, yıllar içinde -belki de daha geniş yazılım topluluğunun haberi olmadan- biz bilimsel bilgi işlem yumurta kafaları, ağır işlerin büyük çoğunluğunu kaldıran ortak çalışmaya dayalı açık kaynak kitaplıkları sessizce derliyoruz . Sonuç olarak, matematiksel modelleri uygulamak artık her zamankinden daha kolay ve alan henüz kitlesel tüketim için hazır olmasa da, başarılı uygulama çıtası büyük ölçüde düşürüldü. Sıfırdan yeni bir hesaplamalı kod tabanı geliştirmek, tipik olarak yıllar içinde ölçülen büyük bir girişimdir, ancak bu açık kaynaklı bilimsel hesaplama projeleri, bu hesaplama yeteneklerinden nispeten hızlı bir şekilde yararlanmak için erişilebilir örneklerle çalışmayı mümkün kılmaktadır.

Bilimsel hesaplamanın amacı, doğada var olan gerçek sistemlere bilimsel içgörü sağlamak olduğundan, disiplin, bilgisayar yazılımını gerçeğe dönüştürmede en ileri noktayı temsil eder. Gerçek dünyayı hem doğruluk hem de çözünürlük açısından çok yüksek düzeyde taklit eden bir yazılım yapmak için, üniversitelerin, ulusal laboratuvarların veya kurumsal Ar-Ge departmanlarının duvarlarının ötesinde nadiren bulunan bilgileri gerektiren karmaşık diferansiyel matematik çağrılmalıdır. Bunun da ötesinde, gerçek dünyanın sürekli, sonsuz küçük dokusunu sıfırların ve birlerin ayrı dilini kullanarak tanımlamaya çalışırken önemli sayısal zorluklar ortaya çıkar. Hem hesaplama açısından izlenebilir hem de anlamlı sonuçlar veren algoritmalar oluşturmak için dikkatli bir sayısal dönüşüm için kapsamlı bir çaba gereklidir. Başka bir deyişle, bilimsel hesaplama ağır bir iştir.

Bilimsel Hesaplama için Açık Kaynak Araçları

Şahsen ben özellikle FEniCS projesine bayılıyorum, onu tez çalışmam için kullanıyorum ve bu eğitim için kod örneğimiz için bunu seçme konusundaki önyargımı göstereceğim. (DUNE gibi kullanabileceğiniz çok kaliteli başka projeler de var.)

FEniCS kendini "sonlu eleman yöntemleriyle diferansiyel denklemlerin otomatik çözümüne özel olarak odaklanan, otomatik bilimsel hesaplama için yenilikçi konseptler ve araçların geliştirilmesi için ortak bir proje" olarak tanımlıyor. Bu, çok çeşitli sorunları ve bilimsel hesaplama uygulamalarını çözmek için güçlü bir kitaplıktır. Katkıda bulunanları arasında, son on yılda toplu olarak paha biçilmez bir kaynak haline getiren Simula Araştırma Laboratuvarı, Cambridge Üniversitesi, Chicago Üniversitesi, Baylor Üniversitesi ve KTH Kraliyet Teknoloji Enstitüsü bulunmaktadır (bkz. FEniCS codewarm).

Şaşırtıcı olan, FEniCS kütüphanesinin bizi ne kadar çabadan koruduğudur. Projenin kapsadığı konuların şaşırtıcı derinliğini ve genişliğini anlamak için, Bölüm 21'in sıkıştırılamaz akışları çözmek için çeşitli sonlu eleman şemalarını karşılaştırdığı açık kaynak kitaplarını görüntüleyebilirsiniz.

Perde arkasında, proje bizim için doğrudan ilgilenebilecek veya doğrudan kullanılabilecek çok sayıda açık kaynaklı bilimsel bilgi işlem kitaplığı entegre etti. Bunlar, belirli bir sıra olmaksızın, FEniCS projesinin öne çıkardığı projeleri içerir:

• PETSc: Kısmi diferansiyel denklemlerle modellenen bilimsel uygulamaların ölçeklenebilir (paralel) çözümü için bir veri yapıları ve rutinler paketi.
• Trilinos Projesi: Sandia Ulusal Laboratuarlarında yapılan çalışmalardan geliştirilen, hem doğrusal hem de doğrusal olmayan denklemleri çözmek için bir dizi sağlam algoritma ve teknoloji.
• uBLAS: "Yoğun, paketlenmiş ve seyrek matrisler için BLAS düzey 1, 2, 3 işlevselliği ve doğrusal cebir için birçok sayısal algoritma sağlayan bir C++ şablon sınıfı kitaplığı."
• GMP: İşaretli tamsayılar, rasyonel sayılar ve kayan noktalı sayılar üzerinde çalışan, isteğe bağlı hassas aritmetik için ücretsiz bir kitaplık.
• UMFPACK: Simetrik olmayan seyrek doğrusal sistemleri çözmek için bir dizi rutin, Ax=b, Simetrik Olmayan MultiFrontal yöntemini kullanarak.
• ParMETIS: Yapılandırılmamış grafikleri, ağları bölümlere ayırmak ve seyrek matrislerin dolgu azaltıcı sıralamalarını hesaplamak için çeşitli algoritmalar uygulayan MPI tabanlı bir paralel kitaplık.
• NumPy: Python ile bilimsel hesaplama için temel paket.
• CGAL: C++ kitaplığı biçiminde verimli ve güvenilir geometrik algoritmalar.
• SCOTCH: Sıralı ve paralel grafik bölümleme, statik haritalama ve kümeleme, sıralı ağ ve hipergraf bölümleme ve sıralı ve paralel seyrek matris blok sıralaması için bir yazılım paketi ve kitaplıkları.
• MPI: Akademi ve endüstriden bir grup araştırmacı tarafından çok çeşitli paralel bilgisayarlarda çalışmak üzere tasarlanmış standartlaştırılmış ve taşınabilir bir mesaj iletme sistemi.
• VTK: 3D bilgisayar grafikleri, görüntü işleme ve görselleştirme için açık kaynaklı, ücretsiz olarak kullanılabilen bir yazılım sistemi.
• SLEPc: Paralel bilgisayarlarda büyük ölçekli seyrek özdeğer problemlerinin çözümü için bir yazılım kütüphanesi.

Projeye entegre edilen bu harici paketler listesi, bize miras kalan yetenekleri hakkında bir fikir verir. Örneğin, MPI için entegre desteğe sahip olmak, bir bilgi işlem kümesi ortamında uzak çalışanlar arasında ölçeklendirmeye izin verir (yani, bu kod bir süper bilgisayarda veya dizüstü bilgisayarınızda çalışır).

Finansal modelleme, görüntü işleme, optimizasyon sorunları ve hatta belki video oyunları da dahil olmak üzere , bu projelerin kullanılabileceği bilimsel hesaplamanın ötesinde birçok uygulama olduğunu belirtmek de ilginçtir . Örneğin, bir oyuncunun etkileşime gireceği okyanus/nehir akıntıları gibi iki boyutlu bir sıvı akışını çözmek için bu açık kaynak algoritmaları ve tekniklerinden bazılarını kullanan bir video oyunu yaratmak mümkün olacaktır (belki deneyin ve deneyin). değişen rüzgar ve su akışlarına sahip bir tekneyle karşıya geçin).

Örnek Bir Uygulama: Bilimsel Hesaplama için Açık Kaynaktan Yararlanma

Burada, temel bir Hesaplamalı Akışkanlar Dinamiği şemasının bu açık kaynak kitaplıklarından birinde - bu durumda FEniCS projesinde - nasıl geliştirildiğini ve uygulandığını göstererek, sayısal bir model geliştirmenin ne içerdiğine dair bir fikir vermeye çalışacağım. FEnICS, hem Python hem de C++'da API'ler sağlar. Bu örnek için Python API'larını kullanacağız.

Biraz teknik içeriği tartışacağız, ancak amaç, bu tür bilimsel hesaplama kodunu geliştirmenin ne anlama geldiğine ve günümüzün açık kaynak araçlarının bizim için ne kadar ayak işi yaptığına dair bir fikir vermek olacaktır. Bu süreçte, umarım karmaşık bilimsel hesaplama dünyasının gizemini çözmeye yardımcı oluruz. (Bu ayrıntı düzeyiyle ilgilenenler için tüm matematiksel ve bilimsel temelleri ayrıntılandıran bir Ek verildiğine dikkat edin.)

SORUMLULUK REDDİ: Bilimsel bilgi işlem yazılımları ve uygulamaları konusunda çok az bilgisi olan veya hiç bilgisi olmayan okuyucular için, bu örneğin bazı bölümleri sizi şöyle hissettirebilir:

Eğer öyleyse, umutsuzluğa kapılmayın. Buradaki ana paket, mevcut açık kaynak projelerinin bu görevlerin çoğunu ne ölçüde basitleştirebileceğidir.

Bunu akılda tutarak, sıkıştırılamaz Navier-Stokes için FEnICS demosuna bakarak başlayalım. Bu demo, sıhhi tesisat borusu gibi L şeklinde bir kıvrımdan akan sıkıştırılamaz bir sıvının basıncını ve hızını modeller.

Bağlantılı demo sayfasındaki açıklama, kodu çalıştırmak için gerekli adımların mükemmel ve kısa bir kurulumunu sağlar ve neyin dahil olduğunu görmek için hızlıca bir göz atmanızı tavsiye ederim. Özetlemek gerekirse, demo sıkıştırılamaz akış denklemleri için viraj boyunca hız ve basıncı çözecektir. Demo, zaman içinde akan sıvının kısa bir simülasyonunu çalıştırır ve sonuçları ilerledikçe canlandırır. Bu, borudaki boşluğu temsil eden ağı kurarak ve ağ üzerindeki her noktadaki hız ve basıncı sayısal olarak çözmek için Sonlu Elemanlar Yöntemini kullanarak gerçekleştirilir. Daha sonra, elimizdeki denklemleri kullanarak hız ve basınç alanlarını güncelleyerek zaman içinde yineleniriz.

Demo olduğu gibi iyi çalışıyor, ancak onu biraz değiştireceğiz. Demo Chorin bölünmesini kullanıyor, ancak bunun yerine Kim ve Moin'den ilham alan biraz farklı yöntemi kullanacağız, bunun daha istikrarlı olduğunu umuyoruz. Bu sadece konvektif ve viskoz terimleri tahmin etmek için kullanılan denklemi değiştirmemizi gerektirir, ancak bunu yapmak için önceki zaman adımının hız alanını saklamamız ve güncelleme denklemine öncekini kullanacak olan iki ek terim eklememiz gerekir. Daha doğru bir sayısal yaklaşım için bilgi.

O halde bu değişikliği yapalım. İlk olarak setup'a yeni bir Function nesnesi ekliyoruz. Bu, vektör veya skaler alan gibi soyut bir matematiksel işlevi temsil eden bir nesnedir. Biz buna un1 , önceki hız alanını depolayacak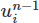 fonksiyon alanımızda V .

 ... # Create functions (three distinct vector fields and a scalar field) un1 = Function(V) # the previous time step's velocity field we are adding u0 = Function(V) # the current velocity field u1 = Function(V) # the next velocity field (what's being solved for) p1 = Function(Q) # the next pressure field (what's being solved for) ...

Ardından, simülasyonun her adımında “geçici hız”ın güncellenme şeklini değiştirmemiz gerekiyor. Bu alan, basıncın göz ardı edildiği bir sonraki zaman adımında yaklaşık hızı temsil eder (bu noktada basınç henüz bilinmemektedir). Chorin split yöntemini daha yeni Kim ve Moin fraksiyonel adım yöntemiyle değiştirdiğimiz yer burasıdır. Başka bir deyişle, F1 alanının ifadesini değiştireceğiz:

Yer değiştirmek:

 # Tentative velocity field (a first prediction of what the next velocity field is) # for the Chorin style split # F1 = change in the velocity field + # convective term + # diffusive term - # body force term F1 = (1/k)*inner(u - u0, v)*dx + \ inner(grad(u0)*u0, v)*dx + \ nu*inner(grad(u), grad(v))*dx - \ inner(f, v)*dx

İle birlikte:

 # Tentative velocity field (a first prediction of what the next velocity field is) # for the Kim and Moin style split # F1 = change in the velocity field + # convective term + # diffusive term - # body force term F1 = (1/k)*inner(u - u0, v)*dx + \ (3.0/2.0) * inner(grad(u0)*u0, v)*dx - (1.0/2.0) * inner(grad(un1)*un1, v)*dx + \ (nu/2.0)*inner(grad(u+u0), grad(v))*dx - \ inner(f, v)*dx

böylece demo artık F1 kullandığında ara hız alanını çözmek için güncellenmiş yöntemimizi kullanıyor.

Son olarak, her yineleme adımının sonunda önceki hız alanını, un1 güncellediğimizden emin olun.

 ... # Move to next time step un1.assign(u0) # copy the current velocity field into the previous velocity field u0.assign(u1) # copy the next velocity field into the current velocity field ...

FEniCS CFD demomuzun tam kodu, değişikliklerimiz dahil:

 """This demo program solves the incompressible Navier-Stokes equations on an L-shaped domain using Kim and Moin's fractional step method.""" # Begin demo from dolfin import * # Print log messages only from the root process in parallel parameters["std_out_all_processes"] = False; # Load mesh from file mesh = Mesh("lshape.xml.gz") # Define function spaces (P2-P1) V = VectorFunctionSpace(mesh, "Lagrange", 2) Q = FunctionSpace(mesh, "Lagrange", 1) # Define trial and test functions u = TrialFunction(V) p = TrialFunction(Q) v = TestFunction(V) q = TestFunction(Q) # Set parameter values dt = 0.01 T = 3 nu = 0.01 # Define time-dependent pressure boundary condition p_in = Expression("sin(3.0*t)", t=0.0) # Define boundary conditions noslip = DirichletBC(V, (0, 0), "on_boundary && \ (x[0] < DOLFIN_EPS | x[1] < DOLFIN_EPS | \ (x[0] > 0.5 - DOLFIN_EPS && x[1] > 0.5 - DOLFIN_EPS))") inflow = DirichletBC(Q, p_in, "x[1] > 1.0 - DOLFIN_EPS") outflow = DirichletBC(Q, 0, "x[0] > 1.0 - DOLFIN_EPS") bcu = [noslip] bcp = [inflow, outflow] # Create functions un1 = Function(V) u0 = Function(V) u1 = Function(V) p1 = Function(Q) # Define coefficients k = Constant(dt) f = Constant((0, 0)) # Tentative velocity field (a first prediction of what the next velocity field is) # for the Kim and Moin style split # F1 = change in the velocity field + # convective term + # diffusive term - # body force term F1 = (1/k)*inner(u - u0, v)*dx + \ (3.0/2.0) * inner(grad(u0)*u0, v)*dx - (1.0/2.0) * inner(grad(un1)*un1, v)*dx + \ (nu/2.0)*inner(grad(u+u0), grad(v))*dx - \ inner(f, v)*dx a1 = lhs(F1) L1 = rhs(F1) # Pressure update a2 = inner(grad(p), grad(q))*dx L2 = -(1/k)*div(u1)*q*dx # Velocity update a3 = inner(u, v)*dx L3 = inner(u1, v)*dx - k*inner(grad(p1), v)*dx # Assemble matrices A1 = assemble(a1) A2 = assemble(a2) A3 = assemble(a3) # Use amg preconditioner if available prec = "amg" if has_krylov_solver_preconditioner("amg") else "default" # Create files for storing solution ufile = File("results/velocity.pvd") pfile = File("results/pressure.pvd") # Time-stepping t = dt while t < T + DOLFIN_EPS: # Update pressure boundary condition p_in.t = t # Compute tentative velocity step begin("Computing tentative velocity") b1 = assemble(L1) [bc.apply(A1, b1) for bc in bcu] solve(A1, u1.vector(), b1, "gmres", "default") end() # Pressure correction begin("Computing pressure correction") b2 = assemble(L2) [bc.apply(A2, b2) for bc in bcp] solve(A2, p1.vector(), b2, "cg", prec) end() # Velocity correction begin("Computing velocity correction") b3 = assemble(L3) [bc.apply(A3, b3) for bc in bcu] solve(A3, u1.vector(), b3, "gmres", "default") end() # Plot solution plot(p1, title="Pressure", rescale=True) plot(u1, title="Velocity", rescale=True) # Save to file ufile << u1 pfile << p1 # Move to next time step un1.assign(u0) u0.assign(u1) t += dt print "t =", t # Hold plot interactive()

Programı çalıştırmak dirsek etrafındaki akışı gösterir. Animasyonunu görmek için bilimsel hesaplama kodunu kendiniz çalıştırın! Son çerçevenin ekranları aşağıda sunulmuştur.

Simülasyonun sonundaki bükümdeki göreli basınçlar, büyüklüğe göre ölçeklendirilmiş ve renklendirilmiştir (boyutsuz değerler):

Simülasyonun sonundaki bükümdeki nispi hızlar, büyüklük tarafından ölçeklendirilen ve renklendirilen vektör glifleri olarak (boyutsuz değerler).

Bu yüzden bizim yaptığımıza çok benzer bir şemayı kolayca uygulayan mevcut bir demoyu aldık ve önceki zaman adımından bilgileri kullanarak daha iyi yaklaşımlar kullanmak için değiştirdik.

Bu noktada bunun önemsiz bir düzenleme olduğunu düşünüyor olabilirsiniz. Öyleydi ve büyük ölçüde mesele bu. Bu açık kaynaklı bilimsel hesaplama projesi, dört satır kod değiştirerek değiştirilmiş bir sayısal modeli hızlı bir şekilde uygulamamıza izin verdi. Bu tür değişiklikler büyük araştırma kodlarında aylar alabilir.

Proje, başlangıç ​​noktası olarak kullanılabilecek başka birçok demoya sahiptir. Çeşitli modelleri uygulayan proje üzerine inşa edilmiş bir dizi açık kaynak uygulaması bile var.

Çözüm

Bilimsel hesaplama ve uygulamaları gerçekten karmaşıktır. Bunun etrafından dolaşmak yok. Ancak birçok alanda giderek artan bir şekilde geçerli olduğu gibi, mevcut açık kaynak araçlarının ve projelerinin sürekli büyüyen manzarası, aksi takdirde son derece karmaşık ve sıkıcı programlama görevlerini önemli ölçüde basitleştirebilir. Ve belki de, bilimsel hesaplamanın, araştırma topluluğunun ötesinde kolayca kullanıldığını bulabilecek kadar erişilebilir hale geldiği zaman yakındır.

EK: Bilimsel ve Matematiksel Temeller

İlgilenenler için, yukarıdaki Hesaplamalı Akışkanlar Dinamiği kılavuzumuzun teknik temellerini burada bulabilirsiniz. Aşağıdakiler, genellikle bir düzine kadar lisansüstü düzeydeki kurs boyunca kapsanan konuların çok yararlı ve özlü bir özeti olarak hizmet edecektir. Konunun derinlemesine anlaşılmasıyla ilgilenen lisansüstü öğrenciler ve matematik türleri bu materyali oldukça ilgi çekici bulabilir.

Akışkanlar mekaniği

Genel olarak “Modelleme”, bir dizi yaklaşımıyla bazı gerçek sistemleri çözme sürecidir. Model, genellikle bilgisayar uygulaması için uygun olmayan sürekli denklemleri içerecektir ve bu nedenle sayısal yöntemlerle daha fazla yaklaştırılmalıdır.

Akışkanlar mekaniği için, bu kılavuza temel denklemlerden, Navier-Stokes denklemlerinden başlayalım ve bunu bir CFD şeması geliştirmek için kullanalım.

Navier-Stokes denklemleri, sıvı akışlarını çok iyi tanımlayan ve bu nedenle başlangıç ​​noktamız olan bir dizi kısmi diferansiyel denklemdir (PDE'ler). Bunlar, bir Reynolds Transport Teoremi aracılığıyla atılan kütle, momentum ve enerji korunumu yasalarından ve Gauss teoreminin uygulanmasından ve Stoke's Hipotezinin başlatılmasından türetilebilir. Denklemler, sıcaklık, yoğunluk ve hız anlamı gibi istatistiksel özellikleri vermek için yeterli sıvı parçacığına sahip olduğumuzun varsayıldığı bir süreklilik varsayımı gerektirir. Ek olarak, yüzey gerilim tensörü ile gerinim hızı tensörü arasında doğrusal bir ilişki, gerilim tensöründe simetri ve izotropik akışkan varsayımlarına ihtiyaç vardır. Elde edilen koddaki uygulanabilirliği değerlendirebilmemiz için bu geliştirme sırasında yaptığımız ve devraldığımız varsayımları bilmek önemlidir. Lafı fazla uzatmadan Einstein notasyonundaki Navier-Stokes denklemleri:

Kütlenin korunumu:

Momentumun korunması:

Enerjinin korunumu:

deviatorik stresin olduğu yer:

Fiziksel dünyadaki çoğu akışkan akışını yöneten çok genel olmakla birlikte, doğrudan çok fazla kullanılmazlar. Denklemler için nispeten az bilinen kesin çözüm vardır ve varlık ve pürüzsüzlük problemini çözebilen herkes için 1.000.000 $'lık bir Milenyum Ödülü vardır. Önemli olan kısım, karmaşıklığı azaltmak için bir dizi varsayım yaparak modelimizin geliştirilmesi için bir başlangıç ​​noktasına sahip olmamızdır (bunlar klasik fizikteki en zor denklemlerden bazılarıdır).

İşleri “basit” tutmak için, akışkan üzerinde sıkıştırılamaz bir varsayımda bulunmak için alana özgü bilgimizi kullanacağız ve ısı denklemi haline gelen enerjinin korunumu denkleminin gerekli olmadığı (ayrışmış) şekilde sabit sıcaklıklar alacağız. Artık iki denklemimiz var, hala PDE'ler, ancak çok sayıda gerçek akışkan problemini çözerken önemli ölçüde daha basit.

Süreklilik denklemi

momentum denklemleri

Bu noktada artık sıkıştırılamaz akışkan akışları için güzel bir matematiksel modelimiz var (örneğin düşük hızlı gazlar ve su gibi sıvılar). Bu denklemleri doğrudan elle çözmek kolay değil, ancak basit problemler için “kesin” çözümler elde edebilmemiz güzel. Bir kanat üzerinden akan hava veya bir sistemden akan su gibi ilgili sorunları ele almak için bu denklemleri kullanmak, bu denklemleri sayısal olarak çözmemizi gerektirir.

Sayısal Bir Şema Oluşturma

Bilgisayarı kullanarak daha karmaşık problemleri çözmek için, sıkıştırılamaz denklemlerimizi sayısal olarak çözecek bir yönteme ihtiyaç vardır. Kısmi diferansiyel denklemleri, hatta diferansiyel denklemleri sayısal olarak çözmek önemsiz değildir. Ancak, bu kılavuzdaki denklemlerimizin özel bir zorluğu var (sürpriz!). Yani, sürekliliğin gerektirdiği gibi, çözüm sapmasını serbest tutarken momentum denklemlerini çözmemiz gerekiyor. Runge-Kutta yöntemi gibi basit bir zaman entegrasyonu, süreklilik denkleminin içinde bir zaman türevi olmadığı için zorlaştırılır.

Denklemleri çözmek için doğru, hatta en iyi yöntem yoktur, ancak uygulanabilir birçok seçenek vardır. Onlarca yıl boyunca, girdap ve akış fonksiyonu açısından yeniden formüle etme, yapay sıkıştırılabilirliği tanıtma ve operatör ayırma gibi konuyu ele alan çeşitli yaklaşımlar bulunmuştur. Chorin (1969) ve ardından Kim ve Moin (1984, 1990), basınç alanını dolaylı olarak değil doğrudan çözerken denklemleri entegre etmemize izin verecek çok başarılı ve popüler bir kesirli adım yöntemi formüle ettiler. Kesirli adım yöntemi, operatörlerini bölerek, bu durumda basınç boyunca bölme yaparak denklemlere yaklaşmak için genel bir yöntemdir. Yaklaşım nispeten basit ve yine de sağlam, burada seçimini motive ediyor.

İlk olarak, zaman içinde bir noktadan diğerine geçebilmemiz için denklemleri zaman içinde sayısal olarak ayırmamız gerekir. Kim ve Moin'i (1984) takip ederek, konvektif terimler için ikinci dereceden açık Adams-Bashforth yöntemini, viskoz terimler için ikinci dereceden örtük Crank-Nicholson yöntemini, zaman türevi için basit bir sonlu fark kullanacağız. , basınç gradyanını ihmal ederken. Bu seçimler, yapılabilecek tek yaklaşım değildir: bunların seçimi, şemanın sayısal davranışını kontrol ederek şemayı oluşturma sanatının bir parçasıdır.

Ara hız şimdi entegre edilebilir, ancak basıncın katkısını göz ardı eder ve şimdi ıraksaktır (sıkıştırılamazlık onun ıraksaksız olmasını gerektirir). Operatörün geri kalanı, bizi bir sonraki zaman adımına getirmek için gereklidir.

nerede ıraksak bir serbest hız ile sonuçlanan bulmamız gereken bir skalerdir. Bulabiliriz düzeltme adımının diverjansı alınarak,

ilk terimin sürekliliğin gerektirdiği şekilde sıfır olduğu yerde, bir sonraki zaman adımında solenoidal (ıraksaksız) bir hız sağlayacak bir skaler alan için bir Poisson denklemi elde edilir.

Kim ve Moin'in (1984) gösterdiği gibi, operatörün bölünmesinin bir sonucu olarak tam olarak basınç değildir, ancak şu şekilde bulunabilir:

Eğitimin bu noktasında oldukça iyi gidiyoruz, onları entegre edebilmek için yöneten denklemleri geçici olarak ayırdık. Şimdi operatörleri uzamsal olarak ayırmamız gerekiyor. Bunu başarabileceğimiz bir dizi yöntem mevcuttur, örneğin Sonlu Elemanlar Yöntemi, Sonlu Hacim Yöntemi ve Sonlu Farklar Yöntemi. Kim ve Moin'in (1984) orijinal çalışmasında Sonlu Farklar Yöntemi ile ilerlerler. Yöntem, göreceli basitliği ve hesaplama verimliliği açısından avantajlıdır, ancak yapılandırılmış bir ağ gerektirdiğinden karmaşık geometriler için sıkıntı çeker.

Sonlu Elemanlar Yöntemi (FEM), genelliği için uygun bir seçimdir ve kullanımına yardımcı olan çok güzel açık kaynaklı projelere sahiptir. Özellikle gerçek geometrileri bir, iki ve üç boyutta ele alır, makine kümelerinde çok büyük problemler için ölçekler ve yüksek dereceli elemanlar için kullanımı nispeten kolaydır. Tipik olarak yöntem üç yöntemden daha yavaştır, ancak bize problemler arasında en fazla mesafeyi verecektir, bu yüzden burada kullanacağız.

FEM'i uygularken bile birçok seçenek vardır. Burada Galerkin FEM'i kullanacağız. Bunu yaparken, denklemleri her birini bir test fonksiyonu ile çarparak ağırlıklı artık formda oluşturuyoruz.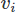 vektörler için ve 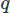skaler alan için ve etki alanı üzerinde entegrasyon 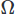. Daha sonra Stoke teoremini veya Diverjans teoremini kullanarak herhangi bir yüksek dereceli türev üzerinde kısmi entegrasyon gerçekleştiririz. Ardından, istenen CFD şemasını veren varyasyon problemini ortaya koyarız.

Şimdi, uygulama için "uygun" bir formda güzel bir matematiksel şemaya sahibiz, umarım oraya ulaşmak için ne gerektiğine dair bir fikirle (çok sayıda matematik ve hemen hemen kopyalayıp ince ayar yaptığımız parlak araştırmacılardan gelen yöntemler).