คู่มือคอมพิวเตอร์ทางวิทยาศาสตร์ด้วยเครื่องมือโอเพ่นซอร์ส

ในอดีต วิทยาการคำนวณส่วนใหญ่จำกัดอยู่ในขอบเขตของนักวิทยาศาสตร์การวิจัยและผู้สมัครระดับปริญญาเอก อย่างไรก็ตาม ในช่วงหลายปีที่ผ่านมา ซึ่งชุมชนซอฟต์แวร์ขนาดใหญ่กว่านั้นอาจไม่เคยรู้จักมาก่อน เราต่างพยายามรวบรวมไลบรารีโอเพนซอร์ซที่ทำงานร่วมกันอย่างเงียบๆ ซึ่งรองรับการยกของหนักส่วนใหญ่ ผลที่ได้คือตอนนี้การนำแบบจำลองทางคณิตศาสตร์ไปใช้นั้นง่ายกว่าที่เคย และในขณะที่ภาคสนามอาจยังไม่พร้อมสำหรับการบริโภคในปริมาณมาก แถบในการนำไปใช้ที่ประสบความสำเร็จก็ลดลงอย่างมาก การพัฒนาฐานโค้ดการคำนวณใหม่ตั้งแต่ต้นเป็นงานใหญ่ ซึ่งโดยทั่วไปแล้วจะวัดได้ในช่วงหลายปี แต่โปรเจ็กต์คอมพิวเตอร์ทางวิทยาศาสตร์แบบโอเพนซอร์สเหล่านี้ทำให้สามารถเรียกใช้ด้วยตัวอย่างที่เข้าถึงได้ เพื่อยกระดับความสามารถในการคำนวณเหล่านี้อย่างรวดเร็ว

เนื่องจากจุดประสงค์ของการคำนวณทางวิทยาศาสตร์คือการให้ข้อมูลเชิงลึกทางวิทยาศาสตร์เกี่ยวกับระบบที่มีอยู่จริงในธรรมชาติ วินัยจึงเป็นตัวแทนของความล้ำหน้าในการทำให้ซอฟต์แวร์คอมพิวเตอร์เข้าใกล้ความเป็นจริง ในการสร้างซอฟต์แวร์ที่เลียนแบบโลกแห่งความจริงทั้งในด้านความแม่นยำและความละเอียดในระดับสูง จะต้องเรียกใช้คณิตศาสตร์เชิงอนุพันธ์ที่ซับซ้อน ซึ่งต้องใช้ความรู้ที่หาได้ยากนอกกำแพงของมหาวิทยาลัย ห้องปฏิบัติการแห่งชาติ หรือแผนก R&D ขององค์กร ยิ่งไปกว่านั้น ความท้าทายด้านตัวเลขที่มีนัยสำคัญปรากฏขึ้นเมื่อพยายามอธิบายโครงสร้างที่ต่อเนื่องและมีขนาดเล็กของโลกแห่งความเป็นจริงโดยใช้ภาษาที่แยกจากกันของศูนย์และคน ต้องใช้ความพยายามอย่างละเอียดถี่ถ้วนในการแปลงตัวเลขอย่างระมัดระวังเพื่อแสดงอัลกอริธึมที่สามารถคำนวณได้และให้ผลลัพธ์ที่มีความหมาย กล่าวอีกนัยหนึ่ง คอมพิวเตอร์เชิงวิทยาศาสตร์เป็นงานหนัก

เครื่องมือโอเพ่นซอร์สสำหรับคอมพิวเตอร์ทางวิทยาศาสตร์

โดยส่วนตัวแล้วฉันชอบโครงการ FEniCS โดยเฉพาะอย่างยิ่ง ใช้สำหรับวิทยานิพนธ์ของฉัน และจะแสดงอคติของฉันในการเลือกสิ่งนั้นสำหรับตัวอย่างโค้ดของเราสำหรับบทช่วยสอนนี้ (มีโครงการคุณภาพสูงอื่น ๆ เช่น DUNE ซึ่งก็สามารถใช้ได้เช่นกัน)

FEniCS อธิบายตนเองว่าเป็น "โครงการความร่วมมือเพื่อพัฒนาแนวคิดและเครื่องมือที่เป็นนวัตกรรมใหม่สำหรับการคำนวณทางวิทยาศาสตร์แบบอัตโนมัติ โดยมุ่งเน้นเฉพาะที่การแก้ปัญหาอัตโนมัติของสมการเชิงอนุพันธ์โดยวิธีไฟไนต์เอลิเมนต์" นี่คือไลบรารีอันทรงพลังสำหรับการแก้ปัญหามากมายและแอปพลิเคชันการคำนวณทางวิทยาศาสตร์ ผู้ร่วมให้ข้อมูล ได้แก่ Simula Research Laboratory, University of Cambridge, University of Chicago, Baylor University และ KTH Royal Institute of Technology ที่ร่วมกันสร้างให้เป็นทรัพยากรอันล้ำค่าตลอดช่วงทศวรรษที่ผ่านมา (ดู FEniCS codeswarm)

สิ่งที่น่าประหลาดใจมากก็คือความพยายามที่ห้องสมุด FEniCS ปกป้องเราไว้ เพื่อให้เข้าใจถึงความลึกและความกว้างของหัวข้อที่น่าทึ่ง โปรเจ็กต์ครอบคลุมสามารถดูหนังสือเรียนแบบโอเพ่นซอร์สได้ โดยที่บทที่ 21 จะเปรียบเทียบโครงร่างไฟไนต์เอลิเมนต์ต่างๆ สำหรับการแก้ปัญหาโฟลว์ที่ไม่สามารถบีบอัดได้

เบื้องหลังโครงการได้รวมไลบรารีคอมพิวเตอร์ทางวิทยาศาสตร์แบบโอเพ่นซอร์สชุดใหญ่ไว้ให้เรา ซึ่งอาจเป็นประโยชน์หรือนำไปใช้โดยตรง ซึ่งรวมถึงโครงการต่างๆ ที่โครงการ FEniCS เรียกร้องโดยไม่เรียงลำดับเฉพาะ:

• PETSc: ชุดโครงสร้างข้อมูลและรูทีนสำหรับโซลูชันที่ปรับขนาดได้ (ขนาน) ของแอปพลิเคชันทางวิทยาศาสตร์ซึ่งจำลองโดยสมการเชิงอนุพันธ์ย่อย
• โครงการ Trilinos: ชุดของอัลกอริธึมและเทคโนโลยีที่มีประสิทธิภาพสำหรับการแก้สมการเชิงเส้นและไม่ใช่เชิงเส้น พัฒนาจากงานที่ Sandia National Labs
• uBLAS: "ไลบรารีคลาสเทมเพลต C++ ที่มีฟังก์ชัน BLAS ระดับ 1, 2, 3 สำหรับเมทริกซ์หนาแน่น อัดแน่น และกระจัดกระจาย และอัลกอริทึมตัวเลขจำนวนมากสำหรับพีชคณิตเชิงเส้น"
• GMP: ห้องสมุดฟรีสำหรับการคำนวณทางคณิตศาสตร์ที่แม่นยำโดยอำเภอใจ ดำเนินการกับจำนวนเต็มที่มีเครื่องหมาย ตัวเลขที่เป็นตรรกยะ และตัวเลขทศนิยม
• UMFPACK: ชุดของรูทีนสำหรับการแก้ระบบเชิงเส้นเบาบางที่ไม่สมมาตร Ax=b โดยใช้วิธี Unsymmetric MultiFrontal
• ParMETIS: ไลบรารีคู่ขนานแบบ MPI ที่ใช้อัลกอริธึมที่หลากหลายสำหรับการแบ่งพาร์ติชั่นกราฟแบบไม่มีโครงสร้าง เมช และสำหรับการคำนวณการเรียงลำดับเมทริกซ์เบาบาง
• NumPy: แพ็คเกจพื้นฐานสำหรับการคำนวณทางวิทยาศาสตร์ด้วย Python
• CGAL: อัลกอริธึมทางเรขาคณิตที่มีประสิทธิภาพและเชื่อถือได้ในรูปแบบของไลบรารี C++
• SCOTCH: แพ็คเกจซอฟต์แวร์และไลบรารีสำหรับการแบ่งพาร์ติชั่นกราฟแบบต่อเนื่องและแบบขนาน การทำแผนที่และการจัดกลุ่มสแตติก การแบ่งตาข่ายและการแบ่งไฮเปอร์กราฟตามลำดับ และการจัดลำดับบล็อกเมทริกซ์กระจัดกระจายแบบต่อเนื่องและแบบคู่ขนาน
• MPI: ระบบส่งข้อความที่ได้มาตรฐานและพกพาได้ ออกแบบโดยกลุ่มนักวิจัยจากภาควิชาการและอุตสาหกรรม เพื่อใช้งานบนคอมพิวเตอร์แบบคู่ขนานที่หลากหลาย
• VTK: ระบบซอฟต์แวร์โอเพนซอร์สที่ให้บริการฟรีสำหรับคอมพิวเตอร์กราฟิก 3 มิติ การประมวลผลภาพ และการแสดงภาพ
• SLEPc: ไลบรารีซอฟต์แวร์สำหรับการแก้ปัญหาค่าลักษณะเฉพาะแบบกระจัดกระจายขนาดใหญ่บนคอมพิวเตอร์แบบขนาน

รายการแพ็คเกจภายนอกที่รวมเข้ากับโปรเจ็กต์นี้ทำให้เราเข้าใจถึงความสามารถที่สืบทอดมา ตัวอย่างเช่น การรองรับ MPI แบบบูรณาการทำให้สามารถปรับขนาดข้ามผู้ปฏิบัติงานระยะไกลในสภาพแวดล้อมคลัสเตอร์การประมวลผล (เช่น รหัสนี้จะทำงานบนซูเปอร์คอมพิวเตอร์หรือแล็ปท็อปของคุณ)

นอกจากนี้ยังเป็นที่น่าสนใจที่จะทราบว่ามีแอปพลิเคชั่นมากมายนอกเหนือจากการคำนวณทางวิทยาศาสตร์ซึ่งโครงการเหล่านี้สามารถนำมาใช้ได้ รวมถึงการสร้างแบบจำลองทางการเงิน การประมวลผลภาพ ปัญหาการปรับให้เหมาะสม และบางทีแม้แต่วิดีโอเกม อาจเป็นไปได้ ตัวอย่างเช่น ในการสร้างวิดีโอเกมที่ใช้อัลกอริธึมและเทคนิคโอเพ่นซอร์สบางส่วนเหล่านี้เพื่อแก้ปัญหาการไหลของของไหลสองมิติ เช่น กระแสน้ำในมหาสมุทร/แม่น้ำที่ผู้เล่นโต้ตอบด้วย (อาจลองและ แล่นเรือไปตามลมและกระแสน้ำที่แตกต่างกัน)

แอปพลิเคชันตัวอย่าง: ใช้ประโยชน์จากโอเพ่นซอร์สสำหรับคอมพิวเตอร์ทางวิทยาศาสตร์

ในที่นี้ ฉันจะพยายามอธิบายให้เข้าใจถึงสิ่งที่การพัฒนาแบบจำลองเชิงตัวเลขเกี่ยวข้องกับการแสดงให้เห็นว่าโครงการ Computational Fluid Dynamics ขั้นพื้นฐานได้รับการพัฒนาและนำไปใช้ในหนึ่งในไลบรารีโอเพนซอร์สเหล่านี้อย่างไร ในกรณีนี้คือโครงการ FEniCS FEnICS มี API ทั้งใน Python และ C++ สำหรับตัวอย่างนี้ เราจะใช้ Python API

เราจะหารือเกี่ยวกับเนื้อหาที่ค่อนข้างเป็นทางเทคนิค แต่เป้าหมายก็คือเพื่อให้เห็นถึงสิ่งที่การพัฒนารหัสการคำนวณทางวิทยาศาสตร์นั้นเกี่ยวข้อง และเครื่องมือโอเพนซอร์สที่ใช้ได้ผลจริงในปัจจุบันทำเพื่อเรามากเพียงใด ในกระบวนการนี้ หวังว่าเราจะช่วยให้กระจ่างชัดในโลกที่ซับซ้อนของการคำนวณทางวิทยาศาสตร์ (โปรดทราบว่าภาคผนวกมีให้รายละเอียดพื้นฐานทางคณิตศาสตร์และวิทยาศาสตร์ทั้งหมดสำหรับผู้ที่สนใจในรายละเอียดระดับนั้น)

การปฏิเสธความ รับผิด: สำหรับผู้อ่านที่มีพื้นฐานเพียงเล็กน้อยหรือไม่มีเลยในซอฟต์แวร์และแอปพลิเคชันการคำนวณทางวิทยาศาสตร์ บางส่วนของตัวอย่างนี้อาจทำให้คุณรู้สึกเช่นนี้:

ถ้าเป็นเช่นนั้นอย่าสิ้นหวัง ประเด็นหลักที่นี่คือขอบเขตที่โครงการโอเพนซอร์สที่มีอยู่สามารถลดความซับซ้อนของงานเหล่านี้ได้อย่างมาก

ด้วยเหตุนี้ เรามาเริ่มด้วยการดูการสาธิต FEnICS สำหรับ Navier-Stokes ที่บีบอัดไม่ได้ การสาธิตนี้จำลองแรงดันและความเร็วของของไหลที่ไม่สามารถบีบอัดได้ซึ่งไหลผ่านส่วนโค้งรูปตัว L เช่น ท่อประปา

คำอธิบายในหน้าสาธิตที่ลิงก์ไว้ช่วยให้ตั้งค่าขั้นตอนที่จำเป็นสำหรับการรันโค้ดได้อย่างดีเยี่ยมและกระชับ เราขอแนะนำให้คุณดูอย่างรวดเร็วว่ามีอะไรเกี่ยวข้องบ้าง โดยสรุป การสาธิตจะแก้ความเร็วและความดันผ่านส่วนโค้งสำหรับสมการการไหลแบบบีบอัดไม่ได้ การสาธิตใช้การจำลองสั้นๆ ของของไหลที่ไหลไปตามกาลเวลา โดยสร้างภาพเคลื่อนไหวตามผลลัพธ์ ซึ่งทำได้โดยการตั้งค่าตาข่ายแทนพื้นที่ในท่อ และใช้วิธีไฟไนต์เอลิเมนต์เพื่อแก้ความเร็วและแรงดันที่แต่ละจุดบนตาข่ายเป็นตัวเลข จากนั้นเราวนซ้ำตลอดเวลา อัปเดตสนามความเร็วและแรงดันในขณะที่เราไป อีกครั้งโดยใช้สมการที่เรามีอยู่

การสาธิตทำงานได้ดีตามที่เป็นอยู่ แต่เราจะปรับเปลี่ยนเล็กน้อย การสาธิตใช้การแยก Chorin แต่เราจะใช้วิธีการที่แตกต่างกันเล็กน้อยซึ่งได้รับแรงบันดาลใจจาก Kim และ Moin แทน ซึ่งเราหวังว่าจะมีเสถียรภาพมากขึ้น นี่แค่ต้องการให้เราเปลี่ยนสมการที่ใช้ในการประมาณค่าการพาความร้อนและความหนืด แต่การทำเช่นนั้น เราจำเป็นต้องเก็บสนามความเร็วของขั้นตอนเวลาก่อนหน้า และเพิ่มคำศัพท์เพิ่มเติมสองคำในสมการการอัพเดท ซึ่งจะใช้อันก่อนหน้านั้น ข้อมูลเพื่อการประมาณตัวเลขที่แม่นยำยิ่งขึ้น

มาทำการเปลี่ยนแปลงนี้กัน ขั้นแรก เราเพิ่มอ็อบเจกต์ Function ใหม่ให้กับการตั้งค่า นี่คือวัตถุที่แสดงฟังก์ชันทางคณิตศาสตร์ที่เป็นนามธรรม เช่น เวกเตอร์หรือสนามสเกลาร์ เราจะเรียกมันว่า un1 มันจะเก็บสนามความเร็วก่อนหน้า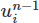 บนพื้นที่ทำงานของเรา V .

 ... # Create functions (three distinct vector fields and a scalar field) un1 = Function(V) # the previous time step's velocity field we are adding u0 = Function(V) # the current velocity field u1 = Function(V) # the next velocity field (what's being solved for) p1 = Function(Q) # the next pressure field (what's being solved for) ...

ต่อไป เราต้องเปลี่ยนวิธีอัปเดต "ความเร็วเบื้องต้น" ในระหว่างแต่ละขั้นตอนของการจำลอง สนามนี้แสดงความเร็วโดยประมาณในขั้นถัดไปเมื่อละเลยความดัน (ยังไม่ทราบความกดดัน ณ จุดนี้) นี่คือที่ที่เราแทนที่วิธีการแยก Chorin ด้วยวิธีขั้นตอนเศษส่วนของ Kim และ Moin ล่าสุด กล่าวอีกนัยหนึ่ง เราจะเปลี่ยนนิพจน์สำหรับฟิลด์ F1 :

แทนที่:

 # Tentative velocity field (a first prediction of what the next velocity field is) # for the Chorin style split # F1 = change in the velocity field + # convective term + # diffusive term - # body force term F1 = (1/k)*inner(u - u0, v)*dx + \ inner(grad(u0)*u0, v)*dx + \ nu*inner(grad(u), grad(v))*dx - \ inner(f, v)*dx

กับ:

 # Tentative velocity field (a first prediction of what the next velocity field is) # for the Kim and Moin style split # F1 = change in the velocity field + # convective term + # diffusive term - # body force term F1 = (1/k)*inner(u - u0, v)*dx + \ (3.0/2.0) * inner(grad(u0)*u0, v)*dx - (1.0/2.0) * inner(grad(un1)*un1, v)*dx + \ (nu/2.0)*inner(grad(u+u0), grad(v))*dx - \ inner(f, v)*dx

เพื่อให้การสาธิตใช้วิธีการที่อัปเดตของเราในการแก้ปัญหาสำหรับสนามความเร็วกลางเมื่อใช้ F1

สุดท้าย ตรวจสอบให้แน่ใจว่าเรากำลังอัปเดตฟิลด์ความเร็วก่อนหน้า un1 ในตอนท้ายของแต่ละขั้นตอนการวนซ้ำ

 ... # Move to next time step un1.assign(u0) # copy the current velocity field into the previous velocity field u0.assign(u1) # copy the next velocity field into the current velocity field ...

เพื่อให้ต่อไปนี้เป็นโค้ดที่สมบูรณ์จากการสาธิต FEniCS CFD ของเรา โดยรวมถึงการเปลี่ยนแปลงของเราด้วย:

 """This demo program solves the incompressible Navier-Stokes equations on an L-shaped domain using Kim and Moin's fractional step method.""" # Begin demo from dolfin import * # Print log messages only from the root process in parallel parameters["std_out_all_processes"] = False; # Load mesh from file mesh = Mesh("lshape.xml.gz") # Define function spaces (P2-P1) V = VectorFunctionSpace(mesh, "Lagrange", 2) Q = FunctionSpace(mesh, "Lagrange", 1) # Define trial and test functions u = TrialFunction(V) p = TrialFunction(Q) v = TestFunction(V) q = TestFunction(Q) # Set parameter values dt = 0.01 T = 3 nu = 0.01 # Define time-dependent pressure boundary condition p_in = Expression("sin(3.0*t)", t=0.0) # Define boundary conditions noslip = DirichletBC(V, (0, 0), "on_boundary && \ (x[0] < DOLFIN_EPS | x[1] < DOLFIN_EPS | \ (x[0] > 0.5 - DOLFIN_EPS && x[1] > 0.5 - DOLFIN_EPS))") inflow = DirichletBC(Q, p_in, "x[1] > 1.0 - DOLFIN_EPS") outflow = DirichletBC(Q, 0, "x[0] > 1.0 - DOLFIN_EPS") bcu = [noslip] bcp = [inflow, outflow] # Create functions un1 = Function(V) u0 = Function(V) u1 = Function(V) p1 = Function(Q) # Define coefficients k = Constant(dt) f = Constant((0, 0)) # Tentative velocity field (a first prediction of what the next velocity field is) # for the Kim and Moin style split # F1 = change in the velocity field + # convective term + # diffusive term - # body force term F1 = (1/k)*inner(u - u0, v)*dx + \ (3.0/2.0) * inner(grad(u0)*u0, v)*dx - (1.0/2.0) * inner(grad(un1)*un1, v)*dx + \ (nu/2.0)*inner(grad(u+u0), grad(v))*dx - \ inner(f, v)*dx a1 = lhs(F1) L1 = rhs(F1) # Pressure update a2 = inner(grad(p), grad(q))*dx L2 = -(1/k)*div(u1)*q*dx # Velocity update a3 = inner(u, v)*dx L3 = inner(u1, v)*dx - k*inner(grad(p1), v)*dx # Assemble matrices A1 = assemble(a1) A2 = assemble(a2) A3 = assemble(a3) # Use amg preconditioner if available prec = "amg" if has_krylov_solver_preconditioner("amg") else "default" # Create files for storing solution ufile = File("results/velocity.pvd") pfile = File("results/pressure.pvd") # Time-stepping t = dt while t < T + DOLFIN_EPS: # Update pressure boundary condition p_in.t = t # Compute tentative velocity step begin("Computing tentative velocity") b1 = assemble(L1) [bc.apply(A1, b1) for bc in bcu] solve(A1, u1.vector(), b1, "gmres", "default") end() # Pressure correction begin("Computing pressure correction") b2 = assemble(L2) [bc.apply(A2, b2) for bc in bcp] solve(A2, p1.vector(), b2, "cg", prec) end() # Velocity correction begin("Computing velocity correction") b3 = assemble(L3) [bc.apply(A3, b3) for bc in bcu] solve(A3, u1.vector(), b3, "gmres", "default") end() # Plot solution plot(p1, title="Pressure", rescale=True) plot(u1, title="Velocity", rescale=True) # Save to file ufile << u1 pfile << p1 # Move to next time step un1.assign(u0) u0.assign(u1) t += dt print "t =", t # Hold plot interactive()

การรันโปรแกรมแสดงการไหลรอบข้อศอก รันโค้ดการคำนวณทางวิทยาศาสตร์ด้วยตัวเองเพื่อให้มันเคลื่อนไหว! หน้าจอของเฟรมสุดท้ายแสดงอยู่ด้านล่าง

ความดันสัมพัทธ์ในส่วนโค้งเมื่อสิ้นสุดการจำลอง ปรับขนาดและระบายสีตามขนาด (ค่าที่ไม่ใช่มิติ):

ความเร็วสัมพัทธ์ในส่วนโค้งที่ส่วนท้ายของการจำลองเป็นภาพเวกเตอร์ที่ปรับขนาดและระบายสีตามขนาด (ค่าที่ไม่ใช่มิติ)

ดังนั้นสิ่งที่เราทำคือนำการสาธิตที่มีอยู่มาใช้ ซึ่งเกิดขึ้นเพื่อใช้รูปแบบที่คล้ายกับของเราค่อนข้างง่าย และแก้ไขให้ใช้การประมาณที่ดีขึ้นโดยใช้ข้อมูลจากขั้นตอนเวลาก่อนหน้า

ณ จุดนี้คุณอาจคิดว่าเป็นการแก้ไขเล็กน้อย มันเป็นและนั่นคือประเด็นส่วนใหญ่ โครงการคอมพิวเตอร์ทางวิทยาศาสตร์แบบโอเพนซอร์สนี้ช่วยให้เรานำแบบจำลองตัวเลขที่แก้ไขแล้วไปใช้ได้อย่างรวดเร็วโดยการเปลี่ยนโค้ดสี่บรรทัด การเปลี่ยนแปลงดังกล่าวอาจใช้เวลาหลายเดือนในรหัสการวิจัยขนาดใหญ่

โครงการมีการสาธิตอื่น ๆ อีกมากมายซึ่งสามารถใช้เป็นจุดเริ่มต้นได้ มีแอปพลิเคชันโอเพ่นซอร์สจำนวนมากที่สร้างขึ้นในโครงการซึ่งใช้โมเดลต่างๆ

บทสรุป

การคำนวณทางวิทยาศาสตร์และการประยุกต์นั้นซับซ้อนอย่างแท้จริง ไม่มีการไปไหนมาไหน แต่ตามที่เป็นจริงมากขึ้นในหลายโดเมน ภูมิทัศน์ที่เพิ่มมากขึ้นเรื่อยๆ ของเครื่องมือและโครงการโอเพ่นซอร์สที่มีอยู่ สามารถลดความซับซ้อนของงานเขียนโปรแกรมที่ซับซ้อนและน่าเบื่อได้อย่างมาก และบางทีอาจถึงเวลาแล้วที่คอมพิวเตอร์วิทยาศาสตร์จะสามารถเข้าถึงได้มากพอที่จะพบว่าตัวเองถูกนำไปใช้อย่างง่ายดายนอกเหนือจากชุมชนการวิจัย

ภาคผนวก: รากฐานทางวิทยาศาสตร์และคณิตศาสตร์

สำหรับผู้ที่สนใจ นี่คือการสนับสนุนทางเทคนิคของคู่มือ Computational Fluid Dynamics ด้านบน สิ่งต่อไปนี้จะทำหน้าที่เป็นบทสรุปที่เป็นประโยชน์และรัดกุมของหัวข้อที่โดยทั่วไปจะครอบคลุมตลอดหลักสูตรระดับบัณฑิตศึกษาหลายสิบหลักสูตร นักศึกษาระดับบัณฑิตศึกษาและประเภทคณิตศาสตร์ที่สนใจในความเข้าใจอย่างลึกซึ้งในหัวข้อนี้อาจพบว่าเนื้อหานี้ค่อนข้างมีส่วนร่วม

กลศาสตร์ของไหล

โดยทั่วไป “การสร้างแบบจำลอง” เป็นกระบวนการในการแก้ไขระบบจริงบางระบบด้วยการประมาณแบบอนุกรม แบบจำลองนี้มักจะเกี่ยวข้องกับสมการต่อเนื่องที่ไม่เหมาะกับการนำคอมพิวเตอร์ไปใช้ ดังนั้นจึงต้องมีการประมาณค่าด้วยวิธีตัวเลขเพิ่มเติม

สำหรับกลศาสตร์ของไหล เรามาเริ่มคู่มือนี้จากสมการพื้นฐาน สมการเนเวียร์-สโตกส์ และใช้สิ่งนั้นเพื่อพัฒนารูปแบบ CFD

สมการเนเวียร์-สโตกส์เป็นชุดของสมการเชิงอนุพันธ์ย่อย (PDE) ซึ่งอธิบายการไหลของของไหลได้เป็นอย่างดี และเป็นจุดเริ่มต้นของเรา พวกเขาสามารถได้มาจากมวล โมเมนตัม และกฎการอนุรักษ์พลังงานที่โยนผ่านทฤษฎีบทการขนส่งเรย์โนลด์ส และใช้ทฤษฎีบทของเกาส์และเรียกใช้สมมติฐานของสโต๊ค สมการต้องใช้สมมติฐานแบบต่อเนื่อง โดยจะถือว่าเรามีอนุภาคของไหลเพียงพอที่จะให้คุณสมบัติทางสถิติ เช่น อุณหภูมิ ความหนาแน่น และความหมายของความเร็ว นอกจากนี้ ความสัมพันธ์เชิงเส้นตรงระหว่างเทนเซอร์ความเค้นพื้นผิวและเทนเซอร์อัตราความเครียด จำเป็นต้องมีสมมาตรในเทนเซอร์ความเค้น และสมมติฐานของไหลไอโซทรอปิก สิ่งสำคัญคือต้องทราบสมมติฐานที่เราทำและสืบทอดในระหว่างการพัฒนานี้ เพื่อให้เราสามารถประเมินการบังคับใช้ในโค้ดผลลัพธ์ได้ สมการ Navier-Stokes ในสัญกรณ์ Einstein โดยไม่ต้องกังวลใจเพิ่มเติม:

การอนุรักษ์มวล:

การอนุรักษ์โมเมนตัม:

การอนุรักษ์พลังงาน:

โดยที่ความเครียดเบี่ยงเบนคือ:

แม้ว่าโดยทั่วไปแล้วจะควบคุมการไหลของของไหลส่วนใหญ่ในโลกทางกายภาพ แต่ก็ไม่ได้มีประโยชน์โดยตรงมากนัก มีวิธีแก้สมการที่แน่นอนซึ่งเป็นที่รู้จักค่อนข้างน้อย และรางวัล Millennium Prize มูลค่า 1,000,000 ดอลลาร์มีไว้สำหรับใครก็ตามที่สามารถแก้ปัญหาการมีอยู่และความราบรื่นได้ ส่วนที่สำคัญคือ เรามีจุดเริ่มต้นสำหรับการพัฒนาแบบจำลองของเราโดยการตั้งสมมติฐานเพื่อลดความซับซ้อน (เป็นสมการที่ยากที่สุดในฟิสิกส์คลาสสิก)

เพื่อให้สิ่งต่าง ๆ "เรียบง่าย" เราจะใช้ความรู้เฉพาะโดเมนของเราเพื่อสร้างสมมติฐานที่ไม่สามารถบีบอัดได้เกี่ยวกับของไหล และสมมติอุณหภูมิคงที่เพื่อไม่ให้การอนุรักษ์สมการพลังงานซึ่งกลายเป็นสมการความร้อน (แยกส่วน) ตอนนี้เรามีสมการสองสมการ ซึ่งยังคงเป็น PDE แต่ง่ายกว่ามากในขณะที่ยังแก้ปัญหาของไหลจริงจำนวนมากได้

สมการความต่อเนื่อง

สมการโมเมนตัม

ณ จุดนี้ เรามีแบบจำลองทางคณิตศาสตร์ที่ดีสำหรับการไหลของของไหลที่ไม่สามารถบีบอัดได้ (เช่น แก๊สความเร็วต่ำและของเหลว เช่น น้ำ) การแก้สมการเหล่านี้โดยตรงด้วยมือไม่ใช่เรื่องง่าย แต่เป็นการดีที่เราจะได้รับคำตอบที่ "แน่นอน" สำหรับปัญหาง่ายๆ การใช้สมการเหล่านี้เพื่อแก้ไขปัญหาที่น่าสนใจ เช่น อากาศที่ไหลผ่านปีก หรือน้ำที่ไหลผ่านระบบบางระบบ กำหนดให้เราต้องแก้สมการเหล่านี้ด้วยตัวเลข

การสร้างแบบแผนตัวเลข

เพื่อที่จะแก้ปัญหาที่ซับซ้อนมากขึ้นโดยใช้คอมพิวเตอร์ จำเป็นต้องมีวิธีการแก้สมการที่บีบอัดไม่ได้ในเชิงตัวเลข การแก้สมการเชิงอนุพันธ์ย่อย หรือแม้แต่สมการเชิงอนุพันธ์ ทางตัวเลขไม่ใช่เรื่องเล็กน้อย อย่างไรก็ตาม สมการของเราในคู่มือนี้มีความท้าทายเป็นพิเศษ (น่าประหลาดใจ!) นั่นคือเราจำเป็นต้องแก้สมการโมเมนตัมในขณะที่รักษาความเป็นอิสระของโซลูชันไว้ตามความต่อเนื่อง การรวมเวลาอย่างง่ายผ่านวิธี Runge-Kutta นั้นทำได้ยากเนื่องจากสมการความต่อเนื่องไม่มีอนุพันธ์ของเวลาอยู่ภายใน

ไม่มีวิธีการแก้สมการที่ถูกต้องหรือแม้แต่ดีที่สุด แต่มีตัวเลือกที่ใช้การได้มากมาย ตลอดหลายทศวรรษที่ผ่านมาพบว่ามีหลายวิธีในการแก้ไขปัญหา เช่น การปรับรูปแบบใหม่ในแง่ของกระแสน้ำวนและฟังก์ชันสตรีม การแนะนำการบีบอัดแบบเทียม และการแยกส่วนของผู้ปฏิบัติงาน Chorin (1969) และจากนั้น Kim and Moin (1984, 1990) ได้กำหนดวิธีการขั้นตอนเศษส่วนที่ประสบความสำเร็จและเป็นที่นิยมอย่างมาก ซึ่งจะช่วยให้เราสามารถรวมสมการในขณะที่แก้สมการสำหรับสนามความดันได้โดยตรง แทนที่จะโดยปริยาย วิธีขั้นตอนเศษส่วนเป็นวิธีการทั่วไปสำหรับการประมาณสมการโดยการแยกตัวดำเนินการออก ในกรณีนี้คือการแยกตามแรงดัน แนวทางนี้ค่อนข้างเรียบง่ายแต่แข็งแกร่ง กระตุ้นให้เกิดทางเลือกที่นี่

อันดับแรก เราต้องแยกแยะสมการเป็นตัวเลขในเวลาเพื่อที่เราจะได้ก้าวจากจุดหนึ่งไปยังอีกจุดหนึ่ง ในการติดตาม Kim และ Moin (1984) เราจะใช้วิธี Adams-Bashforth อันดับสองที่ชัดเจนสำหรับเงื่อนไขการพาความร้อน วิธี Crank-Nicholson อันดับสองโดยปริยายสำหรับเงื่อนไขหนืด ความแตกต่างที่แน่นอนอย่างง่ายสำหรับอนุพันธ์เวลา ในขณะที่ละเลยการไล่ระดับความดัน ตัวเลือกเหล่านี้ไม่ได้เป็นเพียงการประมาณค่าเดียวที่สามารถทำได้: การเลือกนั้นเป็นส่วนหนึ่งของศิลปะในการสร้างโครงร่างโดยการควบคุมพฤติกรรมเชิงตัวเลขของโครงร่าง

ความเร็วระดับกลางสามารถรวมเข้าด้วยกันได้ อย่างไรก็ตาม มันไม่คำนึงถึงการสนับสนุนของแรงดัน และขณะนี้มีความแตกต่างกัน ส่วนที่เหลือของผู้ดำเนินการจำเป็นต้องนำเราไปสู่ขั้นตอนต่อไป

ที่ไหน เป็นสเกลาร์บางตัวที่เราต้องหาว่าผลลัพธ์ใดเป็นความเร็วอิสระแบบไดเวอร์เจนซ์ เราหาได้ โดยการทำไดเวอร์เจนซ์ของขั้นตอนการแก้ไข

โดยที่เทอมแรกเป็นศูนย์ตามที่กำหนดโดยความต่อเนื่อง ให้สมการปัวซองสำหรับสนามสเกลาร์ซึ่งจะให้ความเร็วโซลินอยด์ (ปราศจากไดเวอร์เจนต์) ในขั้นตอนต่อไป

ดังที่ Kim and Moin (1984) แสดงให้เห็น ไม่ใช่ความดันที่เกิดจากการแยกตัวดำเนินการ แต่สามารถพบได้โดย

ณ จุดนี้ในบทช่วยสอน เราทำได้ดีทีเดียว เราได้แยกแยะสมการการปกครองชั่วคราวเพื่อที่เราจะรวมเข้าด้วยกัน ตอนนี้เราจำเป็นต้องแยกแยะตัวดำเนินการตามพื้นที่ มีหลายวิธีที่เราสามารถทำได้ เช่น วิธี Finite Element วิธี Finite Volume และวิธีการ Finite Difference เป็นต้น ในงานต้นฉบับของ Kim and Moin (1984) พวกเขาดำเนินการด้วย Finite Difference Method วิธีการนี้เป็นประโยชน์สำหรับความเรียบง่ายสัมพัทธ์และประสิทธิภาพในการคำนวณ แต่จะทนทุกข์กับรูปทรงที่ซับซ้อนเนื่องจากต้องใช้ตาข่ายที่มีโครงสร้าง

Finite Element Method (FEM) เป็นตัวเลือกที่สะดวกสำหรับเรื่องทั่วไปและมีโครงการโอเพ่นซอร์สที่ดีมากที่ช่วยในการใช้งาน โดยเฉพาะอย่างยิ่ง จะจัดการกับรูปทรงจริงในหนึ่ง สอง และสามมิติ ปรับขนาดสำหรับปัญหาที่ใหญ่มากในคลัสเตอร์เครื่องจักร และค่อนข้างใช้งานง่ายสำหรับองค์ประกอบที่มีลำดับสูง โดยปกติวิธีการนี้จะช้ากว่าในสามวิธี แต่จะทำให้เราเข้าใจปัญหาได้มากที่สุด ดังนั้นเราจะใช้ที่นี่

แม้จะใช้งาน FEM ก็มีตัวเลือกมากมาย ที่นี่เราจะใช้ Galerkin FEM ในการทำเช่นนั้น เราใส่สมการในรูปเศษเหลือถ่วงน้ำหนักโดยคูณแต่ละตัวด้วยฟังก์ชันทดสอบ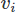 สำหรับเวกเตอร์และ 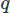สำหรับสนามสเกลาร์และการรวมเข้ากับโดเมน 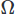. จากนั้นเราจะทำการบูรณาการบางส่วนกับอนุพันธ์อันดับสูงใดๆ โดยใช้ทฤษฎีบทของสโต๊คหรือทฤษฎีบทไดเวอร์เจนซ์ จากนั้นเราก่อให้เกิดปัญหาการแปรผัน โดยได้รูปแบบ CFD ที่ต้องการ

ตอนนี้เรามีแบบแผนทางคณิตศาสตร์ที่ดีในรูปแบบที่ "สะดวก" สำหรับการนำไปใช้ หวังว่าคงจะพอเข้าใจบ้างแล้วว่าอะไรที่จำเป็นเพื่อไปถึงจุดนั้น (คณิตศาสตร์จำนวนมาก และวิธีการจากนักวิจัยที่เก่งกาจที่เราคัดลอกและปรับแต่งมามาก)