Un guide du calcul scientifique avec des outils open source

Historiquement, la science computationnelle a été largement confinée au domaine des chercheurs et des doctorants. Cependant, au fil des ans - peut-être à l'insu de la communauté des logiciels au sens large - nous, les têtes d'œufs de l'informatique scientifique, avons compilé tranquillement des bibliothèques open source collaboratives qui gèrent la grande majorité du travail lourd . Le résultat est qu'il est maintenant plus facile que jamais de mettre en œuvre des modèles mathématiques, et bien que le domaine ne soit peut-être pas encore prêt pour la consommation de masse, la barre d'une mise en œuvre réussie a été considérablement réduite. Développer une nouvelle base de code de calcul à partir de zéro est une entreprise énorme, qui se mesure généralement en années, mais ces projets de calcul scientifique open source permettent de fonctionner avec des exemples accessibles pour exploiter relativement rapidement ces capacités de calcul.

Étant donné que le but du calcul scientifique est de fournir un aperçu scientifique des systèmes réels qui existent dans la nature, la discipline représente l'avant-garde de la concrétisation de l'approche logicielle. Afin de créer des logiciels qui imitent le monde réel à un très haut degré de précision et de résolution, des mathématiques différentielles complexes doivent être invoquées, nécessitant des connaissances rarement trouvées au-delà des murs des universités, des laboratoires nationaux ou des départements de R&D des entreprises. En plus de cela, des défis numériques importants se présentent lorsque l'on tente de décrire le tissu continu et infinitésimal du monde réel en utilisant le langage discret des zéros et des uns. Un effort exhaustif de transformation numérique soigneuse est nécessaire pour rendre des algorithmes qui sont à la fois calculables et qui donnent des résultats significatifs. En d'autres termes, le calcul scientifique est lourd.

Outils open source pour le calcul scientifique

Personnellement, j'aime particulièrement le projet FEniCS, l'utilisant pour mon travail de thèse, et démontrerai mon parti pris en le sélectionnant pour notre exemple de code pour ce tutoriel. (Il existe d'autres projets de très haute qualité tels que DUNE que l'on pourrait également utiliser.)

FEniCS se décrit comme "un projet collaboratif pour le développement de concepts et d'outils innovants pour le calcul scientifique automatisé, avec un accent particulier sur la résolution automatisée d'équations différentielles par des méthodes d'éléments finis". Il s'agit d'une bibliothèque puissante pour résoudre un large éventail de problèmes et d'applications de calcul scientifique. Ses contributeurs incluent Simula Research Laboratory, l'Université de Cambridge, l'Université de Chicago, l'Université Baylor et le KTH Royal Institute of Technology, qui l'ont collectivement construit en une ressource inestimable au cours de la dernière décennie (voir le FEniCS codeswarm).

Ce qui est plutôt étonnant, c'est à quel point la bibliothèque FEniCS nous a protégés des efforts. Pour avoir une idée de la profondeur et de l'étendue étonnantes des sujets couverts par le projet, vous pouvez consulter leur manuel open source, où le chapitre 21 compare même divers schémas d'éléments finis pour résoudre des flux incompressibles.

Dans les coulisses, le projet a intégré pour nous un large ensemble de bibliothèques de calcul scientifique open source, qui peuvent être intéressantes ou directement utilisables. Ceux-ci incluent, sans ordre particulier, les projets que le projet FEniCS appelle :

• PETSc : une suite de structures de données et de routines pour la solution évolutive (parallèle) d'applications scientifiques modélisées par des équations aux dérivées partielles.
• Projet Trilinos : Un ensemble d'algorithmes et de technologies robustes pour résoudre des équations linéaires et non linéaires, développé à partir des travaux de Sandia National Labs.
• uBLAS : "Une bibliothèque de classes de modèles C++ qui fournit des fonctionnalités BLAS de niveau 1, 2, 3 pour les matrices denses, compactes et clairsemées et de nombreux algorithmes numériques pour l'algèbre linéaire."
• GMP : une bibliothèque gratuite pour l'arithmétique de précision arbitraire, fonctionnant sur des nombres entiers signés, des nombres rationnels et des nombres à virgule flottante.
• UMFPACK : Un ensemble de routines pour résoudre des systèmes linéaires creux asymétriques, Ax=b, en utilisant la méthode Unsymmetric MultiFrontal.
• ParMETIS : une bibliothèque parallèle basée sur MPI qui implémente une variété d'algorithmes pour partitionner des graphes non structurés, des maillages et pour calculer des ordres de réduction de remplissage de matrices creuses.
• NumPy : le package fondamental pour le calcul scientifique avec Python.
• CGAL : Algorithmes géométriques efficaces et fiables sous la forme d'une bibliothèque C++.
• SCOTCH : un progiciel et des bibliothèques pour le partitionnement de graphes séquentiels et parallèles, le mappage et le clustering statiques, le partitionnement séquentiel de maillage et d'hypergraphes et l'ordonnancement séquentiel et parallèle de blocs de matrice clairsemée.
• MPI : Un système de transmission de messages standardisé et portable conçu par un groupe de chercheurs du milieu universitaire et de l'industrie pour fonctionner sur une grande variété d'ordinateurs parallèles.
• VTK : Un système logiciel open-source et disponible gratuitement pour l'infographie 3D, le traitement et la visualisation d'images.
• SLEPc : une bibliothèque de logiciels pour la résolution de problèmes de valeurs propres creuses à grande échelle sur des ordinateurs parallèles.

Cette liste de packages externes intégrés au projet nous donne une idée de ses capacités héritées. Par exemple, la prise en charge intégrée de MPI permet une mise à l'échelle entre les travailleurs distants dans un environnement de cluster de calcul (c'est-à-dire que ce code s'exécutera sur un super ordinateur ou sur votre ordinateur portable).

Il est également intéressant de noter qu'il existe de nombreuses applications au-delà du calcul scientifique pour lesquelles ces projets pourraient être utilisés, notamment la modélisation financière, le traitement d'images, les problèmes d'optimisation et peut-être même les jeux vidéo. Il serait possible, par exemple, de créer un jeu vidéo qui utilise certains de ces algorithmes et techniques open source pour résoudre un écoulement de fluide bidimensionnel, tel que celui des courants océaniques / fluviaux avec lesquels un joueur interagirait (peut-être essayer et faire naviguer un bateau avec des vents et des débits d'eau variables).

Un exemple d'application : tirer parti de l'open source pour le calcul scientifique

Ici, je vais essayer de donner une idée de ce qu'implique le développement d'un modèle numérique en montrant comment un schéma de base de dynamique des fluides computationnelle est développé et implémenté dans l'une de ces bibliothèques open source - dans ce cas, le projet FEniCS. FEnICS fournit des API en Python et C++. Pour cet exemple, nous utiliserons leur API Python.

Nous aborderons un contenu plutôt technique, mais l'objectif sera simplement de donner un avant-goût de ce qu'implique le développement d'un tel code de calcul scientifique, et à quel point les outils open source d'aujourd'hui font pour nous. Dans le processus, nous espérons aider à démystifier le monde complexe du calcul scientifique. (Notez qu'une annexe est fournie qui détaille tous les fondements mathématiques et scientifiques pour ceux qui sont intéressés par ce niveau de détail.)

AVIS DE NON-RESPONSABILITÉ : Pour les lecteurs ayant peu ou pas d'expérience dans les logiciels et les applications de calcul scientifique, certaines parties de cet exemple peuvent vous faire ressentir ceci :

Si oui, ne désespérez pas. Le principal point à retenir ici est la mesure dans laquelle les projets open source existants peuvent grandement simplifier bon nombre de ces tâches.

Dans cet esprit, commençons par regarder la démo FEnICS pour Navier-Stokes incompressible. Cette démo modélise la pression et la vitesse d'un fluide incompressible circulant dans un coude en forme de L, tel qu'un tuyau de plomberie.

La description sur la page de démonstration liée donne une excellente configuration concise des étapes nécessaires à l'exécution du code, et je vous encourage à jeter un coup d'œil rapide pour voir ce qui est impliqué. Pour résumer, la démo résoudra la vitesse et la pression à travers le coude pour les équations d'écoulement incompressibles. La démo exécute une courte simulation du fluide qui s'écoule au fil du temps, animant les résultats au fur et à mesure. Ceci est accompli en configurant le maillage représentant l'espace dans le tuyau et en utilisant la méthode des éléments finis pour résoudre numériquement la vitesse et la pression à chaque point du maillage. Nous parcourons ensuite le temps, mettant à jour les champs de vitesse et de pression au fur et à mesure, en utilisant à nouveau les équations dont nous disposons.

La démo fonctionne bien telle quelle, mais nous allons la modifier légèrement. La démo utilise la division Chorin, mais nous allons utiliser à la place la méthode légèrement différente inspirée de Kim et Moin, qui, nous l'espérons, est plus stable. Cela nous oblige simplement à changer l'équation utilisée pour approximer les termes convectifs et visqueux, mais pour ce faire, nous devons stocker le champ de vitesse du pas de temps précédent et ajouter deux termes supplémentaires à l'équation de mise à jour, qui utilisera ce précédent. informations pour une approximation numérique plus précise.

Alors faisons ce changement. Tout d'abord, nous ajoutons un nouvel objet Function à la configuration. Il s'agit d'un objet qui représente une fonction mathématique abstraite telle qu'un vecteur ou un champ scalaire. Nous l'appellerons un1 il stockera le champ de vitesse précédent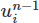 sur notre espace fonctionnel V .

 ... # Create functions (three distinct vector fields and a scalar field) un1 = Function(V) # the previous time step's velocity field we are adding u0 = Function(V) # the current velocity field u1 = Function(V) # the next velocity field (what's being solved for) p1 = Function(Q) # the next pressure field (what's being solved for) ...

Ensuite, nous devons changer la façon dont la "vitesse provisoire" est mise à jour à chaque étape de la simulation. Ce champ représente la vitesse approximative au prochain pas de temps lorsque la pression est ignorée (à ce stade, la pression n'est pas encore connue). C'est ici que nous remplaçons la méthode de fractionnement de Chorin par la méthode plus récente des étapes fractionnaires de Kim et Moin. En d'autres termes, nous allons changer l'expression du champ F1 :

Remplacer:

 # Tentative velocity field (a first prediction of what the next velocity field is) # for the Chorin style split # F1 = change in the velocity field + # convective term + # diffusive term - # body force term F1 = (1/k)*inner(u - u0, v)*dx + \ inner(grad(u0)*u0, v)*dx + \ nu*inner(grad(u), grad(v))*dx - \ inner(f, v)*dx

Avec:

 # Tentative velocity field (a first prediction of what the next velocity field is) # for the Kim and Moin style split # F1 = change in the velocity field + # convective term + # diffusive term - # body force term F1 = (1/k)*inner(u - u0, v)*dx + \ (3.0/2.0) * inner(grad(u0)*u0, v)*dx - (1.0/2.0) * inner(grad(un1)*un1, v)*dx + \ (nu/2.0)*inner(grad(u+u0), grad(v))*dx - \ inner(f, v)*dx

de sorte que la démo utilise maintenant notre méthode mise à jour pour résoudre le champ de vitesse intermédiaire lorsqu'elle utilise F1 .

Enfin, assurez-vous que nous mettons à jour le champ de vitesse précédent, un1 , à la fin de chaque étape d'itération

 ... # Move to next time step un1.assign(u0) # copy the current velocity field into the previous velocity field u0.assign(u1) # copy the next velocity field into the current velocity field ...

Ainsi, voici le code complet de notre démo FEniCS CFD, avec nos modifications incluses :

 """This demo program solves the incompressible Navier-Stokes equations on an L-shaped domain using Kim and Moin's fractional step method.""" # Begin demo from dolfin import * # Print log messages only from the root process in parallel parameters["std_out_all_processes"] = False; # Load mesh from file mesh = Mesh("lshape.xml.gz") # Define function spaces (P2-P1) V = VectorFunctionSpace(mesh, "Lagrange", 2) Q = FunctionSpace(mesh, "Lagrange", 1) # Define trial and test functions u = TrialFunction(V) p = TrialFunction(Q) v = TestFunction(V) q = TestFunction(Q) # Set parameter values dt = 0.01 T = 3 nu = 0.01 # Define time-dependent pressure boundary condition p_in = Expression("sin(3.0*t)", t=0.0) # Define boundary conditions noslip = DirichletBC(V, (0, 0), "on_boundary && \ (x[0] < DOLFIN_EPS | x[1] < DOLFIN_EPS | \ (x[0] > 0.5 - DOLFIN_EPS && x[1] > 0.5 - DOLFIN_EPS))") inflow = DirichletBC(Q, p_in, "x[1] > 1.0 - DOLFIN_EPS") outflow = DirichletBC(Q, 0, "x[0] > 1.0 - DOLFIN_EPS") bcu = [noslip] bcp = [inflow, outflow] # Create functions un1 = Function(V) u0 = Function(V) u1 = Function(V) p1 = Function(Q) # Define coefficients k = Constant(dt) f = Constant((0, 0)) # Tentative velocity field (a first prediction of what the next velocity field is) # for the Kim and Moin style split # F1 = change in the velocity field + # convective term + # diffusive term - # body force term F1 = (1/k)*inner(u - u0, v)*dx + \ (3.0/2.0) * inner(grad(u0)*u0, v)*dx - (1.0/2.0) * inner(grad(un1)*un1, v)*dx + \ (nu/2.0)*inner(grad(u+u0), grad(v))*dx - \ inner(f, v)*dx a1 = lhs(F1) L1 = rhs(F1) # Pressure update a2 = inner(grad(p), grad(q))*dx L2 = -(1/k)*div(u1)*q*dx # Velocity update a3 = inner(u, v)*dx L3 = inner(u1, v)*dx - k*inner(grad(p1), v)*dx # Assemble matrices A1 = assemble(a1) A2 = assemble(a2) A3 = assemble(a3) # Use amg preconditioner if available prec = "amg" if has_krylov_solver_preconditioner("amg") else "default" # Create files for storing solution ufile = File("results/velocity.pvd") pfile = File("results/pressure.pvd") # Time-stepping t = dt while t < T + DOLFIN_EPS: # Update pressure boundary condition p_in.t = t # Compute tentative velocity step begin("Computing tentative velocity") b1 = assemble(L1) [bc.apply(A1, b1) for bc in bcu] solve(A1, u1.vector(), b1, "gmres", "default") end() # Pressure correction begin("Computing pressure correction") b2 = assemble(L2) [bc.apply(A2, b2) for bc in bcp] solve(A2, p1.vector(), b2, "cg", prec) end() # Velocity correction begin("Computing velocity correction") b3 = assemble(L3) [bc.apply(A3, b3) for bc in bcu] solve(A3, u1.vector(), b3, "gmres", "default") end() # Plot solution plot(p1, title="Pressure", rescale=True) plot(u1, title="Velocity", rescale=True) # Save to file ufile << u1 pfile << p1 # Move to next time step un1.assign(u0) u0.assign(u1) t += dt print "t =", t # Hold plot interactive()

L'exécution du programme montre le flux autour du coude. Exécutez vous-même le code de calcul scientifique pour le voir s'animer ! Les écrans de la trame finale sont présentés ci-dessous.

Pressions relatives dans le virage à la fin de la simulation, mises à l'échelle et colorées par amplitude (valeurs non dimensionnelles) :

Vitesses relatives dans le virage à la fin de la simulation sous forme de glyphes vectoriels mis à l'échelle et colorés par amplitude (valeurs non dimensionnelles).

Nous avons donc pris une démo existante, qui implémente assez facilement un schéma très similaire au nôtre, et l'avons modifié pour utiliser de meilleures approximations en utilisant les informations du pas de temps précédent.

À ce stade, vous pensez peut-être qu'il s'agissait d'une modification triviale. C'était le cas, et c'est en grande partie le but. Ce projet de calcul scientifique open source nous a permis d'implémenter rapidement un modèle numérique modifié en changeant quatre lignes de code. De tels changements peuvent prendre des mois dans les grands codes de recherche.

Le projet a de nombreuses autres démos qui pourraient être utilisées comme point de départ. Il existe même un certain nombre d'applications open source construites sur le projet qui implémentent divers modèles.

Conclusion

Le calcul scientifique et ses applications sont en effet complexes. Il n'y a pas moyen de contourner cela. Mais comme c'est de plus en plus vrai dans de nombreux domaines, le paysage toujours croissant d'outils et de projets open source disponibles peut considérablement simplifier ce qui serait autrement des tâches de programmation extrêmement compliquées et fastidieuses. Et peut-être que le temps est même proche où l'informatique scientifique devient suffisamment accessible pour se retrouver facilement utilisée au-delà de la communauté de la recherche.

ANNEXE : fondements scientifiques et mathématiques

Pour les personnes intéressées, voici les fondements techniques de notre guide sur la dynamique des fluides computationnelle ci-dessus. Ce qui suit servira de résumé très utile et concis des sujets qui sont généralement couverts au cours d'une douzaine de cours de niveau supérieur. Les étudiants diplômés et les types mathématiques intéressés par une compréhension approfondie du sujet peuvent trouver ce matériel très intéressant.

Mécanique des fluides

La "modélisation", en général, est le processus de résolution d'un système réel avec une série d'approximations. Le modèle impliquera souvent des équations continues mal adaptées à la mise en œuvre informatique et doit donc être davantage approchée avec des méthodes numériques.

Pour la mécanique des fluides, commençons ce guide par les équations fondamentales, les équations de Navier-Stokes, et utilisons-les pour développer un schéma CFD.

Les équations de Navier-Stokes sont une série d'équations aux dérivées partielles (EDP) qui décrivent très bien les écoulements de fluides et sont donc notre point de départ. Ils peuvent être dérivés des lois de conservation de la masse, de la quantité de mouvement et de l'énergie lancées à travers un théorème de transport de Reynolds et en appliquant le théorème de Gauss et en invoquant l'hypothèse de Stoke. Les équations nécessitent une hypothèse de continuum, où l'on suppose que nous avons suffisamment de particules de fluide pour donner des propriétés statistiques telles que la signification de la température, de la densité et de la vitesse. De plus, une relation linéaire entre le tenseur de contrainte de surface et le tenseur de vitesse de déformation, la symétrie dans le tenseur de contrainte et les hypothèses de fluide isotrope sont nécessaires. Il est important de connaître les hypothèses que nous faisons et héritons au cours de ce développement afin que nous puissions évaluer l'applicabilité dans le code résultant. Les équations de Navier-Stokes en notation Einstein, sans plus tarder :

Conservation de la masse:

Conservation de la quantité de mouvement :

Conservation d'énergie:

où la contrainte déviatorique est :

Bien que très généraux, régissant la plupart des flux de fluides dans le monde physique, ils ne sont pas directement d'une grande utilité. Il existe relativement peu de solutions exactes connues aux équations, et un prix du millénaire de 1 000 000 $ est disponible pour quiconque peut résoudre le problème de l'existence et de la régularité. La partie importante est que nous avons un point de départ pour le développement de notre modèle en faisant une série d'hypothèses pour réduire la complexité (ce sont certaines des équations les plus difficiles de la physique classique).

Pour garder les choses «simples», nous utiliserons nos connaissances spécifiques au domaine pour faire une hypothèse incompressible sur le fluide et supposer des températures constantes telles que l'équation de conservation de l'énergie, qui devient l'équation de la chaleur, n'est pas nécessaire (découplée). Nous avons maintenant deux équations, toujours des EDP, mais nettement plus simples tout en résolvant un grand nombre de problèmes fluides réels.

Équation de continuité

Équations de quantité de mouvement

À ce stade, nous avons maintenant un joli modèle mathématique pour les écoulements de fluides incompressibles (gaz à faible vitesse et liquides comme l'eau, par exemple). Résoudre ces équations directement à la main n'est pas facile, mais c'est bien dans la mesure où nous pouvons obtenir des solutions «exactes» pour des problèmes simples. L'utilisation de ces équations pour résoudre des problèmes d'intérêt, par exemple l'air circulant sur une aile ou l'eau circulant dans un système, nécessite que nous résolvions ces équations numériquement.

Construire un schéma numérique

Afin de résoudre des problèmes plus complexes à l'aide de l'ordinateur, une méthode pour résoudre numériquement nos équations incompressibles est nécessaire. Résoudre numériquement des équations aux dérivées partielles, voire des équations aux dérivées, n'est pas anodin. Cependant, nos équations dans ce guide présentent un défi particulier (surprise !). Autrement dit, nous devons résoudre les équations de quantité de mouvement tout en gardant la solution sans divergence, comme l'exige la continuité. Une intégration temporelle simple via quelque chose comme la méthode Runge-Kutta est rendue difficile car l'équation de continuité ne contient pas de dérivée temporelle.

Il n'y a pas de méthode correcte, ni même la meilleure, pour résoudre les équations, mais il existe de nombreuses options réalisables. Au fil des décennies, plusieurs approches ont été trouvées pour résoudre le problème, telles que la reformulation en termes de vorticité et de fonction de flux, l'introduction de la compressibilité artificielle et la division des opérateurs. Chorin (1969), puis Kim et Moin (1984, 1990), ont formulé une méthode d'étape fractionnaire très réussie et populaire qui nous permettra d'intégrer les équations tout en résolvant le champ de pression directement, plutôt qu'implicitement. La méthode de l'étape fractionnaire est une méthode générale d'approximation des équations en divisant leurs opérateurs, dans ce cas en divisant le long de la pression. L'approche est relativement simple et pourtant robuste, motivant ici son choix.

Tout d'abord, nous devons discriminer numériquement les équations dans le temps afin de pouvoir passer d'un point dans le temps au suivant. En suivant Kim et Moin (1984), nous utiliserons la méthode d'Adams-Bashforth explicite du second ordre pour les termes convectifs, la méthode de Crank-Nicholson implicite du second ordre pour les termes visqueux, une simple différence finie pour la dérivée temporelle , en négligeant le gradient de pression. Ces choix ne sont en aucun cas les seules approximations possibles : leur sélection fait partie de l'art de construire le schéma en contrôlant le comportement numérique du schéma.

La vitesse intermédiaire peut maintenant être intégrée, cependant, elle ignore la contribution de la pression et est maintenant divergente (l'incompressibilité exige qu'elle soit libre de divergence). Le reste de l'opérateur est nécessaire pour nous amener au pas de temps suivant.

où est un scalaire que nous devons trouver qui se traduit par une vitesse libre divergente. Nous pouvons trouver en prenant la divergence du pas de correction,

où le premier terme est nul comme l'exige la continuité, donnant une équation de Poisson pour un champ scalaire qui fournira une vitesse solénoïdale (libre divergente) au prochain pas de temps.

Comme le montrent Kim et Moin (1984), n'est pas exactement la pression résultant de la division de l'opérateur, mais elle peut être trouvée par

A ce stade du didacticiel où nous nous débrouillons plutôt bien, nous avons discrité temporellement les équations gouvernantes afin de pouvoir les intégrer. Il faut maintenant discriminer spatialement les opérateurs. Il existe un certain nombre de méthodes avec lesquelles nous pourrions accomplir cela, la méthode des éléments finis, la méthode des volumes finis et la méthode des différences finies, par exemple. Dans le travail original de Kim et Moin (1984), ils procèdent avec la méthode des différences finies. La méthode est avantageuse pour sa simplicité relative et son efficacité de calcul, mais souffre pour les géométries complexes car elle nécessite un maillage structuré.

La méthode des éléments finis (FEM) est une sélection pratique pour sa généralité et a quelques très beaux projets open source aidant à son utilisation. En particulier, il gère des géométries réelles en une, deux et trois dimensions, des échelles pour de très grands problèmes sur des clusters de machines, et est relativement facile à utiliser pour des éléments d'ordre élevé. Généralement, la méthode est la plus lente des trois, mais elle nous donnera le plus de kilométrage à travers les problèmes, nous l'utiliserons donc ici.

Même lors de la mise en œuvre du FEM, il existe de nombreux choix. Ici, nous allons utiliser le Galerkin FEM. Ce faisant, nous jetons les équations sous forme résiduelle pondérée en multipliant chacune par une fonction de test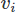 pour les vecteurs et 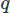pour le champ scalaire, et intégrant sur le domaine 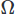. Nous effectuons ensuite une intégration partielle sur toutes les dérivées d'ordre élevé en utilisant le théorème de Stoke ou le théorème de divergence. Nous posons ensuite le problème variationnel, donnant notre schéma CFD souhaité.

Nous avons maintenant un joli schéma mathématique sous une forme "pratique" pour la mise en œuvre, avec une certaine idée de ce qui était nécessaire pour y arriver (beaucoup de mathématiques et de méthodes de brillants chercheurs que nous copions et peaufinons à peu près).