Um guia para computação científica com ferramentas de código aberto

Historicamente, a ciência computacional tem sido amplamente confinada ao domínio dos cientistas pesquisadores e doutorandos. No entanto, ao longo dos anos – talvez sem o conhecimento da comunidade de software maior – nós, cabeças de ovos da computação científica, compilamos silenciosamente bibliotecas colaborativas de código aberto que lidam com a grande maioria do trabalho pesado . O resultado é que agora é mais fácil do que nunca implementar modelos matemáticos e, embora o campo ainda não esteja pronto para o consumo em massa, a barreira para uma implementação bem-sucedida foi drasticamente reduzida. Desenvolver uma nova base de código computacional do zero é um grande empreendimento, medido normalmente em anos, mas esses projetos de computação científica de código aberto estão possibilitando a execução com exemplos acessíveis para alavancar com relativa rapidez essas habilidades computacionais.

Uma vez que o propósito da computação científica é fornecer uma visão científica de sistemas reais que existem na natureza, a disciplina representa a vanguarda em tornar realidade a abordagem de software de computador. Para fazer um software que imite o mundo real em um grau muito alto de precisão e resolução, a matemática diferencial complexa deve ser invocada, exigindo conhecimento que raramente é encontrado além dos muros das universidades, laboratórios nacionais ou departamentos corporativos de P&D. Além disso, desafios numéricos significativos se apresentam ao tentar descrever o tecido contínuo e infinitesimal do mundo real usando a linguagem discreta de zeros e uns. Um esforço exaustivo de transformação numérica cuidadosa é necessário para renderizar algoritmos que sejam computacionalmente tratáveis ​​e que forneçam resultados significativos. Em outras palavras, a computação científica é um trabalho pesado.

Ferramentas de código aberto para computação científica

Pessoalmente, gosto particularmente do projeto FEniCS, usando-o para meu trabalho de tese, e demonstrarei meu viés ao selecioná-lo para nosso exemplo de código para este tutorial. (Existem outros projetos de alta qualidade, como DUNE, que também podem ser usados.)

O FEniCS se autodescreve como “um projeto colaborativo para o desenvolvimento de conceitos e ferramentas inovadoras para computação científica automatizada, com foco particular na solução automatizada de equações diferenciais por métodos de elementos finitos”. Esta é uma biblioteca poderosa para resolver uma enorme variedade de problemas e aplicações de computação científica. Seus colaboradores incluem o Simula Research Laboratory, a Universidade de Cambridge, a Universidade de Chicago, a Baylor University e o KTH Royal Institute of Technology, que coletivamente o transformaram em um recurso inestimável ao longo da última década (veja o codewarm FEniCS).

O que é surpreendente é o quanto de esforço a biblioteca FEniCS nos protegeu. Para ter uma noção da incrível profundidade e amplitude dos tópicos que o projeto cobre, pode-se ver o livro-texto de código aberto, onde o Capítulo 21 compara vários esquemas de elementos finitos para resolver fluxos incompressíveis.

Nos bastidores, o projeto integrou para nós um grande conjunto de bibliotecas de computação científica de código aberto, que podem ser de interesse ou de uso direto. Estes incluem, em nenhuma ordem particular, os projetos que o projeto FEniCS chama:

• PETSc: Um conjunto de estruturas de dados e rotinas para a solução escalável (paralela) de aplicações científicas modeladas por equações diferenciais parciais.
• Projeto Trilinos: Um conjunto de algoritmos e tecnologias robustos para resolver equações lineares e não lineares, desenvolvido a partir do trabalho no Sandia National Labs.
• uBLAS: “Uma biblioteca de classes de modelo C++ que fornece funcionalidade BLAS nível 1, 2, 3 para matrizes densas, compactadas e esparsas e muitos algoritmos numéricos para álgebra linear.”
• GMP: Uma biblioteca gratuita para aritmética de precisão arbitrária, operando em inteiros com sinal, números racionais e números de ponto flutuante.
• UMFPACK: Um conjunto de rotinas para resolver sistemas lineares esparsos assimétricos, Ax=b, usando o método Unsymmetric MultiFrontal.
• ParMETIS: Uma biblioteca paralela baseada em MPI que implementa uma variedade de algoritmos para particionar grafos não estruturados, malhas e para computar ordenações de redução de preenchimento de matrizes esparsas.
• NumPy: O pacote fundamental para computação científica com Python.
• CGAL: Algoritmos geométricos eficientes e confiáveis ​​na forma de uma biblioteca C++.
• SCOTCH: Um pacote de software e bibliotecas para particionamento de grafos sequenciais e paralelos, mapeamento estático e clustering, particionamento de malha sequencial e hipergrafo e ordenação de blocos de matriz esparsa sequencial e paralela.
• MPI: Um sistema de passagem de mensagens padronizado e portátil projetado por um grupo de pesquisadores da academia e da indústria para funcionar em uma ampla variedade de computadores paralelos.
• VTK: Um sistema de software de código aberto e disponível gratuitamente para computação gráfica 3D, processamento e visualização de imagens.
• SLEPc: Uma biblioteca de software para a solução de problemas de autovalores esparsos em larga escala em computadores paralelos.

Esta lista de pacotes externos integrados ao projeto nos dá uma noção de suas capacidades herdadas. Por exemplo, ter suporte integrado para MPI permite dimensionar entre trabalhadores remotos em um ambiente de cluster de computação (ou seja, esse código será executado em um supercomputador ou laptop).

Também é interessante notar que existem muitas aplicações além da computação científica para as quais esses projetos podem ser utilizados, incluindo modelagem financeira, processamento de imagens, problemas de otimização e talvez até videogames. Seria possível, por exemplo, criar um videogame que usasse alguns desses algoritmos e técnicas de código aberto para resolver um fluxo de fluido bidimensional, como o de correntes oceânicas / fluviais com as quais um jogador interagiria (talvez tentar e navegar um barco com ventos variados e fluxos de água).

Um exemplo de aplicativo: aproveitando o código aberto para computação científica

Aqui tentarei dar uma ideia do que o desenvolvimento de um modelo numérico envolve, mostrando como um esquema básico de Dinâmica de Fluidos Computacional é desenvolvido e implementado em uma dessas bibliotecas de código aberto - neste caso, o projeto FEniCS. O FEnICS fornece APIs em Python e C++. Para este exemplo, usaremos sua API Python.

Discutiremos algum conteúdo bastante técnico, mas o objetivo será simplesmente dar uma amostra do que o desenvolvimento de tal código de computação científica implica, e quanto trabalho braçal as ferramentas de código aberto de hoje fazem por nós. No processo, esperamos ajudar a desmistificar o complexo mundo da computação científica. (Observe que é fornecido um apêndice que detalha todos os fundamentos matemáticos e científicos para aqueles que estão interessados ​​nesse nível de detalhe.)

ISENÇÃO DE RESPONSABILIDADE: Para aqueles leitores com pouco ou nenhum conhecimento em software e aplicativos de computação científica, partes deste exemplo podem fazer você se sentir assim:

Se sim, não se desespere. A principal conclusão aqui é até que ponto os projetos de código aberto existentes podem simplificar bastante muitas dessas tarefas.

Com isso em mente, vamos começar analisando a demonstração do FEnICS para Navier-Stokes incompressíveis. Esta demonstração modela a pressão e a velocidade de um fluido incompressível que flui através de uma curva em forma de L, como um tubo de encanamento.

A descrição na página de demonstração vinculada fornece uma configuração excelente e concisa das etapas necessárias para executar o código, e recomendo que você dê uma olhada rápida para ver o que está envolvido. Para resumir, a demonstração resolverá a velocidade e a pressão através da curva para as equações de fluxo incompressíveis. A demonstração executa uma breve simulação do fluido fluindo ao longo do tempo, animando os resultados à medida que avança. Isso é feito configurando a malha que representa o espaço no tubo e usando o Método dos Elementos Finitos para resolver numericamente a velocidade e a pressão em cada ponto da malha. Em seguida, iteramos no tempo, atualizando os campos de velocidade e pressão à medida que avançamos, novamente usando as equações que temos à nossa disposição.

A demonstração funciona bem como está, mas vamos modificá-la um pouco. A demo usa a divisão Chorin, mas vamos usar o método ligeiramente diferente inspirado em Kim e Moin, que esperamos que seja mais estável. Isso requer apenas que mudemos a equação usada para aproximar os termos convectivos e viscosos, mas para isso precisamos armazenar o campo de velocidade do passo de tempo anterior e adicionar dois termos adicionais à equação de atualização, que usará o anterior informações para uma aproximação numérica mais precisa.

Então vamos fazer essa mudança. Primeiro, adicionamos um novo objeto Function ao setup. Este é um objeto que representa uma função matemática abstrata, como um vetor ou campo escalar. Vamos chamá-lo de un1 , ele armazenará o campo de velocidade anterior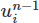 em nosso espaço de função V .

 ... # Create functions (three distinct vector fields and a scalar field) un1 = Function(V) # the previous time step's velocity field we are adding u0 = Function(V) # the current velocity field u1 = Function(V) # the next velocity field (what's being solved for) p1 = Function(Q) # the next pressure field (what's being solved for) ...

Em seguida, precisamos alterar a forma como a “velocidade provisória” é atualizada durante cada etapa da simulação. Este campo representa a velocidade aproximada no próximo passo de tempo quando a pressão é ignorada (neste ponto a pressão ainda não é conhecida). É aqui que substituímos o método de divisão de Chorin pelo método de passo fracionário mais recente de Kim e Moin. Em outras palavras, vamos mudar a expressão para o campo F1 :

Substituir:

 # Tentative velocity field (a first prediction of what the next velocity field is) # for the Chorin style split # F1 = change in the velocity field + # convective term + # diffusive term - # body force term F1 = (1/k)*inner(u - u0, v)*dx + \ inner(grad(u0)*u0, v)*dx + \ nu*inner(grad(u), grad(v))*dx - \ inner(f, v)*dx

Com:

 # Tentative velocity field (a first prediction of what the next velocity field is) # for the Kim and Moin style split # F1 = change in the velocity field + # convective term + # diffusive term - # body force term F1 = (1/k)*inner(u - u0, v)*dx + \ (3.0/2.0) * inner(grad(u0)*u0, v)*dx - (1.0/2.0) * inner(grad(un1)*un1, v)*dx + \ (nu/2.0)*inner(grad(u+u0), grad(v))*dx - \ inner(f, v)*dx

para que a demonstração agora use nosso método atualizado para resolver o campo de velocidade intermediário ao usar F1 .

Finalmente, certifique-se de que estamos atualizando o campo de velocidade anterior, un1 , no final de cada etapa de iteração

 ... # Move to next time step un1.assign(u0) # copy the current velocity field into the previous velocity field u0.assign(u1) # copy the next velocity field into the current velocity field ...

Para que o seguinte seja o código completo da nossa demonstração FEniCS CFD, com nossas alterações incluídas:

 """This demo program solves the incompressible Navier-Stokes equations on an L-shaped domain using Kim and Moin's fractional step method.""" # Begin demo from dolfin import * # Print log messages only from the root process in parallel parameters["std_out_all_processes"] = False; # Load mesh from file mesh = Mesh("lshape.xml.gz") # Define function spaces (P2-P1) V = VectorFunctionSpace(mesh, "Lagrange", 2) Q = FunctionSpace(mesh, "Lagrange", 1) # Define trial and test functions u = TrialFunction(V) p = TrialFunction(Q) v = TestFunction(V) q = TestFunction(Q) # Set parameter values dt = 0.01 T = 3 nu = 0.01 # Define time-dependent pressure boundary condition p_in = Expression("sin(3.0*t)", t=0.0) # Define boundary conditions noslip = DirichletBC(V, (0, 0), "on_boundary && \ (x[0] < DOLFIN_EPS | x[1] < DOLFIN_EPS | \ (x[0] > 0.5 - DOLFIN_EPS && x[1] > 0.5 - DOLFIN_EPS))") inflow = DirichletBC(Q, p_in, "x[1] > 1.0 - DOLFIN_EPS") outflow = DirichletBC(Q, 0, "x[0] > 1.0 - DOLFIN_EPS") bcu = [noslip] bcp = [inflow, outflow] # Create functions un1 = Function(V) u0 = Function(V) u1 = Function(V) p1 = Function(Q) # Define coefficients k = Constant(dt) f = Constant((0, 0)) # Tentative velocity field (a first prediction of what the next velocity field is) # for the Kim and Moin style split # F1 = change in the velocity field + # convective term + # diffusive term - # body force term F1 = (1/k)*inner(u - u0, v)*dx + \ (3.0/2.0) * inner(grad(u0)*u0, v)*dx - (1.0/2.0) * inner(grad(un1)*un1, v)*dx + \ (nu/2.0)*inner(grad(u+u0), grad(v))*dx - \ inner(f, v)*dx a1 = lhs(F1) L1 = rhs(F1) # Pressure update a2 = inner(grad(p), grad(q))*dx L2 = -(1/k)*div(u1)*q*dx # Velocity update a3 = inner(u, v)*dx L3 = inner(u1, v)*dx - k*inner(grad(p1), v)*dx # Assemble matrices A1 = assemble(a1) A2 = assemble(a2) A3 = assemble(a3) # Use amg preconditioner if available prec = "amg" if has_krylov_solver_preconditioner("amg") else "default" # Create files for storing solution ufile = File("results/velocity.pvd") pfile = File("results/pressure.pvd") # Time-stepping t = dt while t < T + DOLFIN_EPS: # Update pressure boundary condition p_in.t = t # Compute tentative velocity step begin("Computing tentative velocity") b1 = assemble(L1) [bc.apply(A1, b1) for bc in bcu] solve(A1, u1.vector(), b1, "gmres", "default") end() # Pressure correction begin("Computing pressure correction") b2 = assemble(L2) [bc.apply(A2, b2) for bc in bcp] solve(A2, p1.vector(), b2, "cg", prec) end() # Velocity correction begin("Computing velocity correction") b3 = assemble(L3) [bc.apply(A3, b3) for bc in bcu] solve(A3, u1.vector(), b3, "gmres", "default") end() # Plot solution plot(p1, title="Pressure", rescale=True) plot(u1, title="Velocity", rescale=True) # Save to file ufile << u1 pfile << p1 # Move to next time step un1.assign(u0) u0.assign(u1) t += dt print "t =", t # Hold plot interactive()

A execução do programa mostra o fluxo ao redor do cotovelo. Execute você mesmo o código de computação científica para vê-lo animar! As telas do quadro final são apresentadas abaixo.

Pressões relativas na curva no final da simulação, dimensionadas e coloridas por magnitude (valores não dimensionais):

Velocidades relativas na curva no final da simulação como glifos vetoriais dimensionados e coloridos por magnitude (valores não dimensionais).

Então, o que fizemos foi pegar uma demonstração existente, que por acaso implementa um esquema muito semelhante ao nosso com bastante facilidade, e o modificamos para usar melhores aproximações usando informações da etapa de tempo anterior.

Neste ponto, você pode estar pensando que foi uma edição trivial. Foi, e esse é, em grande parte, o ponto. Este projeto de computação científica de código aberto nos permitiu implementar rapidamente um modelo numérico modificado alterando quatro linhas de código. Tais mudanças podem levar meses em grandes códigos de pesquisa.

O projeto tem muitas outras demos que podem ser usadas como ponto de partida. Há até uma série de aplicativos de código aberto construídos no projeto que implementam vários modelos.

Conclusão

A computação científica e suas aplicações são de fato complexas. Não há como contornar isso. Mas, como é cada vez mais verdade em muitos domínios, o cenário cada vez maior de ferramentas e projetos de código aberto disponíveis pode simplificar significativamente o que de outra forma seriam tarefas de programação extremamente complicadas e tediosas. E talvez esteja próximo o momento em que a computação científica se tornará acessível o suficiente para ser prontamente utilizada além da comunidade de pesquisa.

APÊNDICE: Fundamentos Científicos e Matemáticos

Para os interessados, aqui estão os fundamentos técnicos do nosso guia de Dinâmica de Fluidos Computacional acima. O que se segue servirá como um resumo muito útil e conciso de tópicos que normalmente são abordados ao longo de cerca de uma dúzia de cursos de pós-graduação. Estudantes de pós-graduação e tipos matemáticos interessados ​​em uma compreensão profunda do tópico podem achar este material bastante atraente.

Mecânica dos Fluidos

“Modelagem”, em geral, é o processo de resolver algum sistema real com aproximações em série. O modelo, muitas vezes, envolve equações contínuas inadequadas para implementação em computador e, portanto, deve ser aproximado com métodos numéricos.

Para a mecânica dos fluidos, vamos começar este guia pelas equações fundamentais, as equações de Navier-Stokes, e usá-las para desenvolver um esquema CFD.

As equações de Navier-Stokes são uma série de equações diferenciais parciais (EDPs) que descrevem muito bem os fluxos de fluidos e são, portanto, nosso ponto de partida. Eles podem ser derivados de leis de conservação de massa, momento e energia lançadas através de um Teorema de Transporte de Reynolds e aplicando o teorema de Gauss e invocando a Hipótese de Stoke. As equações requerem uma suposição de continuum, onde se assume que temos partículas de fluido suficientes para fornecer propriedades estatísticas, como temperatura, densidade e significado de velocidade. Além disso, é necessária uma relação linear entre o tensor de tensão superficial e o tensor de taxa de deformação, simetria no tensor de tensão e suposições de fluido isotrópico. É importante conhecer as suposições que fazemos e herdamos durante esse desenvolvimento para que possamos avaliar a aplicabilidade no código resultante. As equações de Navier-Stokes em notação de Einstein, sem mais delongas:

Conservação de massa:

Conservação da quantidade de movimento:

Conservação de energia:

onde a tensão desviatória é:

Embora muito gerais, governando a maioria dos fluxos de fluidos no mundo físico, eles não são de muita utilidade diretamente. Existem relativamente poucas soluções exatas conhecidas para as equações, e um Prêmio do Milênio de $ 1.000.000 está disponível para quem puder resolver o problema de existência e suavidade. A parte importante é que temos um ponto de partida para o desenvolvimento do nosso modelo fazendo uma série de suposições para reduzir a complexidade (são algumas das equações mais difíceis da física clássica).

Para manter as coisas “simples”, usaremos nosso conhecimento específico de domínio para fazer uma suposição incompressível sobre o fluido e assumir temperaturas constantes de modo que a equação da conservação da energia, que se torna a equação do calor, não seja necessária (desacoplada). Agora temos duas equações, ainda PDEs, mas significativamente mais simples enquanto ainda resolvemos um grande número de problemas de fluidos reais.

Equação de continuidade

Equações de momento

Neste ponto, agora temos um bom modelo matemático para fluxos de fluidos incompressíveis (gases de baixa velocidade e líquidos como água, por exemplo). Resolver essas equações diretamente à mão não é fácil, mas é bom porque podemos obter soluções “exatas” para problemas simples. Usar essas equações para resolver problemas de interesse, digamos, ar fluindo sobre uma asa ou água fluindo através de algum sistema, requer que resolvamos essas equações numericamente.

Construindo um Esquema Numérico

Para resolver problemas mais complexos usando o computador, é necessário um método para resolver numericamente nossas equações incompressíveis. Resolver equações diferenciais parciais, ou mesmo equações diferenciais, numericamente não é trivial. No entanto, nossas equações neste guia têm um desafio particular (surpresa!). Ou seja, precisamos resolver as equações de momento mantendo a divergência da solução livre, conforme exigido pela continuidade. Uma simples integração de tempo através de algo como o método Runge-Kutta é dificultada, pois a equação de continuidade não possui uma derivada de tempo dentro dela.

Não existe um método correto, ou mesmo melhor, para resolver as equações, mas existem muitas opções viáveis. Ao longo das décadas, várias abordagens foram encontradas para resolver o problema, como reformular em termos de vorticidade e função de fluxo, introduzindo compressibilidade artificial e divisão de operadores. Chorin (1969), e depois Kim e Moin (1984, 1990), formularam um método de passo fracionário muito bem-sucedido e popular que nos permitirá integrar as equações enquanto resolvemos o campo de pressão diretamente, em vez de implicitamente. O método do passo fracionário é um método geral para aproximar equações dividindo seus operadores, neste caso dividindo ao longo da pressão. A abordagem é relativamente simples e ao mesmo tempo robusta, motivando sua escolha aqui.

Primeiro, precisamos discriminar numericamente as equações no tempo para que possamos passar de um ponto no tempo para o próximo. Seguindo Kim e Moin (1984), usaremos o método de Adams-Bashforth explícito de segunda ordem para os termos convectivos, o método de Crank-Nicholson implícito de segunda ordem para os termos viscosos, uma diferença finita simples para a derivada temporal , desprezando o gradiente de pressão. Essas escolhas não são de forma alguma as únicas aproximações que podem ser feitas: sua seleção é parte da arte de construir o esquema controlando o comportamento numérico do esquema.

A velocidade intermediária agora pode ser integrada, no entanto, ignora a contribuição da pressão e agora é divergente (a incompressibilidade exige que ela seja divergente livre). O restante do operador é necessário para nos levar ao próximo passo de tempo.

Onde é algum escalar que precisamos encontrar que resulta em uma velocidade livre divergente. Podemos encontrar tomando a divergência da etapa de correção,

onde o primeiro termo é zero conforme exigido pela continuidade, produzindo uma equação de Poisson para um campo escalar que fornecerá uma velocidade solenoidal (livre divergente) no próximo passo de tempo.

Como mostram Kim e Moin (1984), não é exatamente a pressão como resultado da divisão do operador, mas pode ser encontrada por

Neste ponto do tutorial estamos indo muito bem, temos discritizado temporalmente as equações governantes para que possamos integrá-las. Agora precisamos discretizar espacialmente os operadores. Existem vários métodos com os quais podemos fazer isso, o Método dos Elementos Finitos, o Método dos Volumes Finitos e o Método das Diferenças Finitas, por exemplo. No trabalho original de Kim e Moin (1984), eles procedem com o Método das Diferenças Finitas. O método é vantajoso por sua relativa simplicidade e eficiência computacional, mas sofre para geometrias complexas, pois requer uma malha estruturada.

O Método dos Elementos Finitos (FEM) é uma seleção conveniente por sua generalidade e possui alguns projetos de código aberto muito bons auxiliando em seu uso. Em particular, ele lida com geometrias reais em uma, duas e três dimensões, dimensiona para problemas muito grandes em clusters de máquinas e é relativamente fácil de usar para elementos de alta ordem. Normalmente, o método é o mais lento dos três, no entanto, ele nos dará a maior quilometragem entre os problemas, então o usaremos aqui.

Mesmo ao implementar o FEM, existem muitas opções. Aqui usaremos o Galerkin FEM. Ao fazer isso, lançamos as equações na forma residual ponderada multiplicando cada uma por uma função de teste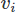 para os vetores e 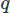para o campo escalar, e integrando sobre o domínio 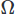. Em seguida, realizamos a integração parcial em quaisquer derivadas de alta ordem usando o teorema de Stoke ou o teorema da divergência. Em seguida, colocamos o problema variacional, produzindo nosso esquema CFD desejado.

Agora temos um bom esquema matemático em uma forma “conveniente” para implementação, esperançosamente com alguma noção do que era necessário para chegar lá (muita matemática e métodos de pesquisadores brilhantes que praticamente copiamos e ajustamos).