دليل الحوسبة العلمية بأدوات مفتوحة المصدر

تاريخيًا ، اقتصرت العلوم الحسابية إلى حد كبير على مجال علماء الأبحاث ومرشحي الدكتوراه. ومع ذلك ، على مر السنين - ربما دون علم مجتمع البرمجيات الأكبر - قمنا نحن خبراء الحوسبة العلمية بهدوء بتجميع مكتبات تعاونية مفتوحة المصدر تتعامل مع الغالبية العظمى من الرفع الثقيل . والنتيجة هي أنه أصبح الآن أسهل من أي وقت مضى تنفيذ النماذج الرياضية ، وبينما قد لا يكون المجال جاهزًا بعد للاستهلاك الشامل ، فقد تم تخفيض عائق التنفيذ الناجح بشكل كبير. يعد تطوير قاعدة بيانات حسابية جديدة من البداية مهمة ضخمة ، يتم قياسها عادةً بالسنوات ، ولكن مشاريع الحوسبة العلمية مفتوحة المصدر هذه تجعل من الممكن تشغيلها بأمثلة يمكن الوصول إليها للاستفادة بسرعة نسبيًا من هذه القدرات الحسابية.

نظرًا لأن الغرض من الحوسبة العلمية هو توفير رؤية علمية للأنظمة الحقيقية الموجودة في الطبيعة ، فإن الانضباط يمثل طليعة في جعل نهج برامج الكمبيوتر حقيقة واقعة. من أجل صنع برنامج يحاكي العالم الحقيقي بدرجة عالية جدًا من الدقة والدقة ، يجب استدعاء الرياضيات التفاضلية المعقدة ، والتي تتطلب معرفة نادرًا ما توجد خارج أسوار الجامعات أو المختبرات الوطنية أو أقسام البحث والتطوير في الشركات. علاوة على ذلك ، تظهر تحديات عددية كبيرة عند محاولة وصف النسيج المستمر والمتناهي الصغر للعالم الحقيقي باستخدام اللغة المنفصلة للأصفار والآحاد. من الضروري بذل جهد شامل للتحول العددي الدقيق لتقديم خوارزميات يمكن تتبعها حسابيًا ، والتي تقدم نتائج ذات مغزى. بمعنى آخر ، الحوسبة العلمية واجب ثقيل.

أدوات مفتوحة المصدر للحوسبة العلمية

أنا شخصياً مغرم بشكل خاص بمشروع FEniCS ، حيث استخدمه في أطروحتي ، وسأظهر تحيزي في اختيار ذلك لمثال الكود الخاص بنا لهذا البرنامج التعليمي. (هناك مشاريع أخرى عالية الجودة مثل DUNE والتي يمكن للمرء استخدامها أيضًا.)

يوصف FEniCS بأنه "مشروع تعاوني لتطوير المفاهيم والأدوات المبتكرة للحوسبة العلمية المؤتمتة ، مع التركيز بشكل خاص على الحل الآلي للمعادلات التفاضلية من خلال طرق العناصر المحدودة." هذه مكتبة قوية لحل مجموعة كبيرة من المشكلات وتطبيقات الحوسبة العلمية. من بين المساهمين فيها مختبر أبحاث Simula ، وجامعة كامبريدج ، وجامعة شيكاغو ، وجامعة بايلور ، والمعهد الملكي للتكنولوجيا KTH ، الذين قاموا بشكل جماعي ببنائه في مورد لا يقدر بثمن على مدار العقد الماضي (انظر FEniCS codewarm).

الأمر المذهل إلى حد ما هو مقدار الجهد الذي منعتنا مكتبة FEniCS منه. للتعرف على العمق المذهل واتساع نطاق الموضوعات التي يغطيها المشروع ، يمكن للمرء عرض كتابه النصي مفتوح المصدر ، حيث يقارن الفصل 21 مخططات العناصر المحدودة المختلفة لحل التدفقات غير القابلة للضغط.

وراء الكواليس ، دمج المشروع بالنسبة لنا مجموعة كبيرة من مكتبات الحوسبة العلمية مفتوحة المصدر ، والتي قد تكون ذات فائدة أو مفيدة بشكل مباشر. وتشمل هذه ، بدون ترتيب معين ، المشاريع التي يستدعيها مشروع FEniCS:

• PETSc: مجموعة من هياكل البيانات والإجراءات الروتينية للحل القابل للتطوير (المتوازي) للتطبيقات العلمية على غرار المعادلات التفاضلية الجزئية.
• مشروع Trilinos: مجموعة من الخوارزميات والتقنيات القوية لحل المعادلات الخطية وغير الخطية ، تم تطويرها من العمل في مختبرات سانديا الوطنية.
• uBLAS: "مكتبة فئة قوالب C ++ توفر وظائف BLAS من المستوى 1 و 2 و 3 للمصفوفات الكثيفة والمكتظة والمتفرقة والعديد من الخوارزميات العددية للجبر الخطي."
• GMP: مكتبة مجانية للحساب الدقيق العشوائي ، تعمل على الأعداد الصحيحة الموقعة والأرقام المنطقية وأرقام الفاصلة العائمة.
• UMFPACK: مجموعة من الإجراءات لحل الأنظمة الخطية المتفرقة غير المتماثلة ، Ax = b ، باستخدام طريقة MultiFrontal غير المتماثل.
• ParMETIS: مكتبة متوازية تعتمد على MPI تنفذ مجموعة متنوعة من الخوارزميات لتقسيم الرسوم البيانية غير المهيكلة والشبكات ولحساب أوامر تقليل التعبئة للمصفوفات المتفرقة.
• NumPy: الحزمة الأساسية للحوسبة العلمية باستخدام Python.
• CGAL: خوارزميات هندسية فعالة وموثوقة في شكل مكتبة C ++.
• SCOTCH: حزمة برامج ومكتبات لتقسيم الرسم البياني المتسلسل والمتوازي ، والتخطيط الثابت والتجميع ، وتقسيم الشبكة المتسلسلة والرسومات الفائقة ، وترتيب كتل المصفوفة المتفرقة والمتوازية.
• MPI: نظام تمرير رسائل معياري ومحمول صممه مجموعة من الباحثين من الأوساط الأكاديمية والصناعية ليعمل على مجموعة متنوعة من أجهزة الكمبيوتر المتوازية.
• VTK: نظام برمجي مفتوح المصدر ومتاح مجانًا لرسومات الكمبيوتر ثلاثية الأبعاد ومعالجة الصور والتصور.
• SLEPc: مكتبة برمجيات لحل مشاكل القيمة الذاتية المتفرقة على نطاق واسع على أجهزة الكمبيوتر المتوازية.

تمنحنا قائمة الحزم الخارجية المدمجة في المشروع إحساسًا بالإمكانيات الموروثة. على سبيل المثال ، يسمح وجود دعم متكامل لـ MPI بالتوسع عبر العاملين عن بُعد في بيئة مجموعة الحوسبة (على سبيل المثال ، سيتم تشغيل هذا الرمز على جهاز كمبيوتر فائق أو كمبيوتر محمول).

من المثير للاهتمام أيضًا ملاحظة أن هناك العديد من التطبيقات بخلاف الحوسبة العلمية التي يمكن استخدام هذه المشاريع من أجلها ، بما في ذلك النمذجة المالية ومعالجة الصور ومشكلات التحسين وربما حتى ألعاب الفيديو. سيكون من الممكن ، على سبيل المثال ، إنشاء لعبة فيديو تستخدم بعض هذه الخوارزميات والأساليب مفتوحة المصدر لحل تدفق مائع ثنائي الأبعاد ، مثل التيارات المحيطية / النهرية التي يتفاعل معها اللاعب (ربما يحاول و الإبحار بقارب عبر تدفقات متفاوتة للرياح والمياه).

تطبيق نموذجي: الاستفادة من المصدر المفتوح للحوسبة العلمية

سأحاول هنا إعطاء نكهة لما ينطوي عليه تطوير نموذج عددي من خلال إظهار كيفية تطوير مخطط ديناميكيات الموائع الحسابية الأساسي وتنفيذه في إحدى مكتبات المصادر المفتوحة هذه - في هذه الحالة مشروع FEniCS. يوفر FEnICS واجهات برمجة التطبيقات في كل من Python و C ++. في هذا المثال ، سنستخدم Python API.

سنناقش بعض المحتوى التقني إلى حد ما ، ولكن الهدف سيكون ببساطة إعطاء لمحة عما يتطلبه تطوير كود الحوسبة العلمية هذا ، ومقدار ما تفعله أدوات المصادر المفتوحة اليوم بالنسبة لنا. في هذه العملية ، نأمل أن نساعد في إزالة الغموض عن عالم الحوسبة العلمية المعقد. (لاحظ أنه يتم توفير ملحق يوضح جميع الأسس الرياضية والعلمية لأولئك الذين يهتمون بهذا المستوى من التفاصيل.)

إخلاء المسؤولية: بالنسبة لأولئك القراء الذين لديهم خلفية قليلة أو معدومة في برامج وتطبيقات الحوسبة العلمية ، قد تجعلك أجزاء من هذا المثال تشعر كما يلي:

إذا كان الأمر كذلك ، فلا تيأس. الخلاصة الرئيسية هنا هي إلى أي مدى يمكن للمشاريع مفتوحة المصدر الحالية أن تبسط إلى حد كبير العديد من هذه المهام.

مع أخذ ذلك في الاعتبار ، لنبدأ بإلقاء نظرة على العرض التوضيحي لـ FEnICS لـ Navier-Stokes غير القابلة للضغط. يقوم هذا العرض التوضيحي بنماذج ضغط وسرعة مائع غير قابل للضغط يتدفق عبر منحنى على شكل حرف L ، مثل أنبوب السباكة.

يوفر الوصف الموجود على الصفحة التجريبية المرتبطة إعدادًا ممتازًا وموجزًا ​​للخطوات الضرورية لتشغيل الكود ، وأنا أشجعك على إلقاء نظرة سريعة لمعرفة ما هو متضمن. للتلخيص ، سيحل العرض التوضيحي السرعة والضغط خلال الانحناء لمعادلات التدفق غير القابلة للضغط. يدير العرض التوضيحي محاكاة قصيرة للسائل المتدفق بمرور الوقت ، مما يؤدي إلى تحريك النتائج كما هي. يتم تحقيق ذلك عن طريق إعداد الشبكة التي تمثل الفراغ في الأنبوب ، واستخدام طريقة العناصر المحدودة لحل السرعة والضغط عدديًا عند كل نقطة على الشبكة. ثم نقوم بالتكرار عبر الزمن ، ونقوم بتحديث مجالات السرعة والضغط أثناء تقدمنا ​​، مرة أخرى باستخدام المعادلات التي لدينا تحت تصرفنا.

يعمل العرض التوضيحي كما هو ، لكننا سنقوم بتعديله بشكل طفيف. يستخدم العرض التوضيحي تقسيم Chorin ، لكننا سنستخدم طريقة مختلفة قليلاً مستوحاة من Kim و Moin بدلاً من ذلك ، والتي نأمل أن تكون أكثر استقرارًا. يتطلب هذا منا فقط تغيير المعادلة المستخدمة لتقريب المصطلحات الحملية واللزجة ، ولكن للقيام بذلك نحتاج إلى تخزين حقل السرعة للخطوة الزمنية السابقة ، وإضافة مصطلحين إضافيين إلى معادلة التحديث ، والتي ستستخدم ذلك السابق معلومات لتقريب رقمي أكثر دقة.

لذلك دعونا نجري هذا التغيير. أولاً ، نضيف كائن Function جديدًا إلى الإعداد. هذا كائن يمثل دالة رياضية مجردة مثل حقل متجه أو قياسي. un1 وسوف تخزن حقل السرعة السابق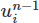 على مساحة V

 ... # Create functions (three distinct vector fields and a scalar field) un1 = Function(V) # the previous time step's velocity field we are adding u0 = Function(V) # the current velocity field u1 = Function(V) # the next velocity field (what's being solved for) p1 = Function(Q) # the next pressure field (what's being solved for) ...

بعد ذلك ، نحتاج إلى تغيير الطريقة التي يتم بها تحديث "السرعة المؤقتة" خلال كل خطوة من خطوات المحاكاة. يمثل هذا الحقل السرعة التقريبية في الخطوة الزمنية التالية عندما يتم تجاهل الضغط (عند هذه النقطة لم يكن الضغط معروفًا بعد). هذا هو المكان الذي نستبدل فيه طريقة تقسيم كورين بطريقة الخطوة الكسرية الأكثر حداثة من Kim و Moin. بمعنى آخر ، سنقوم بتغيير تعبير الحقل F1 :

يستبدل:

 # Tentative velocity field (a first prediction of what the next velocity field is) # for the Chorin style split # F1 = change in the velocity field + # convective term + # diffusive term - # body force term F1 = (1/k)*inner(u - u0, v)*dx + \ inner(grad(u0)*u0, v)*dx + \ nu*inner(grad(u), grad(v))*dx - \ inner(f, v)*dx

مع:

 # Tentative velocity field (a first prediction of what the next velocity field is) # for the Kim and Moin style split # F1 = change in the velocity field + # convective term + # diffusive term - # body force term F1 = (1/k)*inner(u - u0, v)*dx + \ (3.0/2.0) * inner(grad(u0)*u0, v)*dx - (1.0/2.0) * inner(grad(un1)*un1, v)*dx + \ (nu/2.0)*inner(grad(u+u0), grad(v))*dx - \ inner(f, v)*dx

بحيث يستخدم العرض التوضيحي الآن طريقتنا المحدثة لحل مجال السرعة المتوسطة عند استخدام F1 .

أخيرًا ، تأكد من أننا نقوم بتحديث حقل السرعة السابق ، un1 ، في نهاية كل خطوة من خطوات التكرار

 ... # Move to next time step un1.assign(u0) # copy the current velocity field into the previous velocity field u0.assign(u1) # copy the next velocity field into the current velocity field ...

بحيث يكون ما يلي هو الكود الكامل من العرض التوضيحي لـ FEniCS CFD ، مع تضمين تغييراتنا:

 """This demo program solves the incompressible Navier-Stokes equations on an L-shaped domain using Kim and Moin's fractional step method.""" # Begin demo from dolfin import * # Print log messages only from the root process in parallel parameters["std_out_all_processes"] = False; # Load mesh from file mesh = Mesh("lshape.xml.gz") # Define function spaces (P2-P1) V = VectorFunctionSpace(mesh, "Lagrange", 2) Q = FunctionSpace(mesh, "Lagrange", 1) # Define trial and test functions u = TrialFunction(V) p = TrialFunction(Q) v = TestFunction(V) q = TestFunction(Q) # Set parameter values dt = 0.01 T = 3 nu = 0.01 # Define time-dependent pressure boundary condition p_in = Expression("sin(3.0*t)", t=0.0) # Define boundary conditions noslip = DirichletBC(V, (0, 0), "on_boundary && \ (x[0] < DOLFIN_EPS | x[1] < DOLFIN_EPS | \ (x[0] > 0.5 - DOLFIN_EPS && x[1] > 0.5 - DOLFIN_EPS))") inflow = DirichletBC(Q, p_in, "x[1] > 1.0 - DOLFIN_EPS") outflow = DirichletBC(Q, 0, "x[0] > 1.0 - DOLFIN_EPS") bcu = [noslip] bcp = [inflow, outflow] # Create functions un1 = Function(V) u0 = Function(V) u1 = Function(V) p1 = Function(Q) # Define coefficients k = Constant(dt) f = Constant((0, 0)) # Tentative velocity field (a first prediction of what the next velocity field is) # for the Kim and Moin style split # F1 = change in the velocity field + # convective term + # diffusive term - # body force term F1 = (1/k)*inner(u - u0, v)*dx + \ (3.0/2.0) * inner(grad(u0)*u0, v)*dx - (1.0/2.0) * inner(grad(un1)*un1, v)*dx + \ (nu/2.0)*inner(grad(u+u0), grad(v))*dx - \ inner(f, v)*dx a1 = lhs(F1) L1 = rhs(F1) # Pressure update a2 = inner(grad(p), grad(q))*dx L2 = -(1/k)*div(u1)*q*dx # Velocity update a3 = inner(u, v)*dx L3 = inner(u1, v)*dx - k*inner(grad(p1), v)*dx # Assemble matrices A1 = assemble(a1) A2 = assemble(a2) A3 = assemble(a3) # Use amg preconditioner if available prec = "amg" if has_krylov_solver_preconditioner("amg") else "default" # Create files for storing solution ufile = File("results/velocity.pvd") pfile = File("results/pressure.pvd") # Time-stepping t = dt while t < T + DOLFIN_EPS: # Update pressure boundary condition p_in.t = t # Compute tentative velocity step begin("Computing tentative velocity") b1 = assemble(L1) [bc.apply(A1, b1) for bc in bcu] solve(A1, u1.vector(), b1, "gmres", "default") end() # Pressure correction begin("Computing pressure correction") b2 = assemble(L2) [bc.apply(A2, b2) for bc in bcp] solve(A2, p1.vector(), b2, "cg", prec) end() # Velocity correction begin("Computing velocity correction") b3 = assemble(L3) [bc.apply(A3, b3) for bc in bcu] solve(A3, u1.vector(), b3, "gmres", "default") end() # Plot solution plot(p1, title="Pressure", rescale=True) plot(u1, title="Velocity", rescale=True) # Save to file ufile << u1 pfile << p1 # Move to next time step un1.assign(u0) u0.assign(u1) t += dt print "t =", t # Hold plot interactive()

تشغيل البرنامج يظهر التدفق حول الكوع. قم بتشغيل كود الحوسبة العلمية بنفسك لترى أنه يتحرك! يتم عرض شاشات الإطار النهائي أدناه.

الضغوط النسبية في المنعطف في نهاية المحاكاة ، مع تحجيمها وتلوينها من حيث الحجم (القيم غير الأبعاد):

السرعات النسبية في المنعطف في نهاية المحاكاة حيث يتم قياس الحروف الرسومية المتجهة وتلوينها حسب الحجم (القيم غير الأبعاد).

لذا فإن ما فعلناه هو أخذ عرض توضيحي موجود ، والذي يحدث لتنفيذ مخطط مشابه جدًا لنظامنا بسهولة إلى حد ما ، وتعديله لاستخدام تقديرات تقريبية أفضل باستخدام المعلومات من الخطوة الزمنية السابقة.

في هذه المرحلة ، قد تعتقد أن هذا كان تعديلاً تافهاً. كان الأمر كذلك ، وهذه هي النقطة إلى حد كبير. سمح لنا مشروع الحوسبة العلمية مفتوح المصدر هذا بتنفيذ نموذج رقمي معدل بسرعة عن طريق تغيير أربعة أسطر من التعليمات البرمجية. قد تستغرق هذه التغييرات شهورًا في رموز البحث الكبيرة.

يحتوي المشروع على العديد من العروض التوضيحية الأخرى التي يمكن استخدامها كنقطة انطلاق. حتى أن هناك عددًا من التطبيقات مفتوحة المصدر مبنية على المشروع والتي تنفذ نماذج مختلفة.

خاتمة

الحوسبة العلمية وتطبيقاتها معقدة بالفعل. لا يوجد التفاف على ذلك. ولكن كما هو الحال بشكل متزايد في العديد من المجالات ، فإن المشهد المتزايد باستمرار للأدوات والمشاريع مفتوحة المصدر المتاحة يمكن أن يبسط بشكل كبير ما يمكن أن يكون مهام برمجة معقدة للغاية ومملة. وربما يكون الوقت قريبًا من حيث تصبح الحوسبة العلمية متاحة بما يكفي لتجد نفسها تُستخدم بسهولة خارج مجتمع البحث.

الملحق: الأسس العلمية والرياضية

للمهتمين ، إليك الأسس التقنية لدليل ديناميكيات الموائع الحسابية أعلاه. ما يلي سيكون بمثابة ملخص مفيد وموجز للغاية للموضوعات التي يتم تناولها عادةً على مدار اثنتي عشرة دورة أو نحو ذلك على مستوى الدراسات العليا. قد يجد طلاب الدراسات العليا والأنواع الرياضية المهتمة بالفهم العميق للموضوع هذه المادة جذابة للغاية.

ميكانيكا الموائع

"النمذجة" ، بشكل عام ، هي عملية حل نظام حقيقي بتقريب متسلسل. غالبًا ما يشتمل النموذج على معادلات مستمرة غير مناسبة لتطبيق الكمبيوتر ، وبالتالي يجب تقريبه بشكل أكبر باستخدام الطرق العددية.

بالنسبة لميكانيكا الموائع ، لنبدأ هذا الدليل من المعادلات الأساسية ، معادلات نافيير-ستوكس ، ونستخدمها لتطوير مخطط CFD.

معادلات نافيير-ستوكس عبارة عن سلسلة من المعادلات التفاضلية الجزئية (PDEs) التي تصف تدفقات السوائل بشكل جيد جدًا وبالتالي فهي نقطة البداية. يمكن اشتقاقها من قوانين الكتلة والزخم والحفاظ على الطاقة التي تم طرحها من خلال نظرية رينولدز للنقل وتطبيق نظرية غاوس واستدعاء فرضية ستوك. تتطلب المعادلات افتراضًا متصلًا ، حيث يُفترض أن لدينا جزيئات سائلة كافية لإعطاء خصائص إحصائية مثل معنى درجة الحرارة والكثافة والسرعة. بالإضافة إلى ذلك ، هناك حاجة إلى علاقة خطية بين موتر الإجهاد السطحي وموتّر معدل الإجهاد ، والتماثل في موتر الإجهاد ، وافتراضات الموائع المتناحرة. من المهم معرفة الافتراضات التي نصنعها ونرثها خلال هذا التطوير حتى نتمكن من تقييم قابلية التطبيق في الكود الناتج. معادلات نافيير-ستوكس في تدوين أينشتاين ، دون مزيد من اللغط:

حفظ الكتلة:

الحفاظ على الزخم:

الحفاظ على الطاقة:

حيث يكون الضغط الانحرافى:

على الرغم من كونها عامة جدًا ، وتحكم معظم تدفقات السوائل في العالم المادي ، إلا أنها ليست ذات فائدة كبيرة بشكل مباشر. هناك عدد قليل نسبيًا من الحلول الدقيقة المعروفة للمعادلات ، وجائزة الألفية 1،000،000 دولار متاحة لأي شخص يمكنه حل مشكلة الوجود والنعومة. الجزء المهم هو أن لدينا نقطة انطلاق لتطوير نموذجنا من خلال وضع سلسلة من الافتراضات لتقليل التعقيد (فهي من أصعب المعادلات في الفيزياء الكلاسيكية).

لإبقاء الأمور "بسيطة" ، سنستخدم معرفتنا الخاصة بالمجال لعمل افتراض غير قابل للضغط على السائل ، ونفترض درجات حرارة ثابتة بحيث لا تكون هناك حاجة إلى حفظ معادلة الطاقة ، التي تصبح معادلة الحرارة (منفصلة). لدينا الآن معادلتان ، ما زالتا PDEs ، لكنهما أبسط بشكل ملحوظ مع حل عدد كبير من مشاكل السوائل الحقيقية.

معادلة الاستمرارية

معادلات الزخم

في هذه المرحلة ، لدينا الآن نموذج رياضي رائع لتدفقات السوائل غير القابلة للضغط (الغازات والسوائل منخفضة السرعة مثل الماء ، على سبيل المثال). إن حل هذه المعادلات يدويًا ليس بالأمر السهل ، لكن من الجيد أنه يمكننا الحصول على حلول "دقيقة" للمسائل البسيطة. يتطلب استخدام هذه المعادلات لمعالجة المشكلات ذات الأهمية ، مثل تدفق الهواء فوق الجناح ، أو تدفق الماء عبر بعض الأنظمة ، أن نحل هذه المعادلات عدديًا.

بناء نظام عددي

لحل المشاكل الأكثر تعقيدًا باستخدام الكمبيوتر ، هناك حاجة إلى طريقة لحل المعادلات غير القابلة للضغط عدديًا. حل المعادلات التفاضلية الجزئية ، أو حتى المعادلات التفاضلية ، ليس بالأمر السهل. ومع ذلك ، فإن معادلاتنا في هذا الدليل لها تحدي خاص (مفاجأة!). أي أننا بحاجة إلى حل معادلات الزخم مع الحفاظ على تباعد الحل خاليًا ، كما هو مطلوب من خلال الاستمرارية. أصبح تكامل الوقت البسيط من خلال شيء مثل طريقة Runge-Kutta أمرًا صعبًا نظرًا لأن معادلة الاستمرارية لا تحتوي على مشتق زمني بداخلها.

لا توجد طريقة صحيحة ، أو حتى أفضل ، لحل المعادلات ، ولكن هناك العديد من الخيارات العملية. على مدى عقود ، تم العثور على العديد من الأساليب لمعالجة المشكلة ، مثل إعادة الصياغة من حيث الدوامة ووظيفة التدفق ، وإدخال الانضغاط الاصطناعي ، وتقسيم المشغل. كورين (1969) ، ثم كيم وموين (1984 ، 1990) ، صاغا طريقة خطوة كسرية ناجحة جدًا وشائعة والتي ستسمح لنا بدمج المعادلات أثناء حل مجال الضغط بشكل مباشر ، وليس ضمنيًا. طريقة الخطوة الكسرية هي طريقة عامة لتقريب المعادلات عن طريق تقسيم مشغليها ، في هذه الحالة الانقسام على طول الضغط. النهج بسيط نسبيًا ولكنه قوي ، مما يحفز اختياره هنا.

أولًا ، نحتاج إلى تمييز المعادلات رقميًا في الوقت المناسب حتى نتمكن من الانتقال من نقطة زمنية إلى أخرى. في اتباع Kim and Moin (1984) ، سوف نستخدم طريقة Adams-Bashforth من الدرجة الثانية الصريحة للمصطلحات الحملية ، طريقة Crank-Nicholson من الدرجة الثانية الضمنية للمصطلحات اللزجة ، وهو فرق محدود بسيط لمشتق الوقت ، مع إهمال تدرج الضغط. هذه الاختيارات ليست بأي حال من الأحوال التقريبات الوحيدة التي يمكن إجراؤها: اختيارهم هو جزء من الفن في بناء المخطط من خلال التحكم في السلوك العددي للمخطط.

يمكن الآن دمج السرعة المتوسطة ، ومع ذلك ، فإنها تتجاهل مساهمة الضغط وهي الآن متباعدة (تتطلب عدم الانضغاط أن تكون خالية من التباعد). نحتاج إلى ما تبقى من عامل التشغيل لنقلنا إلى الخطوة التالية.

أين هو نوع من العددي نحتاج إلى إيجاد أيهما يؤدي إلى سرعة حرة متباينة. نحن نستطيع ان نجد من خلال اتخاذ خطوة تصحيح الاختلاف ،

حيث يكون المصطلح الأول صفرًا كما هو مطلوب من خلال الاستمرارية ، مما ينتج عنه معادلة بواسون لحقل قياسي والذي سيوفر سرعة ملف لولبي (خالٍ من التباعد) في الخطوة الزمنية التالية.

كما أظهر Kim and Moin (1984) ، ليس بالضبط الضغط الناتج عن انقسام المشغل ، ولكن يمكن العثور عليه بواسطة

في هذه المرحلة من البرنامج التعليمي ، نقوم بعمل جيد إلى حد ما ، لقد قمنا مؤقتًا بتقسيم المعادلات الحاكمة حتى نتمكن من دمجها. نحن الآن بحاجة إلى تمييز المشغلين مكانيًا. يوجد عدد من الطرق التي يمكننا من خلالها تحقيق ذلك ، مثل طريقة العناصر المحدودة وطريقة الحجم المحدود وطريقة الفروق المحدودة ، على سبيل المثال. في العمل الأصلي لكيم وموين (1984) ، شرعوا في طريقة الفروق المحدودة. تعتبر هذه الطريقة مفيدة لبساطتها النسبية وكفاءتها الحسابية ، ولكنها تعاني من الأشكال الهندسية المعقدة لأنها تتطلب شبكة منظمة.

تعتبر طريقة العناصر المحدودة (FEM) اختيارًا مناسبًا لعموميتها ولديها بعض المشاريع مفتوحة المصدر اللطيفة جدًا التي تساعد في استخدامها. على وجه الخصوص ، يتعامل مع الأشكال الهندسية الحقيقية بأبعاد واحدة وثنائية وثلاثية ، ومقاييس للمشكلات الكبيرة جدًا في مجموعات الماكينة ، وهو سهل الاستخدام نسبيًا لعناصر الترتيب العالي. عادةً ما تكون الطريقة أبطأ من الثلاثة ، ولكنها ستمنحنا أكبر عدد من الأميال عبر المشاكل ، لذلك سنستخدمها هنا.

حتى عند تنفيذ FEM ، هناك العديد من الخيارات. هنا سوف نستخدم Galerkin FEM. عند القيام بذلك ، قمنا بطرح المعادلات في صورة متبقية موزونة بضرب كل منها في دالة اختبار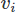 لناقلات و 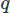للحقل القياسي ، والتكامل عبر المجال 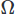. نقوم بعد ذلك بإجراء تكامل جزئي على أي مشتقات عالية الرتبة باستخدام نظرية ستوك أو نظرية الاختلاف. ثم نطرح مشكلة التباين ، ونحصل على مخطط CFD المطلوب.

لدينا الآن مخطط رياضي جميل في شكل "مناسب" للتنفيذ ، ونأمل أن يكون مع بعض الإحساس بما هو مطلوب للوصول إلى هناك (الكثير من الرياضيات ، وطرق من باحثين لامعين نقوم بنسخها وتعديلها إلى حد كبير).