オープンソースツールを使用した科学計算ガイド

歴史的に、計算科学は主に研究科学者と博士課程の候補者の領域に限定されてきました。 しかし、何年にもわたって、おそらく大規模なソフトウェアコミュニティには知られていないが、私たちの科学計算エッグヘッズは、大部分の重労働を処理する共同オープンソースライブラリを静かにコンパイルしてきました。 その結果、数学モデルの実装がこれまでになく簡単になり、フィールドはまだ大量消費の準備ができていない可能性がありますが、実装を成功させるための基準は大幅に低くなっています。 新しい計算コードベースをゼロから開発することは、通常は数年で測定される大規模な作業ですが、これらのオープンソースの科学計算プロジェクトは、アクセス可能な例を使用して実行し、これらの計算能力を比較的迅速に活用することを可能にします。

科学計算の目的は、自然界に存在する実際のシステムへの科学的洞察を提供することであるため、この分野は、コンピューターソフトウェアを現実に近づけるための最先端を表しています。 実世界を非常に高い精度と解像度で模倣するソフトウェアを作成するには、複雑な微分数学を呼び出す必要があり、大学、国立研究所、または企業の研究開発部門の壁を越えてめったに見られない知識が必要です。 これに加えて、0と1の離散言語を使用して実世界の連続的で微小な構造を記述しようとすると、重要な数値上の課題が発生します。 計算上扱いやすく、意味のある結果をレンダリングするアルゴリズムをレンダリングするには、慎重な数値変換の徹底的な努力が必要です。 言い換えれば、科学計算は重い義務です。

科学計算のためのオープンソースツール

私は個人的にFEniCSプロジェクトが特に好きで、それを論文の仕事に使用しています。このチュートリアルのコード例では、FEniCSプロジェクトを選択する際のバイアスを示します。 （DUNEのような他の非常に高品質のプロジェクトも使用できます。）

FEniCSは、「有限要素法による微分方程式の自動解法に特に焦点を当てた、自動化された科学計算のための革新的な概念とツールの開発のための共同プロジェクト」と自称しています。 これは、膨大な数の問題や科学計算アプリケーションを解決するための強力なライブラリです。 その貢献者には、Simula Research Laboratory、ケンブリッジ大学、シカゴ大学、ベイラー大学、およびKTH Royal Institute of Technologyが含まれ、過去10年間で貴重なリソースにまとめて組み込まれています（FEniCSコードウォームを参照）。

かなり驚くべきことは、FEniCSライブラリが私たちをどれだけの努力から守ってきたかということです。 プロジェクトがカバーするトピックの驚くべき深さと幅を理解するために、オープンソースの教科書を見ることができます。第21章では、非圧縮性流れを解くためのさまざまな有限要素スキームを比較しています。

舞台裏では、プロジェクトは私たちのためにオープンソースの科学計算ライブラリの大規模なセットを統合しました。これらは興味があるか、直接使用される可能性があります。 これらには、順不同で、FEniCSプロジェクトが呼び出すプロジェクトが含まれます。

• PETSc：偏微分方程式によってモデル化された科学アプリケーションのスケーラブルな（並列）ソリューションのための一連のデータ構造とルーチン。
• Trilinosプロジェクト：Sandia National Labsでの作業から開発された、線形方程式と非線形方程式の両方を解くための一連の堅牢なアルゴリズムとテクノロジー。
• uBLAS：「高密度、パック、スパース行列用のBLASレベル1、2、3機能、および線形代数用の多くの数値アルゴリズムを提供するC++テンプレートクラスライブラリ。」
• GMP：符号付き整数、有理数、および浮動小数点数を操作する、任意精度の算術演算用の無料ライブラリ。
• UMFPACK：非対称MultiFrontal法を使用して、非対称スパース線形システムAx=bを解くための一連のルーチン。
• ParMETIS：非構造化グラフ、メッシュを分割し、スパース行列の塗りつぶしを減らす順序を計算するためのさまざまなアルゴリズムを実装するMPIベースの並列ライブラリ。
• NumPy：Pythonを使用した科学計算の基本パッケージ。
• CGAL：C++ライブラリ形式の効率的で信頼性の高い幾何学的アルゴリズム。
• SCOTCH：シーケンシャルおよびパラレルグラフパーティショニング、静的マッピングとクラスタリング、シーケンシャルメッシュとハイパーグラフパーティショニング、シーケンシャルおよびパラレルスパース行列ブロックの順序付けのためのソフトウェアパッケージとライブラリ。
• MPI：さまざまな並列コンピューターで機能するように、学界および産業界の研究者グループによって設計された、標準化されたポータブルなメッセージパッシングシステム。
• VTK：3Dコンピュータグラフィックス、画像処理、視覚化のためのオープンソースの無料で利用できるソフトウェアシステム。
• SLEPc：並列コンピューターでの大規模なスパース固有値問題を解決するためのソフトウェアライブラリ。

プロジェクトに統合されたこの外部パッケージのリストは、継承された機能の感覚を私たちに与えます。 たとえば、MPIのサポートを統合すると、コンピューティングクラスター環境のリモートワーカー間でのスケーリングが可能になります（つまり、このコードはスーパーコンピューターまたはラップトップで実行されます）。

また、財務モデリング、画像処理、最適化問題、さらにはビデオゲームなど、これらのプロジェクトを利用できる科学計算以外の多くのアプリケーションがあることに注意することも興味深いです。 たとえば、これらのオープンソースアルゴリズムと手法のいくつかを使用して、プレーヤーが対話する海/川の流れなどの2次元の流体の流れを解決するビデオゲームを作成することができます（おそらく、さまざまな風と水の流れでボートを横切って航行します）。

サンプルアプリケーション：科学計算のためのオープンソースの活用

ここでは、基本的な計算流体力学スキームがこれらのオープンソースライブラリの1つ（この場合はFEniCSプロジェクト）でどのように開発および実装されているかを示すことにより、数値モデルの開発に含まれるもののフレーバーを示します。 FEnICSは、PythonとC++の両方でAPIを提供します。 この例では、PythonAPIを使用します。

かなり技術的な内容について説明しますが、目標は、そのような科学計算コードの開発に伴うものと、今日のオープンソースツールが私たちにどれだけの手間をかけるかを味わうことです。 その過程で、科学計算の複雑な世界をわかりやすく説明できるようになることを願っています。 （その詳細レベルに関心のある人のために、すべての数学的および科学的基盤を詳述する付録が提供されていることに注意してください。）

免責事項：科学計算ソフトウェアおよびアプリケーションのバックグラウンドがほとんどまたはまったくない読者の場合、この例の一部で次のように感じることがあります。

もしそうなら、絶望しないでください。 ここでの主なポイントは、既存のオープンソースプロジェクトがこれらのタスクの多くを大幅に簡素化できる範囲です。

それを念頭に置いて、非圧縮性ナビエ・ストークスのFEnICSデモを見てみましょう。 このデモでは、配管パイプなど、L字型のベンドを流れる非圧縮性流体の圧力と速度をモデル化します。

リンクされたデモページの説明は、コードを実行するために必要な手順の優れた簡潔なセットアップを提供します。何が関係しているかを簡単に確認することをお勧めします。 要約すると、デモでは、非圧縮性流れ方程式のベンドを通る速度と圧力を解きます。 デモでは、時間の経過とともに流れる流体の短いシミュレーションを実行し、結果をアニメーション化します。 これは、パイプ内の空間を表すメッシュを設定し、有限要素法を使用してメッシュ上の各ポイントでの速度と圧力を数値的に解くことによって実現されます。 次に、時間をかけて反復し、速度と圧力のフィールドを更新しながら、自由に使用できる方程式を使用します。

デモはそのままでうまく機能しますが、少し変更します。 デモではChorinスプリットを使用しますが、代わりにKimとMoinに触発されたわずかに異なる方法を使用します。これは、より安定していることを願っています。 これには、対流項と粘性項の近似に使用される方程式を変更する必要がありますが、そのためには、前のタイムステップの速度フィールドを保存し、更新方程式に2つの項を追加する必要があります。これにより、前の項が使用されます。より正確な数値近似のための情報。

それでは、この変更を加えましょう。 まず、セットアップに新しいFunctionオブジェクトを追加します。 これは、ベクトルやスカラー場などの抽象的な数学関数を表すオブジェクトです。 これをun1と呼び、前の速度フィールドを保存します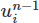関数空間Vで。

 ... # Create functions (three distinct vector fields and a scalar field) un1 = Function(V) # the previous time step's velocity field we are adding u0 = Function(V) # the current velocity field u1 = Function(V) # the next velocity field (what's being solved for) p1 = Function(Q) # the next pressure field (what's being solved for) ...

次に、シミュレーションの各ステップで「暫定速度」を更新する方法を変更する必要があります。 このフィールドは、圧力が無視されたときの次のタイムステップでの概算速度を表します（この時点では、圧力はまだ不明です）。 ここで、Chorin分割法を、より最近のKimandMoin分数ステップ法に置き換えます。 つまり、フィールドF1の式を変更します。

交換：

 # Tentative velocity field (a first prediction of what the next velocity field is) # for the Chorin style split # F1 = change in the velocity field + # convective term + # diffusive term - # body force term F1 = (1/k)*inner(u - u0, v)*dx + \ inner(grad(u0)*u0, v)*dx + \ nu*inner(grad(u), grad(v))*dx - \ inner(f, v)*dx

と：

 # Tentative velocity field (a first prediction of what the next velocity field is) # for the Kim and Moin style split # F1 = change in the velocity field + # convective term + # diffusive term - # body force term F1 = (1/k)*inner(u - u0, v)*dx + \ (3.0/2.0) * inner(grad(u0)*u0, v)*dx - (1.0/2.0) * inner(grad(un1)*un1, v)*dx + \ (nu/2.0)*inner(grad(u+u0), grad(v))*dx - \ inner(f, v)*dx

そのため、デモでは、 F1を使用するときに、中間速度フィールドを解くための更新された方法を使用します。

最後に、各反復ステップの最後に、前の速度フィールドun1を更新していることを確認します。

 ... # Move to next time step un1.assign(u0) # copy the current velocity field into the previous velocity field u0.assign(u1) # copy the next velocity field into the current velocity field ...

以下は、FEniCS CFDデモからの完全なコードであり、変更が含まれています。

 """This demo program solves the incompressible Navier-Stokes equations on an L-shaped domain using Kim and Moin's fractional step method.""" # Begin demo from dolfin import * # Print log messages only from the root process in parallel parameters["std_out_all_processes"] = False; # Load mesh from file mesh = Mesh("lshape.xml.gz") # Define function spaces (P2-P1) V = VectorFunctionSpace(mesh, "Lagrange", 2) Q = FunctionSpace(mesh, "Lagrange", 1) # Define trial and test functions u = TrialFunction(V) p = TrialFunction(Q) v = TestFunction(V) q = TestFunction(Q) # Set parameter values dt = 0.01 T = 3 nu = 0.01 # Define time-dependent pressure boundary condition p_in = Expression("sin(3.0*t)", t=0.0) # Define boundary conditions noslip = DirichletBC(V, (0, 0), "on_boundary && \ (x[0] < DOLFIN_EPS | x[1] < DOLFIN_EPS | \ (x[0] > 0.5 - DOLFIN_EPS && x[1] > 0.5 - DOLFIN_EPS))") inflow = DirichletBC(Q, p_in, "x[1] > 1.0 - DOLFIN_EPS") outflow = DirichletBC(Q, 0, "x[0] > 1.0 - DOLFIN_EPS") bcu = [noslip] bcp = [inflow, outflow] # Create functions un1 = Function(V) u0 = Function(V) u1 = Function(V) p1 = Function(Q) # Define coefficients k = Constant(dt) f = Constant((0, 0)) # Tentative velocity field (a first prediction of what the next velocity field is) # for the Kim and Moin style split # F1 = change in the velocity field + # convective term + # diffusive term - # body force term F1 = (1/k)*inner(u - u0, v)*dx + \ (3.0/2.0) * inner(grad(u0)*u0, v)*dx - (1.0/2.0) * inner(grad(un1)*un1, v)*dx + \ (nu/2.0)*inner(grad(u+u0), grad(v))*dx - \ inner(f, v)*dx a1 = lhs(F1) L1 = rhs(F1) # Pressure update a2 = inner(grad(p), grad(q))*dx L2 = -(1/k)*div(u1)*q*dx # Velocity update a3 = inner(u, v)*dx L3 = inner(u1, v)*dx - k*inner(grad(p1), v)*dx # Assemble matrices A1 = assemble(a1) A2 = assemble(a2) A3 = assemble(a3) # Use amg preconditioner if available prec = "amg" if has_krylov_solver_preconditioner("amg") else "default" # Create files for storing solution ufile = File("results/velocity.pvd") pfile = File("results/pressure.pvd") # Time-stepping t = dt while t < T + DOLFIN_EPS: # Update pressure boundary condition p_in.t = t # Compute tentative velocity step begin("Computing tentative velocity") b1 = assemble(L1) [bc.apply(A1, b1) for bc in bcu] solve(A1, u1.vector(), b1, "gmres", "default") end() # Pressure correction begin("Computing pressure correction") b2 = assemble(L2) [bc.apply(A2, b2) for bc in bcp] solve(A2, p1.vector(), b2, "cg", prec) end() # Velocity correction begin("Computing velocity correction") b3 = assemble(L3) [bc.apply(A3, b3) for bc in bcu] solve(A3, u1.vector(), b3, "gmres", "default") end() # Plot solution plot(p1, title="Pressure", rescale=True) plot(u1, title="Velocity", rescale=True) # Save to file ufile << u1 pfile << p1 # Move to next time step un1.assign(u0) u0.assign(u1) t += dt print "t =", t # Hold plot interactive()

プログラムを実行すると、肘の周りの流れが表示されます。 科学計算コードを自分で実行して、アニメーションを確認してください。 最終フレームの画面を以下に示します。

シミュレーション終了時のベンド内の相対圧力。大きさ（無次元値）によってスケーリングおよび色付けされています。

大きさ（無次元値）によってスケーリングおよび色付けされたベクトルグリフとしての、シミュレーション終了時のベンドの相対速度。

したがって、私たちが行ったことは、既存のデモを採用したものです。これは、私たちのスキームと非常によく似たスキームをかなり簡単に実装し、前のタイムステップの情報を使用してより適切な近似を使用するように変更しました。

この時点で、それは些細な編集だと思っているかもしれません。 それはそうでした、そしてそれは主にポイントです。 このオープンソースの科学計算プロジェクトにより、4行のコードを変更することで、修正された数値モデルをすばやく実装できました。 このような変更は、大規模な研究コードでは数か月かかる場合があります。

プロジェクトには、出発点として使用できる他の多くのデモがあります。 プロジェクト上に構築され、さまざまなモデルを実装するオープンソースアプリケーションも数多くあります。

結論

科学計算とその応用は確かに複雑です。 それを回避することはできません。 しかし、非常に多くのドメインでますます真実になっているように、利用可能なオープンソースツールとプロジェクトの成長し続ける風景は、そうでなければ非常に複雑で退屈なプログラミングタスクを大幅に簡素化できます。 そしておそらく、科学計算が研究コミュニティを超えて容易に利用されるのに十分なほどアクセス可能になる時期が近づいています。

付録：科学的および数学的基盤

興味のある方のために、上記の計算流体力学ガイドの技術的基盤を以下に示します。 以下は、通常、12かそこらの大学院レベルのコースでカバーされるトピックの非常に有用で簡潔な要約として役立ちます。 トピックの深い理解に興味のある大学院生や数学のタイプは、この資料が非常に魅力的であると感じるかもしれません。

流体力学

「モデリング」は、一般に、一連の近似を使用して実際のシステムを解くプロセスです。 このモデルには、コンピューターの実装に適さない連続方程式が含まれることが多いため、数値的手法でさらに近似する必要があります。

流体力学については、基本方程式であるナビエ-ストークス方程式からこのガイドを開始し、それを使用してCFDスキームを開発しましょう。

ナビエ・ストークス方程式は一連の偏微分方程式（PDE）であり、流体の流れを非常によく記述しているため、出発点になります。 それらは、レイノルズの輸送定理を介してスローされ、ガウスの定理を適用し、ストークの仮説を呼び出す質量、運動量、およびエネルギー保存の法則から導き出すことができます。 方程式には連続体の仮定が必要です。ここでは、温度、密度、速度の意味などの統計的特性を与えるのに十分な流体粒子があると仮定しています。 さらに、表面応力テンソルとひずみ速度テンソルの間の線形関係、応力テンソルの対称性、および等方性流体の仮定が必要です。 結果のコードでの適用性を評価できるように、この開発中に作成および継承する仮定を知ることが重要です。 アインシュタインの縮約記のナビエ・ストークス方程式。

質量保存：

勢いの保存：

電気の保存：

ここで、偏差応力は次のとおりです。

非常に一般的ですが、物理的な世界のほとんどの流体の流れを支配しますが、それらは直接あまり役に立ちません。 方程式の正確な解は比較的少なく、存在と滑らかさの問題を解決できる人には、1,000,000ドルのミレニアム賞が贈られます。 重要な部分は、複雑さを軽減するために一連の仮定を行うことによってモデルを開発するための出発点があることです（これらは古典物理学で最も難しい方程式のいくつかです）。

物事を「単純」に保つために、ドメイン固有の知識を使用して流体の非圧縮性の仮定を行い、熱方程式となるエネルギー方程式の保存が不要（分離）になるように一定の温度を仮定します。 これで2つの方程式ができましたが、それでもPDEですが、実際の流体の問題を多数解決しながら、大幅に単純化されています。

連続の方程式

運動量方程式

この時点で、非圧縮性流体の流れ（たとえば、低速の気体や水などの液体）の優れた数学モデルができました。 これらの方程式を手作業で直接解くことは簡単ではありませんが、単純な問題の「正確な」解を得ることができるという点で優れています。 これらの方程式を使用して、翼の上を流れる空気やシステムを流れる水など、関心のある問題に対処するには、これらの方程式を数値的に解く必要があります。

数値スキームの構築

コンピュータを使用してより複雑な問題を解決するには、非圧縮性方程式を数値的に解く方法が必要です。 偏微分方程式、あるいは微分方程式を数値的に解くことは簡単ではありません。 ただし、このガイドの方程式には特定の課題があります（驚きです！）。 つまり、連続性で必要とされるように、解の発散をなくしながら運動量方程式を解く必要があります。 ルンゲクッタ法のような単純な時間積分は、連続の方程式に時間微分が含まれていないため、困難になります。

方程式を解くための正しい、あるいは最良の方法はありませんが、実行可能なオプションはたくさんあります。 何十年にもわたって、渦度と流れ関数の観点からの再定式化、人工的な圧縮性の導入、演算子の分割など、この問題に対処するためのいくつかのアプローチが見つかりました。 Chorin（1969）、次にKim and Moin（1984、1990）は、非常に成功した人気のある分数ステップ法を定式化しました。これにより、暗黙的にではなく、圧力場を直接解きながら方程式を統合できます。 分数ステップ法は、演算子を分割することによって方程式を近似するための一般的な方法です。この場合は、圧力に沿って分割します。 このアプローチは比較的単純でありながら堅牢であり、ここでの選択の動機付けになります。

まず、ある時点から次の時点にステップすることができるように、方程式を時間内に数値的に離散化する必要があります。 Kim and Moin（1984）に続いて、対流項には2次明示的Adams-Bashforth法を使用し、粘性項には2次暗黙的Crank-Nicholson法を使用し、時間微分には単純な有限差分を使用します。 、圧力勾配を無視しながら。 これらの選択は、実行できる唯一の近似ではありません。それらの選択は、スキームの数値動作を制御することによってスキームを構築する際の技術の一部です。

これで中間速度を積分できますが、圧力の寄与を無視して発散します（非圧縮性では発散がない必要があります）。 オペレーターの残りの部分は、次のタイムステップに進むために必要です。

どこは、発散する自由速度をもたらすスカラーを見つけるために必要なスカラーです。 私たちは見つけることができます修正ステップの発散をとることによって、

ここで、最初の項は連続性によって要求されるようにゼロであり、次のタイムステップでソレノイド（発散のない）速度を提供するスカラー場のポアソン方程式を生成します。

キムとモイン（1984）が示すように、 は、オペレーターの分割の結果としての圧力ではありませんが、次のように見つけることができます。

チュートリアルのこの時点では、かなりうまくいっています。それらを統合できるように、支配方程式を一時的に識別しました。 ここで、演算子を空間的に区別する必要があります。 これを実現する方法はいくつかあります。たとえば、有限要素法、有限体積法、有限差分法などです。 Kim and Moin（1984）のオリジナル作品では、有限差分法を使用しています。 この方法は、比較的単純で計算効率が高いという点で有利ですが、構造化されたメッシュが必要なため、複雑な形状には問題があります。

有限要素法（FEM）は、その一般性のための便利な選択であり、その使用を支援するいくつかの非常に優れたオープンソースプロジェクトがあります。 特に、1次元、2次元、および3次元で実際の形状を処理し、マシンクラスターでの非常に大きな問題に対応し、高次の要素に比較的簡単に使用できます。 通常、この方法は3つのうち遅い方ですが、問題全体で最もマイレージが得られるため、ここで使用します。

FEMを実装する場合でも、多くの選択肢があります。 ここでは、GalerkinFEMを使用します。 そうすることで、それぞれにテスト関数を掛けることにより、重み付き残差形式で方程式をキャストします。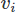 ベクトルと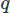スカラー場の場合、ドメイン全体で統合する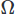。 次に、ストークの定理または発散定理を使用して、高階導関数の部分積分を実行します。 次に、変分問題を提起し、目的のCFDスキームを生成します。

これで、実装に「便利な」形式の優れた数学的スキームができました。うまくいけば、そこに到達するために何が必要かをある程度理解できます（多くの数学と、私たちがかなりコピーして微調整した優秀な研究者のメソッド）。