Przewodnik po obliczeniach naukowych z narzędziami Open Source

Historycznie, informatyka była w dużej mierze ograniczona do sfery naukowców i doktorantów. Jednak przez lata – być może bez wiedzy większej społeczności programistycznej – my, naukowcy zajmujący się obliczeniami jajowymi, po cichu kompilowaliśmy współpracujące biblioteki open-source, które obsługują zdecydowaną większość ciężkich zadań . W rezultacie implementacja modeli matematycznych jest teraz łatwiejsza niż kiedykolwiek i chociaż dziedzina może nie być jeszcze gotowa na masową konsumpcję, poprzeczka do udanej implementacji została drastycznie obniżona. Opracowanie nowej bazy kodu obliczeniowego od podstaw jest ogromnym przedsięwzięciem, mierzonym zwykle latami, ale te projekty naukowego przetwarzania danych typu open source umożliwiają uruchamianie dostępnych przykładów w celu stosunkowo szybkiego wykorzystania tych zdolności obliczeniowych.

Ponieważ celem obliczeń naukowych jest zapewnienie naukowego wglądu w rzeczywiste systemy, które istnieją w przyrodzie, dyscyplina ta stanowi przełom w sprawieniu, by oprogramowanie komputerowe zbliżyło się do rzeczywistości. Aby stworzyć oprogramowanie, które naśladuje rzeczywisty świat z bardzo wysokim stopniem zarówno dokładności, jak i rozdzielczości, należy odwołać się do złożonej matematyki różniczkowej, wymagającej wiedzy, która rzadko znajduje się poza murami uniwersytetów, krajowych laboratoriów lub korporacyjnych działów badawczo-rozwojowych. Ponadto, przy próbie opisania ciągłej, nieskończenie małej tkanki świata rzeczywistego przy użyciu dyskretnego języka zer i jedynek pojawiają się znaczące wyzwania liczbowe. Niezbędny jest wyczerpujący wysiłek i staranne przekształcenie numeryczne, aby wygenerować algorytmy, które są zarówno wykonalne obliczeniowo, jak i dają sensowne wyniki. Innymi słowy, informatyka naukowa jest ciężka.

Narzędzia Open Source do obliczeń naukowych

Osobiście szczególnie lubię projekt FEniCS, używając go do mojej pracy magisterskiej, i zademonstruję swoją stronniczość w wyborze tego do naszego przykładu kodu w tym samouczku. (Istnieją inne bardzo wysokiej jakości projekty, takie jak DUNE, z których również można skorzystać.)

FEniCS samookreśla się jako „wspólny projekt na rzecz rozwoju innowacyjnych koncepcji i narzędzi do zautomatyzowanych obliczeń naukowych, ze szczególnym naciskiem na zautomatyzowane rozwiązywanie równań różniczkowych metodami elementów skończonych”. Jest to potężna biblioteka do rozwiązywania ogromnej liczby problemów i naukowych zastosowań obliczeniowych. Wśród jego współtwórców znajdują się Simula Research Laboratory, University of Cambridge, University of Chicago, Baylor University i KTH Royal Institute of Technology, które wspólnie stworzyły bezcenny zasób w ciągu ostatniej dekady (patrz ciepło kodowe FEniCS).

Zadziwiające jest to, przed jakim wysiłkiem uchroniła nas biblioteka FEniCS. Aby zrozumieć niesamowitą głębię i zakres tematów, które obejmuje projekt, można zapoznać się z ich podręcznikiem typu open source, w którym Rozdział 21 porównuje nawet różne schematy elementów skończonych do rozwiązywania przepływów niekompresowalnych.

Za kulisami projekt zintegrował dla nas duży zestaw naukowych bibliotek obliczeniowych typu open source, które mogą być interesujące lub mogą być bezpośrednio użyte. Należą do nich, w dowolnej kolejności, projekty, które wywołuje projekt FEniCS:

• PETSc: Zestaw struktur danych i procedur do skalowalnego (równoległego) rozwiązania aplikacji naukowych modelowanych za pomocą równań różniczkowych cząstkowych.
• Projekt Trilinos: Zestaw niezawodnych algorytmów i technologii do rozwiązywania równań liniowych i nieliniowych, opracowany na podstawie pracy w Sandia National Labs.
• uBLAS: „Biblioteka klas szablonów C++, która zapewnia funkcjonalność BLAS poziomu 1, 2, 3 dla gęstych, upakowanych i rzadkich macierzy oraz wiele algorytmów numerycznych dla algebry liniowej”.
• GMP: Bezpłatna biblioteka do arytmetyki dowolnej precyzji, działająca na liczbach całkowitych ze znakiem, liczbach wymiernych i liczbach zmiennoprzecinkowych.
• UMFPACK: Zbiór procedur do rozwiązywania niesymetrycznych rozrzedzonych układów liniowych, Ax=b, przy użyciu metody Unsymmetric MultiFrontal.
• ParMETIS: Biblioteka równoległa oparta na MPI, która implementuje różne algorytmy do partycjonowania nieustrukturyzowanych grafów, siatek i do obliczania porządków redukujących wypełnienie w rzadkich macierzach.
• NumPy: podstawowy pakiet do obliczeń naukowych w Pythonie.
• CGAL: Wydajne i niezawodne algorytmy geometryczne w postaci biblioteki C++.
• SCOTCH: Pakiet oprogramowania i biblioteki do sekwencyjnego i równoległego partycjonowania grafów, statycznego mapowania i grupowania, sekwencyjnego partycjonowania siatek i hipergrafów oraz sekwencyjnego i równoległego porządkowania bloków macierzy rzadkich.
• MPI: ustandaryzowany i przenośny system przekazywania wiadomości zaprojektowany przez grupę naukowców ze środowisk akademickich i przemysłowych do działania na wielu różnych komputerach równoległych.
• VTK: Wolnodostępny system oprogramowania typu open source do grafiki komputerowej 3D, przetwarzania obrazu i wizualizacji.
• SLEPc: Biblioteka oprogramowania do rozwiązywania problemów z rzadkimi wartościami własnymi na dużą skalę na komputerach równoległych.

Ta lista zewnętrznych pakietów zintegrowanych z projektem daje nam wyobrażenie o jego odziedziczonych możliwościach. Na przykład zintegrowana obsługa MPI umożliwia skalowanie między pracownikami zdalnymi w środowisku klastra obliczeniowego (tj. ten kod będzie działał na superkomputerze lub laptopie).

Warto również zauważyć, że istnieje wiele zastosowań poza obliczeniami naukowymi, w których można by wykorzystać te projekty, w tym modelowanie finansowe, przetwarzanie obrazu, problemy z optymalizacją, a być może nawet gry wideo. Możliwe byłoby na przykład stworzenie gry wideo, która wykorzystuje niektóre z tych algorytmów i technik open source do rozwiązywania dwuwymiarowego przepływu płynu, takiego jak prądy oceaniczne/rzeczne, z którymi gracz mógłby wchodzić w interakcje (być może spróbować i przepłyń łodzią ze zmiennym wiatrem i przepływem wody).

Przykładowa aplikacja: wykorzystanie otwartego oprogramowania do obliczeń naukowych

Tutaj postaram się nadać przedsmak tego, na czym polega tworzenie modelu numerycznego, pokazując, jak podstawowy schemat obliczeniowej dynamiki płynów jest rozwijany i wdrażany w jednej z tych bibliotek open source - w tym przypadku w projekcie FEniCS. FEnICS dostarcza API zarówno w Pythonie jak i C++. W tym przykładzie użyjemy ich API Pythona.

Omówimy trochę raczej technicznych treści, ale celem będzie po prostu posmakowanie tego, co pociąga za sobą tworzenie takiego naukowego kodu obliczeniowego i jak wiele pracy wykonują dla nas dzisiejsze narzędzia open source. Miejmy nadzieję, że w tym procesie pomożemy w demistyfikacji złożonego świata obliczeń naukowych. (Zauważ, że dołączony jest dodatek, który zawiera szczegółowe informacje na temat wszystkich matematycznych i naukowych podstaw dla tych, którzy są zainteresowani tym poziomem szczegółowości.)

OŚWIADCZENIE: Dla tych czytelników, którzy mają niewielkie lub żadne doświadczenie w naukowym oprogramowaniu komputerowym i aplikacjach, części tego przykładu mogą sprawić, że poczujesz się tak:

Jeśli tak, nie rozpaczaj. Głównym wnioskiem jest to, w jakim stopniu istniejące projekty open source mogą znacznie uprościć wiele z tych zadań.

Mając to na uwadze, zacznijmy od obejrzenia wersji demonstracyjnej FEnICS dla nieściśliwych Navier-Stokes. To demo modeluje ciśnienie i prędkość nieściśliwego płynu przepływającego przez kolanko w kształcie litery L, takie jak rura kanalizacyjna.

Opis na stronie demonstracyjnej, do której prowadzi link, zapewnia doskonałą, zwięzłą konfigurację niezbędnych kroków do uruchomienia kodu i zachęcam do szybkiego spojrzenia, aby zobaczyć, co się z tym wiąże. Podsumowując, demo rozwiąże prędkość i ciśnienie w zakręcie dla nieściśliwych równań przepływu. Demo przeprowadza krótką symulację przepływu płynu w czasie, animując wyniki na bieżąco. Jest to osiągane przez ustawienie siatki reprezentującej przestrzeń w rurze i użycie metody elementów skończonych do liczbowego obliczenia prędkości i ciśnienia w każdym punkcie siatki. Następnie iterujemy w czasie, aktualizując pola prędkości i ciśnienia w miarę upływu czasu, ponownie korzystając z równań, które mamy do dyspozycji.

Demo działa dobrze, ale zamierzamy je nieco zmodyfikować. Demo wykorzystuje podział Chorin, ale zamiast tego użyjemy nieco innej metody inspirowanej przez Kim i Moin, która, mamy nadzieję, będzie bardziej stabilna. Wymaga to tylko zmiany równania używanego do aproksymacji wyrazów konwekcyjnych i lepkich, ale aby to zrobić, musimy zapisać pole prędkości z poprzedniego kroku czasowego i dodać dwa dodatkowe wyrazy do równania aktualizacji, które użyje tego poprzedniego informacje dla dokładniejszego przybliżenia liczbowego.

Więc dokonajmy tej zmiany. Najpierw dodajemy nowy obiekt Function do konfiguracji. Jest to obiekt reprezentujący abstrakcyjną funkcję matematyczną, taką jak pole wektorowe lub skalarne. Nazwiemy to un1 będzie przechowywać poprzednie pole prędkości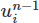 na naszej przestrzeni funkcyjnej V .

 ... # Create functions (three distinct vector fields and a scalar field) un1 = Function(V) # the previous time step's velocity field we are adding u0 = Function(V) # the current velocity field u1 = Function(V) # the next velocity field (what's being solved for) p1 = Function(Q) # the next pressure field (what's being solved for) ...

Następnie musimy zmienić sposób, w jaki „prędkość wstępna” jest aktualizowana na każdym etapie symulacji. To pole reprezentuje przybliżoną prędkość w następnym kroku czasowym, gdy ciśnienie jest ignorowane (w tym momencie ciśnienie nie jest jeszcze znane). W tym miejscu zastępujemy metodę podziału Chorina nowszą metodą kroku ułamkowego Kima i Moina. Innymi słowy zmienimy wyrażenie dla pola F1 :

Zastępować:

 # Tentative velocity field (a first prediction of what the next velocity field is) # for the Chorin style split # F1 = change in the velocity field + # convective term + # diffusive term - # body force term F1 = (1/k)*inner(u - u0, v)*dx + \ inner(grad(u0)*u0, v)*dx + \ nu*inner(grad(u), grad(v))*dx - \ inner(f, v)*dx

Z:

 # Tentative velocity field (a first prediction of what the next velocity field is) # for the Kim and Moin style split # F1 = change in the velocity field + # convective term + # diffusive term - # body force term F1 = (1/k)*inner(u - u0, v)*dx + \ (3.0/2.0) * inner(grad(u0)*u0, v)*dx - (1.0/2.0) * inner(grad(un1)*un1, v)*dx + \ (nu/2.0)*inner(grad(u+u0), grad(v))*dx - \ inner(f, v)*dx

więc demo używa teraz naszej zaktualizowanej metody rozwiązywania dla pola prędkości pośredniej, gdy używa F1 .

Na koniec upewnij się, że aktualizujemy poprzednie pole prędkości, un1 , na końcu każdego kroku iteracji

 ... # Move to next time step un1.assign(u0) # copy the current velocity field into the previous velocity field u0.assign(u1) # copy the next velocity field into the current velocity field ...

Oto kompletny kod z naszego demo FEniCS CFD, wraz z naszymi zmianami:

 """This demo program solves the incompressible Navier-Stokes equations on an L-shaped domain using Kim and Moin's fractional step method.""" # Begin demo from dolfin import * # Print log messages only from the root process in parallel parameters["std_out_all_processes"] = False; # Load mesh from file mesh = Mesh("lshape.xml.gz") # Define function spaces (P2-P1) V = VectorFunctionSpace(mesh, "Lagrange", 2) Q = FunctionSpace(mesh, "Lagrange", 1) # Define trial and test functions u = TrialFunction(V) p = TrialFunction(Q) v = TestFunction(V) q = TestFunction(Q) # Set parameter values dt = 0.01 T = 3 nu = 0.01 # Define time-dependent pressure boundary condition p_in = Expression("sin(3.0*t)", t=0.0) # Define boundary conditions noslip = DirichletBC(V, (0, 0), "on_boundary && \ (x[0] < DOLFIN_EPS | x[1] < DOLFIN_EPS | \ (x[0] > 0.5 - DOLFIN_EPS && x[1] > 0.5 - DOLFIN_EPS))") inflow = DirichletBC(Q, p_in, "x[1] > 1.0 - DOLFIN_EPS") outflow = DirichletBC(Q, 0, "x[0] > 1.0 - DOLFIN_EPS") bcu = [noslip] bcp = [inflow, outflow] # Create functions un1 = Function(V) u0 = Function(V) u1 = Function(V) p1 = Function(Q) # Define coefficients k = Constant(dt) f = Constant((0, 0)) # Tentative velocity field (a first prediction of what the next velocity field is) # for the Kim and Moin style split # F1 = change in the velocity field + # convective term + # diffusive term - # body force term F1 = (1/k)*inner(u - u0, v)*dx + \ (3.0/2.0) * inner(grad(u0)*u0, v)*dx - (1.0/2.0) * inner(grad(un1)*un1, v)*dx + \ (nu/2.0)*inner(grad(u+u0), grad(v))*dx - \ inner(f, v)*dx a1 = lhs(F1) L1 = rhs(F1) # Pressure update a2 = inner(grad(p), grad(q))*dx L2 = -(1/k)*div(u1)*q*dx # Velocity update a3 = inner(u, v)*dx L3 = inner(u1, v)*dx - k*inner(grad(p1), v)*dx # Assemble matrices A1 = assemble(a1) A2 = assemble(a2) A3 = assemble(a3) # Use amg preconditioner if available prec = "amg" if has_krylov_solver_preconditioner("amg") else "default" # Create files for storing solution ufile = File("results/velocity.pvd") pfile = File("results/pressure.pvd") # Time-stepping t = dt while t < T + DOLFIN_EPS: # Update pressure boundary condition p_in.t = t # Compute tentative velocity step begin("Computing tentative velocity") b1 = assemble(L1) [bc.apply(A1, b1) for bc in bcu] solve(A1, u1.vector(), b1, "gmres", "default") end() # Pressure correction begin("Computing pressure correction") b2 = assemble(L2) [bc.apply(A2, b2) for bc in bcp] solve(A2, p1.vector(), b2, "cg", prec) end() # Velocity correction begin("Computing velocity correction") b3 = assemble(L3) [bc.apply(A3, b3) for bc in bcu] solve(A3, u1.vector(), b3, "gmres", "default") end() # Plot solution plot(p1, title="Pressure", rescale=True) plot(u1, title="Velocity", rescale=True) # Save to file ufile << u1 pfile << p1 # Move to next time step un1.assign(u0) u0.assign(u1) t += dt print "t =", t # Hold plot interactive()

Uruchomienie programu pokazuje przepływ wokół kolanka. Uruchom sam kod obliczeniowy, aby zobaczyć, jak jest animowany! Poniżej przedstawiamy ekrany końcowej klatki.

Naciski względne w zakręcie na końcu symulacji, przeskalowane i pokolorowane według wielkości (wartości bezwymiarowe):

Prędkości względne w zakręcie na końcu symulacji jako glify wektorowe skalowane i kolorowane według wielkości (wartości bezwymiarowe).

Tak więc zrobiliśmy istniejące demo, które dość łatwo zaimplementowaliśmy schemat bardzo podobny do naszego, i zmodyfikowaliśmy je tak, aby używało lepszych przybliżeń, wykorzystując informacje z poprzedniego kroku czasowego.

W tym momencie możesz pomyśleć, że to trywialna zmiana. Tak było iw dużej mierze o to chodzi. Ten projekt obliczeń naukowych o otwartym kodzie źródłowym pozwolił nam szybko zaimplementować zmodyfikowany model numeryczny poprzez zmianę czterech linijek kodu. Takie zmiany mogą zająć miesiące w dużych kodach badawczych.

Projekt ma wiele innych wersji demonstracyjnych, które można wykorzystać jako punkt wyjścia. Istnieje nawet szereg aplikacji open source zbudowanych na projekcie, które implementują różne modele.

Wniosek

Obliczenia naukowe i ich zastosowania są rzeczywiście złożone. Nie da się tego obejść. Ale, jak to jest coraz bardziej prawdziwe w wielu dziedzinach, stale rosnący krajobraz dostępnych narzędzi i projektów open source może znacznie uprościć to, co w innym przypadku byłoby niezwykle skomplikowane i żmudne zadania programistyczne. Być może zbliża się nawet czas, w którym obliczenia naukowe staną się wystarczająco dostępne, aby można je było łatwo wykorzystać poza społecznością badawczą.

DODATEK: Podstawy naukowe i matematyczne

Dla zainteresowanych, oto techniczne podstawy naszego przewodnika po obliczeniowej dynamice płynów powyżej. Poniższe informacje posłużą jako bardzo przydatne i zwięzłe podsumowanie tematów, które są zwykle poruszane w trakcie kilkunastu kursów na poziomie magisterskim. Absolwenci i typy matematyczne zainteresowane głębokim zrozumieniem tematu mogą uznać ten materiał za dość interesujący.

Mechanika płynów

Ogólnie rzecz biorąc, „modelowanie” jest procesem rozwiązywania pewnego rzeczywistego systemu za pomocą przybliżeń szeregowych. Model będzie często zawierał równania ciągłe nieodpowiednie do implementacji komputerowej, dlatego musi być dalej aproksymowany metodami numerycznymi.

W przypadku mechaniki płynów zacznijmy ten przewodnik od podstawowych równań, równań Naviera-Stokesa i wykorzystajmy je do opracowania schematu CFD.

Równania Naviera-Stokesa są serią równań różniczkowych cząstkowych (PDE), które bardzo dobrze opisują przepływy płynów, a zatem są naszym punktem wyjścia. Można je wyprowadzić z praw zachowania masy, pędu i energii rzuconych przez twierdzenie o transporcie Reynoldsa i stosując twierdzenie Gaussa i powołując się na hipotezę Stoke'a. Równania wymagają założenia kontinuum, gdzie zakłada się, że mamy wystarczającą ilość cząstek płynu, aby nadać właściwości statystyczne, takie jak temperatura, gęstość i prędkość. Ponadto potrzebna jest liniowa zależność między tensorem naprężeń powierzchniowych a tensorem szybkości odkształcenia, symetria w tensorze naprężeń oraz założenia dotyczące płynu izotropowego. Ważne jest, aby znać założenia, które przyjmujemy i dziedziczymy podczas tego rozwoju, abyśmy mogli ocenić możliwość zastosowania w otrzymanym kodzie. Równania Naviera-Stokesa w notacji Einsteina, bez zbędnych ceregieli:

Ochrona masy:

Zachowanie pędu:

Oszczędzanie energii:

gdzie naprężenie dewiatoryczne to:

Chociaż są bardzo ogólne, regulują większość przepływów płynów w świecie fizycznym, nie są one bezpośrednio przydatne. Istnieje stosunkowo niewiele znanych dokładnych rozwiązań równań, a nagroda milenijna w wysokości 1 000 000 USD jest dostępna dla każdego, kto może rozwiązać problem istnienia i gładkości. Ważną częścią jest to, że mamy punkt wyjścia do rozwoju naszego modelu poprzez szereg założeń w celu zmniejszenia złożoności (są to jedne z najtrudniejszych równań w fizyce klasycznej).

Aby wszystko było „proste”, użyjemy naszej wiedzy specyficznej dla danej dziedziny, aby przyjąć nieściśliwe założenia dotyczące płynu i założyć stałe temperatury, tak że zachowanie równania energii, które staje się równaniem ciepła, nie jest potrzebne (oddzielone). Mamy teraz dwa równania, wciąż PDE, ale znacznie prostsze, a jednocześnie rozwiązujące dużą liczbę rzeczywistych problemów z płynami.

Równanie ciągłości

Równania pędu

W tym momencie mamy teraz ładny model matematyczny dla przepływów nieściśliwych płynów (na przykład gazy i ciecze o niskiej prędkości, takie jak woda). Ręczne rozwiązywanie tych równań nie jest łatwe, ale jest przyjemne, ponieważ możemy uzyskać „dokładne” rozwiązania prostych problemów. Korzystanie z tych równań do rozwiązywania interesujących problemów, na przykład powietrza przepływającego nad skrzydłem lub wody przepływającej przez jakiś system, wymaga rozwiązania tych równań numerycznie.

Budowanie schematu numerycznego

Aby rozwiązywać bardziej złożone problemy za pomocą komputera, potrzebna jest metoda numerycznego rozwiązywania naszych nieściśliwych równań. Rozwiązywanie równań różniczkowych cząstkowych, a nawet równań różniczkowych, numerycznie nie jest trywialne. Jednak nasze równania w tym przewodniku mają szczególne wyzwanie (niespodzianka!). Oznacza to, że musimy rozwiązać równania pędu, zachowując rozbieżność rozwiązania, zgodnie z wymogami ciągłości. Prosta integracja czasu za pomocą czegoś takiego jak metoda Rungego-Kutty jest trudna, ponieważ równanie ciągłości nie zawiera w sobie pochodnej po czasie.

Nie ma poprawnej, a nawet najlepszej metody rozwiązywania równań, ale istnieje wiele praktycznych opcji. Przez dziesięciolecia znaleziono kilka podejść do rozwiązania tego problemu, takich jak przeformułowanie pod kątem wirowości i funkcji strumienia, wprowadzenie sztucznej ściśliwości i dzielenie operatorów. Chorin (1969), a następnie Kim i Moin (1984, 1990), sformułowali bardzo udaną i popularną metodę kroku ułamkowego, która pozwoli nam na całkowanie równań podczas rozwiązywania pola ciśnienia bezpośrednio, a nie pośrednio. Metoda kroku ułamkowego jest ogólną metodą aproksymacji równań przez rozdzielenie ich operatorów, w tym przypadku rozdzielenie wzdłuż ciśnienia. Podejście jest stosunkowo proste, a jednocześnie solidne, co motywuje jego wybór tutaj.

Najpierw musimy numerycznie rozdzielić równania w czasie, abyśmy mogli przejść z jednego punktu w czasie do następnego. Idąc za Kim i Moinem (1984), użyjemy jawnej metody drugiego rzędu Adamsa-Bashfortha dla warunków konwekcyjnych, niejawnej metody drugiego rzędu Cranka-Nicholsona dla warunków lepkich, prostej różnicy skończonej dla pochodnej czasowej , pomijając gradient ciśnienia. Te wybory w żadnym wypadku nie są jedynymi przybliżeniami, jakich można dokonać: ich wybór jest częścią sztuki budowania schematu poprzez kontrolowanie zachowania liczbowego schematu.

Pośrednią prędkość można teraz całkować, jednak ignoruje ona udział ciśnienia i jest teraz rozbieżna (nieściśliwość wymaga, aby była rozbieżna). Pozostała część operatora jest potrzebna, aby doprowadzić nas do następnego kroku czasowego.

gdzie jest jakimś skalarem, który musimy znaleźć, co skutkuje rozbieżną prędkością swobodną. Możemy znaleźć przyjmując rozbieżność kroku korekcyjnego,

gdzie pierwszy składnik wynosi zero, zgodnie z wymogami ciągłości, dając równanie Poissona dla pola skalarnego, które zapewni prędkość solenoidu (swobodną rozbieżną) w następnym kroku czasowym.

Jak pokazują Kim i Moin (1984), nie jest dokładnie ciśnieniem w wyniku rozłupywania operatora, ale można go znaleźć przez:

Na tym etapie samouczka radzimy sobie całkiem nieźle, czasowo zdystrybuowaliśmy rządzące równania, aby móc je zintegrować. Musimy teraz przestrzennie zdyskrytyzować operatorów. Istnieje wiele metod, za pomocą których możemy to osiągnąć, na przykład Metoda Elementów Skończonych, Metoda Objętości Skończonych i Metoda Różnic Skończonych. W oryginalnej pracy Kima i Moina (1984) posługują się oni Metodą Różnic Skończonych. Metoda jest korzystna ze względu na swoją względną prostotę i wydajność obliczeniową, ale cierpi na złożoną geometrię, ponieważ wymaga ustrukturyzowanej siatki.

Metoda elementów skończonych (MES) jest wygodnym wyborem ze względu na jej ogólność i ma kilka bardzo ładnych projektów open source, które pomagają w jej użyciu. W szczególności obsługuje rzeczywiste geometrie w jednym, dwóch i trzech wymiarach, skale dla bardzo dużych problemów na klastrach maszyn i jest stosunkowo łatwy w użyciu dla elementów wysokiego rzędu. Zazwyczaj ta metoda jest wolniejsza z tych trzech, jednak da nam najwięcej kilometrów przez problemy, więc użyjemy jej tutaj.

Nawet przy wdrażaniu MES istnieje wiele możliwości wyboru. Tutaj użyjemy Galerkin MES. W ten sposób rzucamy równania w postaci ważonej reszty, mnożąc każde przez funkcję testową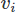 dla wektorów i 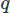dla pola skalarnego i całkowania po domenie 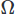. Następnie przeprowadzamy częściowe całkowanie na dowolnych pochodnych wysokiego rzędu, korzystając z twierdzenia Stoke'a lub twierdzenia o dywergencji. Następnie stawiamy problem wariacyjny, uzyskując pożądany schemat CFD.

Mamy teraz fajny schemat matematyczny w „wygodnej” formie do wdrożenia, miejmy nadzieję, że z pewnym wyczuciem tego, co było potrzebne, aby się tam dostać (mnóstwo matematyki i metod od genialnych badaczy, które w dużej mierze kopiujemy i ulepszamy).