Руководство по научным вычислениям с помощью инструментов с открытым исходным кодом

Исторически сложилось так, что вычислительная наука в основном ограничивалась областью ученых-исследователей и докторантов. Однако на протяжении многих лет — возможно, без ведома более широкого сообщества разработчиков программного обеспечения — мы, умные головы в области научных вычислений, незаметно компилировали совместные библиотеки с открытым исходным кодом, которые справляются с подавляющим большинством тяжелой работы . В результате теперь реализовать математические модели стало проще, чем когда-либо, и, хотя эта область еще не готова к массовому потреблению, планка успешного внедрения была резко снижена. Разработка новой вычислительной кодовой базы с нуля — это огромная задача, обычно измеряемая годами, но эти проекты научных вычислений с открытым исходным кодом позволяют работать с доступными примерами, чтобы относительно быстро использовать эти вычислительные возможности.

Поскольку цель научных вычислений состоит в том, чтобы обеспечить научное понимание реальных систем, существующих в природе, эта дисциплина представляет собой передний край в приближении компьютерного программного обеспечения к реальности. Чтобы создать программное обеспечение, которое имитирует реальный мир с очень высокой степенью точности и разрешения, необходимо использовать сложную дифференциальную математику, требующую знаний, которые редко можно найти за стенами университетов, национальных лабораторий или корпоративных отделов исследований и разработок. Вдобавок ко всему, при попытке описать непрерывную, бесконечно малую ткань реального мира, используя дискретный язык нулей и единиц, возникают серьезные числовые проблемы. Исчерпывающие усилия по тщательному численному преобразованию необходимы для визуализации алгоритмов, которые одновременно поддаются вычислительной обработке и дают значимые результаты. Другими словами, научные вычисления — это тяжелая работа.

Инструменты с открытым исходным кодом для научных вычислений

Лично мне особенно нравится проект FEniCS, поскольку я использую его для своей дипломной работы, и я продемонстрирую свою предвзятость, выбрав его для нашего примера кода для этого руководства. (Есть и другие очень качественные проекты, такие как DUNE, которые тоже можно использовать.)

FEniCS описывается как «совместный проект по разработке инновационных концепций и инструментов для автоматизированных научных вычислений с особым акцентом на автоматизированное решение дифференциальных уравнений методами конечных элементов». Это мощная библиотека для решения огромного количества задач и приложений для научных вычислений. В его состав входят Исследовательская лаборатория Simula, Кембриджский университет, Чикагский университет, Университет Бэйлора и Королевский технологический институт KTH, которые вместе превратили его в бесценный ресурс в течение последнего десятилетия (см. codewarm FEniCS).

Что довольно удивительно, так это то, от каких усилий нас оградила библиотека FEniCS. Чтобы получить представление об удивительной глубине и широте тем, охватываемых проектом, можно просмотреть их учебник с открытым исходным кодом, где в главе 21 даже сравниваются различные схемы конечных элементов для решения несжимаемых течений.

За кулисами проект интегрировал для нас большой набор библиотек для научных вычислений с открытым исходным кодом, которые могут представлять интерес или использоваться напрямую. К ним относятся, в произвольном порядке, проекты, которые называет проект FEniCS:

• PETSc: набор структур данных и подпрограмм для масштабируемого (параллельного) решения научных приложений, моделируемых уравнениями в частных производных.
• Проект Trilinos: набор надежных алгоритмов и технологий для решения как линейных, так и нелинейных уравнений, разработанный на основе работы в Sandia National Labs.
• uBLAS: «Библиотека классов шаблонов C++, обеспечивающая функциональность уровня 1, 2, 3 BLAS для плотных, упакованных и разреженных матриц и многих числовых алгоритмов для линейной алгебры».
• GMP: бесплатная библиотека для арифметики произвольной точности, работающая с целыми числами со знаком, рациональными числами и числами с плавающей запятой.
• UMFPACK: набор подпрограмм для решения несимметричных разреженных линейных систем, Ax=b, с использованием метода несимметричного мультифронтала.
• ParMETIS: параллельная библиотека на основе MPI, которая реализует множество алгоритмов для разбиения неструктурированных графов, сеток и для вычисления порядка заполнения разреженных матриц.
• NumPy: основной пакет для научных вычислений с Python.
• CGAL: эффективные и надежные геометрические алгоритмы в виде библиотеки C++.
• SCOTCH: пакет программного обеспечения и библиотеки для последовательного и параллельного разбиения графа, статического отображения и кластеризации, последовательного разбиения сетки и гиперграфа, а также последовательного и параллельного упорядочения блоков разреженной матрицы.
• MPI: стандартизированная и портативная система передачи сообщений, разработанная группой исследователей из академических кругов и промышленности для работы на самых разных параллельных компьютерах.
• VTK: свободно доступная программная система с открытым исходным кодом для трехмерной компьютерной графики, обработки изображений и визуализации.
• SLEPc: программная библиотека для решения крупномасштабных разреженных задач на собственные значения на параллельных компьютерах.

Этот список внешних пакетов, интегрированных в проект, дает нам представление о его унаследованных возможностях. Например, встроенная поддержка MPI позволяет масштабировать работу удаленных сотрудников в среде вычислительного кластера (т. е. этот код будет выполняться на суперкомпьютере или ноутбуке).

Также интересно отметить, что существует множество приложений помимо научных вычислений, для которых эти проекты могут быть использованы, включая финансовое моделирование, обработку изображений, задачи оптимизации и, возможно, даже видеоигры. Например, можно было бы создать видеоигру, использующую некоторые из этих алгоритмов и методов с открытым исходным кодом для расчета двухмерных течений жидкости, таких как океанские/речные течения, с которыми игрок будет взаимодействовать (возможно, попробует и плыть на лодке с переменным ветром и течением воды).

Пример приложения: использование открытого исходного кода для научных вычислений

Здесь я попытаюсь дать представление о том, что включает в себя разработка численной модели, показав, как базовая схема вычислительной гидродинамики разрабатывается и реализуется в одной из этих библиотек с открытым исходным кодом — в данном случае в проекте FEniCS. FEnICS предоставляет API как на Python, так и на C++. В этом примере мы будем использовать их Python API.

Мы обсудим некоторый довольно технический контент, но цель будет заключаться в том, чтобы просто дать представление о том, что влечет за собой разработка такого научного вычислительного кода, и сколько работы делают для нас сегодняшние инструменты с открытым исходным кодом. Надеемся, что в процессе мы поможем демистифицировать сложный мир научных вычислений. (Обратите внимание, что для тех, кто интересуется этим уровнем детализации, имеется Приложение, в котором подробно описаны все математические и научные обоснования.)

ОТКАЗ ОТ ОТВЕТСТВЕННОСТИ: Для тех читателей, у которых мало или вообще нет опыта работы с программным обеспечением и приложениями для научных вычислений, части этого примера могут вызвать у вас следующие чувства:

Если да, не отчаивайтесь. Основным выводом здесь является то, насколько существующие проекты с открытым исходным кодом могут значительно упростить многие из этих задач.

Имея это в виду, давайте начнем с демонстрации несжимаемой модели Навье-Стокса в FEnICS. Эта демонстрация моделирует давление и скорость несжимаемой жидкости, протекающей через L-образный изгиб, такой как водопроводная труба.

Описание на связанной демонстрационной странице дает превосходную краткую настройку необходимых шагов для запуска кода, и я рекомендую вам быстро просмотреть, что происходит. Подводя итог, демонстрация будет решать скорость и давление через изгиб для уравнений потока несжимаемой жидкости. Демонстрация запускает короткую симуляцию течения жидкости во времени, анимируя результаты по ходу движения. Это достигается путем настройки сетки, представляющей пространство в трубе, и использования метода конечных элементов для численного решения скорости и давления в каждой точке сетки. Затем мы итерируемся во времени, обновляя поля скорости и давления по мере продвижения, снова используя имеющиеся в нашем распоряжении уравнения.

Демонстрация работает хорошо, но мы ее немного изменим. В демоверсии используется разделение Chorin, но вместо этого мы собираемся использовать немного другой метод, вдохновленный Kim и Moin, который, как мы надеемся, более стабилен. Это просто требует, чтобы мы изменили уравнение, используемое для аппроксимации конвективных и вязких членов, но для этого нам нужно сохранить поле скоростей предыдущего временного шага и добавить два дополнительных члена в уравнение обновления, которое будет использовать это предыдущее информацию для более точного численного приближения.

Итак, давайте внесем это изменение. Во-первых, мы добавляем в настройку новый объект Function . Это объект, представляющий абстрактную математическую функцию, такую ​​как векторное или скалярное поле. Мы назовем его un1 , он будет хранить предыдущее поле скорости.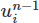 на нашем функциональном пространстве V .

 ... # Create functions (three distinct vector fields and a scalar field) un1 = Function(V) # the previous time step's velocity field we are adding u0 = Function(V) # the current velocity field u1 = Function(V) # the next velocity field (what's being solved for) p1 = Function(Q) # the next pressure field (what's being solved for) ...

Затем нам нужно изменить способ обновления «предварительной скорости» на каждом этапе моделирования. Это поле представляет приблизительную скорость на следующем временном шаге, когда давление игнорируется (в этот момент давление еще неизвестно). Именно здесь мы заменяем метод разделения Чорина на более новый метод дробного шага Кима и Мойна. Другими словами, изменим выражение для поля F1 :

Заменять:

 # Tentative velocity field (a first prediction of what the next velocity field is) # for the Chorin style split # F1 = change in the velocity field + # convective term + # diffusive term - # body force term F1 = (1/k)*inner(u - u0, v)*dx + \ inner(grad(u0)*u0, v)*dx + \ nu*inner(grad(u), grad(v))*dx - \ inner(f, v)*dx

С участием:

 # Tentative velocity field (a first prediction of what the next velocity field is) # for the Kim and Moin style split # F1 = change in the velocity field + # convective term + # diffusive term - # body force term F1 = (1/k)*inner(u - u0, v)*dx + \ (3.0/2.0) * inner(grad(u0)*u0, v)*dx - (1.0/2.0) * inner(grad(un1)*un1, v)*dx + \ (nu/2.0)*inner(grad(u+u0), grad(v))*dx - \ inner(f, v)*dx

так что демо теперь использует наш обновленный метод для решения для промежуточного поля скоростей, когда он использует F1 .

Наконец, убедитесь, что мы обновляем предыдущее поле скорости un1 в конце каждого шага итерации.

 ... # Move to next time step un1.assign(u0) # copy the current velocity field into the previous velocity field u0.assign(u1) # copy the next velocity field into the current velocity field ...

Итак, ниже приведен полный код из нашей демонстрации FEniCS CFD с включенными нашими изменениями:

 """This demo program solves the incompressible Navier-Stokes equations on an L-shaped domain using Kim and Moin's fractional step method.""" # Begin demo from dolfin import * # Print log messages only from the root process in parallel parameters["std_out_all_processes"] = False; # Load mesh from file mesh = Mesh("lshape.xml.gz") # Define function spaces (P2-P1) V = VectorFunctionSpace(mesh, "Lagrange", 2) Q = FunctionSpace(mesh, "Lagrange", 1) # Define trial and test functions u = TrialFunction(V) p = TrialFunction(Q) v = TestFunction(V) q = TestFunction(Q) # Set parameter values dt = 0.01 T = 3 nu = 0.01 # Define time-dependent pressure boundary condition p_in = Expression("sin(3.0*t)", t=0.0) # Define boundary conditions noslip = DirichletBC(V, (0, 0), "on_boundary && \ (x[0] < DOLFIN_EPS | x[1] < DOLFIN_EPS | \ (x[0] > 0.5 - DOLFIN_EPS && x[1] > 0.5 - DOLFIN_EPS))") inflow = DirichletBC(Q, p_in, "x[1] > 1.0 - DOLFIN_EPS") outflow = DirichletBC(Q, 0, "x[0] > 1.0 - DOLFIN_EPS") bcu = [noslip] bcp = [inflow, outflow] # Create functions un1 = Function(V) u0 = Function(V) u1 = Function(V) p1 = Function(Q) # Define coefficients k = Constant(dt) f = Constant((0, 0)) # Tentative velocity field (a first prediction of what the next velocity field is) # for the Kim and Moin style split # F1 = change in the velocity field + # convective term + # diffusive term - # body force term F1 = (1/k)*inner(u - u0, v)*dx + \ (3.0/2.0) * inner(grad(u0)*u0, v)*dx - (1.0/2.0) * inner(grad(un1)*un1, v)*dx + \ (nu/2.0)*inner(grad(u+u0), grad(v))*dx - \ inner(f, v)*dx a1 = lhs(F1) L1 = rhs(F1) # Pressure update a2 = inner(grad(p), grad(q))*dx L2 = -(1/k)*div(u1)*q*dx # Velocity update a3 = inner(u, v)*dx L3 = inner(u1, v)*dx - k*inner(grad(p1), v)*dx # Assemble matrices A1 = assemble(a1) A2 = assemble(a2) A3 = assemble(a3) # Use amg preconditioner if available prec = "amg" if has_krylov_solver_preconditioner("amg") else "default" # Create files for storing solution ufile = File("results/velocity.pvd") pfile = File("results/pressure.pvd") # Time-stepping t = dt while t < T + DOLFIN_EPS: # Update pressure boundary condition p_in.t = t # Compute tentative velocity step begin("Computing tentative velocity") b1 = assemble(L1) [bc.apply(A1, b1) for bc in bcu] solve(A1, u1.vector(), b1, "gmres", "default") end() # Pressure correction begin("Computing pressure correction") b2 = assemble(L2) [bc.apply(A2, b2) for bc in bcp] solve(A2, p1.vector(), b2, "cg", prec) end() # Velocity correction begin("Computing velocity correction") b3 = assemble(L3) [bc.apply(A3, b3) for bc in bcu] solve(A3, u1.vector(), b3, "gmres", "default") end() # Plot solution plot(p1, title="Pressure", rescale=True) plot(u1, title="Velocity", rescale=True) # Save to file ufile << u1 pfile << p1 # Move to next time step un1.assign(u0) u0.assign(u1) t += dt print "t =", t # Hold plot interactive()

Запуск программы показывает обтекание локтя. Запустите код научных вычислений самостоятельно, чтобы увидеть его анимацию! Скрин финального кадра представлен ниже.

Относительные давления в изгибе в конце моделирования, масштабированные и окрашенные по величине (безразмерные значения):

Относительные скорости в изгибе в конце симуляции в виде векторных глифов, масштабированных и окрашенных по величине (безразмерные значения).

Итак, что мы сделали, так это взяли существующую демонстрацию, которая довольно легко реализует схему, очень похожую на нашу, и модифицировали ее, чтобы использовать лучшие приближения, используя информацию из предыдущего временного шага.

В этот момент вы можете подумать, что это было тривиальное редактирование. Так и было, и в этом, по большому счету, дело. Этот проект научных вычислений с открытым исходным кодом позволил нам быстро реализовать модифицированную численную модель, изменив четыре строки кода. Такие изменения могут занять месяцы в крупных исследовательских кодах.

В проекте есть много других демонстраций, которые можно использовать в качестве отправной точки. Существует даже ряд приложений с открытым исходным кодом, созданных на основе проекта, которые реализуют различные модели.

Заключение

Научные вычисления и их приложения действительно сложны. Там нет обойти это. Но, как это становится все более верным во многих областях, постоянно растущий ландшафт доступных инструментов и проектов с открытым исходным кодом может значительно упростить то, что в противном случае было бы чрезвычайно сложным и утомительным заданием программирования. И, возможно, даже близко то время, когда научные вычисления станут достаточно доступными, чтобы их можно было легко использовать за пределами исследовательского сообщества.

ПРИЛОЖЕНИЕ: Научные и математические основы

Для тех, кто заинтересован, вот технические основы нашего руководства по вычислительной гидродинамике выше. То, что следует ниже, послужит очень полезным и кратким изложением тем, которые обычно рассматриваются в течение дюжины или около того курсов для выпускников. Аспиранты и математические типы, заинтересованные в глубоком понимании темы, могут найти этот материал весьма интересным.

Гидромеханика

«Моделирование» в общем случае — это процесс решения некоторой реальной системы с помощью ряда приближений. Модель часто будет включать непрерывные уравнения, плохо подходящие для компьютерной реализации, и поэтому ее необходимо дополнительно аппроксимировать численными методами.

Для гидромеханики давайте начнем это руководство с фундаментальных уравнений, уравнений Навье-Стокса, и используем их для разработки схемы CFD.

Уравнения Навье-Стокса представляют собой ряд дифференциальных уравнений в частных производных (УЧП), которые очень хорошо описывают потоки жидкости и поэтому являются нашей отправной точкой. Они могут быть получены из законов сохранения массы, импульса и энергии, брошенных через транспортную теорему Рейнольдса, применяя теорему Гаусса и ссылаясь на гипотезу Стокса. Уравнения требуют предположения о континууме, когда предполагается, что у нас достаточно жидких частиц, чтобы придать статистические свойства, такие как температура, плотность и значение скорости. Кроме того, необходимы линейная связь между тензором поверхностных напряжений и тензором скорости деформации, симметрия тензора напряжений и предположения об изотропной жидкости. Важно знать предположения, которые мы делаем и наследуем во время этой разработки, чтобы мы могли оценить применимость полученного кода. Уравнения Навье-Стокса в обозначениях Эйнштейна, без лишних слов:

Сохранение массы:

Сохранение импульса:

Сохранение энергии:

где девиаторное напряжение:

Хотя они очень общие и управляют большинством потоков жидкости в физическом мире, они не очень полезны напрямую. Известно относительно немного точных решений уравнений, и каждому, кто решит проблему существования и гладкости, присуждается премия тысячелетия в размере 1 000 000 долларов. Важно то, что у нас есть отправная точка для разработки нашей модели, сделав ряд допущений для уменьшения сложности (это одни из самых сложных уравнений в классической физике).

Чтобы все было «просто», мы будем использовать наши знания в предметной области, чтобы сделать предположение о несжимаемости жидкости и предположить постоянную температуру, так что уравнение сохранения энергии, которое становится уравнением теплоты, не требуется (разделено). Теперь у нас есть два уравнения, все еще УЧП, но значительно более простые, но по-прежнему решающие большое количество задач с реальными жидкостями.

Уравнение непрерывности

Уравнения импульса

На данный момент у нас теперь есть хорошая математическая модель потоков несжимаемой жидкости (например, низкоскоростных газов и жидкостей, таких как вода). Решить эти уравнения непосредственно вручную непросто, но приятно тем, что мы можем получить «точные» решения для простых задач. Использование этих уравнений для решения интересующих нас задач, скажем, при обтекании крыла воздухом или протекании воды через какую-либо систему, требует численного решения этих уравнений.

Построение числовой схемы

Чтобы решать более сложные задачи с помощью компьютера, необходим метод численного решения наших несжимаемых уравнений. Численное решение дифференциальных уравнений в частных производных или даже дифференциальных уравнений не является тривиальной задачей. Однако у наших уравнений в этом руководстве есть особая проблема (сюрприз!). То есть нам нужно решить уравнения импульса, сохраняя решение свободным от расходимости, как того требует непрерывность. Простое интегрирование по времени с помощью чего-то вроде метода Рунге-Кутты затруднено, поскольку уравнение неразрывности не имеет в себе производной по времени.

Не существует правильного или даже наилучшего метода решения уравнений, но есть много рабочих вариантов. За десятилетия было найдено несколько подходов к решению этой проблемы, таких как переформулировка с точки зрения завихренности и функции тока, введение искусственной сжимаемости и разделение операторов. Чорин (1969), а затем Ким и Мойн (1984, 1990) сформулировали очень успешный и популярный метод дробного шага, который позволит нам интегрировать уравнения при решении для поля давления напрямую, а не неявно. Метод дробного шага - это общий метод аппроксимации уравнений путем расщепления их операторов, в данном случае расщепления по давлению. Подход относительно прост и в то же время надежен, что объясняет его выбор здесь.

Во-первых, нам нужно численно дискретизировать уравнения во времени, чтобы мы могли переходить от одного момента времени к другому. Следуя Киму и Мойну (1984), мы будем использовать явный метод Адамса-Башфорта второго порядка для конвективных членов, неявный метод Кранка-Николсона второго порядка для вязких членов, простую конечную разность для производной по времени , пренебрегая градиентом давления. Эти выборы ни в коем случае не являются единственными приближениями, которые можно сделать: их выбор является частью искусства построения схемы путем управления числовым поведением схемы.

Промежуточную скорость теперь можно проинтегрировать, однако она игнорирует вклад давления и теперь расходится (несжимаемость требует, чтобы она не расходилась). Оставшаяся часть оператора необходима, чтобы перейти к следующему временному шагу.

куда - это некоторый скаляр, который нам нужно найти, что приводит к расходящейся свободной скорости. Мы можем найти приняв дивергенцию шага коррекции,

где первый член равен нулю, как того требует непрерывность, что дает уравнение Пуассона для скалярного поля, которое будет обеспечивать соленоидальную (расходящуюся свободную) скорость на следующем временном шаге.

Как показывают Ким и Мойн (1984), не совсем давление в результате расщепления оператора, но его можно найти

На этом этапе урока у нас все хорошо, мы временно разделили основные уравнения, чтобы мы могли их интегрировать. Теперь нам нужно пространственно дискретизировать операторы. Существует ряд методов, с помощью которых мы могли бы добиться этого, например, метод конечных элементов, метод конечных объемов и метод конечных разностей. В оригинальной работе Кима и Мойна (1984) они используют метод конечных разностей. Этот метод выгоден своей относительной простотой и вычислительной эффективностью, но имеет недостатки для сложной геометрии, поскольку требует структурированной сетки.

Метод конечных элементов (FEM) является удобным выбором из-за его универсальности и имеет несколько очень хороших проектов с открытым исходным кодом, помогающих в его использовании. В частности, он обрабатывает реальную геометрию в одном, двух и трех измерениях, масштабируется для очень больших задач на кластерах машин и относительно прост в использовании для элементов высокого порядка. Как правило, этот метод является более медленным из трех, однако он дает нам наибольшее преимущество при решении задач, поэтому мы будем использовать его здесь.

Даже при реализации FEM есть много вариантов. Здесь мы будем использовать МКЭ Галеркина. При этом мы приводим уравнения в форме взвешенных невязок, умножая каждое на тестовую функцию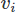 для векторов и 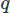для скалярного поля и интегрирования по области 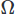. Затем мы выполняем частичное интегрирование любых производных высокого порядка, используя теорему Стокса или теорему о дивергенции. Затем мы ставим вариационную задачу, получая желаемую схему CFD.

Теперь у нас есть хорошая математическая схема в «удобной» форме для реализации, надеюсь, с некоторым пониманием того, что было необходимо для ее получения (много математики и методов блестящих исследователей, которые мы в значительной степени копируем и настраиваем).