오픈 소스 도구를 사용한 과학적 컴퓨팅 가이드

역사적으로 계산 과학은 주로 연구 과학자와 박사 후보자의 영역에 국한되었습니다. 그러나 수년에 걸쳐 – 아마도 더 큰 소프트웨어 커뮤니티에 알려지지 않은 – 우리 과학 컴퓨팅 분야의 전문가들은 대부분의 무거운 작업을 처리하는 협업 오픈 소스 라이브러리를 조용히 컴파일해 왔습니다 . 그 결과 이제 수학적 모델을 구현하는 것이 그 어느 때보다 쉬워졌으며, 이 분야는 아직 대량 소비를 위한 준비가 되지 않았지만 성공적인 구현의 기준은 크게 낮아졌습니다. 새로운 계산 코드베이스를 처음부터 개발하는 것은 일반적으로 몇 년으로 측정되는 거대한 작업이지만 이러한 오픈 소스 과학 컴퓨팅 프로젝트를 통해 이러한 계산 능력을 비교적 빠르게 활용하기 위해 액세스 가능한 예제를 실행할 수 있습니다.

과학 컴퓨팅의 목적은 자연에 존재하는 실제 시스템에 대한 과학적 통찰력을 제공하는 것이기 때문에 이 분야는 컴퓨터 소프트웨어 접근 방식을 현실로 만드는 데 있어 최첨단을 나타냅니다. 매우 높은 정확도와 해상도로 현실 세계를 모방하는 소프트웨어를 만들기 위해서는 복잡한 미분 수학이 호출되어야 하며, 대학, 국립 연구소 또는 기업 R&D 부서의 벽 너머에서는 거의 찾아볼 수 없는 지식이 필요합니다. 게다가 0과 1의 이산 언어를 사용하여 현실 세계의 연속적이고 극소량의 구조를 설명하려고 할 때 상당한 수치적 문제가 발생합니다. 계산적으로 다루기 쉽고 의미 있는 결과를 제공하는 알고리즘을 렌더링하려면 신중한 수치 변환의 철저한 노력이 필요합니다. 즉, 과학 컴퓨팅은 무거운 의무입니다.

과학 컴퓨팅을 위한 오픈 소스 도구

저는 개인적으로 FEniCS 프로젝트를 특히 좋아하여 논문 작업에 사용하며 이 자습서의 코드 예제에서 선택하는 데 있어 편견을 보여줍니다. (DUNE과 같은 다른 매우 높은 품질의 프로젝트도 사용할 수 있습니다.)

FEniCS는 "유한 요소 방법에 의한 미분 방정식의 자동화 솔루션에 특히 중점을 둔 자동화된 과학 컴퓨팅을 위한 혁신적인 개념 및 도구 개발을 위한 공동 프로젝트"라고 자칭합니다. 이것은 방대한 문제와 과학 컴퓨팅 응용 프로그램을 해결하기 위한 강력한 라이브러리입니다. 기여자는 Simula 연구소, 케임브리지 대학, 시카고 대학, 베일러 대학 및 KTH 왕립 공과 대학을 포함하며, 이들은 지난 10년 동안 집합적으로 이를 귀중한 리소스로 구축했습니다(FEniCS 코드 웜 참조).

오히려 놀라운 것은 FEniCS 라이브러리가 우리를 얼마나 많은 노력으로 보호했는지입니다. 프로젝트가 다루는 주제의 놀라운 깊이와 폭을 이해하기 위해 21장에서 비압축성 흐름을 해결하기 위한 다양한 유한 요소 계획을 비교하는 오픈 소스 교과서를 볼 수 있습니다.

이면에서 프로젝트는 우리를 위해 관심이 있거나 직접 사용할 수 있는 대규모 오픈 소스 과학 컴퓨팅 라이브러리 세트를 통합했습니다. 여기에는 특별한 순서 없이 FEniCS 프로젝트가 호출하는 프로젝트가 포함됩니다.

• PETSc: 편미분 방정식으로 모델링된 과학 응용 프로그램의 확장 가능한(병렬) 솔루션을 위한 데이터 구조 및 루틴 모음입니다.
• Trilinos 프로젝트: Sandia National Labs에서 개발한 선형 및 비선형 방정식을 풀기 위한 강력한 알고리즘 및 기술 세트입니다.
• uBLAS: "조밀하고 밀집된 희소 행렬과 선형 대수학을 위한 많은 수치 알고리즘을 위한 BLAS 레벨 1, 2, 3 기능을 제공하는 C++ 템플릿 클래스 라이브러리."
• GMP: 부호 있는 정수, 유리수 및 부동 소수점 숫자에서 작동하는 임의 정밀도 산술을 위한 무료 라이브러리입니다.
• UMFPACK: 비대칭 MultiFrontal 방법을 사용하여 비대칭 희소 선형 시스템 Ax=b를 해결하기 위한 루틴 집합입니다.
• ParMETIS: 구조화되지 않은 그래프, 메쉬를 분할하고 희소 행렬의 채우기 감소 순서를 계산하기 위한 다양한 알고리즘을 구현하는 MPI 기반 병렬 라이브러리입니다.
• NumPy: Python을 사용한 과학 컴퓨팅을 위한 기본 패키지입니다.
• CGAL: C++ 라이브러리 형태의 효율적이고 안정적인 기하학적 알고리즘.
• SCOTCH: 순차 및 병렬 그래프 분할, 정적 매핑 및 클러스터링, 순차 메시 및 하이퍼그래프 분할, 순차 및 병렬 희소 행렬 블록 순서 지정을 위한 소프트웨어 패키지 및 라이브러리입니다.
• MPI: 학계 및 산업계의 연구자 그룹이 다양한 병렬 컴퓨터에서 작동하도록 설계한 표준화되고 이식 가능한 메시지 전달 시스템입니다.
• VTK: 3D 컴퓨터 그래픽, 이미지 처리 및 시각화를 위한 무료로 사용할 수 있는 오픈 소스 소프트웨어 시스템입니다.
• SLEPc: 병렬 컴퓨터에서 대규모 희소 고유값 문제를 해결하기 위한 소프트웨어 라이브러리입니다.

프로젝트에 통합된 이 외부 패키지 목록은 상속된 기능에 대한 감각을 제공합니다. 예를 들어, MPI에 대한 통합 지원을 사용하면 컴퓨팅 클러스터 환경에서 원격 작업자 간에 확장할 수 있습니다(즉, 이 코드는 슈퍼 컴퓨터 또는 랩톱에서 실행됨).

금융 모델링, 이미지 처리, 최적화 문제, 그리고 아마도 비디오 게임 을 포함하여 이러한 프로젝트가 활용될 수 있는 과학 컴퓨팅 이외의 많은 응용 프로그램이 있다는 점도 흥미롭습니다 . 예를 들어, 이러한 오픈 소스 알고리즘 및 기술 중 일부를 사용하여 플레이어가 상호 작용할 해류/강 흐름과 같은 2차원 유체 흐름을 해결하는 비디오 게임을 만드는 것이 가능합니다(아마도 시도 및 다양한 바람과 물의 흐름으로 배를 타고 건너가십시오).

샘플 애플리케이션: 과학 컴퓨팅을 위한 오픈 소스 활용

여기에서는 이러한 오픈 소스 라이브러리 중 하나(이 경우 FEniCS 프로젝트)에서 기본적인 전산 유체 역학 체계가 어떻게 개발 및 구현되는지 보여줌으로써 수치 모델 개발과 관련된 내용을 설명하려고 합니다. FEnICS는 Python과 C++ 모두에서 API를 제공합니다. 이 예에서는 Python API를 사용합니다.

우리는 다소 기술적인 내용에 대해 논의할 것이지만 목표는 단순히 그러한 과학 컴퓨팅 코드를 개발하는 데 수반되는 것과 오늘날의 오픈 소스 도구가 우리에게 얼마나 많은 노력을 들이는지 맛보기 위한 것입니다. 그 과정에서 우리가 과학 컴퓨팅의 복잡한 세계를 이해하는 데 도움이 되기를 바랍니다. (해당 수준의 세부 사항에 관심이 있는 사람들을 위해 모든 수학적 및 과학적 토대를 자세히 설명하는 부록이 제공됩니다.)

면책 조항: 과학 컴퓨팅 소프트웨어 및 응용 프로그램에 대한 배경 지식이 거의 또는 전혀 없는 독자의 경우 이 예제의 일부가 다음과 같이 느껴질 수 있습니다.

그렇다면 절망하지 마십시오. 여기서 주요 시사점은 기존 오픈 소스 프로젝트가 이러한 많은 작업을 크게 단순화할 수 있는 정도입니다.

이를 염두에 두고 비압축성 Navier-Stokes에 대한 FEnICS 데모부터 살펴보겠습니다. 이 데모는 배관 파이프와 같은 L자형 굴곡부를 통해 흐르는 비압축성 유체의 압력과 속도를 모델링합니다.

링크된 데모 페이지의 설명은 코드를 실행하는 데 필요한 단계에 대한 훌륭하고 간결한 설정을 제공하며 관련 내용을 빠르게 살펴보기를 권장합니다. 요약하면, 데모는 비압축성 유동 방정식에 대한 굽힘을 통해 속도와 압력을 풀 것입니다. 데모는 시간이 지남에 따라 흐르는 유체의 짧은 시뮬레이션을 실행하여 결과를 애니메이션으로 만듭니다. 이것은 파이프의 공간을 나타내는 메쉬를 설정하고 유한 요소 방법을 사용하여 메쉬의 각 지점에서 속도와 압력을 수치적으로 해결함으로써 수행됩니다. 그런 다음 우리는 우리가 마음대로 사용할 수 있는 방정식을 사용하여 시간을 반복하면서 속도와 압력장을 업데이트합니다.

데모는 있는 그대로 잘 작동하지만 약간 수정하겠습니다. 데모는 Chorin split을 사용하지만, 대신 Kim과 Moin에서 영감을 받은 약간 다른 방법을 사용할 것이므로 더 안정적이기를 바랍니다. 이것은 대류 및 점성 항을 근사화하는 데 사용되는 방정식을 변경하기만 하면 되지만 그렇게 하려면 이전 시간 단계의 속도 필드를 저장하고 업데이트 방정식에 두 개의 추가 항을 추가해야 합니다. 보다 정확한 수치 근사를 위한 정보.

이 변경을 수행해 보겠습니다. 먼저 설정에 새 Function 개체를 추가합니다. 벡터나 스칼라 필드와 같은 추상적인 수학 함수를 나타내는 객체입니다. 우리는 그것을 un1 이라고 부르고 이전 속도 필드를 저장할 것입니다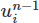 우리의 기능 공간 V .

 ... # Create functions (three distinct vector fields and a scalar field) un1 = Function(V) # the previous time step's velocity field we are adding u0 = Function(V) # the current velocity field u1 = Function(V) # the next velocity field (what's being solved for) p1 = Function(Q) # the next pressure field (what's being solved for) ...

다음으로 시뮬레이션의 각 단계에서 "임시 속도"가 업데이트되는 방식을 변경해야 합니다. 이 필드는 압력이 무시될 때 다음 시간 단계에서 대략적인 속도를 나타냅니다(이 시점에서 압력은 아직 알려지지 않음). 여기에서 초린 분할법을 보다 최근의 김과 모인 분수계단법으로 대체합니다. 즉, F1 필드의 표현식을 변경합니다.

바꾸다:

 # Tentative velocity field (a first prediction of what the next velocity field is) # for the Chorin style split # F1 = change in the velocity field + # convective term + # diffusive term - # body force term F1 = (1/k)*inner(u - u0, v)*dx + \ inner(grad(u0)*u0, v)*dx + \ nu*inner(grad(u), grad(v))*dx - \ inner(f, v)*dx

와 함께:

 # Tentative velocity field (a first prediction of what the next velocity field is) # for the Kim and Moin style split # F1 = change in the velocity field + # convective term + # diffusive term - # body force term F1 = (1/k)*inner(u - u0, v)*dx + \ (3.0/2.0) * inner(grad(u0)*u0, v)*dx - (1.0/2.0) * inner(grad(un1)*un1, v)*dx + \ (nu/2.0)*inner(grad(u+u0), grad(v))*dx - \ inner(f, v)*dx

데모에서는 이제 F1 을 사용할 때 중간 속도 필드를 해결하기 위해 업데이트된 방법을 사용합니다.

마지막으로 각 반복 단계가 끝날 때 이전 속도 필드 un1 을 업데이트하고 있는지 확인합니다.

 ... # Move to next time step un1.assign(u0) # copy the current velocity field into the previous velocity field u0.assign(u1) # copy the next velocity field into the current velocity field ...

다음은 변경 사항이 포함된 FEniCS CFD 데모의 전체 코드입니다.

 """This demo program solves the incompressible Navier-Stokes equations on an L-shaped domain using Kim and Moin's fractional step method.""" # Begin demo from dolfin import * # Print log messages only from the root process in parallel parameters["std_out_all_processes"] = False; # Load mesh from file mesh = Mesh("lshape.xml.gz") # Define function spaces (P2-P1) V = VectorFunctionSpace(mesh, "Lagrange", 2) Q = FunctionSpace(mesh, "Lagrange", 1) # Define trial and test functions u = TrialFunction(V) p = TrialFunction(Q) v = TestFunction(V) q = TestFunction(Q) # Set parameter values dt = 0.01 T = 3 nu = 0.01 # Define time-dependent pressure boundary condition p_in = Expression("sin(3.0*t)", t=0.0) # Define boundary conditions noslip = DirichletBC(V, (0, 0), "on_boundary && \ (x[0] < DOLFIN_EPS | x[1] < DOLFIN_EPS | \ (x[0] > 0.5 - DOLFIN_EPS && x[1] > 0.5 - DOLFIN_EPS))") inflow = DirichletBC(Q, p_in, "x[1] > 1.0 - DOLFIN_EPS") outflow = DirichletBC(Q, 0, "x[0] > 1.0 - DOLFIN_EPS") bcu = [noslip] bcp = [inflow, outflow] # Create functions un1 = Function(V) u0 = Function(V) u1 = Function(V) p1 = Function(Q) # Define coefficients k = Constant(dt) f = Constant((0, 0)) # Tentative velocity field (a first prediction of what the next velocity field is) # for the Kim and Moin style split # F1 = change in the velocity field + # convective term + # diffusive term - # body force term F1 = (1/k)*inner(u - u0, v)*dx + \ (3.0/2.0) * inner(grad(u0)*u0, v)*dx - (1.0/2.0) * inner(grad(un1)*un1, v)*dx + \ (nu/2.0)*inner(grad(u+u0), grad(v))*dx - \ inner(f, v)*dx a1 = lhs(F1) L1 = rhs(F1) # Pressure update a2 = inner(grad(p), grad(q))*dx L2 = -(1/k)*div(u1)*q*dx # Velocity update a3 = inner(u, v)*dx L3 = inner(u1, v)*dx - k*inner(grad(p1), v)*dx # Assemble matrices A1 = assemble(a1) A2 = assemble(a2) A3 = assemble(a3) # Use amg preconditioner if available prec = "amg" if has_krylov_solver_preconditioner("amg") else "default" # Create files for storing solution ufile = File("results/velocity.pvd") pfile = File("results/pressure.pvd") # Time-stepping t = dt while t < T + DOLFIN_EPS: # Update pressure boundary condition p_in.t = t # Compute tentative velocity step begin("Computing tentative velocity") b1 = assemble(L1) [bc.apply(A1, b1) for bc in bcu] solve(A1, u1.vector(), b1, "gmres", "default") end() # Pressure correction begin("Computing pressure correction") b2 = assemble(L2) [bc.apply(A2, b2) for bc in bcp] solve(A2, p1.vector(), b2, "cg", prec) end() # Velocity correction begin("Computing velocity correction") b3 = assemble(L3) [bc.apply(A3, b3) for bc in bcu] solve(A3, u1.vector(), b3, "gmres", "default") end() # Plot solution plot(p1, title="Pressure", rescale=True) plot(u1, title="Velocity", rescale=True) # Save to file ufile << u1 pfile << p1 # Move to next time step un1.assign(u0) u0.assign(u1) t += dt print "t =", t # Hold plot interactive()

프로그램을 실행하면 팔꿈치 주위의 흐름이 표시됩니다. 과학 컴퓨팅 코드를 직접 실행하여 애니메이션을 확인하세요! 최종 프레임의 화면은 다음과 같습니다.

시뮬레이션 종료 시 굽힘의 상대 압력, 크기에 따라 크기 조정 및 색상 지정(무차원 값):

크기(무차원 값)에 따라 크기가 조정되고 색상이 지정된 벡터 글리프로 시뮬레이션 종료 시 굽힘의 상대 속도.

그래서 우리가 한 것은 우리와 매우 유사한 체계를 구현하는 기존 데모를 가져오고 이전 시간 단계의 정보를 사용하여 더 나은 근사치를 사용하도록 수정했습니다.

이 시점에서 당신은 그것이 사소한 편집이라고 생각할 수 있습니다. 그것은 대부분 요점이었습니다. 이 오픈 소스 과학 컴퓨팅 프로젝트를 통해 4줄의 코드를 변경하여 수정된 수치 모델을 빠르게 구현할 수 있었습니다. 이러한 변경은 대규모 연구 코드에서 몇 달이 걸릴 수 있습니다.

이 프로젝트에는 시작점으로 사용할 수 있는 다른 많은 데모가 있습니다. 다양한 모델을 구현하는 프로젝트에 구축된 수많은 오픈 소스 애플리케이션도 있습니다.

결론

과학 컴퓨팅과 그 응용은 참으로 복잡합니다. 문제가 해결되지 않습니다. 그러나 많은 영역에서 점점 더 사실이 되고 있는 것처럼, 사용 가능한 오픈 소스 도구와 프로젝트의 계속 성장하는 환경은 그렇지 않으면 극도로 복잡하고 지루한 프로그래밍 작업을 상당히 단순화할 수 있습니다. 그리고 아마도 과학 컴퓨팅이 연구 커뮤니티를 넘어 쉽게 활용될 수 있을 만큼 충분히 접근할 수 있는 시대가 가까웠습니다.

부록: 과학 및 수학 기반

관심 있는 분들을 위해 위의 전산 유체 역학 가이드의 기술적 토대가 있습니다. 다음 내용은 일반적으로 12개 정도의 대학원 수준 과정에서 다루는 주제에 대한 매우 유용하고 간결한 요약 역할을 합니다. 주제에 대한 깊은 이해에 관심이 있는 대학원생 및 수학적 유형은 이 자료가 상당히 매력적일 수 있습니다.

유체 역학

일반적으로 "모델링"은 급수 근사를 사용하여 실제 시스템을 해결하는 프로세스입니다. 모델은 종종 컴퓨터 구현에 부적합한 연속 방정식을 포함하므로 수치적 방법으로 더 근사해야 합니다.

유체 역학의 경우 기본 방정식인 Navier-Stokes 방정식에서 이 가이드를 시작하고 이를 CFD 체계를 개발하는 데 사용하겠습니다.

Navier-Stokes 방정식은 유체 흐름을 매우 잘 설명하는 일련의 편미분 방정식(PDE)이므로 시작점이 됩니다. 그들은 레이놀즈 수송 정리를 통해 던져진 질량, 운동량 및 에너지 보존 법칙과 가우스의 정리를 적용하고 스토크의 가설을 불러일으키는 법칙에서 파생될 수 있습니다. 방정식은 온도, 밀도 및 속도 의미와 같은 통계적 특성을 제공하기에 충분한 유체 입자가 있다고 가정하는 연속체 가정이 필요합니다. 또한 표면 응력 텐서와 변형률 텐서 간의 선형 관계, 응력 텐서의 대칭 및 등방성 유체 가정이 필요합니다. 결과 코드의 적용 가능성을 평가할 수 있도록 이 개발 중에 만들고 상속한 가정을 아는 것이 중요합니다. 더 이상 고민하지 않고 아인슈타인 표기법의 나비에-스토크스 방정식:

질량 보존:

운동량 보존:

에너지 보존:

여기서 편차 응력은 다음과 같습니다.

물리적 세계에서 대부분의 유체 흐름을 지배하는 매우 일반적이지만 직접적으로 많이 사용되지는 않습니다. 방정식에 대한 알려진 정확한 솔루션은 상대적으로 거의 없으며 존재와 부드러움 문제를 해결할 수 있는 사람에게 $1,000,000 밀레니엄 상이 있습니다. 중요한 부분은 복잡성을 줄이기 위한 일련의 가정을 통해 모델 개발을 위한 출발점이 있다는 것입니다(고전 물리학에서 가장 어려운 방정식 중 일부임).

일을 "단순하게" 유지하기 위해 우리는 영역별 지식을 사용하여 유체에 대한 비압축성 가정을 만들고 열 방정식이 되는 에너지 보존 방정식이 필요하지 않도록 일정한 온도를 가정합니다(분리). 이제 우리는 여전히 PDE이지만 많은 실제 유체 문제를 해결하면서 훨씬 더 간단한 두 개의 방정식을 가지고 있습니다.

연속 방정식

운동량 방정식

이 시점에서 우리는 이제 비압축성 유체 흐름(예: 물과 같은 저속 기체 및 액체)에 대한 멋진 수학적 모델을 갖게 되었습니다. 이 방정식을 직접 손으로 푸는 것은 쉽지 않지만 간단한 문제에 대해 "정확한" 해를 얻을 수 있다는 점에서 좋습니다. 날개 위로 흐르는 공기 또는 일부 시스템을 통해 흐르는 물과 같이 관심 있는 문제를 해결하기 위해 이러한 방정식을 사용하려면 이러한 방정식을 수치적으로 풀어야 합니다.

수치 체계 만들기

컴퓨터를 사용하여 더 복잡한 문제를 풀기 위해서는 우리의 비압축 방정식을 수치적으로 푸는 방법이 필요합니다. 편미분 방정식 또는 미분 방정식을 수치적으로 푸는 것은 쉬운 일이 아닙니다. 그러나 이 가이드의 방정식에는 특별한 문제가 있습니다(놀랍습니다!). 즉, 연속성에 의해 요구되는 대로 솔루션 발산을 자유롭게 유지하면서 운동량 방정식을 풀어야 합니다. Runge-Kutta 방법과 같은 것을 통한 간단한 시간 적분은 연속 방정식에 시간 도함수가 없기 때문에 어렵습니다.

방정식을 푸는 데 정확하거나 가장 좋은 방법은 없지만 실행 가능한 옵션은 많이 있습니다. 수십 년 동안 와도 및 흐름 기능 측면에서 재구성, 인공 압축성 도입, 연산자 분할과 같은 문제를 해결하기 위한 여러 접근 방식이 발견되었습니다. Chorin(1969), 그리고 Kim and Moin(1984, 1990)은 매우 성공적이고 대중적인 분수 단계 방법을 공식화하여 방정식을 적분하면서 압력장을 암묵적으로 풀기보다는 직접 풀 수 있게 해줍니다. 분수 단계 방법은 연산자를 분할하여 방정식을 근사하는 일반적인 방법입니다. 이 경우에는 압력을 따라 분할합니다. 접근 방식은 상대적으로 간단하지만 강력하여 여기에서 선택하도록 동기를 부여합니다.

첫째, 한 시점에서 다음 시점으로 이동할 수 있도록 방정식을 수치적으로 구분해야 합니다. Kim and Moin(1984)에 따르면 대류 항에 대해서는 2차 명시적 Adams-Bashforth 방법을, 점성 항에는 2차 암시적 Crank-Nicholson 방법을, 시간 도함수에 대해서는 단순 유한 차분을 사용할 것입니다. , 압력 구배는 무시합니다. 이러한 선택이 결코 유일한 근사치는 아닙니다. 선택은 체계의 수치적 동작을 제어하여 체계를 구축하는 기술의 일부입니다.

이제 중간 속도를 통합할 수 있지만 압력의 기여를 무시하고 이제 발산합니다(비압축성으로 인해 발산이 없어야 함). 나머지 연산자는 다음 단계로 이동하는 데 필요합니다.

어디 는 발산 자유 속도를 초래하는 결과를 찾아야 하는 일부 스칼라입니다. 우리는 찾을 수있어 수정 단계의 발산을 취함으로써,

여기서 첫 번째 항은 연속성에 의해 요구되는 0이며 다음 시간 단계에서 솔레노이드(발산 없는) 속도를 제공할 스칼라 필드에 대한 푸아송 방정식을 생성합니다.

Kim and Moin(1984)이 보여주듯이, 연산자 분할의 결과로 정확히 압력은 아니지만 다음으로 찾을 수 있습니다.

튜토리얼의 이 시점에서 우리는 꽤 잘하고 있습니다. 우리는 지배 방정식을 통합할 수 있도록 일시적으로 이산화했습니다. 이제 연산자를 공간적으로 구분해야 합니다. 이를 수행할 수 있는 여러 가지 방법, 예를 들어 유한 요소 방법, 유한 체적 방법 및 유한 차분 방법이 있습니다. Kim and Moin(1984)의 원작에서는 유한차분법으로 진행한다. 이 방법은 상대적 단순성과 계산 효율성에 유리하지만 구조화된 메쉬가 필요하기 때문에 복잡한 형상에는 어려움을 겪습니다.

FEM(Finite Element Method)은 일반성을 위한 편리한 선택이며 사용에 도움이 되는 매우 훌륭한 오픈 소스 프로젝트가 있습니다. 특히 1차원, 2차원 및 3차원에서 실제 형상을 처리하고 기계 클러스터의 매우 큰 문제에 대해 확장되며 고차 요소에 대해 사용하기가 상대적으로 쉽습니다. 일반적으로 이 방법은 세 가지 방법 중 더 느리지만 문제 전체에서 가장 많은 마일리지를 제공하므로 여기에서 사용합니다.

FEM을 구현할 때도 많은 선택이 있습니다. 여기서는 Galerkin FEM을 사용합니다. 그렇게 함으로써 우리는 각각에 테스트 함수를 곱하여 가중 잔차 형식으로 방정식을 캐스팅합니다.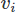 벡터 및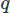 스칼라 필드의 경우 도메인에 대한 통합 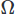. 그런 다음 Stoke의 정리 또는 발산 정리를 사용하여 고차 도함수에 대해 부분 적분을 수행합니다. 그런 다음 원하는 CFD 방식을 산출하는 변형 문제를 제기합니다.

우리는 이제 구현을 위한 "편리한" 형태의 멋진 수학적 계획을 갖게 되었고, 거기에 도달하는 데 필요한 것이 무엇인지 알 수 있게 되었습니다(많은 수학과 우리가 거의 복사하고 조정하는 뛰어난 연구원의 방법).