Una guía para la computación científica con herramientas de código abierto

Históricamente, la ciencia computacional se ha limitado en gran medida al ámbito de los científicos investigadores y los doctorandos. Sin embargo, a lo largo de los años, quizás sin el conocimiento de la comunidad de software en general, los intelectuales de la computación científica hemos estado compilando silenciosamente bibliotecas colaborativas de código abierto que manejan la gran mayoría del trabajo pesado . El resultado es que ahora es más fácil que nunca implementar modelos matemáticos y, aunque es posible que el campo aún no esté listo para el consumo masivo, el listón para una implementación exitosa se ha reducido drásticamente. Desarrollar una nueva base de código computacional desde cero es una tarea enorme, normalmente medida en años, pero estos proyectos de computación científica de código abierto hacen posible que se ejecuten con ejemplos accesibles para aprovechar estas capacidades computacionales con relativa rapidez.

Dado que el propósito de la computación científica es proporcionar una visión científica de los sistemas reales que existen en la naturaleza, la disciplina representa la vanguardia en hacer que el software de computadora se acerque a la realidad. Para crear un software que imite el mundo real con un alto grado de precisión y resolución, se deben invocar matemáticas diferenciales complejas, lo que requiere un conocimiento que rara vez se encuentra más allá de las paredes de las universidades, los laboratorios nacionales o los departamentos corporativos de I+D. Además de esto, se presentan importantes desafíos numéricos cuando se intenta describir el tejido infinitesimal continuo del mundo real utilizando el lenguaje discreto de ceros y unos. Es necesario un esfuerzo exhaustivo de transformación numérica cuidadosa para generar algoritmos que sean manejables computacionalmente y que brinden resultados significativos. En otras palabras, la computación científica es un trabajo pesado.

Herramientas de código abierto para computación científica

Personalmente, me gusta especialmente el proyecto FEniCS, lo uso para mi trabajo de tesis y demostraré mi preferencia al seleccionarlo para nuestro ejemplo de código para este tutorial. (Hay otros proyectos de muy alta calidad, como DUNE, que también se podrían usar).

FEniCS se describe a sí mismo como "un proyecto colaborativo para el desarrollo de conceptos y herramientas innovadores para la computación científica automatizada, con un enfoque particular en la solución automatizada de ecuaciones diferenciales mediante métodos de elementos finitos". Esta es una biblioteca poderosa para resolver una gran variedad de problemas y aplicaciones informáticas científicas. Sus colaboradores incluyen el Laboratorio de Investigación Simula, la Universidad de Cambridge, la Universidad de Chicago, la Universidad de Baylor y el Instituto Real de Tecnología KTH, quienes colectivamente lo han convertido en un recurso invaluable en el transcurso de la última década (ver los códigos FEniCS).

Lo que es bastante sorprendente es cuánto esfuerzo nos ha protegido la biblioteca FEniCS. Para tener una idea de la asombrosa profundidad y amplitud de los temas que cubre el proyecto, uno puede ver su libro de texto de código abierto, donde el Capítulo 21 incluso compara varios esquemas de elementos finitos para resolver flujos incompresibles.

Detrás de escena, el proyecto ha integrado para nosotros un gran conjunto de bibliotecas de computación científica de código abierto, que pueden ser de interés o de uso directo. Estos incluyen, sin ningún orden en particular, los proyectos que el proyecto FEniCS llama:

• PETSc: un conjunto de estructuras de datos y rutinas para la solución escalable (paralela) de aplicaciones científicas modeladas por ecuaciones diferenciales parciales.
• Proyecto Trilinos: un conjunto de algoritmos y tecnologías robustos para resolver ecuaciones lineales y no lineales, desarrollado a partir del trabajo en Sandia National Labs.
• uBLAS: "Una biblioteca de clases de plantillas de C++ que proporciona funcionalidad BLAS de nivel 1, 2, 3 para matrices densas, empaquetadas y dispersas y muchos algoritmos numéricos para álgebra lineal".
• GMP: una biblioteca gratuita para aritmética de precisión arbitraria, que opera con números enteros con signo, números racionales y números de punto flotante.
• UMFPACK: Un conjunto de rutinas para resolver sistemas lineales dispersos asimétricos, Ax=b, usando el método MultiFrontal Asimétrico.
• ParMETIS: una biblioteca paralela basada en MPI que implementa una variedad de algoritmos para particionar gráficos no estructurados, mallas y para calcular órdenes de reducción de relleno de matrices dispersas.
• NumPy: El paquete fundamental para la computación científica con Python.
• CGAL: Algoritmos geométricos eficientes y fiables en forma de biblioteca C++.
• SCOTCH: un paquete de software y bibliotecas para el particionamiento de gráficos paralelos y secuenciales, el mapeo y la agrupación estáticos, el particionamiento hipergráfico y de malla secuencial, y el ordenamiento de bloques de matriz dispersa secuencial y paralelo.
• MPI: Un sistema de paso de mensajes estandarizado y portátil diseñado por un grupo de investigadores de la academia y la industria para funcionar en una amplia variedad de computadoras paralelas.
• VTK: un sistema de software de código abierto y disponible gratuitamente para gráficos 3D por computadora, procesamiento de imágenes y visualización.
• SLEPc: una biblioteca de software para la solución de problemas de valores propios dispersos a gran escala en computadoras paralelas.

Esta lista de paquetes externos integrados en el proyecto nos da una idea de sus capacidades heredadas. Por ejemplo, tener soporte integrado para MPI permite escalar entre trabajadores remotos en un entorno de clúster de cómputo (es decir, este código se ejecutará en una supercomputadora o en su computadora portátil).

También es interesante notar que existen muchas aplicaciones más allá de la computación científica para las cuales estos proyectos podrían utilizarse, incluidos el modelado financiero, el procesamiento de imágenes, los problemas de optimización y quizás incluso los videojuegos. Sería posible, por ejemplo, crear un videojuego que utilice algunos de estos algoritmos y técnicas de código abierto para resolver el flujo de un fluido bidimensional, como el de las corrientes oceánicas o fluviales con las que un jugador interactuaría (quizás intente y navegar un barco con diferentes flujos de viento y agua).

Una aplicación de muestra: aprovechar el código abierto para la computación científica

Aquí intentaré dar una idea de lo que implica desarrollar un modelo numérico mostrando cómo se desarrolla e implementa un esquema básico de dinámica de fluidos computacional en una de estas bibliotecas de código abierto, en este caso el proyecto FEniCS. FEnICS proporciona API tanto en Python como en C++. Para este ejemplo, usaremos su API de Python.

Discutiremos algunos contenidos bastante técnicos, pero el objetivo será simplemente dar una idea de lo que implica el desarrollo de un código de computación científica y cuánto trabajo de campo hacen las herramientas de código abierto de hoy en día por nosotros. En el proceso, esperamos ayudar a desmitificar el complejo mundo de la computación científica. (Tenga en cuenta que se proporciona un Apéndice que detalla todos los fundamentos matemáticos y científicos para aquellos que estén interesados ​​en ese nivel de detalle).

DESCARGO DE RESPONSABILIDAD: Para aquellos lectores con poca o ninguna experiencia en software y aplicaciones informáticas científicas, partes de este ejemplo pueden hacerles sentir así:

Si es así, no se desespere. La conclusión principal aquí es hasta qué punto los proyectos de código abierto existentes pueden simplificar en gran medida muchas de estas tareas.

Con eso en mente, comencemos mirando la demostración de FEnICS para Navier-Stokes incompresible. Esta demostración modela la presión y la velocidad de un fluido incompresible que fluye a través de un codo en forma de L, como una tubería de plomería.

La descripción en la página de demostración vinculada brinda una configuración excelente y concisa de los pasos necesarios para ejecutar el código, y lo animo a que eche un vistazo rápido para ver qué implica. Para resumir, la demostración resolverá la velocidad y la presión a través de la curva para las ecuaciones de flujo incompresible. La demostración ejecuta una breve simulación del fluido que fluye con el tiempo, animando los resultados a medida que avanza. Esto se logra configurando la malla que representa el espacio en la tubería y utilizando el método de elementos finitos para resolver numéricamente la velocidad y la presión en cada punto de la malla. Luego iteramos a través del tiempo, actualizando los campos de velocidad y presión a medida que avanzamos, nuevamente usando las ecuaciones que tenemos a nuestra disposición.

La demostración funciona bien tal como está, pero vamos a modificarla ligeramente. La demostración usa la división de Chorin, pero en su lugar vamos a usar un método ligeramente diferente inspirado en Kim y Moin, que esperamos sea más estable. Esto solo requiere que cambiemos la ecuación utilizada para aproximar los términos convectivo y viscoso, pero para hacerlo necesitamos almacenar el campo de velocidad del paso de tiempo anterior y agregar dos términos adicionales a la ecuación de actualización, que usará ese anterior. información para una aproximación numérica más precisa.

Así que hagamos este cambio. Primero, agregamos un nuevo objeto Function a la configuración. Este es un objeto que representa una función matemática abstracta, como un campo vectorial o escalar. Lo llamaremos un1 , almacenará el campo de velocidad anterior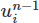 en nuestro espacio funcional V .

 ... # Create functions (three distinct vector fields and a scalar field) un1 = Function(V) # the previous time step's velocity field we are adding u0 = Function(V) # the current velocity field u1 = Function(V) # the next velocity field (what's being solved for) p1 = Function(Q) # the next pressure field (what's being solved for) ...

A continuación, debemos cambiar la forma en que se actualiza la "velocidad tentativa" durante cada paso de la simulación. Este campo representa la velocidad aproximada en el siguiente paso de tiempo cuando se ignora la presión (en este punto aún no se conoce la presión). Aquí es donde reemplazamos el método de división de Chorin con el método de pasos fraccionarios más reciente de Kim y Moin. En otras palabras, cambiaremos la expresión del campo F1 :

Reemplazar:

 # Tentative velocity field (a first prediction of what the next velocity field is) # for the Chorin style split # F1 = change in the velocity field + # convective term + # diffusive term - # body force term F1 = (1/k)*inner(u - u0, v)*dx + \ inner(grad(u0)*u0, v)*dx + \ nu*inner(grad(u), grad(v))*dx - \ inner(f, v)*dx

Con:

 # Tentative velocity field (a first prediction of what the next velocity field is) # for the Kim and Moin style split # F1 = change in the velocity field + # convective term + # diffusive term - # body force term F1 = (1/k)*inner(u - u0, v)*dx + \ (3.0/2.0) * inner(grad(u0)*u0, v)*dx - (1.0/2.0) * inner(grad(un1)*un1, v)*dx + \ (nu/2.0)*inner(grad(u+u0), grad(v))*dx - \ inner(f, v)*dx

de modo que la demostración ahora usa nuestro método actualizado para resolver el campo de velocidad intermedia cuando usa F1 .

Finalmente, asegúrese de que estamos actualizando el campo de velocidad anterior, un1 , al final de cada paso de iteración

 ... # Move to next time step un1.assign(u0) # copy the current velocity field into the previous velocity field u0.assign(u1) # copy the next velocity field into the current velocity field ...

De modo que el siguiente es el código completo de nuestra demostración FEniCS CFD, con nuestros cambios incluidos:

 """This demo program solves the incompressible Navier-Stokes equations on an L-shaped domain using Kim and Moin's fractional step method.""" # Begin demo from dolfin import * # Print log messages only from the root process in parallel parameters["std_out_all_processes"] = False; # Load mesh from file mesh = Mesh("lshape.xml.gz") # Define function spaces (P2-P1) V = VectorFunctionSpace(mesh, "Lagrange", 2) Q = FunctionSpace(mesh, "Lagrange", 1) # Define trial and test functions u = TrialFunction(V) p = TrialFunction(Q) v = TestFunction(V) q = TestFunction(Q) # Set parameter values dt = 0.01 T = 3 nu = 0.01 # Define time-dependent pressure boundary condition p_in = Expression("sin(3.0*t)", t=0.0) # Define boundary conditions noslip = DirichletBC(V, (0, 0), "on_boundary && \ (x[0] < DOLFIN_EPS | x[1] < DOLFIN_EPS | \ (x[0] > 0.5 - DOLFIN_EPS && x[1] > 0.5 - DOLFIN_EPS))") inflow = DirichletBC(Q, p_in, "x[1] > 1.0 - DOLFIN_EPS") outflow = DirichletBC(Q, 0, "x[0] > 1.0 - DOLFIN_EPS") bcu = [noslip] bcp = [inflow, outflow] # Create functions un1 = Function(V) u0 = Function(V) u1 = Function(V) p1 = Function(Q) # Define coefficients k = Constant(dt) f = Constant((0, 0)) # Tentative velocity field (a first prediction of what the next velocity field is) # for the Kim and Moin style split # F1 = change in the velocity field + # convective term + # diffusive term - # body force term F1 = (1/k)*inner(u - u0, v)*dx + \ (3.0/2.0) * inner(grad(u0)*u0, v)*dx - (1.0/2.0) * inner(grad(un1)*un1, v)*dx + \ (nu/2.0)*inner(grad(u+u0), grad(v))*dx - \ inner(f, v)*dx a1 = lhs(F1) L1 = rhs(F1) # Pressure update a2 = inner(grad(p), grad(q))*dx L2 = -(1/k)*div(u1)*q*dx # Velocity update a3 = inner(u, v)*dx L3 = inner(u1, v)*dx - k*inner(grad(p1), v)*dx # Assemble matrices A1 = assemble(a1) A2 = assemble(a2) A3 = assemble(a3) # Use amg preconditioner if available prec = "amg" if has_krylov_solver_preconditioner("amg") else "default" # Create files for storing solution ufile = File("results/velocity.pvd") pfile = File("results/pressure.pvd") # Time-stepping t = dt while t < T + DOLFIN_EPS: # Update pressure boundary condition p_in.t = t # Compute tentative velocity step begin("Computing tentative velocity") b1 = assemble(L1) [bc.apply(A1, b1) for bc in bcu] solve(A1, u1.vector(), b1, "gmres", "default") end() # Pressure correction begin("Computing pressure correction") b2 = assemble(L2) [bc.apply(A2, b2) for bc in bcp] solve(A2, p1.vector(), b2, "cg", prec) end() # Velocity correction begin("Computing velocity correction") b3 = assemble(L3) [bc.apply(A3, b3) for bc in bcu] solve(A3, u1.vector(), b3, "gmres", "default") end() # Plot solution plot(p1, title="Pressure", rescale=True) plot(u1, title="Velocity", rescale=True) # Save to file ufile << u1 pfile << p1 # Move to next time step un1.assign(u0) u0.assign(u1) t += dt print "t =", t # Hold plot interactive()

Ejecutar el programa muestra el flujo alrededor del codo. ¡Ejecute el código informático científico usted mismo para verlo animado! Las pantallas del cuadro final se presentan a continuación.

Presiones relativas en el pliegue al final de la simulación, escaladas y coloreadas por magnitud (valores adimensionales):

Velocidades relativas en la curva al final de la simulación como glifos vectoriales escalados y coloreados por magnitud (valores no dimensionales).

Entonces, lo que hemos hecho es tomar una demostración existente, que implementa un esquema muy similar al nuestro con bastante facilidad, y lo modificamos para usar mejores aproximaciones utilizando información del paso de tiempo anterior.

En este punto, podrías estar pensando que fue una edición trivial. Lo fue, y ese es en gran medida el punto. Este proyecto de computación científica de código abierto nos ha permitido implementar rápidamente un modelo numérico modificado cambiando cuatro líneas de código. Dichos cambios pueden llevar meses en códigos de investigación grandes.

El proyecto tiene muchas otras demostraciones que podrían usarse como punto de partida. Incluso hay una serie de aplicaciones de código abierto creadas en el proyecto que implementan varios modelos.

Conclusión

La computación científica y sus aplicaciones son ciertamente complejas. No hay forma de evitar eso. Pero como es cada vez más cierto en tantos dominios, el panorama cada vez mayor de herramientas y proyectos de código abierto disponibles puede simplificar significativamente lo que de otro modo serían tareas de programación extremadamente complicadas y tediosas. Y tal vez esté cerca el momento en que la computación científica se vuelva lo suficientemente accesible como para ser fácilmente utilizada más allá de la comunidad investigadora.

APÉNDICE: Bases científicas y matemáticas

Para aquellos interesados, aquí están los fundamentos técnicos de nuestra guía de dinámica de fluidos computacional anterior. Lo que sigue servirá como un resumen muy útil y conciso de los temas que normalmente se cubren en el transcurso de una docena de cursos de posgrado. Los estudiantes de posgrado y los tipos matemáticos interesados ​​en una comprensión profunda del tema pueden encontrar este material bastante interesante.

Mecánica de fluidos

“Modelado”, en general, es el proceso de resolver algún sistema real con una serie de aproximaciones. El modelo, a menudo implicará ecuaciones continuas inadecuadas para la implementación de la computadora, por lo que debe aproximarse aún más con métodos numéricos.

Para la mecánica de fluidos, comencemos esta guía con las ecuaciones fundamentales, las ecuaciones de Navier-Stokes, y usémoslas para desarrollar un esquema CFD.

Las ecuaciones de Navier-Stokes son una serie de ecuaciones diferenciales parciales (PDEs) que describen muy bien los flujos de fluidos y, por lo tanto, son nuestro punto de partida. Se pueden derivar de las leyes de conservación de la masa, el momento y la energía arrojadas a través de un teorema de transporte de Reynolds y aplicando el teorema de Gauss e invocando la hipótesis de Stoke. Las ecuaciones requieren una suposición continua, donde se supone que tenemos suficientes partículas de fluido para dar significado a propiedades estadísticas como la temperatura, la densidad y la velocidad. Además, se necesita una relación lineal entre el tensor de tensión superficial y el tensor de velocidad de deformación, simetría en el tensor de tensión y supuestos de fluido isotrópico. Es importante conocer las suposiciones que hacemos y heredamos durante este desarrollo para que podamos evaluar la aplicabilidad en el código resultante. Las ecuaciones de Navier-Stokes en notación de Einstein, sin más preámbulos:

Conservación de la masa:

Conservación de momento:

Conservacion de energia:

donde el esfuerzo desviador es:

Si bien son muy generales y rigen la mayoría de los flujos de fluidos en el mundo físico, no son de mucha utilidad directamente. Hay relativamente pocas soluciones exactas conocidas para las ecuaciones, y hay un Premio del Milenio de $ 1,000,000 para cualquiera que pueda resolver el problema de la existencia y la suavidad. La parte importante es que tenemos un punto de partida para el desarrollo de nuestro modelo haciendo una serie de suposiciones para reducir la complejidad (son algunas de las ecuaciones más difíciles de la física clásica).

Para mantener las cosas "simples", utilizaremos nuestro conocimiento específico del dominio para hacer una suposición incompresible sobre el fluido y asumir temperaturas constantes de modo que la ecuación de conservación de la energía, que se convierte en la ecuación del calor, no sea necesaria (desacoplada). Ahora tenemos dos ecuaciones, todavía PDE, pero significativamente más sencillas y que aún resuelven una gran cantidad de problemas de fluidos reales.

Ecuación de continuidad

Ecuaciones de momento

En este punto, ahora tenemos un buen modelo matemático para flujos de fluidos incompresibles (gases de baja velocidad y líquidos como el agua, por ejemplo). Resolver estas ecuaciones directamente a mano no es fácil, pero es bueno porque podemos obtener soluciones "exactas" para problemas simples. El uso de estas ecuaciones para abordar problemas de interés, por ejemplo, el aire que fluye sobre un ala o el agua que fluye a través de algún sistema, requiere que resolvamos estas ecuaciones numéricamente.

Construcción de un esquema numérico

Para resolver problemas más complejos usando la computadora, se necesita un método para resolver numéricamente nuestras ecuaciones incompresibles. Resolver ecuaciones diferenciales parciales, o incluso ecuaciones diferenciales, numéricamente no es trivial. Sin embargo, nuestras ecuaciones en esta guía tienen un desafío particular (¡sorpresa!). Es decir, necesitamos resolver las ecuaciones de momento mientras mantenemos la solución libre de divergencia, como lo requiere la continuidad. Una integración de tiempo simple a través de algo como el método de Runge-Kutta se hace difícil ya que la ecuación de continuidad no tiene una derivada de tiempo dentro de ella.

No existe un método correcto, o incluso el mejor, para resolver las ecuaciones, pero hay muchas opciones viables. A lo largo de las décadas, se han encontrado varios enfoques para abordar el problema, como la reformulación en términos de vorticidad y la función de flujo, la introducción de compresibilidad artificial y la división de operadores. Chorin (1969), y luego Kim y Moin (1984, 1990), formularon un método de pasos fraccionarios muy exitoso y popular que nos permitirá integrar las ecuaciones mientras resolvemos el campo de presión directamente, en lugar de implícitamente. El método de pasos fraccionarios es un método general para aproximar ecuaciones dividiendo sus operadores, en este caso dividiendo a lo largo de la presión. El enfoque es relativamente simple y, sin embargo, robusto, lo que motiva su elección aquí.

Primero, necesitamos diferenciar numéricamente las ecuaciones en el tiempo para que podamos pasar de un punto en el tiempo al siguiente. Siguiendo a Kim y Moin (1984), utilizaremos el método Adams-Bashforth explícito de segundo orden para los términos convectivos, el método Crank-Nicholson implícito de segundo orden para los términos viscosos, una diferencia finita simple para la derivada temporal , despreciando el gradiente de presión. Estas elecciones no son de ninguna manera las únicas aproximaciones que se pueden hacer: su selección es parte del arte en la construcción del esquema controlando el comportamiento numérico del esquema.

La velocidad intermedia ahora se puede integrar, sin embargo, ignora la contribución de la presión y ahora es divergente (la incompresibilidad requiere que esté libre de divergencias). Se necesita el resto del operador para llevarnos al siguiente paso de tiempo.

donde es algún escalar que necesitamos para encontrar que da como resultado una velocidad libre divergente. Podemos encontrar tomando la divergencia del paso de corrección,

donde el primer término es cero como lo requiere la continuidad, produciendo una ecuación de Poisson para un campo escalar que proporcionará una velocidad solenoidal (libre de divergencias) en el siguiente paso de tiempo.

Como muestran Kim y Moin (1984), no es exactamente la presión como resultado de la división del operador, pero se puede encontrar por

En este punto del tutorial lo estamos haciendo bastante bien, hemos discritizado temporalmente las ecuaciones gobernantes para que podamos integrarlas. Ahora necesitamos diferenciar espacialmente a los operadores. Existen varios métodos con los que podemos lograr esto, por ejemplo, el método de los elementos finitos, el método del volumen finito y el método de las diferencias finitas. En el trabajo original de Kim y Moin (1984), proceden con el método de diferencias finitas. El método es ventajoso por su relativa simplicidad y eficiencia computacional, pero sufre por geometrías complejas ya que requiere una malla estructurada.

El método de elementos finitos (FEM) es una selección conveniente por su generalidad y tiene algunos proyectos de código abierto muy buenos que ayudan en su uso. En particular, maneja geometrías reales en una, dos y tres dimensiones, escala para problemas muy grandes en grupos de máquinas y es relativamente fácil de usar para elementos de alto orden. Por lo general, el método es el más lento de los tres, sin embargo, nos dará el mayor recorrido en los problemas, por lo que lo usaremos aquí.

Incluso cuando se implementa el FEM hay muchas opciones. Aquí usaremos el Galerkin FEM. Al hacerlo, expresamos las ecuaciones en forma residual ponderada multiplicando cada una por una función de prueba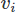 para los vectores y 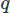para el campo escalar, e integrando sobre el dominio 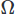. Luego realizamos una integración parcial en cualquier derivada de alto orden utilizando el teorema de Stoke o el teorema de la divergencia. Luego planteamos el problema variacional, produciendo nuestro esquema CFD deseado.

Ahora tenemos un buen esquema matemático en una forma "conveniente" para la implementación, con suerte con algún sentido de lo que se necesitaba para llegar allí (muchas matemáticas y métodos de investigadores brillantes que copiamos y modificamos).