Un ghid pentru calculul științific cu instrumente open source

Din punct de vedere istoric, știința computațională a fost în mare parte limitată la domeniul cercetătorilor de știință și al candidaților la doctorat. Cu toate acestea, de-a lungul anilor – poate fără să știe comunitatea mai mare de software – noi, capete de calcul științific, au compilat în liniște biblioteci colaborative open-source care se ocupă de marea majoritate a sarcinilor grele . Rezultatul este că acum este mai ușor ca niciodată să implementați modele matematice și, deși domeniul poate să nu fie încă pregătit pentru consum în masă, bara pentru implementarea cu succes a fost drastic coborâtă. Dezvoltarea unei noi baze de coduri computaționale de la zero este o întreprindere uriașă, măsurată de obicei în ani, dar aceste proiecte de calcul științific open source fac posibilă rularea cu exemple accesibile pentru a valorifica relativ rapid aceste abilități de calcul.

Întrucât scopul calculului științific este de a oferi o perspectivă științifică asupra sistemelor reale care există în natură, disciplina reprezintă vârful de ultimă oră în transformarea software-ului în realitate. Pentru a realiza un software care imită lumea reală la un grad foarte înalt de precizie și rezoluție, trebuie invocată matematica diferențială complexă, care necesită cunoștințe care se găsesc rar dincolo de zidurile universităților, laboratoarelor naționale sau departamentelor de cercetare și dezvoltare corporative. În plus, provocări numerice semnificative apar atunci când încearcă să descrie țesătura continuă, infinitezimală a lumii reale, folosind limbajul discret al zerourilor și al unuurilor. Un efort exhaustiv de transformare numerică atentă este necesar pentru a reda algoritmi care sunt atât tratabili din punct de vedere computațional, cât și care oferă rezultate semnificative. Cu alte cuvinte, informatica științifică este grea.

Instrumente open source pentru calcul științific

Personal îmi place în mod deosebit proiectul FEniCS, folosindu-l pentru lucrarea mea de teză și îmi voi demonstra părtinirea în selectarea acestuia pentru exemplul nostru de cod pentru acest tutorial. (Există și alte proiecte de foarte înaltă calitate, cum ar fi DUNE, pe care le-ar putea folosi, de asemenea.)

FEniCS este auto-descris ca „un proiect de colaborare pentru dezvoltarea de concepte și instrumente inovatoare pentru calculul științific automatizat, cu un accent deosebit pe soluția automată a ecuațiilor diferențiale prin metode cu elemente finite”. Aceasta este o bibliotecă puternică pentru rezolvarea unei game uriașe de probleme și aplicații de calcul științific. Printre contribuatorii săi se numără Laboratorul de Cercetare Simula, Universitatea Cambridge, Universitatea din Chicago, Universitatea Baylor și Institutul Regal de Tehnologie KTH, care au transformat-o împreună într-o resursă de neprețuit pe parcursul ultimului deceniu (vezi FEniCS codeswarm).

Ceea ce este mai degrabă uimitor este cât de mult efort ne-a protejat biblioteca FEniCS. Pentru a avea o idee uimitoarea profunzime și amploare a subiectelor pe care le acoperă proiectul, puteți vizualiza manualul de text cu sursă deschisă, unde Capitolul 21 chiar compară diverse scheme de elemente finite pentru rezolvarea fluxurilor incompresibile.

În culise, proiectul a integrat pentru noi un set mare de biblioteci de calcul științific open source, care pot fi de interes sau de utilizare directă. Acestea includ, fără o ordine anume, proiectele pe care proiectul FEniCS le evocă:

• PETSc: O suită de structuri de date și rutine pentru soluția scalabilă (paralelă) a aplicațiilor științifice modelate prin ecuații cu diferențe parțiale.
• Proiectul Trilinos: Un set de algoritmi și tehnologii robuste pentru rezolvarea ecuațiilor liniare și neliniare, dezvoltate din munca de la Sandia National Labs.
• uBLAS: „O bibliotecă de clasă de șabloane C++ care oferă funcționalitate BLAS de nivel 1, 2, 3 pentru matrici dense, împachetate și rare și mulți algoritmi numerici pentru algebra liniară.”
• GMP: O bibliotecă gratuită pentru aritmetică de precizie arbitrară, care operează pe numere întregi cu semn, numere raționale și numere în virgulă mobilă.
• UMFPACK: Un set de rutine pentru rezolvarea sistemelor liniare rare și asimetrice, Ax=b, folosind metoda MultiFrontal asimetrică.
• ParMETIS: O bibliotecă paralelă bazată pe MPI care implementează o varietate de algoritmi pentru partiționarea graficelor nestructurate, a rețelelor și pentru calcularea ordonărilor de reducere a umplerii ale matricelor rare.
• NumPy: Pachetul fundamental pentru calculul științific cu Python.
• CGAL: algoritmi geometrici eficienți și fiabili sub forma unei biblioteci C++.
• SCOTCH: Un pachet software și biblioteci pentru partiționare secvențială și paralelă a graficelor, mapare și grupare statică, partiționare secvențială și hipergraf și ordonare secvențială și paralelă a blocurilor de matrice rare.
• MPI: Un sistem standardizat și portabil de transmitere a mesajelor conceput de un grup de cercetători din mediul academic și din industrie pentru a funcționa pe o mare varietate de computere paralele.
• VTK: Un sistem software open-source, disponibil gratuit pentru grafică 3D pe computer, procesare și vizualizare a imaginilor.
• SLEPc: O bibliotecă de software pentru rezolvarea problemelor cu valori proprii rare la scară largă pe computere paralele.

Această listă de pachete externe integrate în proiect ne oferă o idee despre capacitățile sale moștenite. De exemplu, suportul integrat pentru MPI permite scalarea între lucrătorii de la distanță într-un mediu de cluster de calcul (adică, acest cod va rula pe un super computer sau laptop).

De asemenea, este interesant de observat că există multe aplicații dincolo de calculul științific pentru care aceste proiecte ar putea fi utilizate, inclusiv modelarea financiară, procesarea imaginilor, probleme de optimizare și poate chiar jocuri video. Ar fi posibil, de exemplu, să se creeze un joc video care să folosească unii dintre acești algoritmi și tehnici open source pentru a rezolva curgerea unui fluid bidimensional, cum ar fi cea a curenților oceanici/râurilor cu care un jucător ar interacționa (poate să încerce și traversează o barcă cu debite variate de vânt și apă).

Un exemplu de aplicație: valorificarea open source pentru calculul științific

Aici voi încerca să dau o imagine a ceea ce implică dezvoltarea unui model numeric, arătând cum este dezvoltată și implementată o schemă de bază Computational Fluid Dynamics într-una dintre aceste biblioteci open source - în acest caz, proiectul FEniCS. FEnICS oferă API-uri atât în ​​Python, cât și în C++. Pentru acest exemplu, vom folosi API-ul lor Python.

Vom discuta despre un conținut mai degrabă tehnic, dar scopul va fi pur și simplu să oferim o idee despre ceea ce presupune dezvoltarea unui astfel de cod de calcul științific și cât de mult ne fac instrumentele open source de astăzi. În acest proces, sperăm că vom ajuta la demistificarea lumii complexe a calculului științific. (Rețineți că este furnizat un apendice care detaliază toate bazele matematice și științifice pentru cei care sunt interesați de acel nivel de detaliu.)

RENUNȚAREA RESPONSABILITĂȚII: Pentru acei cititori cu puține sau deloc cunoștințe în software și aplicații de calcul științific, părți din acest exemplu vă pot face să vă simțiți astfel:

Dacă da, nu dispera. Principala concluzie aici este măsura în care proiectele open source existente pot simplifica foarte mult multe dintre aceste sarcini.

Având în vedere asta, să începem prin a ne uita la demonstrația FEnICS pentru Navier-Stokes incompresibil. Această demonstrație modelează presiunea și viteza unui fluid incompresibil care curge printr-un cot în formă de L, cum ar fi o conductă sanitară.

Descrierea de pe pagina demo legată oferă o configurare excelentă și concisă a pașilor necesari pentru rularea codului și vă încurajez să aruncați o privire rapidă pentru a vedea ce este implicat. Pentru a rezuma, demonstrația va rezolva viteza și presiunea prin cot pentru ecuațiile de curgere incompresibile. Demo-ul rulează o scurtă simulare a fluidului care curge în timp, animand rezultatele pe măsură ce se desfășoară. Acest lucru se realizează prin configurarea rețelei reprezentând spațiul din țeavă și folosind metoda elementelor finite pentru a rezolva numeric viteza și presiunea în fiecare punct al rețelei. Apoi repetăm ​​în timp, actualizând câmpurile de viteză și presiune pe măsură ce mergem, folosind din nou ecuațiile pe care le avem la dispoziție.

Demo-ul funcționează bine așa cum este, dar o vom modifica ușor. Demo-ul folosește diviziunea Chorin, dar vom folosi metoda puțin diferită inspirată de Kim și Moin, care sperăm că este mai stabilă. Acest lucru ne cere doar să schimbăm ecuația folosită pentru a aproxima termenii convectivi și vâscoși, dar pentru a face acest lucru trebuie să stocăm câmpul de viteză al pasului de timp anterior și să adăugăm doi termeni suplimentari la ecuația de actualizare, care va folosi acea precedentă. informații pentru o aproximare numerică mai precisă.

Deci, să facem această schimbare. Mai întâi, adăugăm un nou obiect Function la configurare. Acesta este un obiect care reprezintă o funcție matematică abstractă, cum ar fi un vector sau un câmp scalar. Îl vom numi un1 și va stoca câmpul de viteză anterior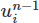 pe spațiul nostru funcțional V .

 ... # Create functions (three distinct vector fields and a scalar field) un1 = Function(V) # the previous time step's velocity field we are adding u0 = Function(V) # the current velocity field u1 = Function(V) # the next velocity field (what's being solved for) p1 = Function(Q) # the next pressure field (what's being solved for) ...

În continuare, trebuie să schimbăm modul în care „viteza provizorie” este actualizată în timpul fiecărei etape a simulării. Acest câmp reprezintă viteza aproximativă la următorul pas de timp când presiunea este ignorată (în acest moment presiunea nu este încă cunoscută). Aici înlocuim metoda divizării Chorin cu metoda pasului fracționat Kim și Moin, mai recentă. Cu alte cuvinte, vom schimba expresia pentru câmpul F1 :

A inlocui:

 # Tentative velocity field (a first prediction of what the next velocity field is) # for the Chorin style split # F1 = change in the velocity field + # convective term + # diffusive term - # body force term F1 = (1/k)*inner(u - u0, v)*dx + \ inner(grad(u0)*u0, v)*dx + \ nu*inner(grad(u), grad(v))*dx - \ inner(f, v)*dx

Cu:

 # Tentative velocity field (a first prediction of what the next velocity field is) # for the Kim and Moin style split # F1 = change in the velocity field + # convective term + # diffusive term - # body force term F1 = (1/k)*inner(u - u0, v)*dx + \ (3.0/2.0) * inner(grad(u0)*u0, v)*dx - (1.0/2.0) * inner(grad(un1)*un1, v)*dx + \ (nu/2.0)*inner(grad(u+u0), grad(v))*dx - \ inner(f, v)*dx

astfel încât demonstrația folosește acum metoda noastră actualizată pentru rezolvarea câmpului de viteză intermediară atunci când folosește F1 .

În cele din urmă, asigurați-vă că actualizăm câmpul de viteză anterior, un1 , la sfârșitul fiecărui pas de iterație

 ... # Move to next time step un1.assign(u0) # copy the current velocity field into the previous velocity field u0.assign(u1) # copy the next velocity field into the current velocity field ...

Pentru ca următorul cod să fie complet din demonstrația noastră CFD FEniCS, cu modificările noastre incluse:

 """This demo program solves the incompressible Navier-Stokes equations on an L-shaped domain using Kim and Moin's fractional step method.""" # Begin demo from dolfin import * # Print log messages only from the root process in parallel parameters["std_out_all_processes"] = False; # Load mesh from file mesh = Mesh("lshape.xml.gz") # Define function spaces (P2-P1) V = VectorFunctionSpace(mesh, "Lagrange", 2) Q = FunctionSpace(mesh, "Lagrange", 1) # Define trial and test functions u = TrialFunction(V) p = TrialFunction(Q) v = TestFunction(V) q = TestFunction(Q) # Set parameter values dt = 0.01 T = 3 nu = 0.01 # Define time-dependent pressure boundary condition p_in = Expression("sin(3.0*t)", t=0.0) # Define boundary conditions noslip = DirichletBC(V, (0, 0), "on_boundary && \ (x[0] < DOLFIN_EPS | x[1] < DOLFIN_EPS | \ (x[0] > 0.5 - DOLFIN_EPS && x[1] > 0.5 - DOLFIN_EPS))") inflow = DirichletBC(Q, p_in, "x[1] > 1.0 - DOLFIN_EPS") outflow = DirichletBC(Q, 0, "x[0] > 1.0 - DOLFIN_EPS") bcu = [noslip] bcp = [inflow, outflow] # Create functions un1 = Function(V) u0 = Function(V) u1 = Function(V) p1 = Function(Q) # Define coefficients k = Constant(dt) f = Constant((0, 0)) # Tentative velocity field (a first prediction of what the next velocity field is) # for the Kim and Moin style split # F1 = change in the velocity field + # convective term + # diffusive term - # body force term F1 = (1/k)*inner(u - u0, v)*dx + \ (3.0/2.0) * inner(grad(u0)*u0, v)*dx - (1.0/2.0) * inner(grad(un1)*un1, v)*dx + \ (nu/2.0)*inner(grad(u+u0), grad(v))*dx - \ inner(f, v)*dx a1 = lhs(F1) L1 = rhs(F1) # Pressure update a2 = inner(grad(p), grad(q))*dx L2 = -(1/k)*div(u1)*q*dx # Velocity update a3 = inner(u, v)*dx L3 = inner(u1, v)*dx - k*inner(grad(p1), v)*dx # Assemble matrices A1 = assemble(a1) A2 = assemble(a2) A3 = assemble(a3) # Use amg preconditioner if available prec = "amg" if has_krylov_solver_preconditioner("amg") else "default" # Create files for storing solution ufile = File("results/velocity.pvd") pfile = File("results/pressure.pvd") # Time-stepping t = dt while t < T + DOLFIN_EPS: # Update pressure boundary condition p_in.t = t # Compute tentative velocity step begin("Computing tentative velocity") b1 = assemble(L1) [bc.apply(A1, b1) for bc in bcu] solve(A1, u1.vector(), b1, "gmres", "default") end() # Pressure correction begin("Computing pressure correction") b2 = assemble(L2) [bc.apply(A2, b2) for bc in bcp] solve(A2, p1.vector(), b2, "cg", prec) end() # Velocity correction begin("Computing velocity correction") b3 = assemble(L3) [bc.apply(A3, b3) for bc in bcu] solve(A3, u1.vector(), b3, "gmres", "default") end() # Plot solution plot(p1, title="Pressure", rescale=True) plot(u1, title="Velocity", rescale=True) # Save to file ufile << u1 pfile << p1 # Move to next time step un1.assign(u0) u0.assign(u1) t += dt print "t =", t # Hold plot interactive()

Rularea programului arată fluxul în jurul cotului. Rulați singur codul de calcul științific pentru a-l vedea animat! Ecranele cadrului final sunt prezentate mai jos.

Presiuni relative în îndoire la sfârșitul simulării, scalate și colorate după mărime (valori nedimensionale):

Vitezele relative în curba la sfârșitul simulării ca glife vectoriale scalate și colorate după mărime (valori nedimensionale).

Deci, ceea ce am făcut a fost să luăm un demo existent, care se întâmplă să implementeze o schemă foarte asemănătoare cu a noastră destul de ușor, și am modificat-o pentru a folosi aproximări mai bune folosind informații din pasul de timp anterior.

În acest moment, s-ar putea să vă gândiți că a fost o editare banală. A fost și acesta este în mare măsură ideea. Acest proiect de calcul științific open source ne-a permis să implementăm rapid un model numeric modificat prin schimbarea a patru linii de cod. Astfel de modificări pot dura luni de zile în cazul codurilor mari de cercetare.

Proiectul are multe alte demonstrații care ar putea fi folosite ca punct de plecare. Există chiar și o serie de aplicații open source construite pe proiect care implementează diverse modele.

Concluzie

Calculul științific și aplicațiile sale sunt într-adevăr complexe. Nu se poate ocoli asta. Dar, așa cum este din ce în ce mai adevărat în atât de multe domenii, peisajul în continuă creștere al instrumentelor și proiectelor open source disponibile poate simplifica semnificativ ceea ce altfel ar fi sarcini de programare extrem de complicate și plictisitoare. Și poate că timpul este chiar aproape în care computerul științific devine suficient de accesibil pentru a fi utilizat cu ușurință dincolo de comunitatea de cercetare.

ANEXĂ: Fundamente științifice și matematice

Pentru cei interesați, aici sunt bazele tehnice ale ghidului nostru de dinamică a fluidelor computaționale de mai sus. Ceea ce urmează va servi ca un rezumat foarte util și concis al subiectelor care sunt de obicei acoperite pe parcursul a aproximativ o duzină de cursuri la nivel de absolvent. Studenții absolvenți și tipurile de matematică interesați de o înțelegere profundă a subiectului pot găsi acest material destul de captivant.

Mecanica fluidelor

„Modelarea”, în general, este procesul de rezolvare a unui sistem real cu o serie de aproximări. Modelul va implica adesea ecuații continue nepotrivite pentru implementarea computerului și, prin urmare, trebuie aproximat în continuare cu metode numerice.

Pentru mecanica fluidelor, să începem acest ghid de la ecuațiile fundamentale, ecuațiile Navier-Stokes, și să folosim asta pentru a dezvolta o schemă CFD.

Ecuațiile Navier-Stokes sunt o serie de ecuații cu diferențe parțiale (PDE) care descriu foarte bine curgerile fluidelor și sunt astfel punctul nostru de plecare. Ele pot fi derivate din legile de conservare a masei, impulsului și energiei, prezentate printr-o teoremă de transport Reynolds și aplicând teorema lui Gauss și invocând ipoteza lui Stoke. Ecuațiile necesită o ipoteză de continuu, în care se presupune că avem suficiente particule de fluid pentru a da proprietăți statistice precum temperatura, densitatea și sensul vitezei. În plus, este necesară o relație liniară între tensorul tensiunii de suprafață și tensorul vitezei de deformare, simetria în tensorul tensiunii și ipotezele fluidului izotrop. Este important să cunoaștem ipotezele pe care le facem și le moștenim în timpul acestei dezvoltări, astfel încât să putem evalua aplicabilitatea în codul rezultat. Ecuațiile Navier-Stokes în notația Einstein, fără alte prelungiri:

Conservarea masei:

Conservarea impulsului:

Conservarea Energiei:

unde stresul deviatoric este:

Deși sunt foarte generale, guvernează majoritatea fluxurilor de fluide din lumea fizică, ele nu sunt de mare folos direct. Există relativ puține soluții exacte cunoscute la ecuații, iar un premiu al mileniului de 1.000.000 de dolari este disponibil pentru oricine poate rezolva problema existenței și a netedăi. Partea importantă este că avem un punct de plecare pentru dezvoltarea modelului nostru făcând o serie de ipoteze pentru a reduce complexitatea (sunt unele dintre cele mai dificile ecuații din fizica clasică).

Pentru a menține lucrurile „simple”, vom folosi cunoștințele noastre specifice domeniului pentru a face o presupunere incompresibilă asupra fluidului și a presupune temperaturi constante, astfel încât ecuația de conservare a energiei, care devine ecuația de căldură, nu este necesară (decuplată). Acum avem două ecuații, încă PDE, dar semnificativ mai simple, rezolvând în același timp un număr mare de probleme reale de fluide.

Ecuația de continuitate

Ecuații de impuls

În acest moment avem acum un model matematic frumos pentru fluxurile de fluide incompresibile (gaze și lichide cu viteză redusă, cum ar fi apa, de exemplu). Rezolvarea manuală a acestor ecuații nu este ușoară, dar este frumos prin faptul că putem obține soluții „exacte” pentru probleme simple. Folosirea acestor ecuații pentru a rezolva probleme de interes, să spunem aerul care curge peste o aripă sau apa care curge printr-un sistem, necesită să rezolvăm aceste ecuații numeric.

Construirea unei scheme numerice

Pentru a rezolva probleme mai complexe folosind computerul, este nevoie de o metodă de rezolvare numerică a ecuațiilor noastre incompresibile. Rezolvarea numerică a ecuațiilor diferențiale parțiale sau chiar a ecuațiilor diferențiale nu este trivială. Cu toate acestea, ecuațiile noastre din acest ghid au o provocare deosebită (surpriză!). Adică, trebuie să rezolvăm ecuațiile momentului în timp ce menținem liberă divergența soluției, așa cum este cerut de continuitate. O simplă integrare în timp prin metoda Runge-Kutta este dificilă, deoarece ecuația de continuitate nu are o derivată de timp în ea.

Nu există o metodă corectă, sau chiar cea mai bună, pentru rezolvarea ecuațiilor, dar există multe opțiuni viabile. De-a lungul deceniilor, au fost găsite mai multe abordări pentru a aborda problema, cum ar fi reformularea în termeni de vorticitate și funcție de flux, introducerea compresibilității artificiale și divizarea operatorilor. Chorin (1969), apoi Kim și Moin (1984, 1990), au formulat o metodă foarte reușită și populară în trepte fracționale, care ne va permite să integrăm ecuațiile în timp ce rezolvăm câmpul de presiune direct, mai degrabă decât implicit. Metoda pasului fracționar este o metodă generală de aproximare a ecuațiilor prin împărțirea operatorilor acestora, în acest caz împărțirea în funcție de presiune. Abordarea este relativ simplă și totuși robustă, motivând alegerea sa aici.

În primul rând, trebuie să discritimăm numeric ecuațiile în timp, astfel încât să putem trece de la un moment în timp la altul. În urma lui Kim și Moin (1984), vom folosi metoda Adams-Bashforth explicită de ordinul doi pentru termenii convectivi, metoda Crank-Nicholson implicită de ordinul doi pentru termenii vâscoși, o diferență finită simplă pentru derivata timpului. , neglijând în același timp gradientul de presiune. Aceste alegeri nu sunt în niciun caz singurele aproximări care pot fi făcute: selecția lor face parte din arta construirii schemei prin controlul comportamentului numeric al schemei.

Viteza intermediară poate fi acum integrată, cu toate acestea, ignoră contribuția presiunii și este acum divergentă (incompresibilitatea necesită să fie liberă divergentă). Restul operatorului este necesar pentru a ne duce la următorul pas de timp.

Unde este un scalar pe care trebuie să îl găsim care are ca rezultat o viteză liberă divergentă. Noi putem gasi prin luarea divergenței etapei de corecție,

unde primul termen este zero așa cum este cerut de continuitate, rezultând o ecuație Poisson pentru un câmp scalar care va furniza o viteză solenoidală (liberă divergentă) la următorul pas de timp.

După cum arată Kim și Moin (1984), nu este exact presiunea ca urmare a divizării operatorului, dar poate fi găsită prin

În acest moment al tutorialului ne descurcăm destul de bine, am descris temporal ecuațiile guvernante pentru a le putea integra. Acum trebuie să discritimăm spațial operatorii. Există o serie de metode prin care am putea realiza acest lucru, de exemplu, metoda elementului finit, metoda volumului finit și metoda diferențelor finite. În lucrarea originală a lui Kim și Moin (1984), aceștia procedează cu metoda diferențelor finite. Metoda este avantajoasă pentru simplitatea sa relativă și eficiența de calcul, dar suferă din cauza geometriilor complexe, deoarece necesită o plasă structurată.

Metoda Elementelor Finite (FEM) este o selecție convenabilă pentru generalitatea sa și are câteva proiecte open source foarte frumoase care ajută la utilizarea sa. În special, se ocupă de geometrii reale în una, două și trei dimensiuni, scale pentru probleme foarte mari pe grupuri de mașini și este relativ ușor de utilizat pentru elemente de ordin înalt. De obicei, metoda este cea mai lentă dintre cele trei, cu toate acestea, ne va oferi cel mai mare kilometraj între probleme, așa că o vom folosi aici.

Chiar și atunci când implementați FEM există multe opțiuni. Aici vom folosi Galerkin FEM. Făcând acest lucru, aruncăm ecuațiile în formă reziduală ponderată înmulțind fiecare cu o funcție de test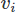 pentru vectorii și 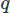pentru câmpul scalar și integrarea peste domeniu 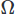. Apoi efectuăm integrarea parțială pe orice derivate de ordin înalt folosind teorema lui Stoke sau teorema divergenței. Apoi punem problema variațională, obținând schema CFD dorită.

Acum avem o schemă matematică drăguță într-o formă „convenabilă” pentru implementare, sperăm că avem o oarecare înțelegere a ceea ce era necesar pentru a ajunge acolo (multe matematică și metode de la cercetători geniali pe care le copiem și le modificăm).