Ein Leitfaden für wissenschaftliches Rechnen mit Open-Source-Tools

Historisch gesehen war Computational Science weitgehend auf den Bereich von Forschern und Doktoranden beschränkt. Im Laufe der Jahre haben wir jedoch – vielleicht ohne Wissen der größeren Software-Community – wissenschaftliche Informatik-Eierköpfe im Stillen kollaborative Open-Source-Bibliotheken kompiliert, die den Großteil der schweren Arbeit bewältigen . Das Ergebnis ist, dass es jetzt einfacher denn je ist, mathematische Modelle zu implementieren, und obwohl das Feld vielleicht noch nicht reif für den Massenkonsum ist, wurde die Messlatte für eine erfolgreiche Implementierung drastisch gesenkt. Die Entwicklung einer neuen rechnerischen Codebasis von Grund auf ist ein riesiges Unterfangen, das normalerweise in Jahren gemessen wird, aber diese wissenschaftlichen Open-Source-Computing-Projekte ermöglichen es, mit zugänglichen Beispielen zu arbeiten, um diese rechnerischen Fähigkeiten relativ schnell zu nutzen.

Da der Zweck des wissenschaftlichen Rechnens darin besteht, wissenschaftliche Einblicke in reale Systeme zu liefern, die in der Natur existieren, stellt die Disziplin die Speerspitze dar, wenn es darum geht, Computersoftware an die Realität heranzuführen. Um Software zu erstellen, die die reale Welt mit einem sehr hohen Grad an Genauigkeit und Auflösung nachahmt, muss komplexe Differentialmathematik herangezogen werden, die Wissen erfordert, das selten außerhalb der Mauern von Universitäten, nationalen Labors oder F&E-Abteilungen von Unternehmen zu finden ist. Darüber hinaus ergeben sich erhebliche numerische Herausforderungen, wenn versucht wird, das kontinuierliche, infinitesimale Gefüge der realen Welt mit der diskreten Sprache von Nullen und Einsen zu beschreiben. Ein erschöpfender Aufwand an sorgfältiger numerischer Transformation ist notwendig, um Algorithmen zu liefern, die sowohl rechnerisch handhabbar sind als auch aussagekräftige Ergebnisse liefern. Mit anderen Worten, wissenschaftliches Rechnen ist eine schwere Aufgabe.

Open-Source-Tools für wissenschaftliches Rechnen

Ich persönlich mag das FEniCS-Projekt besonders, verwende es für meine Abschlussarbeit und werde meine Voreingenommenheit bei der Auswahl dieses Projekts für unser Codebeispiel für dieses Tutorial demonstrieren. (Es gibt andere sehr hochwertige Projekte wie DUNE, die man ebenfalls verwenden könnte.)

FEniCS beschreibt sich selbst als „ein Gemeinschaftsprojekt zur Entwicklung innovativer Konzepte und Werkzeuge für automatisiertes wissenschaftliches Rechnen, mit besonderem Schwerpunkt auf der automatisierten Lösung von Differentialgleichungen durch Finite-Elemente-Methoden“. Dies ist eine leistungsstarke Bibliothek zur Lösung einer Vielzahl von Problemen und Anwendungen für wissenschaftliche Berechnungen. Zu seinen Mitwirkenden gehören das Simula Research Laboratory, die University of Cambridge, die University of Chicago, die Baylor University und das KTH Royal Institute of Technology, die es im Laufe des letzten Jahrzehnts gemeinsam zu einer unschätzbaren Ressource ausgebaut haben (siehe FEniCS Codeswarm).

Erstaunlich ist, vor wie viel Aufwand uns die FEniCS-Bibliothek bewahrt hat. Um ein Gefühl für die erstaunliche Tiefe und Breite der Themen zu bekommen, die das Projekt abdeckt, kann man sich ihr Open-Source-Lehrbuch ansehen, in dem Kapitel 21 sogar verschiedene Finite-Elemente-Schemata zur Lösung inkompressibler Strömungen vergleicht.

Hinter den Kulissen hat das Projekt für uns eine große Anzahl von Open-Source-Bibliotheken für wissenschaftliche Berechnungen integriert, die von Interesse oder direkt von Nutzen sein können. Dazu gehören, in keiner bestimmten Reihenfolge, die Projekte, die das FEniCS-Projekt ausruft:

• PETSc: Eine Suite von Datenstrukturen und Routinen für die skalierbare (parallele) Lösung wissenschaftlicher Anwendungen, die durch partielle Differentialgleichungen modelliert werden.
• Trilinos-Projekt: Eine Reihe robuster Algorithmen und Technologien zum Lösen sowohl linearer als auch nichtlinearer Gleichungen, die aus der Arbeit der Sandia National Labs entwickelt wurden.
• uBLAS: „Eine C++-Vorlagenklassenbibliothek, die BLAS Level 1, 2, 3-Funktionalität für dichte, gepackte und dünne Matrizen und viele numerische Algorithmen für lineare Algebra bereitstellt.“
• GMP: Eine kostenlose Bibliothek für Arithmetik mit beliebiger Genauigkeit, die mit vorzeichenbehafteten Ganzzahlen, rationalen Zahlen und Gleitkommazahlen arbeitet.
• UMFPACK: Eine Reihe von Routinen zum Lösen unsymmetrischer dünnbesetzter linearer Systeme, Ax=b, unter Verwendung der Unsymmetric MultiFrontal-Methode.
• ParMETIS: Eine MPI-basierte parallele Bibliothek, die eine Vielzahl von Algorithmen zum Partitionieren unstrukturierter Graphen, Netze und zum Berechnen von füllreduzierenden Ordnungen von dünn besetzten Matrizen implementiert.
• NumPy: Das grundlegende Paket für wissenschaftliches Rechnen mit Python.
• CGAL: Effiziente und zuverlässige geometrische Algorithmen in Form einer C++-Bibliothek.
• SCOTCH: Ein Softwarepaket und Bibliotheken für sequentielle und parallele Graphpartitionierung, statisches Mapping und Clustering, sequentielle Netz- und Hypergraphpartitionierung und sequentielle und parallele Sparse-Matrixblockordnung.
• MPI: Ein standardisiertes und tragbares Nachrichtenübermittlungssystem, das von einer Gruppe von Forschern aus Wissenschaft und Industrie entwickelt wurde, um auf einer Vielzahl paralleler Computer zu funktionieren.
• VTK: Ein quelloffenes, frei verfügbares Softwaresystem für 3D-Computergrafik, Bildverarbeitung und Visualisierung.
• SLEPc: Eine Softwarebibliothek zur Lösung von großskaligen dünnbesetzten Eigenwertproblemen auf Parallelrechnern.

Diese Liste externer Pakete, die in das Projekt integriert sind, gibt uns einen Eindruck von den ererbten Fähigkeiten. Die integrierte Unterstützung für MPI ermöglicht beispielsweise die Skalierung über Remote-Mitarbeiter in einer Compute-Cluster-Umgebung (dh dieser Code wird auf einem Supercomputer oder Ihrem Laptop ausgeführt).

Es ist auch interessant festzustellen, dass es viele Anwendungen jenseits des wissenschaftlichen Rechnens gibt, für die diese Projekte genutzt werden könnten, darunter Finanzmodellierung, Bildverarbeitung, Optimierungsprobleme und vielleicht sogar Videospiele. Es wäre zum Beispiel möglich, ein Videospiel zu erstellen, das einige dieser Open-Source-Algorithmen und -Techniken verwendet, um nach einer zweidimensionalen Flüssigkeitsströmung zu suchen, wie z Segeln Sie mit einem Boot bei unterschiedlichen Wind- und Wasserströmungen).

Eine Beispielanwendung: Nutzung von Open Source für wissenschaftliches Rechnen

Hier werde ich versuchen, einen Vorgeschmack darauf zu geben, was die Entwicklung eines numerischen Modells beinhaltet, indem ich zeige, wie ein grundlegendes Computational Fluid Dynamics-Schema entwickelt und in einer dieser Open-Source-Bibliotheken implementiert wird - in diesem Fall dem FEniCS-Projekt. FEnICS bietet APIs sowohl in Python als auch in C++. Für dieses Beispiel verwenden wir ihre Python-API.

Wir werden einige eher technische Inhalte diskutieren, aber das Ziel wird einfach sein, einen Vorgeschmack darauf zu geben, was die Entwicklung eines solchen wissenschaftlichen Computercodes mit sich bringt und wie viel Kleinarbeit die heutigen Open-Source-Tools für uns erledigen. Dabei werden wir hoffentlich dazu beitragen, die komplexe Welt des wissenschaftlichen Rechnens zu entmystifizieren. (Beachten Sie, dass ein Anhang bereitgestellt wird, der alle mathematischen und wissenschaftlichen Grundlagen für diejenigen enthält, die an dieser Detailebene interessiert sind.)

HAFTUNGSAUSSCHLUSS: Für diejenigen Leser mit wenig oder keinem Hintergrundwissen in Software und Anwendungen für wissenschaftliche Berechnungen könnten Teile dieses Beispiels Ihnen folgendes Gefühl vermitteln:

Wenn ja, verzweifeln Sie nicht. Die wichtigste Erkenntnis hier ist das Ausmaß, in dem bestehende Open-Source-Projekte viele dieser Aufgaben erheblich vereinfachen können.

Sehen wir uns vor diesem Hintergrund zunächst die FEnICS-Demo für inkomprimierbare Navier-Stokes an. Diese Demo modelliert den Druck und die Geschwindigkeit einer inkompressiblen Flüssigkeit, die durch eine L-förmige Biegung fließt, z. B. ein Sanitärrohr.

Die Beschreibung auf der verlinkten Demo-Seite bietet eine ausgezeichnete, prägnante Einrichtung der notwendigen Schritte zum Ausführen des Codes, und ich ermutige Sie, einen kurzen Blick darauf zu werfen, um zu sehen, was dazu gehört. Zusammenfassend wird die Demo die Geschwindigkeit und den Druck durch die Biegung für die inkompressiblen Strömungsgleichungen lösen. Die Demo führt eine kurze Simulation des Flüssigkeitsflusses im Laufe der Zeit durch und animiert die Ergebnisse während des Ablaufs. Dies wird erreicht, indem das Netz eingerichtet wird, das den Raum im Rohr darstellt, und die Finite-Elemente-Methode verwendet wird, um die Geschwindigkeit und den Druck an jedem Punkt des Netzes numerisch zu lösen. Wir iterieren dann durch die Zeit und aktualisieren dabei die Geschwindigkeits- und Druckfelder, wobei wir wiederum die uns zur Verfügung stehenden Gleichungen verwenden.

Die Demo funktioniert gut, wie sie ist, aber wir werden sie leicht modifizieren. Die Demo verwendet den Chorin-Split, aber wir werden stattdessen die etwas andere, von Kim und Moin inspirierte Methode verwenden, von der wir hoffen, dass sie stabiler ist. Dazu müssen wir nur die Gleichung ändern, die verwendet wird, um die konvektiven und viskosen Terme zu approximieren, aber dazu müssen wir das Geschwindigkeitsfeld des vorherigen Zeitschritts speichern und zwei zusätzliche Terme zur Aktualisierungsgleichung hinzufügen, die diesen vorherigen verwenden Informationen für eine genauere numerische Annäherung.

Nehmen wir also diese Änderung vor. Zuerst fügen wir dem Setup ein neues Function Objekt hinzu. Dies ist ein Objekt, das eine abstrakte mathematische Funktion wie ein Vektor- oder Skalarfeld darstellt. Wir nennen es un1 , es speichert das vorherige Velocity-Feld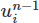 auf unserem Funktionsraum V .

 ... # Create functions (three distinct vector fields and a scalar field) un1 = Function(V) # the previous time step's velocity field we are adding u0 = Function(V) # the current velocity field u1 = Function(V) # the next velocity field (what's being solved for) p1 = Function(Q) # the next pressure field (what's being solved for) ...

Als Nächstes müssen wir die Art und Weise ändern, wie die „vorläufige Geschwindigkeit“ in jedem Schritt der Simulation aktualisiert wird. Dieses Feld stellt die ungefähre Geschwindigkeit beim nächsten Zeitschritt dar, wenn der Druck ignoriert wird (zu diesem Zeitpunkt ist der Druck noch nicht bekannt). Hier ersetzen wir die Chorin-Split-Methode durch die neuere Kim-und-Moin-Bruchschrittmethode. Mit anderen Worten, wir ändern den Ausdruck für das Feld F1 :

Ersetzen:

 # Tentative velocity field (a first prediction of what the next velocity field is) # for the Chorin style split # F1 = change in the velocity field + # convective term + # diffusive term - # body force term F1 = (1/k)*inner(u - u0, v)*dx + \ inner(grad(u0)*u0, v)*dx + \ nu*inner(grad(u), grad(v))*dx - \ inner(f, v)*dx

Mit:

 # Tentative velocity field (a first prediction of what the next velocity field is) # for the Kim and Moin style split # F1 = change in the velocity field + # convective term + # diffusive term - # body force term F1 = (1/k)*inner(u - u0, v)*dx + \ (3.0/2.0) * inner(grad(u0)*u0, v)*dx - (1.0/2.0) * inner(grad(un1)*un1, v)*dx + \ (nu/2.0)*inner(grad(u+u0), grad(v))*dx - \ inner(f, v)*dx

sodass die Demo jetzt unsere aktualisierte Methode zum Lösen des Zwischengeschwindigkeitsfelds verwendet, wenn sie F1 verwendet.

Stellen Sie schließlich sicher, dass wir das vorherige Geschwindigkeitsfeld un1 am Ende jedes Iterationsschritts aktualisieren

 ... # Move to next time step un1.assign(u0) # copy the current velocity field into the previous velocity field u0.assign(u1) # copy the next velocity field into the current velocity field ...

Das Folgende ist also der vollständige Code aus unserer FEniCS CFD-Demo, einschließlich unserer Änderungen:

 """This demo program solves the incompressible Navier-Stokes equations on an L-shaped domain using Kim and Moin's fractional step method.""" # Begin demo from dolfin import * # Print log messages only from the root process in parallel parameters["std_out_all_processes"] = False; # Load mesh from file mesh = Mesh("lshape.xml.gz") # Define function spaces (P2-P1) V = VectorFunctionSpace(mesh, "Lagrange", 2) Q = FunctionSpace(mesh, "Lagrange", 1) # Define trial and test functions u = TrialFunction(V) p = TrialFunction(Q) v = TestFunction(V) q = TestFunction(Q) # Set parameter values dt = 0.01 T = 3 nu = 0.01 # Define time-dependent pressure boundary condition p_in = Expression("sin(3.0*t)", t=0.0) # Define boundary conditions noslip = DirichletBC(V, (0, 0), "on_boundary && \ (x[0] < DOLFIN_EPS | x[1] < DOLFIN_EPS | \ (x[0] > 0.5 - DOLFIN_EPS && x[1] > 0.5 - DOLFIN_EPS))") inflow = DirichletBC(Q, p_in, "x[1] > 1.0 - DOLFIN_EPS") outflow = DirichletBC(Q, 0, "x[0] > 1.0 - DOLFIN_EPS") bcu = [noslip] bcp = [inflow, outflow] # Create functions un1 = Function(V) u0 = Function(V) u1 = Function(V) p1 = Function(Q) # Define coefficients k = Constant(dt) f = Constant((0, 0)) # Tentative velocity field (a first prediction of what the next velocity field is) # for the Kim and Moin style split # F1 = change in the velocity field + # convective term + # diffusive term - # body force term F1 = (1/k)*inner(u - u0, v)*dx + \ (3.0/2.0) * inner(grad(u0)*u0, v)*dx - (1.0/2.0) * inner(grad(un1)*un1, v)*dx + \ (nu/2.0)*inner(grad(u+u0), grad(v))*dx - \ inner(f, v)*dx a1 = lhs(F1) L1 = rhs(F1) # Pressure update a2 = inner(grad(p), grad(q))*dx L2 = -(1/k)*div(u1)*q*dx # Velocity update a3 = inner(u, v)*dx L3 = inner(u1, v)*dx - k*inner(grad(p1), v)*dx # Assemble matrices A1 = assemble(a1) A2 = assemble(a2) A3 = assemble(a3) # Use amg preconditioner if available prec = "amg" if has_krylov_solver_preconditioner("amg") else "default" # Create files for storing solution ufile = File("results/velocity.pvd") pfile = File("results/pressure.pvd") # Time-stepping t = dt while t < T + DOLFIN_EPS: # Update pressure boundary condition p_in.t = t # Compute tentative velocity step begin("Computing tentative velocity") b1 = assemble(L1) [bc.apply(A1, b1) for bc in bcu] solve(A1, u1.vector(), b1, "gmres", "default") end() # Pressure correction begin("Computing pressure correction") b2 = assemble(L2) [bc.apply(A2, b2) for bc in bcp] solve(A2, p1.vector(), b2, "cg", prec) end() # Velocity correction begin("Computing velocity correction") b3 = assemble(L3) [bc.apply(A3, b3) for bc in bcu] solve(A3, u1.vector(), b3, "gmres", "default") end() # Plot solution plot(p1, title="Pressure", rescale=True) plot(u1, title="Velocity", rescale=True) # Save to file ufile << u1 pfile << p1 # Move to next time step un1.assign(u0) u0.assign(u1) t += dt print "t =", t # Hold plot interactive()

Das Ausführen des Programms zeigt den Fluss um den Ellbogen herum. Führen Sie den wissenschaftlichen Rechencode selbst aus, um ihn animiert zu sehen! Bildschirme des letzten Frames sind unten dargestellt.

Relativdrücke im Bogen am Ende der Simulation, skaliert und betragsmäßig eingefärbt (dimensionslose Werte):

Relativgeschwindigkeiten in der Biegung am Ende der Simulation als betragsmäßig skalierte und eingefärbte Vektorglyphen (dimensionslose Werte).

Wir haben also eine vorhandene Demo genommen, die ein Schema, das unserem sehr ähnlich ist, ziemlich einfach implementiert, und es modifiziert, um bessere Annäherungen zu verwenden, indem wir Informationen aus dem vorherigen Zeitschritt verwenden.

An dieser Stelle denken Sie vielleicht, dass dies eine triviale Bearbeitung war. Es war, und das ist im Wesentlichen der Punkt. Dieses wissenschaftliche Open-Source-Computing-Projekt hat es uns ermöglicht, ein modifiziertes numerisches Modell schnell zu implementieren, indem wir vier Codezeilen geändert haben. Solche Änderungen können in großen Forschungscodes Monate dauern.

Das Projekt hat viele andere Demos, die als Ausgangspunkt verwendet werden könnten. Es gibt sogar eine Reihe von Open-Source-Anwendungen, die auf dem Projekt aufbauen und verschiedene Modelle implementieren.

Fazit

Wissenschaftliches Rechnen und seine Anwendungen sind in der Tat komplex. Daran führt kein Weg vorbei. Aber wie es in so vielen Bereichen zunehmend zutrifft, kann die ständig wachsende Landschaft verfügbarer Open-Source-Tools und -Projekte das, was ansonsten äußerst komplizierte und langwierige Programmieraufgaben wären, erheblich vereinfachen. Und vielleicht ist sogar die Zeit nahe, in der das wissenschaftliche Rechnen so zugänglich wird, dass es bereitwillig über die Forschungsgemeinschaft hinaus genutzt wird.

ANHANG: Wissenschaftliche und mathematische Grundlagen

Für Interessierte finden Sie hier die technischen Grundlagen unseres Leitfadens zur Computational Fluid Dynamics oben. Das Folgende dient als sehr nützliche und prägnante Zusammenfassung von Themen, die normalerweise im Laufe von etwa einem Dutzend Graduiertenkursen behandelt werden. Doktoranden und Mathematiker, die an einem tieferen Verständnis des Themas interessiert sind, werden dieses Material möglicherweise sehr ansprechend finden.

Strömungsmechanik

„Modellierung“ ist im Allgemeinen der Prozess der Lösung eines realen Systems mit einer Reihe von Annäherungen. Das Modell beinhaltet häufig kontinuierliche Gleichungen, die für eine Computerimplementierung schlecht geeignet sind, und muss daher mit numerischen Verfahren weiter angenähert werden.

Für die Strömungsmechanik beginnen wir diesen Leitfaden mit den Grundgleichungen, den Navier-Stokes-Gleichungen, und verwenden diese, um ein CFD-Schema zu entwickeln.

Die Navier-Stokes-Gleichungen sind eine Reihe partieller Differentialgleichungen (PDEs), die Fluidströmungen sehr gut beschreiben und somit unser Ausgangspunkt sind. Sie können aus Massen-, Impuls- und Energieerhaltungsgesetzen abgeleitet werden, die durch ein Reynolds-Transporttheorem geworfen werden und das Gaußsche Theorem anwenden und die Stoke-Hypothese aufrufen. Die Gleichungen erfordern eine Kontinuumsannahme, bei der angenommen wird, dass wir genügend Fluidpartikel haben, um statistischen Eigenschaften wie Temperatur, Dichte und Geschwindigkeit Bedeutung zu geben. Zusätzlich werden eine lineare Beziehung zwischen dem Oberflächenspannungstensor und dem Dehnungsratentensor, eine Symmetrie im Spannungstensor und Annahmen über isotrope Fluide benötigt. Es ist wichtig, die Annahmen zu kennen, die wir während dieser Entwicklung treffen und übernehmen, damit wir die Anwendbarkeit im resultierenden Code bewerten können. Die Navier-Stokes-Gleichungen in Einstein-Notation, ohne weiteres:

Erhaltung der Masse:

Impulserhaltung:

Energieerhaltung:

wo die deviatorische Spannung ist:

Obwohl sie sehr allgemein sind und die meisten Flüssigkeitsströme in der physischen Welt regeln, sind sie direkt nicht von großem Nutzen. Es gibt relativ wenige bekannte exakte Lösungen für die Gleichungen, und ein Millennium-Preis in Höhe von 1.000.000 US-Dollar ist für jeden da draußen, der das Problem der Existenz und Glätte lösen kann. Der wichtige Teil ist, dass wir einen Ausgangspunkt für die Entwicklung unseres Modells haben, indem wir eine Reihe von Annahmen treffen, um die Komplexität zu reduzieren (sie sind einige der schwierigsten Gleichungen in der klassischen Physik).

Um die Dinge „einfach“ zu halten, verwenden wir unser domänenspezifisches Wissen, um eine inkompressible Annahme für das Fluid zu treffen und konstante Temperaturen anzunehmen, so dass die Energieerhaltungsgleichung, die zur Wärmegleichung wird, nicht benötigt wird (entkoppelt). Wir haben jetzt zwei Gleichungen, immer noch PDEs, aber wesentlich einfacher, während sie immer noch eine große Anzahl echter Flüssigkeitsprobleme lösen.

Kontinuitätsgleichung

Impulsgleichungen

An dieser Stelle haben wir nun ein nettes mathematisches Modell für inkompressible Flüssigkeitsströmungen (z. B. Gase und Flüssigkeiten mit niedriger Geschwindigkeit wie Wasser). Diese Gleichungen direkt von Hand zu lösen ist nicht einfach, aber es ist schön, dass wir „exakte“ Lösungen für einfache Probleme erhalten können. Um diese Gleichungen zu verwenden, um Probleme von Interesse zu lösen, z. B. Luft, die über einen Flügel strömt, oder Wasser, das durch ein System fließt, müssen wir diese Gleichungen numerisch lösen.

Erstellen eines numerischen Schemas

Um komplexere Probleme mit dem Computer zu lösen, wird eine Methode zur numerischen Lösung unserer inkompressiblen Gleichungen benötigt. Partielle Differentialgleichungen oder sogar Differentialgleichungen numerisch zu lösen ist nicht trivial. Unsere Gleichungen in diesem Leitfaden haben jedoch eine besondere Herausforderung (Überraschung!). Das heißt, wir müssen die Impulsgleichungen lösen und dabei die Lösung divergenzfrei halten, wie es die Kontinuität erfordert. Eine einfache Zeitintegration durch so etwas wie das Runge-Kutta-Verfahren wird erschwert, da die Kontinuitätsgleichung keine Zeitableitung enthält.

Es gibt keine richtige oder gar beste Methode zum Lösen der Gleichungen, aber es gibt viele praktikable Optionen. Im Laufe der Jahrzehnte wurden verschiedene Ansätze gefunden, um das Problem anzugehen, wie z. B. die Neuformulierung in Bezug auf die Vorticity und die Stromfunktion, die Einführung künstlicher Kompressibilität und Operator-Splitting. Chorin (1969) und dann Kim und Moin (1984, 1990) formulierten eine sehr erfolgreiche und beliebte Bruchschrittmethode, die es uns ermöglicht, die Gleichungen zu integrieren, während wir direkt und nicht implizit nach dem Druckfeld lösen. Die Bruchschrittmethode ist eine allgemeine Methode zur Annäherung von Gleichungen durch Aufspalten ihrer Operatoren, in diesem Fall Aufspalten entlang des Drucks. Der Ansatz ist relativ einfach und dennoch robust, was seine Wahl hier motiviert.

Zuerst müssen wir die Gleichungen zeitlich numerisch diskritisieren, damit wir von einem Zeitpunkt zum nächsten schreiten können. In Anlehnung an Kim und Moin (1984) verwenden wir die explizite Adams-Bashforth-Methode zweiter Ordnung für die konvektiven Terme, die implizite Crank-Nicholson-Methode zweiter Ordnung für die viskosen Terme, eine einfache endliche Differenz für die Zeitableitung , unter Vernachlässigung des Druckgradienten. Diese Auswahlmöglichkeiten sind keineswegs die einzigen Annäherungen, die gemacht werden können: Ihre Auswahl ist Teil der Kunst beim Erstellen des Schemas durch Steuern des numerischen Verhaltens des Schemas.

Die Zwischengeschwindigkeit kann jetzt integriert werden, ignoriert jedoch den Beitrag des Drucks und ist jetzt divergent (Inkompressibilität erfordert, dass sie divergent frei ist). Der Rest des Operators wird benötigt, um uns zum nächsten Zeitschritt zu bringen.

wo ist ein Skalar, den wir finden müssen, der zu einer divergierenden freien Geschwindigkeit führt. Wir können finden indem man die Divergenz des Korrekturschritts nimmt,

wobei der erste Term Null ist, wie es die Kontinuität erfordert, was eine Poisson-Gleichung für ein Skalarfeld ergibt, die im nächsten Zeitschritt eine Solenoid- (divergente freie) Geschwindigkeit liefert.

Wie Kim und Moin (1984) zeigen, ist nicht genau der Druck als Ergebnis der Operatoraufteilung, kann aber durch gefunden werden

An diesem Punkt im Tutorial sind wir ziemlich gut, wir haben die maßgeblichen Gleichungen zeitlich diskritisiert, damit wir sie integrieren können. Wir müssen nun die Operatoren räumlich diskriminieren. Es gibt eine Reihe von Methoden, mit denen wir dies erreichen könnten, zum Beispiel die Finite-Elemente-Methode, die Finite-Volumen-Methode und die Finite-Differenzen-Methode. In der Originalarbeit von Kim und Moin (1984) gehen sie mit der Finite-Differenzen-Methode vor. Das Verfahren ist wegen seiner relativen Einfachheit und Recheneffizienz vorteilhaft, leidet jedoch bei komplexen Geometrien, da es ein strukturiertes Netz erfordert.

Die Finite-Elemente-Methode (FEM) ist aufgrund ihrer Allgemeingültigkeit eine bequeme Wahl und hat einige sehr schöne Open-Source-Projekte, die bei ihrer Verwendung helfen. Insbesondere handhabt es reale Geometrien in ein-, zwei- und dreidimensionalen Dimensionen, skaliert für sehr große Probleme auf Maschinenclustern und ist relativ einfach für Elemente hoher Ordnung zu verwenden. Typischerweise ist die Methode die langsamere der drei, aber sie wird uns bei Problemen am meisten helfen, also werden wir sie hier verwenden.

Auch bei der Umsetzung der FEM gibt es viele Möglichkeiten. Hier verwenden wir die Galerkin FEM. Dabei gießen wir die Gleichungen in gewichtete Residuenform, indem wir sie jeweils mit einer Testfunktion multiplizieren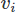 für die Vektoren und 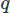für das skalare Feld und Integrieren über die Domäne 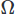. Wir führen dann eine partielle Integration an beliebigen Ableitungen hoher Ordnung unter Verwendung des Stoke-Theorems oder des Divergenz-Theorems durch. Wir stellen dann das Variationsproblem, was unser gewünschtes CFD-Schema ergibt.

Wir haben jetzt ein nettes mathematisches Schema in einer „bequemen“ Form für die Implementierung, hoffentlich mit einem gewissen Gefühl dafür, was nötig war, um dorthin zu gelangen (viel Mathematik und Methoden von brillanten Forschern, die wir ziemlich kopieren und optimieren).